可逆热机有个重要的函数，克劳修斯命名为熵(entropy)S。

一代天骄波尔兹曼（Boltzmann）与统计物理（3）

已有 2163 次阅读 2013-7-24 04:29 |个人分类:科学史故事|系统分类:科普集锦|关键词:统计

上两篇博文絮絮叨叨谈了第二定律发现过程的前三步。下面要说第四步。本来呢，按不才的风格，一页纸把四大步都说尽，岂不痛快。不料又有红颜知己说你历来心高气傲，说什么事不点到即止，一副“那还用说？”的臭架子。那就啰嗦一点吧。其实这四步推演，都可分别在不同的地方或书中找到。本人将其制成羊肉串，不仅仅为了吃着香，是让人别忘了第二定律多么简单明了，而其妊娠诞生多么艰难，给工业界带来多少福祉，给科学界带来多少美梦与噩魇，那一个名词“熵”，便把物理界搞得神魂颠倒，天下大乱，群雄遍野。几世几劫过去，至今仍不见大治。君不见There are as many viewpoints as physicists in statistical mechanics.忘了谁说的。
话说十九世纪中叶，力学及热力学界国际基本格局是德英法鼎足而立。应该是当年莱布尼兹、牛顿和笛卡尔三个王者英姿勃发三分力学天下的遗产。君不见这阵容，南有法兰西卡诺、科拉贝红（Clapeyron）、及后来的彭佳来（Poincaré）等，西有英伦哈密屯（Hamilton）、汤姆孙、焦耳及后来的麦克斯韦（Maxwell）等，北有日耳曼克劳修斯（Clausius）、赫兹（Hertz）、海姆火滋（Helmholtz）及后来的波尔兹曼等。
单说这克劳修斯，格物之功了得，对着天使热机，务要即物穷理，十几年如一日。熬到1865年，成了正果，终于把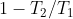背后的‘理’穷尽，大白于天下。说来令人吃醋而嘡目，没什么神秘的，不过脑筋急转弯，半分钟推算完毕。设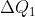为高温热源给热机的热量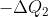，为低温热源给热机的热量。那么根据定义，热机转一圈回到原地，效率就是。　
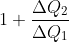如果是卡诺可逆热机，如汤姆孙所说，此效率必等于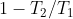。立马写出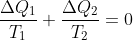。这个公式可写成热机转一圈吸收N次热量，每个热量被当时的温度除，都加起来等于零。意思是可逆热机有个重要的函数，他命名为熵(entropy)S。其变化就是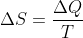。转一圈变化为零说明它是位置（状态）函数，跟路径无关。这位乱世奸雄就此诞生。且慢，这只是第二定律的一个面目。
如果是不可逆热机，此效率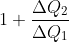必小于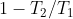（小卡诺说的），立刻写出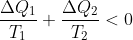。与可逆热机的熵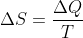及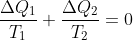比较一下， 立刻可以写出。
这就是克劳修斯完成的第四步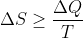，也称为克劳修斯不等式，即后来的热力学第二定律。本人生在当时就好了。
诸位读过这三篇博文，不知有何感想。我的一个感想是，其理、其逻辑、其推演如此简单明了，想违反它是不可能的。除非永动机再世。如果你自己定义一个“熵”，如上文的三个例子，那是另一回事，与克劳修斯的熵沾不上亲戚。没必要用热力学第二定律的英名做广告。
但这些博文的目的不在于第二定律本身。而是说说波尔兹曼大闹天宫的历史背景。当时及后来对熵的理解是，它代表运动状态的混乱程度。物质是由小粒子构成的力学系统。那这力学运动的混乱度为什么只升不落（对孤立体系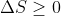）？二十几岁的波尔兹曼，初生牛犊，就有一个梦想：第二定律是力学体系的行为，只能用牛顿力学解释。哪成想，这一下捅了天大的娄子。。。