somephysics 曾博BBOC 角动量不为0的波函数，在空间存在极化。 即便没有外加光子的骚扰，因为真空震荡，这些真空中的虚光子也可以诱导电子衰变，形成自发辐射

即便没有外加光子的骚扰，因为真空震荡，这些真空中的虚光子也可以诱导电子衰变，形成自发辐射

3. 电子的干涉：

如果没有外界扰动，电子将永远地在自己地能级上呆下去，他们的确并不会干涉。然而在外加电磁波存在的情况下，局面就发生了改变。

由微扰理论我们可知，系统在存在扰动情况下的本征态，将不可避免地成为无微扰时本征态的线性组合，也就是相干态

http://zhan.renren.com/somephysics?from=template


http://zhan.renren.com/profile/223331581


曾博BBOC

原子跃迁的秘密

主说：让原子跃迁

于是

原子见到光，便会了跃迁

 

原子中每个电子原本都存在于各自稳定的能级之中，因此原子自身是稳定的。假使有一束光子袭来，实验告诉我们，电子能够一份一份地吸收这些光子，且自身从低能级跃迁到高能级上去。与此同时，激光告诉我们，电子也能被这个光子诱导，从一个高能级衰变到低能级下来；此外，led灯也告诉我们，即便没有外加光子的骚扰，因为真空震荡，这些真空中的虚光子也可以诱导电子衰变，形成自发辐射。电子和光子的相互作用，不可谓不丰富，不可谓不独特，不可谓不神奇。

然而电子－光子相互作用的跃迁是要满足一定条件的。从能量上看，能量要守恒：Ei=Ef+gamma。其中Ef是终态电子在原子核中的能量，Ei是初态的能量，gamma是光子的能量。除此之外，角动量也要守恒：电子的初态绕着原子核转，有这么一个角动量a，终态上，电子以另外一种形态绕着原子核转，有这么一个角动量b。这两个角动量的差必须由光子来补充，这就是角动量守恒的限制。

不过一个以概率云存在的电子，是通过何种机制辐射和吸收光子的呢？那么电子波函数的跃迁和一个经典的辐射模型有没有什么联系？从经典的电磁理论中我们且知，一个变速运动的电子能发出光子；一个简谐震荡的偶极子也能够发射光子（偶极子辐射）。这两者之间是否存在着联系？本文希望能在有限的篇幅内理其深意，予以解答。

 杨氏的量 | 只看Ta

是不是想问为什么角动量的转轴是对称轴才成立？
我想是因为L=Iω中，转动惯量I需必须满足平行轴定理
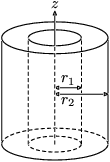
这是维基百科中给的图例，其中正在转动的圆球是一个质点，当质点转动时，我们在计算转动惯量I时不需要计算转轴的位置

但是，当转动物体是一个多质点组成的系统时（比如一个圆盘或者圆柱），转动惯量，我们就要用积分计算转动惯量，为了便于计算，在计算常用的转动惯量时，可以参照转动惯量列表
也就是说，如果定义中不规定转轴不是对称轴的话，我们就无法计算积分

[0] |

2楼

2013-03-19 16:58 Mannose (楼主) | 只看Ta

引用@杨氏的量 的话：是不是想问为什么角动量的转轴是对称轴才成立？我想是因为L=Iω中，转动惯量I需必须满足平行轴定理这是维基百科中给的图例，其中正在转动的圆球是一个质点，当质点转动时，我们在计算转动惯量I时不需要计算转轴的位置但是，当转动物体是一个多质点组成的系统时（比如一个圆盘或者圆柱），转动惯量，我们就要用积分计算转动惯量，为了便于计算，在计算常用的转动惯量时，可以参照也就是说，如果定义中不规定转轴不是对称轴的话，我们就无法计算积分

是说当转动轴不是对称轴的时候，用积分就没办法算转动惯量了吗？

[0] |

3楼

2013-03-19 17:15 杨氏的量 | 只看Ta

引用@Mannose 的话：是说当转动轴不是对称轴的时候，用积分就没办法算转动惯量了吗？

对的，计算还原到微积分中，你会发现，如同这样的刚体：

Z轴必须在对称轴才能计算

[0] |

4楼

2013-03-19 18:42 Mannose (楼主) | 只看Ta

引用@杨氏的量 的话：对的，计算还原到微积分中，你会发现，如同这样的刚体：Z轴必须在对称轴才能计算

谢谢

[0] |

5楼

2013-03-22 11:46 蜡笔桶装鬼小戏 物理专业 | 只看Ta

一般情况下的L=Iω是个矢量方程，其中的I是一个二阶张量……
在转轴为对称轴的情况下可以退化为对应的标量方程，否则会有一些烦死人的交叉项……

1. 稳态的波函数：

作为准备，我们以氢原子为例，将电子在稳态下各个能级的波函数绘出如下：