Curvature: Definition, Derivation
高斯在1827年发现这两个曲率的乘积具有惊人的属性。当我们令曲面在空间变型,只要它没有拉长缩短,这个积是不变的!后世称这个积为高斯曲率。
高斯在1827年发现这两个曲率的乘积具有惊人的属性。当我们令曲面在空间变型,只要它没有拉长缩短,这个积是不变的!后世称这个积为高斯曲率。
曲率曲率说明
表示曲线弯曲程度的量.
平面曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。曲率越大,表示曲线的弯曲程度越大。
K=lim|Δα/Δs|,Δs趋向于0的时候,定义K就是曲率。
曲率的倒数就是曲率半径。
圆弧的曲率半径,就是以这段圆弧为一个圆的一部分时,所成的圆的半径。 曲率半径越大,圆弧越平缓,曲率半径越小,圆弧越陡。曲率半径的倒数就是曲率。曲率 k = (转过的角度/对应的弧长)。当 角度和弧长同时趋近于0时,就是关于任意形状的光滑曲线的曲率的标准定义。而对于圆,曲率不随位置变化。
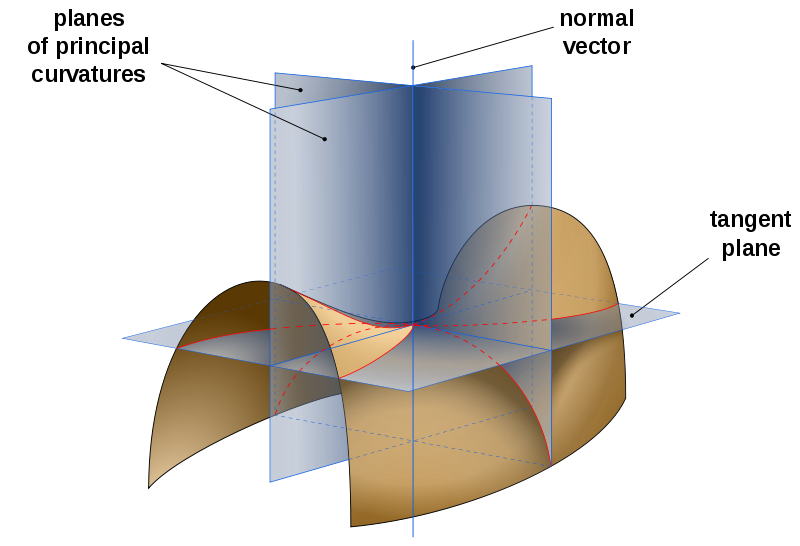
高斯曲率 曲面论中最重要的内蕴几何量。设曲 面在P点处 的两个主曲率为k1,k2,它们的乘积k=k1·k2称为曲面 于该点的总曲率或高斯曲率。它反映了曲面的一股弯曲程度。高斯曲率k的绝对值有明显的几何意义。设Δб是曲面上包含P点的一小片曲面(其面积仍用Δб表示),把Δб上的每点的单位法向量n平移到E3的原点O处,那么n的终点 的轨迹是 以O为中心的单位球面 S2上的一块区域 Δб* 。这个对应称为高斯映射。曲面在P点邻近弯曲程度可用Δб*( 其面积仍用Δб*表示)与Δб的面积比刻画。曲面在P点的 高斯曲率的 绝对值正是这个比值当Δб收缩成P点时的极限。
故事:
古典的几何学者在讨论三维空间中的曲面时,他们留意到曲面上每一点的曲率,都有两个不同的选择。比如在一个圆柱面上,一个方向是沿其横切的圆,另一个则是沿垂直线。
高斯在1827年发现这两个曲率的乘积具有惊人的属性。当我们令曲面在空间变型,只要它没有拉长缩短,这个积是不变的!后世称这个积为高斯曲率。
内蕴几何
高斯把这条定理写入《曲面通论》一书中。他指出必须把曲面的内在性质,即身处曲面内扁小甲虫所经验的属性,与其外在的,即依赖于曲面如何置于空间的性质区分开来,而只有内在性质,才值得“几何学家焚膏继晷,兀兀穷年地上下求索”。后世称研究这些性质的学问为内蕴几何。
https://www.youtube.com/watch?v=N4ZdUKe6_HQ
高斯曲率决定曲面的内蕴几何
从球面剪取一片曲面,其高斯曲率为正常数。反过来说,局部而言,任何具正常曲率的曲面都可以等距地映射成球面的一部分。
类似地,从双曲曲面剪取的一片,其高斯曲率恒等于―1,而反过来说曲率等于―1的曲面与双面曲面局部相等。双曲曲面曾在讨论欧氏第五公理时论及。
高斯对几何的深思
高斯显然因他的定理兴奋不已。但他并没有认为人们对空间已认识透彻。
高斯:“我愈来愈相信,人类的理性并不能证明或理解几何的必要性。也许后世能对空间的本质有新的洞见,但目前这却是不可能的事。”
定义:
曲面论中最重要的内蕴几何量。设曲 面在P点处的两个主曲率为k1,k2,它们的乘积k=k1·k2称为曲面于该点的总曲率或高斯曲率。它反映了曲面的一股弯曲程度。高斯曲率k的绝对值有明显的几何意义。设Δб是曲面上包含P点的一小片曲面(其面积仍用Δб表示),把Δб上的每点的单位法向量n平移到E3的原点O处,那么n的终点的轨迹是以O为中心的单位球面 S2上的一块区域 Δб* 。这个对应称为高斯映射。曲面在P点邻近弯曲程度可用Δб*( 其面积仍用Δб*表示)与Δб的面积比刻画。曲面在P点的 高斯曲率的 绝对值正是这个比值当Δб收缩成P点时的极限。亦即
高斯曲率的符号则指明曲面弯曲的朝向
《数理同源2》-广义相对论与黎曼几何-1
|||
第二篇黎曼几何和广义相对论
1. 既古老又现代的几何学
几何是一门古老的学科。恐怕没有哪一门学科,像欧几里德几何学那样,在公元前就已经被创立成形,历经2000多年,至今还活跃在许多课堂上和数学竞赛试题中。尽管目前中国的中学教育已经不把平面几何当作必修课,一些学校删减了许多内容或者干脆取消了该门课程,但在上世纪的60-80年代,中国学生平面几何的水平肯定是算世界上比较高的。笔者还清楚地记得,解决平面几何难题,是本人中学时代的最爱。我们高中的数学老师兼班主任,是一个刚从师范毕业的年轻人,对数学教学充满热情。印象颇深的是他在黑板上画圆的绝活,他手握粉笔一挥一就,一笔下来,立刻在黑板上出现了一个规整的圆圈,用目测法很难看出这不是圆规画出来的。在他的影响下,我们班一半人都变成了数学迷,几何迷,大家在几何世界中遨游,从中体会到数学的奥妙,也感受到无限的乐趣。那两年,在教室的黑板上、课桌上,室外的石头边、树墩上,操场的篮球架上,随处可见同学们为思考几何题而画出来的三角形、直线、和圆圈。也许总体而言,中国式的教育方法忽略了发展学生改革创新的能力,但我深信,那个时代我们解决思考的无数道数学几何难题,对训练空间想象能力、逻辑推理能力,起了非常重要的作用。
纵观科学史,牛顿、爱因斯坦都是伟人,欧拉、高斯……伟大的数学家也可以列出不少,但恐怕很难找出像欧几里德这样的科学家,从2000多年前一直到现代,人们还经常提到以他命名的”欧几里德空间”、”欧几里德几何”等等名词,真可谓名垂千古而不朽了。阿基米德可能也能算一个,牛顿时代距离现在不过400来年,欧几里德和阿基米德却都是公元前古希腊时代的人物。
欧几里德的巨著—《几何原本》【1】(在1607年,有徐光启的中译本【2】),不仅仅被人誉为有史以来最成功的教科书,而且在几何学发展的历史中具有重要意义。其中所阐述的欧式几何是建立在五个公理之上的一套自洽而完整的逻辑理论,简单而容易理解。这点令人惊叹,它标志着在2000多年前,几何学就已经成为了一个有严密理论系统和科学方法的学科!
继欧几里德之后,16世纪法国哲学家、数学家笛卡儿(1596~1650年),将坐标的概念引入几何,建立了解析几何。
就平面几何而言,引入坐标的概念就是使用x、y来表示点、线、园等等图形在平面上的相对位置,因而便可以方便地应用解析的方法来处理几何的问题。如此一来,几何问题便成为代数的问题。这种处理方法使几何问题变得简单容易多了。说起来可笑,这种简单容易的方法反而使原来痴迷于求解平面几何难题的中学生们在刚学了解析几何之后,颇有一种失落感。因为解析几何使几何问题有了规范的解法,好像几何不再具有原来的魅力,原来那样有趣的几何学,被“解析”之后,突然间变得黯然失色、索然无味。
当然,谁也无法否认解析几何的诞生象征着几何发展的一个重要里程碑。解析几何不但能处理欧氏几何中的平面问题,还能解决三维空间的问题,以至于推广到更高维空间的几何问题。比如就说在二维和三维空间中吧,解析几何可研究的图形范围大大扩大。对平面曲线来说,欧氏几何中一般只能处理直线和圆。而现在有了坐标及函数的概念之后,直线可以用一次函数表示;圆可以用二次函数表示,二次函数不仅能够表示圆,还能表示椭圆、抛物线、双曲线等其它情形。除此之外,解析几何中还可以用一个任意的方程式f(x,y)=0,来表示所有的平面曲线,这些都使欧氏几何学望尘莫及。如果论及三维空间的话,在解析化之后,还能用三维坐标(x,y,z)和它们的代数方程式,表示各种各样的空间曲线和奇形怪状曲面。进一步谈到更高维的空间,欧几里德几何就更无用武之地了。
再到后来,数学的各个方面都有了巨大发展,特别是如我们在第一篇中所叙述的,牛顿和莱布尼茨发明了微积分,这是科学上的一件大事,使得那个时代的整个数学和物理都改变了面貌。那么,它对几何学的发展又有何种影响呢?
数学家们自然地将微积分这个强有力的工具用来研究几何学。实际上,微积分和几何的联系还更紧密一些,微积分的诞生也是得益于几何研究的,两者相互影响和发展。因此,微积分诞生之后不久,便有了“微分几何”这门新学科的萌芽。
法国数学家亚历克西斯·克莱洛(Alexis Clairaut ,1713 - 1763))是微分几何的先行者之一【3】。克莱洛是个名副其实的神童,他是母亲生下的20个子女中唯一一个长大成人的。在身为数学教授的父亲的严格管教和高标准要求下,克莱洛9岁开始读《几何原本》,13岁时就在法国科学院宣读他的数学论文。
之后几年,克莱洛迷上了空间曲线,他用曲线在两个垂直平面上的投影来研究空间曲线,第一次研究了空间曲线的曲率和挠率(当时被他称之为:双重曲率)。1729年,16岁的克莱洛将这个结果提交给法国科学院并以此申请法国科学院院士的资格,但当时未得到国王的立即认可。不过,只在两年之后,克莱洛发表了《关于双重曲率曲线的研究》一文,文中他公布了对空间曲线的研究成果,除了提出双重曲率之外,还认识到在一个垂直于曲线的切线的平面上可以有无数多条法线,同时给出了空间曲线的弧长公式,以及曲面的几个基本概念:长度、切线和双重曲率。这一年,18岁的克莱洛成为法国科学院有史以来最年轻的院士。
曲率和挠率是什么?我们先从平面曲线来认识曲率。

图2-1-1:克莱洛及双重曲率
我们首先需要引进曲线的切线,或称之为“切矢量”的概念,切矢量即为当曲线上两点无限接近时它们的连线的极限位置所决定的那个矢量。图2-1-1b中所标示的所有箭头,便是曲线的切矢量在曲线上各个点的直观图像。然后,再从图中切矢量沿着曲线的变化规律,又可以得到曲率的直观概念:曲率表征曲线的弯曲程度。比如说,图2-1-1b中最上面一条是直线,直线不会拐弯,其弯曲程度为0,即曲率等于0。这个0曲率与切矢量的变化是有关系的。看看直线上的箭头就容易明白了:上面所有箭头方向都是同样的。也就是说,曲率就是切矢量方向的变化率,或切矢量的旋转速率。直线上的切矢量方向不变,不旋转,对应于曲率为0。再看看图2-1-1b中下面两条曲线,当弧长增加时,切矢量不断旋转,曲线也随之而弯曲,切矢量旋转得越快,曲线的弯曲程度也越大。所以,曲率的几何意义就是曲线的切矢量对于弧长的旋转速度。
刚才在描述切矢量时,我们说它是“连线的极限位置所决定的那个矢量”,这儿我们很轻松地用上了“极限”的概念,诸位也毫不费力地就理解了它,因为大家学过了微积分。但是,在克莱洛的年代,曲率的计算可不是那么轻松容易的,这个十几岁的神童,天才地把微分的思想用于研究曲线,首次得到了这个结果。不仅如此,刚才我们讨论的只是平面曲线,克莱洛将微积分思想用于空间曲线。对一条平面曲线来说,如果每一点的曲率都确定了,这条曲线的形状便确定了。比如说,很容易直观地看出,一个圆上每个点的曲率都是一样的,等于它的半径的倒数。圆的半径越小,倒数则大,因而曲率便也越大;圆的半径越大,曲率则越小。因此,圆是等曲率的曲线,那么,现在我们考虑图2-1-2a中所示的平面螺旋线。因为平面螺旋线从内看到外,近似于一个一个从小到大的圆,所以,它的曲率是中心大边沿小。
我们可以将这个平面螺旋线想象成一个被压到一个平面上的的锥形弹簧,如果压力撤销之后,锥形弹簧恢复它的三维形状如图2-1-2b所示,这便得到了一条三维曲线。
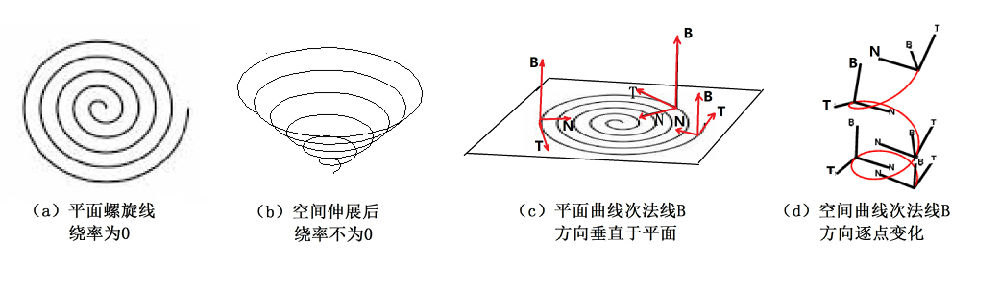
图2-1-2:空间曲线的挠率
首先让我们研究一下将平面螺旋线放在三维空间中的情形。如图2-1-2c所示,这时可以在曲线的每一个点定义一个由3个矢量组成的三维标架。令曲线的切线方向为T,在曲线所在的平面上有一个与T垂直的方向N。如果对于圆周来说,N的方向沿着半径指向圆心。N被称之为曲线在该点的主法线。为什么在法线的前面要加上一个“主”字呢,因为与切线T垂直的矢量不止一个,它们有无穷多个,都可以称为曲线在该点的法线,这些法线构成一个平面,叫做通过该点的法平面。刚才说过,这个事实是首先被小天才克莱洛认识到的。这所有的法线中,有一个是比较特别的,对平面曲线来说就是在此平面上的那一条法线,被称为主法线。有了切线T和主法线N,使用右手定则可以定义出三维空间中的另一个矢量B,B也是法线之一,称之为次法线。从图c很容易看出,螺旋线上每个点的切矢量T和主法线N的方向都逐点变化,唯有次法线B的方向不变。对一般的平面曲线也是如此,次法线的方向永远是垂直于曲线所在平面的,因此,一条平面曲线上每个点的次法线都指向同一个方向,即指向与该平面垂直的方向。
对一般的空间曲线,情况有所不同。想象一下让平面螺旋线中的每一圈逐渐从原来所在的平面慢慢被拉开,这时候,每一点次法线的方向便会从原来的垂直线逐渐发生偏离。也可以说,次法线的方向代表了与曲线“密切相贴”的那个平面,在一般三维曲线的情形下,这个密切相贴的平面逐点不一样,被称为曲线在这个点的“密切平面”。如图2-1-2d所示,对一般的三维曲线而言,在曲线上不同的点,三个标架T、N、B的方向都有所不同了。每一点的次法线B的方向也会变化,不过它仍然与该点的密切平面垂直。
克莱洛注意到空间曲线与平面曲线的不同,认为需要用另外一个曲率,后人称之为“挠率”的几何量来表征这种差别。换言之,挠率可以表示曲线偏离平面曲线的程度,被定义为次法线B随弧长变化的速率。
参考资料:
【1】Heath,Thomas L. (1956). The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile.Original publication: Cambridge University Press, 1925] ed.). New York: DoverPublications.
【2】1607Chinese translations reprinted as part of Siku Quanshu, or "CompleteLibrary of the Four Treasuries."
【3】O'Connorand, J. J.; E. F. Robertson (October 1998). "Alexis Clairaut".MacTutor History of Mathematics Archive. School of Mathematics and Statistics,University of St Andrews, Scotland. Retrieved 2009-03-12.
http://www.zhihu.com/question/27870371
为什么光速不能叠加?
http://www.zhihu.com/question/27870371
为什么光速不能叠加?
如题 就比如那个在光速船上的光速度为什么不是2c而是c
另外我还是不太懂光的传播方式 这和光速不能叠加有关系吗
请各位大神用比较简洁明了的方式解释 物理小白谢谢各位~
另外我还是不太懂光的传播方式 这和光速不能叠加有关系吗
请各位大神用比较简洁明了的方式解释 物理小白谢谢各位~
按投票排序按时间排序
6 个回答
硼铝镓铟铊、F anonymity、杨晓堃 赞同
不是“光速不能叠加”,而是任何一个参照系变换都不能简单地求矢量相加。
只不过在低速状态下,矢量求和的误差很小,所以可以粗略的认为“能”相加,而在速度趋近于光速的时候,直接相加的误差就太大了。
至于“到了光速”,由于物理量不再收敛,光速粒子不能作为参照系,也就没有“叠加”的问题。
只不过在低速状态下,矢量求和的误差很小,所以可以粗略的认为“能”相加,而在速度趋近于光速的时候,直接相加的误差就太大了。
至于“到了光速”,由于物理量不再收敛,光速粒子不能作为参照系,也就没有“叠加”的问题。
杨文豪、知乎用户 赞同
可以这样通俗地理解
快速移动的物体,我们看来时间就会减慢,也就会做“慢动作”
高速运行的飞船本身就在做“慢动作”,它所发出的光也在做“慢动作”,以“比较慢的光速”离开飞船。
而这个“比较慢的光速”叠加上飞船本身的速度,在我们看来正好等于正常的光速
快速移动的物体,我们看来时间就会减慢,也就会做“慢动作”
高速运行的飞船本身就在做“慢动作”,它所发出的光也在做“慢动作”,以“比较慢的光速”离开飞船。
而这个“比较慢的光速”叠加上飞船本身的速度,在我们看来正好等于正常的光速
首先,你應該要清楚自己到底做了什麼假設.相對論的一個結論是"飛船等有質量的物體是不可能達到光速的",而你的前提是"光速飛船",換句話說,你已經預設了"相對論已經被證僞"這樣一個大前提,後面的討論還有什麼意義呢,就算推出和相對論矛盾的結論也很正常嘛.
所以我現在把你的問題第一行改爲:
光速和飛船的速度當然可以疊加.但是,既然你是把這當作一個相對論的(而不是經典力學的)問題來考慮,那就要按相對論的速度疊加方程來算:
 .
.
算出來的結果還是是c.
至於1.9c,那是經典力學的計算結果,但是在高速運動時經典力學是不適用的.
所以我現在把你的問題第一行改爲:
"速度爲的飛船上的光的速度在我們看來爲什麼不是
而是
".
光速和飛船的速度當然可以疊加.但是,既然你是把這當作一個相對論的(而不是經典力學的)問題來考慮,那就要按相對論的速度疊加方程來算:
算出來的結果還是是c.
至於1.9c,那是經典力學的計算結果,但是在高速運動時經典力學是不適用的.
硼铝镓铟铊、F anonymity 赞同
因为你平常熟悉的那套速度相加减法则是Galileo变换下的空间和时间坐标变换,这一变换只是在低速、弱引力下才近似成立(虽然日常中近似的相当好)。经典情况下,在不同惯性参考系中观察(注意,这里的观察和“看”不是一个概念)同一物理现象时所描述的时间和空间坐标服从矢量法则,就像题主简单的理解的速度相加,比如人在车上行走,人相对于大地这个参考系的速度等于人相对于车这个参考系的速度加上车相对于大地的速度(严格来说不是速度相加,应该是位置矢量相加,因为所有参考系有一个相同的“绝对时间”,所以求速度的时候才是相加)。但是这个变换在Maxwell方程出现以后就有问题了。Maxwell方程是描述电磁场性质的方程,从Maxwell方程中求解电磁波传播的波动方程得到的结果是真空中光速是和参考系无关的常数(题主可以简单理解为电磁理论得到真空光速是常数),而且有意思的是Maxwell方程并没有指定适用的参考系。那么这一点就和经典的Galileo变换不符合啊,所以有人就认为Maxwell方程适用于一个绝对参考系(可以理解为宇宙中有一个上帝设置的原点,在那里建立标架),叫做“以太”。不过后来的天文观测(如光行差现象)、光学干涉实验(像Michelson-Morley实验)等等都没有观察到我们大地相对于这个绝对参考系的速度,换句简单的话说就是在各种条件下测到的真空中的光速都是一样的,包括题主说的这种情况(虽然没有在光速的船上测)。然后Einstein就提出来根本不存在这一绝对的参考系,光速在任何参考系中都是不变的(不过话说回来,Lorentz变换是在更早之前就被提出来的诶~)。这是一个假设,但是是一个相当合理自洽并且符合实验结果的假设。所以题主的问题,在一定程度上可以得到回答了。那么这时候,如果真的有一个参考系相对于大地(即另一个参考系)以光速运动,在这两个参考系里面观察同一个物理现象的时候应该怎么变换两个参考系得到的结果呢?应该是按Lorentz变换来进行。而得到Lorentz变换的公式就是严格按照Einstein的两个假设外加时间均匀性(简单理解就是一个参考系里面的时钟走时速度不变),描述光的几种传播方式在不同参考系中观察得到(这里是指同一个现象在不同参考系中观察)一维的Lorentz变换,然后做空间转动变换得到三维的。输公式挺麻烦的,题主如果感兴趣的话可以自己找一下一维Lorentz变换的公式。事情到这里并没有完,Lorentz变换的物理意义还是不够直观、明确,后来有人建立了Minkowski空间(俗称的“四维空间”,不过有的地方时间维度用的是虚数,有的地方引入了协变和逆变所以四个维度都是实数,个人更喜欢后者因为指标升降用起来挺方便的而且度规能够和广相联系),发现Lorentz变换就是Minkowski空间中、保持空间体积元不变的变换(构成了一个Lorentz群),换句话说就是保持“时空间隔”不变的变换,再简单点说就是四维时空中的两个点之间的距离(这里的距离要坐标差乘以度规求和)在Lorentz变换下不变,Lorentz变换就是一个类似三维空间中转动的“转动变换”,试想你把笔转一个角度笔的长度总不会变化吧。从这个角度说,就是你在两个参考系中测量速度时的时间和空间点坐标在四维时空中间隔不变,导致你测到的光速结果不变(话说这么解释好像有点用结论证明前提的感觉。。)。由于同一个物理现象在不同参考系、不同规范中观察和计算应该有同样的结果,所以Lorentz协变性和规范不变性是物理理论应该满足的两个非常重要的性质。所以题主,不是光速不能叠加,而是你要用Lorentz变换做叠加才能得到正确的结论。
至于题主问的光的传播方式,就是电磁波的电场和磁场分量在空间中“振动”着传播啊,传播的时候服从Maxwell方程给出的速度、边界情况(严格来说这是可微或者连续的要求)和衰减情况,然后Maxwell方程给出的传播速度就是一定值,不随着参考系变化。
还有感觉这个答案不够简洁,不知道题主能不能看懂或者符合题主的要求。。。
value proposition tam
Piper Jaffray initiates coverage on CyberArk Software (NASDAQ: CYBR) with a Neutral rating and a price target of $54, which compares to yesterday's close of $62.87.
Analyst Andrew Nowinski commented, "Our thesis is based on four primary factors. First, we believe CyberArk is one of the few vendors that can effectively secure “privileged accounts,” which are essentially “keys to the kingdom.” Second, CyberArk offers one of the most comprehensive platforms in the industry, designed to protect privileged accounts. We also believe the increased adoption of CyberArk’s other products should lead to an acceleration in billings growth. However, our primary concern is that CyberArk’s total addressable market is still small and requires significant education, which could lead to extended sales cycles and lumpy revenue growth."
For an analyst ratings summary and ratings history on CyberArk Software click here. For more ratings news on CyberArk Software click here.
Shares of CyberArk Software closed at $62.87 yesterday.
至于题主问的光的传播方式,就是电磁波的电场和磁场分量在空间中“振动”着传播啊,传播的时候服从Maxwell方程给出的速度、边界情况(严格来说这是可微或者连续的要求)和衰减情况,然后Maxwell方程给出的传播速度就是一定值,不随着参考系变化。
还有感觉这个答案不够简洁,不知道题主能不能看懂或者符合题主的要求。。。
value proposition tam
Piper Jaffray initiates coverage on CyberArk Software (NASDAQ: CYBR) with a Neutral rating and a price target of $54, which compares to yesterday's close of $62.87.
Analyst Andrew Nowinski commented, "Our thesis is based on four primary factors. First, we believe CyberArk is one of the few vendors that can effectively secure “privileged accounts,” which are essentially “keys to the kingdom.” Second, CyberArk offers one of the most comprehensive platforms in the industry, designed to protect privileged accounts. We also believe the increased adoption of CyberArk’s other products should lead to an acceleration in billings growth. However, our primary concern is that CyberArk’s total addressable market is still small and requires significant education, which could lead to extended sales cycles and lumpy revenue growth."
For an analyst ratings summary and ratings history on CyberArk Software click here. For more ratings news on CyberArk Software click here.
Shares of CyberArk Software closed at $62.87 yesterday.


No comments:
Post a Comment