http://www.guokr.com/article/53059/?page=7
喝醉的小鸟

假设有一条水平直线,从某个位置出发,每次有 50% 的概率向左走1米,有50%的概率向右走1米。按照这种方式无限地随机游走下去,最终能回到出发点的概率是多少?答案是100% 。在一维随机游走过程中,只要时间足够长,我们最终总能回到出发点。
现在考虑一个喝醉的酒鬼,他在街道上随机游走。假设整个城市的街道呈网格状分布,酒鬼每走到一个十字路口,都会概率均等地选择一条路(包括自己来时的那条路)继续走下去。那么他最终能够回到出发点的概率是多少呢?答案也还是 100% 。刚开始,这个醉鬼可能会越走越远,但最后他总能找到回家路。
不过,醉酒的小鸟就没有这么幸运了。假如一只小鸟飞行时,每次都从上、下、左、右、前、后中概率均等地选择一个方向,那么它很有可能永远也回不到 出发点了。事实上,在三维网格中随机游走,最终能回到出发点的概率只有大约 34% 。
这个定理是著名数学家波利亚(George Pólya)在 1921 年证明的。随着维度的增加,回到出发点的概率将变得越来越低。在四维网格中随机游走,最终能回到出发点的概率是 19.3% ,而在八维空间中,这个概率只有 7.3%
定理:你永远不能理顺椰子上的毛。
想象一个表面长满毛的球体,你能把所有的毛全部梳平,不留下任何像鸡冠一样的一撮毛或者像头发一样的旋吗?拓扑学告诉你,这是办不到的。这叫做毛球定理(hairy ball theorem),它也是由布劳威尔首先证明的。用数学语言来说就是,在一个球体表面,不可能存在连续的单位向量场。这个定理可以推广到更高维的空间:对于任意一个偶数维的球面,连续的单位向量场都是不存在的。
毛球定理在气象学上有一个有趣的应用:由于地球表面的风速和风向都是连续的,因此由毛球定理,地球上总会有一个风速为 0 的地方,也就是说气旋和风眼是不可避免的
[PDF]一、背景二、Brown 运动三、随机积分四、Black-Scholes 公式
www.math.zju.edu.cn/.../201232675639784.pdf
轉為繁體網頁
轉為繁體網頁
第6章Brown 运动. 一、背景. 1. Robert Brown. Robert Brown (1773-1858) 英国植物学家. 1823年他注意到:. 如果通过显微镜观察悬浮在水中的花粉颗粒,那么会发现.
随机过程 - SSSidea
[DOC]杭州电子科技大学本科毕业论文文献综述 杭州电子科技大学 ...
数学中竟然还有这样的定理! | 科学人| 果壳网科技有意思
www.guokr.com/article/53059/?page=7
轉為繁體網頁
轉為繁體網頁
隨機過程在量子場論計算中的應用
文/林立
所謂隨機過程,是指在一定的條件下,可能發生也可能不發生的過程,具有不確定性,亦即:具有機率性。
最常見的隨機過程之數學模型就是無規行走(random walk)。大家熟知的布朗運動現象即可利用無規行走來解釋。在無規行走中,最重要的一個物理量就是機率分布函數 。它是表示一個在初始時刻位於原點的質點,經過N步無規行走之後,出現在
。它是表示一個在初始時刻位於原點的質點,經過N步無規行走之後,出現在 的機率。
的機率。
由於在無規行走模型中,我們假設質點每一次行走之步伐大小相同,所花的時間也相同,所以在 中的N即相當於是時間變數。經由條件機率的考量及傅立葉變換的技巧,我們可以推導出
中的N即相當於是時間變數。經由條件機率的考量及傅立葉變換的技巧,我們可以推導出 的路徑積分表達式,其形式和量子力學中時間演化算符(又稱為傳播子)之Feynman路徑積分表達式在數學上相同,有一個一對一的對應[註1]。
的路徑積分表達式,其形式和量子力學中時間演化算符(又稱為傳播子)之Feynman路徑積分表達式在數學上相同,有一個一對一的對應[註1]。
有哪些看似荒谬,其实很科学的理论? - 社会- 知乎
www.zhihu.com/question/27282113
轉為繁體網頁
轉為繁體網頁
有哪些美(牛)到不行的理科公式? - 物理学- 知乎
www.zhihu.com/question/26292855
轉為繁體網頁
轉為繁體網頁
蒙特卡罗法对布朗运动的模拟_百度文库
wenku.baidu.com/view/a8772447b307e87101f6965c.html
轉為繁體網頁
轉為繁體網頁
随机游动_CNKI学问
xuewen.cnki.net/R2006072850002538.html
轉為繁體網頁
轉為繁體網頁
随机游动模型_CNKI学问
xuewen.cnki.net/R2008060430001270.html
轉為繁體網頁
轉為繁體網頁
从前有个数- 人人小站
zhan.renren.com/congqianyougeshu?tagId=13389...
轉為繁體網頁
轉為繁體網頁
Uncategorized | 笑对人生,傲立寰宇| 第2 页
https://dahuasky.wordpress.com/category/uncategorized/...
轉為繁體網頁
轉為繁體網頁
数学中竟然还有这样的定理!
好玩的数学定理 数学一点不枯燥 好玩的数学
matrix67 发表于 2011-07-24 15:40
谁说数学是枯燥的?在数学里,有很多欢乐而又深刻的数学定理。这些充满生活气息的数学定理,不但深受数学家们的喜爱,在数学迷的圈子里也广为流传。

定理:喝醉的酒鬼总能找到回家的路,喝醉的小鸟则可能永远也回不了家。
假设有一条水平直线,从某个位置出发,每次有 50% 的概率向左走1米,有50%的概率向右走1米。按照这种方式无限地随机游走下去,最终能回到出发点的概率是多少?答案是100% 。在一维随机游走过程中,只要时间足够长,我们最终总能回到出发点。
现在考虑一个喝醉的酒鬼,他在街道上随机游走。假设整个城市的街道呈网格状分布,酒鬼每走到一个十字路口,都会概率均等地选择一条路(包括自己来时的那条路)继续走下去。那么他最终能够回到出发点的概率是多少呢?答案也还是 100% 。刚开始,这个醉鬼可能会越走越远,但最后他总能找到回家路。
不过,醉酒的小鸟就没有这么幸运了。假如一只小鸟飞行时,每次都从上、下、左、右、前、后中概率均等地选择一个方向,那么它很有可能永远也回不到 出发点了。事实上,在三维网格中随机游走,最终能回到出发点的概率只有大约 34% 。
这个定理是著名数学家波利亚(George Pólya)在 1921 年证明的。随着维度的增加,回到出发点的概率将变得越来越低。在四维网格中随机游走,最终能回到出发点的概率是 19.3% ,而在八维空间中,这个概率只有 7.3% 。

定理:把一张当地的地图平铺在地上,则总能在地图上找到一点,这个点下面的地上的点正好就是它在地图上所表示的位置。
也就是说,如果在商场的地板上画了一张整个商场的地图,那么你总能在地图上精确地作一个“你在这里”的标记。
1912 年,荷兰数学家布劳威尔(Luitzen Brouwer)证明了这么一个定理:假设 D 是某个圆盘中的点集,f 是一个从 D 到它自身的连续函数,则一定有一个点 x ,使得 f(x) = x 。换句话说,让一个圆盘里的所有点做连续的运动,则总有一个点可以正好回到运动之前的位置。这个定理叫做布劳威尔不动点定理(Brouwer fixed point theorem)。
除了上面的“地图定理”,布劳威尔不动点定理还有很多其他奇妙的推论。如果取两张大小相同的纸,把其中一张纸揉成一团之后放在另一张纸上,根据布劳威尔不动点定理,纸团上一定 存在一点,它正好位于下面那张纸的同一个点的正上方。
这个定理也可以扩展到三维空间中去:当你搅拌完咖啡后,一定能在咖啡中找到一个点,它在搅拌前后的位置相同(虽然这个点在搅拌过程中可 能到过别的地方)。

定理:你永远不能理顺椰子上的毛。
想象一个表面长满毛的球体,你能把所有的毛全部梳平,不留下任何像鸡冠一样的一撮毛或者像头发一样的旋吗?拓扑学告诉你,这是办不到的。这叫做毛球定理(hairy ball theorem),它也是由布劳威尔首先证明的。用数学语言来说就是,在一个球体表面,不可能存在连续的单位向量场。这个定理可以推广到更高维的空间:对于任意一个偶数维的球面,连续的单位向量场都是不存在的。
毛球定理在气象学上有一个有趣的应用:由于地球表面的风速和风向都是连续的,因此由毛球定理,地球上总会有一个风速为 0 的地方,也就是说气旋和风眼是不可避免的。

定理:在任意时刻,地球上总存在对称的两点,他们的温度和大气压的值正好都相同。
波兰数学家乌拉姆(Stanisław Marcin Ulam)曾经猜想,任意给定一个从 n 维球面到 n 维空间的连续函数,总能在球面上找到两个与球心相对称的点,他们的函数值是相同的。1933 年,波兰数学家博苏克(Karol Borsuk)证明了这个猜想,这就是拓扑学中的博苏克-乌拉姆定理(Borsuk–Ulam theorem)。
博苏克-乌拉姆定理有很多推论,其中一个推论就是,在地球上总存在对称的两点,他们的温度和大气压的值正好都相同(假设地球表面各地的温度差异和大气压差异是连续变化的)。这是因为,我们可以把温度值和大气压值所有可能的组合看成平面直角坐标系上的点,于是地球表面各点的温度和大气压变化情况就可以看作是二维球面到二维平面的函数,由博苏克-乌拉姆定理便可推出,一定存在两个函数值相等的对称点。
当 n = 1 时,博苏克-乌拉姆定理则可以表述为,在任一时刻,地球的赤道上总存在温度相等的两个点。对于这个弱化版的推论,我们有一个非常直观的证明方法:假设赤道上有 A、B 两个人,他们站在关于球心对称的位置上。如果此时他们所在地方的温度相同,问题就已经解决了。下面我们只需要考虑他们所在地点的温度一高一低的情况。不妨假设,A 所在的地方是 10 度,B 所在的地方是 20 度吧。现在,让两人以相同的速度相同的方向沿着赤道旅行,保持两人始终在对称的位置上。假设在此过程中,各地的温度均不变。旅行过程中,两人不断报出自己 当地的温度。等到两人都环行赤道半周后,A 就到了原来 B 的位置,B 也到了 A 刚开始时的位置。在整个旅行过程中,A 所报的温度从 10 开始连续变化(有可能上下波动甚至超出 10 到 20 的范围),最终变成了 20;而 B 经历的温度则从 20 出发,最终连续变化到了 10。那么,他们所报的温度值在中间一定有“相交”的一刻,这样一来我们也就找到了赤道上两个温度相等的对称点。
定理:任意给定一个火腿三明治,总有一刀能把它切开,使得火腿、奶酪和面包片恰好都被分成两等份。
而且更有趣的是,这个定理的名字真的就叫做“火腿三明治定理”(ham sandwich theorem)。它是由数学家亚瑟•斯通(Arthur Stone)和约翰•图基(John Tukey)在 1942 年证明的,在测度论中有着非常重要的意义。
火腿三明治定理可以扩展到 n 维的情况:如果在 n 维空间中有 n 个物体,那么总存在一个 n - 1 维的超平面,它能把每个物体都分成“体积”相等的两份。这些物体可以是任何形状,还可以是不连通的(比如面包片),甚至可以是一些奇形怪状的点集,只要满足点集可测就行了。
喝醉的小鸟

假设有一条水平直线,从某个位置出发,每次有 50% 的概率向左走1米,有50%的概率向右走1米。按照这种方式无限地随机游走下去,最终能回到出发点的概率是多少?答案是100% 。在一维随机游走过程中,只要时间足够长,我们最终总能回到出发点。
现在考虑一个喝醉的酒鬼,他在街道上随机游走。假设整个城市的街道呈网格状分布,酒鬼每走到一个十字路口,都会概率均等地选择一条路(包括自己来时的那条路)继续走下去。那么他最终能够回到出发点的概率是多少呢?答案也还是 100% 。刚开始,这个醉鬼可能会越走越远,但最后他总能找到回家路。
不过,醉酒的小鸟就没有这么幸运了。假如一只小鸟飞行时,每次都从上、下、左、右、前、后中概率均等地选择一个方向,那么它很有可能永远也回不到 出发点了。事实上,在三维网格中随机游走,最终能回到出发点的概率只有大约 34% 。
这个定理是著名数学家波利亚(George Pólya)在 1921 年证明的。随着维度的增加,回到出发点的概率将变得越来越低。在四维网格中随机游走,最终能回到出发点的概率是 19.3% ,而在八维空间中,这个概率只有 7.3% 。
“你在这里”

也就是说,如果在商场的地板上画了一张整个商场的地图,那么你总能在地图上精确地作一个“你在这里”的标记。
1912 年,荷兰数学家布劳威尔(Luitzen Brouwer)证明了这么一个定理:假设 D 是某个圆盘中的点集,f 是一个从 D 到它自身的连续函数,则一定有一个点 x ,使得 f(x) = x 。换句话说,让一个圆盘里的所有点做连续的运动,则总有一个点可以正好回到运动之前的位置。这个定理叫做布劳威尔不动点定理(Brouwer fixed point theorem)。
除了上面的“地图定理”,布劳威尔不动点定理还有很多其他奇妙的推论。如果取两张大小相同的纸,把其中一张纸揉成一团之后放在另一张纸上,根据布劳威尔不动点定理,纸团上一定 存在一点,它正好位于下面那张纸的同一个点的正上方。
这个定理也可以扩展到三维空间中去:当你搅拌完咖啡后,一定能在咖啡中找到一个点,它在搅拌前后的位置相同(虽然这个点在搅拌过程中可 能到过别的地方)。
不能抚平的毛球

想象一个表面长满毛的球体,你能把所有的毛全部梳平,不留下任何像鸡冠一样的一撮毛或者像头发一样的旋吗?拓扑学告诉你,这是办不到的。这叫做毛球定理(hairy ball theorem),它也是由布劳威尔首先证明的。用数学语言来说就是,在一个球体表面,不可能存在连续的单位向量场。这个定理可以推广到更高维的空间:对于任意一个偶数维的球面,连续的单位向量场都是不存在的。
毛球定理在气象学上有一个有趣的应用:由于地球表面的风速和风向都是连续的,因此由毛球定理,地球上总会有一个风速为 0 的地方,也就是说气旋和风眼是不可避免的。
气候完全相同的另一端

波兰数学家乌拉姆(Stanisław Marcin Ulam)曾经猜想,任意给定一个从 n 维球面到 n 维空间的连续函数,总能在球面上找到两个与球心相对称的点,他们的函数值是相同的。1933 年,波兰数学家博苏克(Karol Borsuk)证明了这个猜想,这就是拓扑学中的博苏克-乌拉姆定理(Borsuk–Ulam theorem)。
博苏克-乌拉姆定理有很多推论,其中一个推论就是,在地球上总存在对称的两点,他们的温度和大气压的值正好都相同(假设地球表面各地的温度差异和大气压差异是连续变化的)。这是因为,我们可以把温度值和大气压值所有可能的组合看成平面直角坐标系上的点,于是地球表面各点的温度和大气压变化情况就可以看作是二维球面到二维平面的函数,由博苏克-乌拉姆定理便可推出,一定存在两个函数值相等的对称点。
当 n = 1 时,博苏克-乌拉姆定理则可以表述为,在任一时刻,地球的赤道上总存在温度相等的两个点。对于这个弱化版的推论,我们有一个非常直观的证明方法:假设赤道上有 A、B 两个人,他们站在关于球心对称的位置上。如果此时他们所在地方的温度相同,问题就已经解决了。下面我们只需要考虑他们所在地点的温度一高一低的情况。不妨假设,A 所在的地方是 10 度,B 所在的地方是 20 度吧。现在,让两人以相同的速度相同的方向沿着赤道旅行,保持两人始终在对称的位置上。假设在此过程中,各地的温度均不变。旅行过程中,两人不断报出自己 当地的温度。等到两人都环行赤道半周后,A 就到了原来 B 的位置,B 也到了 A 刚开始时的位置。在整个旅行过程中,A 所报的温度从 10 开始连续变化(有可能上下波动甚至超出 10 到 20 的范围),最终变成了 20;而 B 经历的温度则从 20 出发,最终连续变化到了 10。那么,他们所报的温度值在中间一定有“相交”的一刻,这样一来我们也就找到了赤道上两个温度相等的对称点。
平分火腿三明治
而且更有趣的是,这个定理的名字真的就叫做“火腿三明治定理”(ham sandwich theorem)。它是由数学家亚瑟•斯通(Arthur Stone)和约翰•图基(John Tukey)在 1942 年证明的,在测度论中有着非常重要的意义。
火腿三明治定理可以扩展到 n 维的情况:如果在 n 维空间中有 n 个物体,那么总存在一个 n - 1 维的超平面,它能把每个物体都分成“体积”相等的两份。这些物体可以是任何形状,还可以是不连通的(比如面包片),甚至可以是一些奇形怪状的点集,只要满足点集可测就行了。
空间点过程与随机测度(二):测度的故事
既然这个Topic的题目是关于随机测度,那么,自然是离不开“测度”(measure)这个概念的。所以在这篇文章里,我们要说一说测度。也许,在很多朋友的眼中,“测度”是一个特别理论的概念——似乎只有研究数学的人才应该关心它。这也许和大学的课程设计有关系,因为这个概念一般是在研究生的数学课程才会开始讲授,比如“实分析”或者“现代概率理论”。而且,在大多数教科书里面,它的第一次出场就已经带着厚厚的面纱——在我看过的大部分教材里面,它总是定义在sigma代数之上,而sigma代数听上去似乎是一个很玄乎的名词。
还是回到我们数星星的例子。

在这个例子里面,我们定义了一“数星星”函数,用符号N表示。这个函数的输入是一个集合(比如A和B),输出是一个数字——该集合中所包含的“星星”的数目。我们看看,这个函数有什么特点。首先,它是非负的,也就是说不可能在一个区域中含有“负数”个星星。其次,它有“可加性”。这是什么意思呢?
比如说,在上面两个不相交的区域A和B里面,各自包含了5个和44个点。那么在A和B的并集总共包含了49个点。换言之,N(A U B) = N(A) + N(B)。
严格一点的说,如果一个“集合函数”,或者说一个从集合到非负实数的映射,如果它在有限个不相交集合的并集上取的值,等于它在这些集合上分别取的值的和,那么我们就认为这个函数具有“可加性”。更进一步的,如果它在可数无限个不相交集合的并集上符合这样的可加性,那么我们就说,它是“可数可加”(Countably additive)。
一个非负“集合函数”,如果对空集取值为0,并且在“一系列集合上”具有可列可加性,那么这个“集合函数”就叫做一个“测度”(Measure)。作为例子,上面的“数星星”函数就是定义在所有二维空间子集上的一个测度。同样的,我们可以举出,很多具体的“测度”的例子,比如:
这里要注意的是,“没法定义面积”和“面积为零”是两回事。比如,在二维集合上的单个离散点或者直线,面积都是零。而那些“没法定义面积”的子集——我们称之为“不可测集”都是一些非常非常奇怪的集合——对于这些集合,我们把它的面积定义为零,或者别的什么非零的数,都会导致自相矛盾。这样的集合是数学家们用特殊的巧妙方法构造出来的——在实际生活中大家是肯定不会碰到的。这样的构造并不困难,但是很巧妙。有兴趣的朋友可以在几乎每本讲测度论的教科书中找到这种构造,这里就不详细说了。

(注:上图不是我制作的,而是出自http://www.daviddarling.info/)
关于不可测 集,有一个很著名的“悖论”,叫做“巴拿赫-塔斯基分球悖论”(Banach-Tarski Paradox)。如果说,某些奇怪的集合不能定义出面积还能让很多人勉强接受的话,那么“塔斯基分球”可能会让很多人“简直无法接受”——包括在上世纪二三十年代的很多著名数学家。这个“怪论”是这么说的:
这个分球术可以通过抽象代数里面对于自由群的分解来实现。对于塔斯基分球有兴趣的朋友,可以参考Leonard M. Wapner的数学读本The Pea and the sun: a mathematical paradox。
细心的朋友可能注意到了,不可测集的构造也好,塔斯基分球也好,都是基于对“选择公理”(Axiom of Choice)的承认。如果我们不承认它,不就没事了么?在我们拒绝承认“选择公理”之前,我们首先要知道“选择公理”究竟是什么东西。通俗一点的说,选择公理可以这么描述:
在历史上,巴拿赫和塔斯基提出分球悖论的年代,正是数学家们对选择公理的存废进行激烈争论的年代。数学家们分成两派,一派支持“选择公理”,另外一派则反对它。而巴拿赫和塔斯基这两位数学天才在当时原是反对接受选择公理,所以它们煞费苦心找到这个分球方法,目的就是以这种令人难以接受的“荒谬现象”来否定选择公理。而在后来的发展中,大部分数学家还是认识到选择公理对于现代数学发展的重要意义(比如,泛函分析中的核心定理——Hahn Banach延拓定理就依赖于对选择公理的承认),而选择接受它,当然塔斯基分球这种“怪现象”也被接受了。现在,“巴拿赫-塔斯基分球悖论”又被称为“巴拿赫-塔斯基分球定理”——从悖论变成定理了。
数学就是这样一个奇妙的世界。它往往基于我们的生活常识建立起来,但是一旦建立起来就要遵循它本身的发展规律,哪怕它有时候违反“常识”——人们能直观认知的常识是有限的,而数学的威力能把我们带到常识所不能触及的地方。
我们说了不相交集合的并集,以及差集,那么对于一般的并集呢?如果A和B是两个可能相交的集合。那么它们的并集A U B可以分成三个不相交的部分:A – C, B – C,以及C三个部分,这里C是A和B的交集。只要知道交集C的测度,根据不相交并集和差集的测度公式,我们就可以知道A – C, B – C,以及A U B的测度。可是仅仅知道 A 和 B的测度,它们的交集的测度是显然不能确定的——两个即使是同样大小的集合,可能相交很多,甚至重合,也可能不相交。
所以,要有效定义一个测度,我们首先需要确定它在一系列集合以及它们的所有交集上的值。这样,这些集合的所有并集和差集的测度也就给定了。数学家把这种观察归纳成一种代数结构——集合上的Semiring——注意这和抽象代数里面的semiring不是一回事。S是一组集合,如果S中任意两个集合的交集仍在S内,S中任何两个集合的差集都可以表示为S中其它有限个不相交集合的并集,那么S就叫一个semiring。那么,只要对S中的集合定义好测度,那么由这些集合的可数次交集并集差集运算产生的那些集合的测度也就确定了。
一组集合,如果包含空集,并且对可数次交集并集补集运算是封闭的,那么这组集合其实就是一个Sigma代数。从某种意义上说,如果我们确定了一个覆盖全集的semiring上的测度,那么整个sigma代数中所有集合的测度都确定了。这可以和线性空间做一个不太严格的类比。在线性代数里面,对于一个线性函数,如果它在基上的函数值确定了,那么它在整个线性空间的函数值也就确定了。对于测度,semiring好比是“基”,而sigma代数则好比是整个空间。
测度,其实很简单
在这里,我只是想拨开测度的神秘面纱——其实,测度是一个非常简单的事情:理解它,只需要小学生的知识,而不是研究生。还是回到我们数星星的例子。

在这个例子里面,我们定义了一“数星星”函数,用符号N表示。这个函数的输入是一个集合(比如A和B),输出是一个数字——该集合中所包含的“星星”的数目。我们看看,这个函数有什么特点。首先,它是非负的,也就是说不可能在一个区域中含有“负数”个星星。其次,它有“可加性”。这是什么意思呢?
比如说,在上面两个不相交的区域A和B里面,各自包含了5个和44个点。那么在A和B的并集总共包含了49个点。换言之,N(A U B) = N(A) + N(B)。
严格一点的说,如果一个“集合函数”,或者说一个从集合到非负实数的映射,如果它在有限个不相交集合的并集上取的值,等于它在这些集合上分别取的值的和,那么我们就认为这个函数具有“可加性”。更进一步的,如果它在可数无限个不相交集合的并集上符合这样的可加性,那么我们就说,它是“可数可加”(Countably additive)。
一个非负“集合函数”,如果对空集取值为0,并且在“一系列集合上”具有可列可加性,那么这个“集合函数”就叫做一个“测度”(Measure)。作为例子,上面的“数星星”函数就是定义在所有二维空间子集上的一个测度。同样的,我们可以举出,很多具体的“测度”的例子,比如:
- 各个区域内的所有星星的总质量
- 各个区域的面积大小
不可测集和分球悖论
不过,在某些条件下,测度并不能定义在全部子集上。说通俗点,就是对其中一些集合,我们不可能定义出它的测度。比如说,在二维平面,我们可以按照一般的理解定义面积函数,比如长和宽分别为a和b的长方形面积为ab。对于复杂一点的形状,我们可以通过积分来计算面积。但是,是不是所有的二维平面的子集都存在一个“面积”呢?正确的答案显得有点“违背常识”:在承认选择公理(Axiom of Choice)正确的情况下,确实有一些集合没法定义出面积。或者说,无论我们在这些集合上定义面积为多少,都会导致自相矛盾的结果。这里要注意的是,“没法定义面积”和“面积为零”是两回事。比如,在二维集合上的单个离散点或者直线,面积都是零。而那些“没法定义面积”的子集——我们称之为“不可测集”都是一些非常非常奇怪的集合——对于这些集合,我们把它的面积定义为零,或者别的什么非零的数,都会导致自相矛盾。这样的集合是数学家们用特殊的巧妙方法构造出来的——在实际生活中大家是肯定不会碰到的。这样的构造并不困难,但是很巧妙。有兴趣的朋友可以在几乎每本讲测度论的教科书中找到这种构造,这里就不详细说了。

(注:上图不是我制作的,而是出自http://www.daviddarling.info/)
关于不可测 集,有一个很著名的“悖论”,叫做“巴拿赫-塔斯基分球悖论”(Banach-Tarski Paradox)。如果说,某些奇怪的集合不能定义出面积还能让很多人勉强接受的话,那么“塔斯基分球”可能会让很多人“简直无法接受”——包括在上世纪二三十年代的很多著名数学家。这个“怪论”是这么说的:
我们可以把一个三维的半径为1的实心球用某种巧妙方法分成五等分——五等分的意思是,把其中一份旋转平移后可以和另外一份重合——然后把这五个分块旋转平移后,可以组合成两个半径为1的实心球。简单的说,一个球分割重组后变成了两个同样大小的球!当然了,这样的过程还可以继续下去,两个变四个,四个变八个。。。。。。有人说,这显然不正确吧,然后他这么Argue:
如果一个实心球体积为V(因为球的半径是1,所以V > 0),那么五个等分块,每块体积为V/5,平移旋转不改变体积,所以,无论它们如何组合,最后得到的东西总体积是V,而不可能是2V。但是,这样的说法在传统意义下确实没错——你拿去中学老师那里,肯定会被称赞是一个善于思考的好孩子。但是,我在更广义的条件下考察,就有问题了。因为,这个论述是基于这么一个假设:每一个分块都是有“体积”的。而塔斯基分球的精妙之处就在于它把球分成了五个“不可测集”——也就是五个“无法定义体积”的奇怪分块。所以,这里我们说“五等分”只是说它们其中一块平移旋转后能重合到另一块上,并不是说它们“体积相等”——因为根本就没有体积,也就没有相等之说。
这个分球术可以通过抽象代数里面对于自由群的分解来实现。对于塔斯基分球有兴趣的朋友,可以参考Leonard M. Wapner的数学读本The Pea and the sun: a mathematical paradox。
细心的朋友可能注意到了,不可测集的构造也好,塔斯基分球也好,都是基于对“选择公理”(Axiom of Choice)的承认。如果我们不承认它,不就没事了么?在我们拒绝承认“选择公理”之前,我们首先要知道“选择公理”究竟是什么东西。通俗一点的说,选择公理可以这么描述:
任意一组(可能有不可数无限个)非空集合,我们都可以从每个集合挑出一个元素。看上去非常“无辜”啊——这不就是典型的“正确的废话”么——所以它被叫做“公理”。可是就是这么一个公理,却是魔力惊人,能让我们把实心球一个变俩。这就是数学的魅力!
在历史上,巴拿赫和塔斯基提出分球悖论的年代,正是数学家们对选择公理的存废进行激烈争论的年代。数学家们分成两派,一派支持“选择公理”,另外一派则反对它。而巴拿赫和塔斯基这两位数学天才在当时原是反对接受选择公理,所以它们煞费苦心找到这个分球方法,目的就是以这种令人难以接受的“荒谬现象”来否定选择公理。而在后来的发展中,大部分数学家还是认识到选择公理对于现代数学发展的重要意义(比如,泛函分析中的核心定理——Hahn Banach延拓定理就依赖于对选择公理的承认),而选择接受它,当然塔斯基分球这种“怪现象”也被接受了。现在,“巴拿赫-塔斯基分球悖论”又被称为“巴拿赫-塔斯基分球定理”——从悖论变成定理了。
数学就是这样一个奇妙的世界。它往往基于我们的生活常识建立起来,但是一旦建立起来就要遵循它本身的发展规律,哪怕它有时候违反“常识”——人们能直观认知的常识是有限的,而数学的威力能把我们带到常识所不能触及的地方。
测度与集合的代数结构
测度和集合的运算是密切相关的。根据测度的定义,如果A和B是两个不相交的集合,如果A和B的测度被确定之后,它们的并集的测度也就确定了,就等于它们各自测度的和。如果B是A的子集,那么如果它们的测度测定,那么它们的差集A – B的测度也就确定了,等于A和B的测度的差。所以,当我们要定义一个测度的时候,其实往往不需要对所有的集合都作出定义,只要对一部分集合定义好了,其它集合的测度也就确定了。我们说了不相交集合的并集,以及差集,那么对于一般的并集呢?如果A和B是两个可能相交的集合。那么它们的并集A U B可以分成三个不相交的部分:A – C, B – C,以及C三个部分,这里C是A和B的交集。只要知道交集C的测度,根据不相交并集和差集的测度公式,我们就可以知道A – C, B – C,以及A U B的测度。可是仅仅知道 A 和 B的测度,它们的交集的测度是显然不能确定的——两个即使是同样大小的集合,可能相交很多,甚至重合,也可能不相交。
所以,要有效定义一个测度,我们首先需要确定它在一系列集合以及它们的所有交集上的值。这样,这些集合的所有并集和差集的测度也就给定了。数学家把这种观察归纳成一种代数结构——集合上的Semiring——注意这和抽象代数里面的semiring不是一回事。S是一组集合,如果S中任意两个集合的交集仍在S内,S中任何两个集合的差集都可以表示为S中其它有限个不相交集合的并集,那么S就叫一个semiring。那么,只要对S中的集合定义好测度,那么由这些集合的可数次交集并集差集运算产生的那些集合的测度也就确定了。
一组集合,如果包含空集,并且对可数次交集并集补集运算是封闭的,那么这组集合其实就是一个Sigma代数。从某种意义上说,如果我们确定了一个覆盖全集的semiring上的测度,那么整个sigma代数中所有集合的测度都确定了。这可以和线性空间做一个不太严格的类比。在线性代数里面,对于一个线性函数,如果它在基上的函数值确定了,那么它在整个线性空间的函数值也就确定了。对于测度,semiring好比是“基”,而sigma代数则好比是整个空间。
数星星的数学还在继续:随机测度
回到数星星的过程。上面我们讨论过了,数星星其实就是一个测度。可是,每天晚上我们看到的星星分布都在变化的。也就是说,每数一次星星,就会得到一个不同的测度。这和掷骰子有点像。每掷一次骰子,我们的得到一个不同的点数——这个点数可以被看成是一个随机变量,变量的值是1到6的整数。同样的道理,星星的分布不确定,每数一次得到一个不同的测度——这也可以看成是一个“随机变量”,只是这里变量的值是一个测度,而不是一个数字。这样的一种以测度为值的“随机变量”,叫做“随机测度”(Random Measure)。这是在接下来的文章中要继续讲述的故事。空间点过程与随机测度(一):从数星星说起
Blog的更新刚刚恢复,就得到大家的鼓励,真是让我感动,谢谢大家了。

小时候,在晴朗的夜里,我喜欢仰望星空,去数天上的星星——那是无忧无虑的快乐童年。长大后,当我们再度仰望苍穹,也许会思考一个不一样的问题:这点点繁星的分布是不是遵循什么数学规律呢?这个问题也许问得太不解风情了。但是,在这篇文章里,我希望向大家表达的是,这个问题会把我们带入一个比星空更为美丽的数学的世界。
探讨这个问题,不需要什么高深的方法。还是和我们小时候一样,我们从“数星星”做起。相比于整个夜空,每个星星是在太小太小了,所以,我们可以做一个简化的设定:把每颗星星看成是一个点——一个没有大小的点——在我们的讨论中,我们只关心星星的位置和数目,不关心它的大小和形状,更不会关心那上面也许存在的外星人。(在之后的连载中,还会讨论这些星星的重量,以及它们在历史长河中的产生,运动,和消亡。)
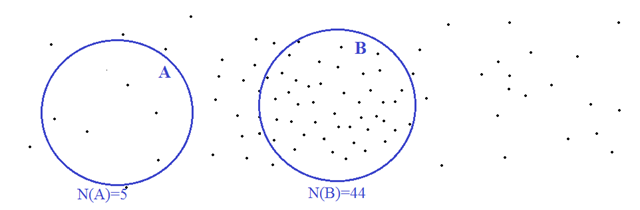
我们开始数星星。为了方便,我们把整个星空分成不相交的区域,然后分区数数。在上面这个图里面,我画出了两个区域:A 和 B。N(A)和N(B)分别表示,这两个区域里面的星星的个数。我们可以看到,星星的分布可能是不均匀的,有些地方稀疏一些,另外一些地方稠密一些。所以,虽然A和B的面积差不多,但是,里面包含的星星数目却相差好多倍。
由于各种各样的原因,我们每天看到的星空中星星的分布可能都在变化。即使同一个区域,里面包含的星星数目也可能是不确定的——这就是概率理论能发挥作用的时候了。对于每个给定的区域,我们认为里面的星星数目是个随机变量,比如上面所说的N(A)和N(B)。为了我们的讨论能够继续进行,需要做出一些简化假设。在这里,我们的假设很简单:
了解现代概率理论的朋友对于almost surely想必是司空见惯了。为了让对这个术语不太熟悉的朋友不产生误解,我还是在这里澄清一下。“几乎肯定发生”和“必然发生”在数学上是有所区别的。举个例子,我们在从 [0, 2] 这个区间的均匀分布中随便抽一个数 a,那么 a 刚刚好等于 1 的概率是多少呢?——是 0。所以,我们可以说,a “几乎肯定”不刚好等于 1。但是,我们不能说 a 必然不等于 1。
这个数星星的例子代表了一类非常广泛的随机过程——空间点过程(Point Processes)。具体来说,什么叫做一个空间点过程呢?我们知道,对于一个(实数值)随机变量,每次抽样(或者试验),得到的是一个实数;对于一个随机向量,每次从分布里面抽取的是一个向量。那么,一个空间点过程,每次抽样得到是在某个空间中的一个离散点集(里面有有限个或者可数无限个点)。在数星星的例子里面,这个空间就是“星空”了。一般来说,这个空间可以是任意的,比如实数集,二维空间,三维空间,曲面,甚至是无限维的函数空间。
最基本的空间点过程,叫做空间泊松过程(Spatial Poisson Process)——一个空间点过程,如果在不相交的区域中的计数是相互独立的,那么这个空间点过程就叫空间泊松过程。虽然,我们没有对N(A)的分布形式作出具体的设定。但是,仅仅凭着不相交区域内计数的独立性,我们就可以得到一个重要的结论:
为什么我们要讨论空间泊松过程呢?它究竟有什么用呢?在我非常有限的知识范围里,我觉得它起码有两个非常重要的意义:
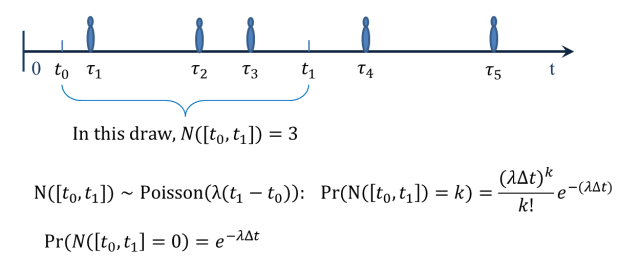
时间上的泊松过程用于描述随机到达,比如来排队的人,或者路过的车子。上面这个图回顾了时间上的泊松过程的一些基本的性质:
上面关于时间点过程的回顾,仅仅是为了说明这篇文章所讲述的内容其实是大家在随机过程课中所学的泊松过程的推广。在下面的讨论中,我们还是回到一般的空间泊松过程。
为了考察这个问题,我们首先对整个空间进行细分,把它分成很多很小的不相交的小格子。

因为每个格子很小,因此对于每个具体的格子,它里面包含点的概率是很低的,而包含不止一个点的概率就更是低到几乎可以忽略了。因此,每个区域中点的数量,大概等于包含点的格子的数量——这样,我们把数点变成了数格子。
假设区域A包含M个格子,它们包含点的概率分别是p_1, p_2, …, p_M。如果我们用X_i表示在第 i 个格子是否存在点,那么 X_i 是一个成功概率为 p_i 的伯努利试验。因而,包含点的格子的总数可以表示为 X_1 + X_2 + … + X_M。因为这些格子不相交,根据不相交区域的独立性假设,X_1, X_2, …, X_M 是相互独立的。在这种条件下,它们的和有一个重要的结论:
在上面,我们通过独立性假设,建立的泊松过程。其实,泊松过程还可以从另外一个方面去刻画。我们知道,对于某个具体的区域,它里面的点数服从泊松分布(假设均值为C)。根据泊松分布的公式,在这个区域为空的概率(点数为零)是 exp(- C) 。这似乎只是一个简单的性质,但是请不要小看它——就这个小小的性质本身(不需要附加独立性假定),就足以定义泊松过程:
所以,一方面,计数的独立性必然导出泊松分布;反过来,泊松分布其也蕴含了独立计数的内在性质。它们是一对孪生兄弟,谁也离不开谁。
这让我们回忆起概率论中非常著名的“中央极限定理”:大量的独立随机变量的和依分布收敛于高斯分布。(我们上面说的是:大量的独立伯努利试验的和依分布收敛于泊松分布)。如果说,中央极限定理奠定了高斯分布(正态分布)在概率论中的核心地位;那么在空间点过程这个领域,上述的关于独立计数和泊松分布的关系,则奠定了泊松分布在空间点过程理论中的核心地位。
很多的其它重要的随机过程,包括Cox过程,Gamma过程,以及Dirichlet过程,都是以泊松过程为基础的。在后面的文章中,还会进一步讨论我们如何从泊松过程出发构造其它过程,特别是“完全随机测度”(Completely Random Measure),而统计建模中被广泛采用的Gamma过程和Dirichlet过程,则是这种构造的一个重要的例子。
数星星的数学
从今天开始,我打算分几篇来分享一个我认为是概率理论中一个非常漂亮的Topic:空间点过程(Point Processes)和随机测度(Random Measure)。
小时候,在晴朗的夜里,我喜欢仰望星空,去数天上的星星——那是无忧无虑的快乐童年。长大后,当我们再度仰望苍穹,也许会思考一个不一样的问题:这点点繁星的分布是不是遵循什么数学规律呢?这个问题也许问得太不解风情了。但是,在这篇文章里,我希望向大家表达的是,这个问题会把我们带入一个比星空更为美丽的数学的世界。
探讨这个问题,不需要什么高深的方法。还是和我们小时候一样,我们从“数星星”做起。相比于整个夜空,每个星星是在太小太小了,所以,我们可以做一个简化的设定:把每颗星星看成是一个点——一个没有大小的点——在我们的讨论中,我们只关心星星的位置和数目,不关心它的大小和形状,更不会关心那上面也许存在的外星人。(在之后的连载中,还会讨论这些星星的重量,以及它们在历史长河中的产生,运动,和消亡。)

我们开始数星星。为了方便,我们把整个星空分成不相交的区域,然后分区数数。在上面这个图里面,我画出了两个区域:A 和 B。N(A)和N(B)分别表示,这两个区域里面的星星的个数。我们可以看到,星星的分布可能是不均匀的,有些地方稀疏一些,另外一些地方稠密一些。所以,虽然A和B的面积差不多,但是,里面包含的星星数目却相差好多倍。
由于各种各样的原因,我们每天看到的星空中星星的分布可能都在变化。即使同一个区域,里面包含的星星数目也可能是不确定的——这就是概率理论能发挥作用的时候了。对于每个给定的区域,我们认为里面的星星数目是个随机变量,比如上面所说的N(A)和N(B)。为了我们的讨论能够继续进行,需要做出一些简化假设。在这里,我们的假设很简单:
1. 对于任意两个不相交的区域A和B,N(A)和N(B)是独立的。对于这两个假设,我需要做些说明。首先,请大家注意,除了说他们独立之外,我没有对N(A)和N(B)的分布形式作出任何假设——后面,我们会看到,为什么不需要假定它们是什么分布。另外,在第二个假设中“几乎肯定”(almost surely)这个术语在数学上是有严格定义的,某个事情“几乎肯定”会发生,表示,它们发生的概率是 1。
2. 两颗星星几乎肯定不会出现在同一个点上。
了解现代概率理论的朋友对于almost surely想必是司空见惯了。为了让对这个术语不太熟悉的朋友不产生误解,我还是在这里澄清一下。“几乎肯定发生”和“必然发生”在数学上是有所区别的。举个例子,我们在从 [0, 2] 这个区间的均匀分布中随便抽一个数 a,那么 a 刚刚好等于 1 的概率是多少呢?——是 0。所以,我们可以说,a “几乎肯定”不刚好等于 1。但是,我们不能说 a 必然不等于 1。
空间点过程
好了,继续回到我们的主题。这个数星星的例子代表了一类非常广泛的随机过程——空间点过程(Point Processes)。具体来说,什么叫做一个空间点过程呢?我们知道,对于一个(实数值)随机变量,每次抽样(或者试验),得到的是一个实数;对于一个随机向量,每次从分布里面抽取的是一个向量。那么,一个空间点过程,每次抽样得到是在某个空间中的一个离散点集(里面有有限个或者可数无限个点)。在数星星的例子里面,这个空间就是“星空”了。一般来说,这个空间可以是任意的,比如实数集,二维空间,三维空间,曲面,甚至是无限维的函数空间。
最基本的空间点过程,叫做空间泊松过程(Spatial Poisson Process)——一个空间点过程,如果在不相交的区域中的计数是相互独立的,那么这个空间点过程就叫空间泊松过程。虽然,我们没有对N(A)的分布形式作出具体的设定。但是,仅仅凭着不相交区域内计数的独立性,我们就可以得到一个重要的结论:
对于任意的区域 A,在A里面的点的数目 N(A) 服从泊松分布(Poisson Distribution)。这里说“任意区域”其实是不太严格的——在正式的数学定理中,泊松过程所基于的空间必须是一个测度空间(measure space),这里的区域A,必须是一个可测集(measurable set)。不熟悉测度理论的朋友可以不妨暂且认为这个区域是任意的吧——因为,在实际常见的几乎所有几何空间里,你能想象出来的集合都是可测集,而不可测的集合只存在于数学家的奇怪构造中。
为什么我们要讨论空间泊松过程呢?它究竟有什么用呢?在我非常有限的知识范围里,我觉得它起码有两个非常重要的意义:
- 在我们所生活的大千世界里,无数的自然现象和科学观测都可以很好地用空间泊松过程来建模和分析。除了天上的星星之外,还有很多很多:天上飞的鸟,水里游的鱼,街上走的人,空气中的分子,放射过程产生的粒子,桌上的灰尘,很多仪器产生的图像中的黑白噪点。。。。。。
- 泊松过程是构造很多别的过程的理论根基所在。了解Machine Learning的朋友应该知道近几年,对非参数化贝叶斯(Non-parametric Bayesian)的研究热火朝天——其中很重要的一种过程叫做狄里克莱过程(Dirichlet Processes)。对于狄里克莱过程,大家耳熟能详的也许是Chinese Restaurant Process,又或者是Stick Breaking。可是,您是否知道,狄里克莱过程的理论根源却是源于空间泊松过程?关于这两种过程的联系,是随机测度理论的一个非常美妙的结果。这我们会留在以后的连载中继续探讨。

时间上的泊松过程用于描述随机到达,比如来排队的人,或者路过的车子。上面这个图回顾了时间上的泊松过程的一些基本的性质:
- 不相交的时间段上到来的数量是相互独立的;
- 两个点几乎肯定不会同时到达;
- 在某个给定的时间段到达的数量服从泊松分布,分布均值正比于时间段的长度。
上面关于时间点过程的回顾,仅仅是为了说明这篇文章所讲述的内容其实是大家在随机过程课中所学的泊松过程的推广。在下面的讨论中,我们还是回到一般的空间泊松过程。
计数独立和泊松分布
看到这里,我想大家也许会有疑问?为什么不相交区域的计数独立,就必然会导致任意给定区域内的计数服从泊松分布呢?作为一篇博客文章,我不可能在这里进行一个严格的证明。但是,我会尝试从更直观的角度来解释这个结论是怎么来的。这里的背后正隐含了独立计数和泊松分布之间的深刻联系。为了考察这个问题,我们首先对整个空间进行细分,把它分成很多很小的不相交的小格子。

因为每个格子很小,因此对于每个具体的格子,它里面包含点的概率是很低的,而包含不止一个点的概率就更是低到几乎可以忽略了。因此,每个区域中点的数量,大概等于包含点的格子的数量——这样,我们把数点变成了数格子。
假设区域A包含M个格子,它们包含点的概率分别是p_1, p_2, …, p_M。如果我们用X_i表示在第 i 个格子是否存在点,那么 X_i 是一个成功概率为 p_i 的伯努利试验。因而,包含点的格子的总数可以表示为 X_1 + X_2 + … + X_M。因为这些格子不相交,根据不相交区域的独立性假设,X_1, X_2, …, X_M 是相互独立的。在这种条件下,它们的和有一个重要的结论:
对于M个独立伯努利试验X_1, X_2, …, X_M,成功概率分别为p_1, p_2, …, p_M,当每个p_i都很小,它们的总和是个常数C,那么 X_1 + X_2 + … + X_M 近似服从以C为均值的泊松分布。当M趋近于无穷大,每个p_i分别趋近于0,并且总和保持为C,那么在极限条件下,X_1 + X_2 + …,严格服从以C为均值的泊松分布。(熟悉概率理论的朋友应该知道,这样的描述其实是指“按分布收敛”。)所以,当我们对空间进行无限细分,在极限条件下,会发生下面的事情:
- 每个格子的大小趋近于零,因而里面包含点的概率趋近于零;
- 同时,某个固定区域内的格子数目趋近于无穷大;
- 一个格子内几乎肯定不会出现两个点,因此某个区域内的点数几乎相等于区域内的包含点的格子数;
- 在这个过程中,某个区域内,所有格子的含点概率的总和维持为一个常数,我们称之为C。
在上面,我们通过独立性假设,建立的泊松过程。其实,泊松过程还可以从另外一个方面去刻画。我们知道,对于某个具体的区域,它里面的点数服从泊松分布(假设均值为C)。根据泊松分布的公式,在这个区域为空的概率(点数为零)是 exp(- C) 。这似乎只是一个简单的性质,但是请不要小看它——就这个小小的性质本身(不需要附加独立性假定),就足以定义泊松过程:
一个空间点过程,如果区域为空的概率随区域的大小(测度)以指数衰减,那么这个过程是一个空间泊松过程。对于这个事情,它的严格证明需要使用Characteristic function的有关理论。但是,尽管不太严格,我们还是可以通过直观的观察对这个结论的原理有所感觉。假定,一个区域的大小(测度)为C,那么如果把它分成很多小格子,每个格子大小(测度)是C_1, …, C_M。那么,显然C = C_1 + … + C_M。因此,这个区域为空的概率有
exp(- C ) = exp(- (C_1 + … + C_M)) = exp(- C_1) exp(- C_2) … exp (- C_M)注意,exp(- C_i) 正是第 i 个细分的小格为空的概率。如果一个概率能够按照乘积分解,其实已经在某种意义上预示了,每个格子是否为空其实是各自独立的,也就是说每个格子是否包含点也是各自独立的——这正好吻合了前面我们对泊松过程的构造。
所以,一方面,计数的独立性必然导出泊松分布;反过来,泊松分布其也蕴含了独立计数的内在性质。它们是一对孪生兄弟,谁也离不开谁。
这让我们回忆起概率论中非常著名的“中央极限定理”:大量的独立随机变量的和依分布收敛于高斯分布。(我们上面说的是:大量的独立伯努利试验的和依分布收敛于泊松分布)。如果说,中央极限定理奠定了高斯分布(正态分布)在概率论中的核心地位;那么在空间点过程这个领域,上述的关于独立计数和泊松分布的关系,则奠定了泊松分布在空间点过程理论中的核心地位。
很多的其它重要的随机过程,包括Cox过程,Gamma过程,以及Dirichlet过程,都是以泊松过程为基础的。在后面的文章中,还会进一步讨论我们如何从泊松过程出发构造其它过程,特别是“完全随机测度”(Completely Random Measure),而统计建模中被广泛采用的Gamma过程和Dirichlet过程,则是这种构造的一个重要的例子。
No comments:
Post a Comment