http://blog.sciencenet.cn/blog-677221-838130.html
反对,不会显示你的姓名
如何理解闵可夫斯基四维时空距离公式中的虚数与负号?
来自: Neo 2013-12-18 15:08:15
长期以来,我们一直在学校与书本中所接受到的关于两点之间距离的公式都是诸如 D^2=A^2+B^2+C^2 这样的,但是在阐述闵可夫斯基四维时空的距离公式中却出现了虚数与负号,为什么会是虚数与负号?
Jim Lee 赞同
大家不要瞎扯了,光速不变只是麦克斯韦方程组的必然推论,根本不是什么第一性原理。
误解来源于语言的不当性。物理学中的很多理解障碍,源于人类提出的问题不恰当、不合理。比如,光的速度是多少?这个问题是不恰当的,因为速度不是一个好的物理量。我们要学会区分物理量的好坏,从而问出有意义的问题。
速度为什么不是好的物理量呢?这跟速度的定义有关。速度是定义为空间对时间的导数。这就隐含了一层意思,就是认为时间是标记物体运动的一个参数,空间坐标是时间的函数,所以我们要了解空间关于时间的变化率,也就是速度。
这种定义明显地把空间和时间放在了不对等的位置上。一个粒子在时空中运动,划过一条世界线。按照狭义相对论的时空观,时空是等价的。粒子不仅在空间方向上运动,也在时间方向上运动。你凭什么要求空间对时间求变化率呢?这就好像你看到一个抛物运动的轨迹以后,问出一个问题:水平位移对垂直位移的变化率是多少?这有意义吗?有意义的问题应该是水平速度和垂直速度分别是多少。水平运动和垂直运动是两个平等的自由度,我们应该分别询问它们关于一个共同参数(比如时间)的变化率,才有意义。
作为类比,在相对论中,时间和空间都变成了平等的自由度,因此我们不能要求一个自由度对另一个自由度求变化率,而是要分别询问,时间和空间关于某个共同参数(比如世界线轨迹)的变化率,这才有意义。所以我们要定义一个有4个分量的速度:它的三个空间分量分别是三个空间坐标对proper time (固有时)的变化率,反映了物体在空间中的运动;还有一个时间分量是时间对 proper time 的变化率,反映了物体在时间方向上的运动。这种速度被称为恰当速度(proper velocity),又称为 velocity 4-vector,它是Lorentz 协变的。我们容易感受到,这样的速度才是好的速度。
这样,我们会发现,即使是一个静止的物体,它其实也在运动。静止的物体沿着时间的方向运动,从过去走向将来,其恰当速度的“大小”(scalar product of velocity 4-vector)正好就是光速。所以从这个意义上说,每一个物体都在时空中以光速运动!光速不是光所特有的,而是一切物体都共有的恰当速度。静止的物体和光的唯一区别就在于,静止的物体把所有的恰当速度都用到了在时间方向上的运动上去了,而光则把恰当速度“平均分配”到时间和空间两个方向上的运动上去。
那么这下好了,所有的物体在时空中的恰当速度都是一样大的,那么我们怎么比较物体运动的快慢呢?由于恰当速度不能够再用于衡量物体的快慢,我们需要专门针对物体的快慢定义一个新的物理量,叫做快度。
快度定义为:arccosh( v0 / c ), 其中v0 是恰当速度的第四分量,c 是真空光速。也许,我们会觉得很奇怪,为什么快度这么复杂的概念反而是一个好的物理量呢?这与我们看问题的角度有关,在狭义相对论的时空观看来,快度是衡量物体运动快慢最自然的物理量。因为它就是时空转动的转角(如果我们把 Lorentz boost 想象成一种旋转的话),从某种意义上,我们可以认为快度衡量了世界线和时间轴的“夹角”。对于静止的物体,世界线沿时间轴方向,夹角为0,所以快度也为0,故称之为静止。对于光来说,比较奇特一些,因为时空是 Minkowski 空间,所以夹角这件事情不是我们直接用量角器可以量出来的。实际上,按照定义式计算,光的快度是无穷大。
光的快度是无穷大,这说明了两个问题:第一,没有任何物体的快度可以比光更大,所以光是最快的;第二,无穷大加减任何有限的快度,仍然是无穷大,所以光在任何有限快度的参考系中,都是无穷快的,也就是说,光速不变。
复制的豆瓣的Everett的回答
srtwin 双胞胎 固有时t类似于普通空间中弧长s的概念。在普通空间中,弧长s表示一条曲线的长度,或者说是一个人走过的路径的长度
速度为什么不是好的物理量呢?这跟速度的定义有关。速度是定义为空间对时间的导数。这就隐含了一层意思,就是认为时间是标记物体运动的一个参数,空间坐标是时间的函数,所以我们要了解空间关于时间的变化率,也就是速度。
这种定义明显地把空间和时间放在了不对等的位置上。一个粒子在时空中运动,划过一条世界线。按照狭义相对论的时空观,时空是等价的。粒子不仅在空间方向上运动,也在时间方向上运动。你凭什么要求空间对时间求变化率呢?这就好像你看到一个抛物运动的轨迹以后,问出一个问题:水平位移对垂直位移的变化率是多少?这有意义吗?有意义的问题应该是水平速度和垂直速度分别是多少。水平运动和垂直运动是两个平等的自由度,我们应该分别询问它们关于一个共同参数(比如时间)的变化率,才有意义。
作为类比,在相对论中,时间和空间都变成了平等的自由度,因此我们不能要求一个自由度对另一个自由度求变化率,而是要分别询问,时间和空间关于某个共同参数(比如世界线轨迹)的变化率,这才有意义。所以我们要定义一个有4个分量的速度:它的三个空间分量分别是三个空间坐标对proper time (固有时)的变化率,反映了物体在空间中的运动;还有一个时间分量是时间对 proper time 的变化率,反映了物体在时间方向上的运动。这种速度被称为恰当速度(proper velocity),又称为 velocity 4-vector,它是Lorentz 协变的。我们容易感受到,这样的速度才是好的速度。
这样,我们会发现,即使是一个静止的物体,它其实也在运动。静止的物体沿着时间的方向运动,从过去走向将来,其恰当速度的“大小”(scalar product of velocity 4-vector)正好就是光速。所以从这个意义上说,每一个物体都在时空中以光速运动!光速不是光所特有的,而是一切物体都共有的恰当速度。静止的物体和光的唯一区别就在于,静止的物体把所有的恰当速度都用到了在时间方向上的运动上去了,而光则把恰当速度“平均分配”到时间和空间两个方向上的运动上去。
那么这下好了,所有的物体在时空中的恰当速度都是一样大的,那么我们怎么比较物体运动的快慢呢?由于恰当速度不能够再用于衡量物体的快慢,我们需要专门针对物体的快慢定义一个新的物理量,叫做快度。
快度定义为:arccosh( v0 / c ), 其中v0 是恰当速度的第四分量,c 是真空光速。也许,我们会觉得很奇怪,为什么快度这么复杂的概念反而是一个好的物理量呢?这与我们看问题的角度有关,在狭义相对论的时空观看来,快度是衡量物体运动快慢最自然的物理量。因为它就是时空转动的转角(如果我们把 Lorentz boost 想象成一种旋转的话),从某种意义上,我们可以认为快度衡量了世界线和时间轴的“夹角”。对于静止的物体,世界线沿时间轴方向,夹角为0,所以快度也为0,故称之为静止。对于光来说,比较奇特一些,因为时空是 Minkowski 空间,所以夹角这件事情不是我们直接用量角器可以量出来的。实际上,按照定义式计算,光的快度是无穷大。
光的快度是无穷大,这说明了两个问题:第一,没有任何物体的快度可以比光更大,所以光是最快的;第二,无穷大加减任何有限的快度,仍然是无穷大,所以光在任何有限快度的参考系中,都是无穷快的,也就是说,光速不变。
复制的豆瓣的Everett的回答
srtwin 双胞胎 固有时t类似于普通空间中弧长s的概念。在普通空间中,弧长s表示一条曲线的长度,或者说是一个人走过的路径的长度
固有时t类似于普通空间中弧长s的概念。在普通空间中,弧长s表示一条曲线的长度,或者说是一个人走过的路径的长度
固有时用以描述时空中两个事件之间流过的时间,这个时间被赋予事件自身的时钟所测量。因而,测量结果不仅取决于两个事件对应的时空点位置,而且也取决于时钟参与其中的具体过程。再表达得更简要一点,固有时是时钟的世界线长度
实际上,我们之前学过了黎曼几何,对固有时的概念不难理解,它就是对应于在黎曼几何中经常强调的内蕴几何不变量:弧长s。对广义相对论重要的内蕴性质,在狭义相对论中也很重要。
如何来计算两个双胞胎在重逢时各自度过的真实年龄呢?结论是:计算和比较他们在两次相遇之间的固有时。因为固有时t是内蕴不变的,这个计算可以在任何一个参考系中进行,都将得到同样的结果。每个人的年龄是由他身体的新陈代谢机制决定的,他的身体内有一个生物钟。人体处于各种运动状态(静止或运动、加速或减速)时,他的生物钟便会随着变化,或减慢,或加快,这便可以作为每个人自己带着的“时钟”。下面,我们首先用地球参考系来考察两个双胞胎在两次相遇之间的固有时。刘地一直停留在地球上没有移动,他的世界线是地球参考系中时间轴上的一段,这个参考系中,他的固有时也就等于坐标时,等于60年。而刘天的世界线是图2-12-2c右图中的OBD折线。折线中每一段的长度是20年,两段相加等于40年。所以,两个双生子在D点见面的时候,刘天40岁、刘地60岁。
表達了移動時鐘的周期比參考系的時鐘要慢這個事實
移動時鐘的周期比參考系的時鐘要慢這個事實。
"想象一個由兩面鏡子A和B組成的時鐘,兩面鏡子相距L,其間有光束來回反射,光束每次接觸到其中一面鏡子時,時鐘便會走動"
周期:
想象一個由兩面鏡子A和B組成的時鐘,兩面鏡子相距L,其間有光束來回反射,光束每次接觸到其中一面鏡子時,時鐘便會走動
時間膨脹[编辑]
時間膨脹是一種物理現象:兩個完全相同的時鐘之中,拿著甲鐘的人會發現乙鐘比自己的走得慢。這現象常被說為是對方的鐘“慢了下來”,但這種描述只會在觀測者的參考系上才是正確的。任何本地的時間(也就是位于同一個座標系上的觀測者所測量出的時間)都以同一個速度前進。時間膨脹效應適用于任何解釋時間速度變化的過程。
在阿爾伯特·愛因斯坦的相對論中,時間膨脹出現于兩种狀況:
狹義相對論中,時間膨脹效應是相互性的:從任一個時鐘觀測,都是對方的時鐘走慢了(當然我們假定兩者相互的運動的等速均勻的,兩者在觀測對方時都沒有加速度)。
相反,引力時間膨脹卻不是相互性的:塔頂的觀測者覺得地面的時鐘走慢了,而地面的觀測者覺得塔頂的時鐘走快了。引力時間膨脹效應對於每個觀測者都是一樣的,膨脹與引力場的強弱與觀察者所處的位置都有關係。
因為勞侖茲因子而引起的時間膨脹現象是於1897年由Joseph Larmor發現──最起碼有電子在原子核運轉而引起的現象。
人們更加有可能利用這個效應把人類送到距離我們最近的恆星上,而不需耗掉航天員的一生光陰。然而,要實現這種省時的情況,我們則需要研發一些更新、更先進的推進技術。另一個問題是,在這麽高的速度下,空間裏的粒子會折射,成爲高能量的宇宙射線。要想飛船不被毀滅,我們必須用到一些不可思議的防輻射措施。其中一種建議的措施是利用強電磁場把前來的物質離子化,或把它們反出去。
目前的航天科技有著許多根本性的限制,如要把飛船加速到接近光速需要大量能量,小型碎片等會對飛船造成威脅。不過,在今天的航天任務中,時間膨脹並不是考慮的因素之一,因爲就算是頂速也達不到有效的速度。另外一個太空飛行會涉及到的時間膨脹效應情況,是接近一個有著極大引力的地方,如黑洞,那裏會有強大的引力時間膨脹效應。
設t為一慣性系統的時間。設x為空間座標,並設x軸平行于飛船固定加速的路徑。假設飛船的位置是t = 0、x = 0,而其速度為v0,以下的公式有[1]:
位置::
想象一個由兩面鏡子A和B組成的時鐘,兩面鏡子相距L,其間有光束來回反射,光束每次接觸到其中一面鏡子時,時鐘便會走動。
參考系靜止時(右上圖),光來回一次的路徑長度為2L,時鐘走過的時間為2L除以光速:
光束走過其路徑的總時間為
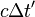
日常生活中其實也有這種怪異的情況:如果兩人相距一段距離,則A會看到B“縮小”了,但是B也覺得A“縮小”了。這種透視現象已經被人們適應、接受了,因爲它存在于平日的生活裏,但是人們對相對論就毫無準備。
我們已經對有關距離的相對論見解習以爲常了:從北京到上海的距離當然等於上海到北京的距離。另一方面,當我們考慮到速度方面,會認爲如果一個物體在運動,運動一定會是相對于某物:星體、地面或另一人。A物相對B物的速度,是相等于B物相對A物的速度,兩者完全相等。
在狹義相對論中,一個移動中的時鐘相對觀測者的時鐘顯得較慢。如果A和B在不同的飛船上,而相對速度為接近光速,則A(使用自己的時鐘)覺得B時間變慢了,B也覺得A的時間慢了。
注意要在參考系統中建立“同步”的概念,“到底一件事是否和另一處的另一件事同時發生”這個問題有著關鍵的重要性。所有計算都最終要涉及到哪些事件是同時發生的。也要留意,要建立兩個空間中相隔的事件的同步性,這兩個地方一定要有訊息相互傳遞,這也代表了光速是決定同步性的一個重要因素。
大家當然會問到,狹義相對論怎麽能在A相對B有時間膨脹而B相對A也有時間膨脹的情況下不前後矛盾。要消除矛盾,我們必須丟棄人們日常對同步性的直覺概念。同步性,是位于一個參考系中的一位觀測者和一系列事件之間的關係。如此類推,我們能接受“左”和“右”是參照于觀測者的位置和方向。這是因爲左和右是一種物體間的關係。同理,柏拉圖解釋,“上”和“下”是對應于地球的表面的一種關係,因此人們是不會在他們的對蹠地掉下去。
理論的架構裏有一個同時性的相對論,它影響著特定事件如何根據有相對運動的觀測者被調准。由於每個觀測者對兩個事件是否同時發生都有不同的見解(見孿生子佯謬),因此任一個觀測者都可認爲對方的時鐘減慢了,這並不會導致理論自相矛盾。這矛盾現象有許多更明確的解釋,如下。
一位觀測者發送一束光訊息,根據他的時鐘時間為t1。在一處遙遠的事件,這束光被反射回來,在t2時到達原先的觀測者(根據同一個時鐘測量)。這個情況下,由於光線來回都以同一個速度走著同一條路線,因此光訊息在遙遠處被彈回來的那一刻的時間tE為tE = (t1 + t2) / 2。這樣,使用一個觀測者的一個時鐘便可以定義時態座標系,並在宇宙各處都適用。
對稱的時間膨脹效應發于以這種方式設立的時態座標系中。效應中,另一個時鐘被觀測者認爲走慢了。觀測者並不覺得自己身上發生著時間膨脹,但他可以知道相對另一個座標系,他的時間是顯得較慢。
藍點代表光束。根據綠色船隊的時間,光束每來回一次所花時間為2秒,單向所需時間為1秒。
從紅色飛船看(根據自己的時間),兩個紅色飛船之間的光束單向所需時間為1秒。而從綠色飛船來看,紅色飛船之間所發出光線的路徑為一個對角的斜線,單向所需時間為2秒。(以綠色的角度看,紅色飛船每2秒(綠色飛船時間)行進距離為1.73( )光秒。)
)光秒。)
其中一艘紅色飛船每秒向綠船發射訊號。根據綠色飛船的時間,每隔2秒才接收一次訊號。動畫中沒有提到的是,所有物理效應都被等比例縮小了。紅色飛船發出的訊號頻率(紅色飛船所測量到的)比綠色飛船接收到的訊號頻率(綠色飛船所測量到的)要高,反之亦然。
此動畫分別以紅色或綠色飛船作爲參考物,藉以強調速度時間膨脹的對稱性質。由於相對論中(牛頓力學中也如此)沒有絕對運動這回事,因此無論是紅色還是綠色的船隊“在其自己的參考系中”都會認爲自己是不動的。
每个函数都依赖于固有时。 时间膨胀从时间膨... ... 界线定义为其中是固有时。 四维速度的分量时... ... 坐标间的关系为对固有时求导数, 我们得到四维... 参考系拖拽.
△t0是本征时间或固有时. 时间膨胀了, 系观测时, 时间膨胀了,即S系观测时, 过程变慢了. 过程变慢了. ux′ t′ + 2 c t= 1.为什么用2 1 β 讨论: 讨论: 用u t 2 (x2 x1) c t′
固有时用以描述时空中两个事件之间流过的时间,这个时间被赋予事件自身的时钟所测量。因而,测量结果不仅取决于两个事件对应的时空点位置,而且也取决于时钟参与其中的具体过程。再表达得更简要一点,固有时是时钟的世界线长度
实际上,我们之前学过了黎曼几何,对固有时的概念不难理解,它就是对应于在黎曼几何中经常强调的内蕴几何不变量:弧长s。对广义相对论重要的内蕴性质,在狭义相对论中也很重要。
如何来计算两个双胞胎在重逢时各自度过的真实年龄呢?结论是:计算和比较他们在两次相遇之间的固有时。因为固有时t是内蕴不变的,这个计算可以在任何一个参考系中进行,都将得到同样的结果。每个人的年龄是由他身体的新陈代谢机制决定的,他的身体内有一个生物钟。人体处于各种运动状态(静止或运动、加速或减速)时,他的生物钟便会随着变化,或减慢,或加快,这便可以作为每个人自己带着的“时钟”。下面,我们首先用地球参考系来考察两个双胞胎在两次相遇之间的固有时。刘地一直停留在地球上没有移动,他的世界线是地球参考系中时间轴上的一段,这个参考系中,他的固有时也就等于坐标时,等于60年。而刘天的世界线是图2-12-2c右图中的OBD折线。折线中每一段的长度是20年,两段相加等于40年。所以,两个双生子在D点见面的时候,刘天40岁、刘地60岁。
表達了移動時鐘的周期比參考系的時鐘要慢這個事實
移動時鐘的周期比參考系的時鐘要慢這個事實。
"想象一個由兩面鏡子A和B組成的時鐘,兩面鏡子相距L,其間有光束來回反射,光束每次接觸到其中一面鏡子時,時鐘便會走動"
周期:
時間膨脹的簡單推論[编辑]
由於光在任何參照系中的速度都相同,於是時間膨脹可以解釋為下:想象一個由兩面鏡子A和B組成的時鐘,兩面鏡子相距L,其間有光束來回反射,光束每次接觸到其中一面鏡子時,時鐘便會走動
時間膨脹[编辑]
维基百科,自由的百科全书
在阿爾伯特·愛因斯坦的相對論中,時間膨脹出現于兩种狀況:
狹義相對論中,時間膨脹效應是相互性的:從任一個時鐘觀測,都是對方的時鐘走慢了(當然我們假定兩者相互的運動的等速均勻的,兩者在觀測對方時都沒有加速度)。
相反,引力時間膨脹卻不是相互性的:塔頂的觀測者覺得地面的時鐘走慢了,而地面的觀測者覺得塔頂的時鐘走快了。引力時間膨脹效應對於每個觀測者都是一樣的,膨脹與引力場的強弱與觀察者所處的位置都有關係。
目录
[隐藏]概述[编辑]
狹義相對論中測定時間膨脹的公式為: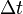 是根據某個觀測者的時鐘,兩個本地事件(就是在同地方發生的兩個事件)之間的時間間隔——這被稱爲原時;
是根據某個觀測者的時鐘,兩個本地事件(就是在同地方發生的兩個事件)之間的時間間隔——這被稱爲原時; 是根據另一個觀測者的時鐘,同兩個事件之間的時間間隔;
是根據另一個觀測者的時鐘,同兩個事件之間的時間間隔; 是第二個時鐘相對第一個時鐘移動的速度;
是第二個時鐘相對第一個時鐘移動的速度; 是光速;而
是光速;而 是勞侖茲因子。
是勞侖茲因子。
因為勞侖茲因子而引起的時間膨脹現象是於1897年由Joseph Larmor發現──最起碼有電子在原子核運轉而引起的現象。
實驗證明[编辑]
時間膨脹的試驗已經做過許多次了。自1950年代開始的粒子加速器(如歐洲核子研究組織的加速器)的日常工作,就是持續進行的狹義相對論實驗。具體的幾個實驗包括:速度時間膨脹實驗[编辑]
- Rossi and Hall(1941)比較了位于山頂和位于海平面的由宇宙射線製造出的緲子數量。儘管緲子從山頂到地面所需的時間已經是幾個半衰期,但是在海面的緲子數量卻只是少了一點。這是由於緲子相對于測試者以高速運動,導致了可觀的時間膨脹效應。經計算,快速移動的緲子的衰變速度比它們相對測試者靜止時的衰變速度要慢10倍。
引力時間膨脹實驗[编辑]
- Pound, Rebka在1959年測量出位于較低海拔(所受重力較強)的光波的頻率有很小的引力紅移。得出的數值和廣義相對論預測的數值有小於10%的偏差。不久后Pound和Snider在1964年得出更准的1%偏差,正好就是引力時間膨脹預測的效應。
速度和引力時間膨脹結合實驗[编辑]
- Hafele and Keating在1971年把兩個銫原子鐘分別放在兩架分別向東和西飛的商務客機上,並對比放在美國海軍天文臺的時鐘。飛機上的原子鐘應該衰變得更快,因爲他們位于距離地面較高,因此引力時間膨脹較小。不過,相反地,它們又會走得較慢,因爲他們相對天文臺的時鐘的速度很快。而當中的引力時間膨脹效應較大,因此兩個時鐘的時間相對走快了。實驗結果和預測的結果相符合。在2005年,英國國家物理實驗室公佈了他們在另一次相似的實驗中所得出的結果。[1]這次實驗的飛行時間較1971年的那一次短(來回倫敦和華盛頓),但是實驗之中的原子鐘更爲精確。公佈的結果誤差為4%。
- 全球定位系統可被視爲一項持續進行的狹義和廣義相對論實驗。軌道上的時鐘根據時間膨脹效應被調校成適當的速度,以對應位于地面的時鐘。另外,有關廣義相對論的一些微調已經編寫進定位衛星,要不然,每12個小時定位結果便會有大約7米的偏差。[來源請求]
介子衰期[编辑]
比較不同速度下μ-介子的衰期是可行的。慢速的介子可在實驗室裏製造,而快速的介子則在宇宙射線穿入大氣層時製造出來。實驗室中靜止介子的衰期為2.22 μs,由宇宙射線製造出來的介子的速度為光速的98%,衰期為比靜止時大5倍左右,和理論相符合。[2]實驗中的“時鐘”是介子的衰期,而高速運動介子的時鐘有著自己的前進速度,也就是比實驗室裏的“時鐘”慢許多。太空飛行與時間膨脹[编辑]
有了時間膨脹效應,人們在以極高速運動的飛船時,儘管外界已經經歷了很長的歲月,自己卻沒什麽老化,因爲極大的速度會使飛船(和裏面的所有物體)的時間減慢。也就是說,飛船的時鐘走了一圈,地球上的時鐘已經轉了許多圈了。只要速度夠高,這個效應便會明顯地顯示出來。比方説,旅行者似乎只航行了一年,對地球上的人來説卻有十年之久。實際上,只要以地球引力加速度(9.80665 m/s2)行進,旅行者在有生之年完成的旅行距離為光從大爆炸起到現在走過的距離,也就是137億光年之遠!這個旅行者回到地球后,地球已經經過了數十億年了。這個題材被用於Pierre Boulle的長篇小説《人猿星球》中。人們更加有可能利用這個效應把人類送到距離我們最近的恆星上,而不需耗掉航天員的一生光陰。然而,要實現這種省時的情況,我們則需要研發一些更新、更先進的推進技術。另一個問題是,在這麽高的速度下,空間裏的粒子會折射,成爲高能量的宇宙射線。要想飛船不被毀滅,我們必須用到一些不可思議的防輻射措施。其中一種建議的措施是利用強電磁場把前來的物質離子化,或把它們反出去。
目前的航天科技有著許多根本性的限制,如要把飛船加速到接近光速需要大量能量,小型碎片等會對飛船造成威脅。不過,在今天的航天任務中,時間膨脹並不是考慮的因素之一,因爲就算是頂速也達不到有效的速度。另外一個太空飛行會涉及到的時間膨脹效應情況,是接近一個有著極大引力的地方,如黑洞,那裏會有強大的引力時間膨脹效應。
以固定加速度前進時的時間膨脹[编辑]
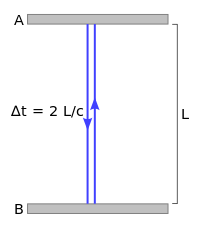
在狹義相對論中,時間膨脹絕大多數時候都出現在相對運動速度不變的情況下。不過,勞侖茲公式允許我們算出兩物之間有固定加速度時的時間膨脹,就是一物相對另一個沒有加速度的物體以g速固定地加速。設t為一慣性系統的時間。設x為空間座標,並設x軸平行于飛船固定加速的路徑。假設飛船的位置是t = 0、x = 0,而其速度為v0,以下的公式有[1]:
位置::
時間膨脹的簡單推論[编辑]
由於光在任何參照系中的速度都相同,於是時間膨脹可以解釋為下:想象一個由兩面鏡子A和B組成的時鐘,兩面鏡子相距L,其間有光束來回反射,光束每次接觸到其中一面鏡子時,時鐘便會走動。
參考系靜止時(右上圖),光來回一次的路徑長度為2L,時鐘走過的時間為2L除以光速:
光束走過其路徑的總時間為
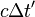
時間膨脹在兩個慣性觀測者之間是對稱的[编辑]
常理會認爲,如果飛船裏的時間被拖慢了,則裏面的航天員會看到外面的世界相對地“加速”了。可是,狹義相對論卻算出相反的結果。日常生活中其實也有這種怪異的情況:如果兩人相距一段距離,則A會看到B“縮小”了,但是B也覺得A“縮小”了。這種透視現象已經被人們適應、接受了,因爲它存在于平日的生活裏,但是人們對相對論就毫無準備。
我們已經對有關距離的相對論見解習以爲常了:從北京到上海的距離當然等於上海到北京的距離。另一方面,當我們考慮到速度方面,會認爲如果一個物體在運動,運動一定會是相對于某物:星體、地面或另一人。A物相對B物的速度,是相等于B物相對A物的速度,兩者完全相等。
在狹義相對論中,一個移動中的時鐘相對觀測者的時鐘顯得較慢。如果A和B在不同的飛船上,而相對速度為接近光速,則A(使用自己的時鐘)覺得B時間變慢了,B也覺得A的時間慢了。
注意要在參考系統中建立“同步”的概念,“到底一件事是否和另一處的另一件事同時發生”這個問題有著關鍵的重要性。所有計算都最終要涉及到哪些事件是同時發生的。也要留意,要建立兩個空間中相隔的事件的同步性,這兩個地方一定要有訊息相互傳遞,這也代表了光速是決定同步性的一個重要因素。
大家當然會問到,狹義相對論怎麽能在A相對B有時間膨脹而B相對A也有時間膨脹的情況下不前後矛盾。要消除矛盾,我們必須丟棄人們日常對同步性的直覺概念。同步性,是位于一個參考系中的一位觀測者和一系列事件之間的關係。如此類推,我們能接受“左”和“右”是參照于觀測者的位置和方向。這是因爲左和右是一種物體間的關係。同理,柏拉圖解釋,“上”和“下”是對應于地球的表面的一種關係,因此人們是不會在他們的對蹠地掉下去。
理論的架構裏有一個同時性的相對論,它影響著特定事件如何根據有相對運動的觀測者被調准。由於每個觀測者對兩個事件是否同時發生都有不同的見解(見孿生子佯謬),因此任一個觀測者都可認爲對方的時鐘減慢了,這並不會導致理論自相矛盾。這矛盾現象有許多更明確的解釋,如下。
時態座標系與時鐘同步[编辑]
相對論使用時鐘同步的步驟來建立時態座標系。現在這常被稱爲愛因斯坦同步步驟,因爲曾出現在他于1905年的論文裏。一位觀測者發送一束光訊息,根據他的時鐘時間為t1。在一處遙遠的事件,這束光被反射回來,在t2時到達原先的觀測者(根據同一個時鐘測量)。這個情況下,由於光線來回都以同一個速度走著同一條路線,因此光訊息在遙遠處被彈回來的那一刻的時間tE為tE = (t1 + t2) / 2。這樣,使用一個觀測者的一個時鐘便可以定義時態座標系,並在宇宙各處都適用。
對稱的時間膨脹效應發于以這種方式設立的時態座標系中。效應中,另一個時鐘被觀測者認爲走慢了。觀測者並不覺得自己身上發生著時間膨脹,但他可以知道相對另一個座標系,他的時間是顯得較慢。
速度時間膨脹的時空幾何[编辑]
動畫中的綠點和紅點代表飛船。綠色船隊相互並沒有速度,因此每艘飛船上的時鐘所走的速度都相同,而船隊則可以保持飛船之間的同步。紅色船隊相對綠色船隊移動,速度是光速的0.866倍。藍點代表光束。根據綠色船隊的時間,光束每來回一次所花時間為2秒,單向所需時間為1秒。
從紅色飛船看(根據自己的時間),兩個紅色飛船之間的光束單向所需時間為1秒。而從綠色飛船來看,紅色飛船之間所發出光線的路徑為一個對角的斜線,單向所需時間為2秒。(以綠色的角度看,紅色飛船每2秒(綠色飛船時間)行進距離為1.73(
 )光秒。)
)光秒。)其中一艘紅色飛船每秒向綠船發射訊號。根據綠色飛船的時間,每隔2秒才接收一次訊號。動畫中沒有提到的是,所有物理效應都被等比例縮小了。紅色飛船發出的訊號頻率(紅色飛船所測量到的)比綠色飛船接收到的訊號頻率(綠色飛船所測量到的)要高,反之亦然。
此動畫分別以紅色或綠色飛船作爲參考物,藉以強調速度時間膨脹的對稱性質。由於相對論中(牛頓力學中也如此)沒有絕對運動這回事,因此無論是紅色還是綠色的船隊“在其自己的參考系中”都會認爲自己是不動的。
固有时: definition of 固有时and synonyms of 固有时(Chinese)
dictionary.sensagent.com/固有时/zh-zh/
轉為繁體網頁
轉為繁體網頁
相对论课件_百度文库
220.181.112.102/view/2b267ceef8c75fbfc77db23f.html
轉為繁體網頁
轉為繁體網頁
那个负号直接对应于时间的物理在于,对于欧式时空,没有天然的过去未来之分,而对于闵氏时空,如 那个负号直接对应于时间的物理在于,对于欧式时空,没有天然的过去未来之分,而对于闵氏时空,如果事件A和事件B有一个类时的时间间隔s,那么在A的眼里,事件B可以在一个双支双曲面上面,这两支的区分使得从几何上我们可以定义一支为过去,一支为将来。而欧式时空,同样的考虑,事件B在一个球面上,从几何上我们无法定义过去、将来,因果律只能手加上去、时空没有蕴含这样的信息(至少部分蕴含)。 ... K
其实你说的差不多,其根本原因应该就是一些“时间”维度与“空间三维”不同的性质所导致的差异
譬如无论是从“时间单一,不可逆的方向性”而言,还是从其“因果性”约束来说,“时间的正方向”应该是:无论从哪个参考系观察,都是绝不停留的从“过去”,经由“现在此时此刻”,向“未来”无限延伸, 而不会反其道而行之的从“此时此刻”向“过去”回溯。
而无论我们是否意识的到,其实当我们在闵可夫四维时空坐标系中定位了一个点的时候,实际上也就同时代表了一件事:这个事件,要么“已经发生”,要么“正在发生”,而不可能是“尚未发生”,因为如果是“尚未发生”的事件,是不存在“可确定性”的,所以也就不可能“确定”其在空间中的确切位置,而一旦能够“确定”了,那么也代表着这个事件“已经发生”或者“正在发生”。
同样,如上所述,一个向未来不断延伸,绝不停留的“正方向时间”,它必定是无法度量的,换句话说,只要我们能够去度量一段“时间的长度”,那么我们所能度量的就必然只可能是那些“已经发生了的时间长度”,因之未来不可度量,无限延伸....
除此以外,“时间”的上述特性必然也将不会因为开平方这样的数学处理而改变或者消失泯灭。
那么,为什么会引入“虚数”的原因说到这里大概也就呼之欲出了吧?
所以,闵可夫斯基当初是“有意而为之”的~并且这其中所蕴含的道理,也绝非是“脱离了搬书学舌,以及令人眼花缭乱的公式与数学游戏”就说不清的,更不是米兰时装周,看哪种“更时髦”~
或者更进一步说,有没有一种可能,要理解为什么在闵可夫斯基时空模型中,“时间”这一维的表述中 或者更进一步说,有没有一种可能,要理解为什么在闵可夫斯基时空模型中,“时间”这一维的表述中与众不同的引入了"虚数”的概念,实际并不一定非要张口闭口引用那些看似令人眼花缭乱的数学公式,而实际说到底是因为“时间”这一维是有着一些与“空间”那三维完全不一样的独特性质?比如某种“单一不可逆的方向性”以及“分分秒秒流逝而绝不停留的运动性”? 是否恰恰是因为“时间”这一维度上所存在的一些特殊性质,才使得其在公式中的表述上与“空间”那三维相比,显得“很不一样”? ... Neo
那个负号直接对应于时间的物理在于,对于欧式时空,没有天然的过去未来之分,而对于闵氏时空,如果事件A和事件B有一个类时的时间间隔s,那么在A的眼里,事件B可以在一个双支双曲面上面,这两支的区分使得从几何上我们可以定义一支为过去,一支为将来。而欧式时空,同样的考虑,事件B在一个球面上,从几何上我们无法定义过去、将来,因果律只能手加上去、时空没有蕴含这样的信息(至少部分蕴含)。
也说点四维时空
其实你说的差不多,其根本原因应该就是一些“时间”维度与“空间三维”不同的性质所导致的差异
譬如无论是从“时间单一,不可逆的方向性”而言,还是从其“因果性”约束来说,“时间的正方向”应该是:无论从哪个参考系观察,都是绝不停留的从“过去”,经由“现在此时此刻”,向“未来”无限延伸, 而不会反其道而行之的从“此时此刻”向“过去”回溯。
而无论我们是否意识的到,其实当我们在闵可夫四维时空坐标系中定位了一个点的时候,实际上也就同时代表了一件事:这个事件,要么“已经发生”,要么“正在发生”,而不可能是“尚未发生”,因为如果是“尚未发生”的事件,是不存在“可确定性”的,所以也就不可能“确定”其在空间中的确切位置,而一旦能够“确定”了,那么也代表着这个事件“已经发生”或者“正在发生”。
同样,如上所述,一个向未来不断延伸,绝不停留的“正方向时间”,它必定是无法度量的,换句话说,只要我们能够去度量一段“时间的长度”,那么我们所能度量的就必然只可能是那些“已经发生了的时间长度”,因之未来不可度量,无限延伸....
除此以外,“时间”的上述特性必然也将不会因为开平方这样的数学处理而改变或者消失泯灭。
那么,为什么会引入“虚数”的原因说到这里大概也就呼之欲出了吧?
所以,闵可夫斯基当初是“有意而为之”的~并且这其中所蕴含的道理,也绝非是“脱离了搬书学舌,以及令人眼花缭乱的公式与数学游戏”就说不清的,更不是米兰时装周,看哪种“更时髦”~
或者更进一步说,有没有一种可能,要理解为什么在闵可夫斯基时空模型中,“时间”这一维的表述中 或者更进一步说,有没有一种可能,要理解为什么在闵可夫斯基时空模型中,“时间”这一维的表述中与众不同的引入了"虚数”的概念,实际并不一定非要张口闭口引用那些看似令人眼花缭乱的数学公式,而实际说到底是因为“时间”这一维是有着一些与“空间”那三维完全不一样的独特性质?比如某种“单一不可逆的方向性”以及“分分秒秒流逝而绝不停留的运动性”? 是否恰恰是因为“时间”这一维度上所存在的一些特殊性质,才使得其在公式中的表述上与“空间”那三维相比,显得“很不一样”? ... Neo
那个负号直接对应于时间的物理在于,对于欧式时空,没有天然的过去未来之分,而对于闵氏时空,如果事件A和事件B有一个类时的时间间隔s,那么在A的眼里,事件B可以在一个双支双曲面上面,这两支的区分使得从几何上我们可以定义一支为过去,一支为将来。而欧式时空,同样的考虑,事件B在一个球面上,从几何上我们无法定义过去、将来,因果律只能手加上去、时空没有蕴含这样的信息(至少部分蕴含)。
也说点四维时空
希望通过本文能廓清一些被混淆的概念。
按照狭义相对论的说法,四维时空是我们描述惯性参照系的一种手段,注意,仅仅是一种手段,既不是唯一手段,也说不定将来会有更好的手段--但是目前来看是最好的手段。
所谓惯性参照系,是那些牛顿第一定律成立的参照系。牛顿第一定律说:“一个物体总是保持静止或匀速直线运动,直到外力迫使它改变这个状态为止。”
严格的惯性参照系是不存在的。也就是牛顿第一定律其实在任何参照系中仅仅近似成立。
比如地球表面可以看成是相当好的惯性参照系。然而学过高中地理的同学都知道一个东西叫地转偏向力(物理学上叫科里奥列力),这个东西产生的根源就是因为地球表面参照系不是惯性系--无匹并没有受到让它转向的力,它却转向了(季风,洋流等等)。
在爱因斯坦之前,人们也用四维时空描述惯性参照系:任何物理事件都是由三维空间坐标和一维时间坐标描述的。只不过在那个年代大家认为这一维时间和那三维空间是无关的。时间是一个外在的变量。大家认为在两个不相对静止的惯性参照系之间的坐标变换之涉及空间坐标的变换而时间坐标对于各个(惯性)参照系都是一样的。在经典力学时空观里,在参照系变换下两个物理事件的空间距离和时间距离都是不变的。举个例子,“王尼玛在2014年4月11日0:00于金茂大厦顶层第二个水箱下被菊爆”,和“唐马儒于2014年4月1日1:00在天安门广场旗杆下干了一碗热翔”这两件事情,不论在哪个参照系来看,时间距离都是一个小时,空间距离都是1080km左右。
直到爱因斯坦发现,这个时间坐标对于各个(惯性)参照系其实是不同的。它也会参与参照系变换。所以在某个GPS定位卫星上,看到唐马儒干翔和王尼玛被菊爆可能时间差距就不再是一个小时而空间距离也不再是1080km了。爱因斯坦进一步发现,两间事情的(时间距离乘以光速)的平方减去(空间距离)的平方是个定值,在任何一个惯性参照系中看都一样。于是老爱用了一个奇怪的叫做四维闵可夫斯基空间的数学对象来刻画这件事情,这只是一种刻画,当然有别的刻画方法。只不过老爱当年翘的数学课太多(他的数学老师就是闵可夫斯基,而老闵甚至都不记得他有个学生叫爱因斯坦),于是他只能想出这个办法。我们后代的数学家和物理学家更懒,就沿用了老爱当年的方法。
这就是所谓四维时空的由来。四维时空和四维空间是完全不同的两个概念。谈论之前要先分清这两点。四维时空是四维闵可夫斯基空间,而四维空间的装逼数学名称叫做四维欧几里德空间(对,就是编初中平面几何教科书的那个古希腊老爷爷欧几里德)这俩货完全不同。说简单点,四维闵可夫斯基空间上两个点(对应两个物理事件)的距离是两个事件的(时间坐标差乘以光速)的平方减去(空间距离)的平方再开平方根。而四维欧几里德空间上两个点的距离是四个坐标差的平方求和再开平方根。
噗~先写这么多……
按照狭义相对论的说法,四维时空是我们描述惯性参照系的一种手段,注意,仅仅是一种手段,既不是唯一手段,也说不定将来会有更好的手段--但是目前来看是最好的手段。
所谓惯性参照系,是那些牛顿第一定律成立的参照系。牛顿第一定律说:“一个物体总是保持静止或匀速直线运动,直到外力迫使它改变这个状态为止。”
严格的惯性参照系是不存在的。也就是牛顿第一定律其实在任何参照系中仅仅近似成立。
比如地球表面可以看成是相当好的惯性参照系。然而学过高中地理的同学都知道一个东西叫地转偏向力(物理学上叫科里奥列力),这个东西产生的根源就是因为地球表面参照系不是惯性系--无匹并没有受到让它转向的力,它却转向了(季风,洋流等等)。
在爱因斯坦之前,人们也用四维时空描述惯性参照系:任何物理事件都是由三维空间坐标和一维时间坐标描述的。只不过在那个年代大家认为这一维时间和那三维空间是无关的。时间是一个外在的变量。大家认为在两个不相对静止的惯性参照系之间的坐标变换之涉及空间坐标的变换而时间坐标对于各个(惯性)参照系都是一样的。在经典力学时空观里,在参照系变换下两个物理事件的空间距离和时间距离都是不变的。举个例子,“王尼玛在2014年4月11日0:00于金茂大厦顶层第二个水箱下被菊爆”,和“唐马儒于2014年4月1日1:00在天安门广场旗杆下干了一碗热翔”这两件事情,不论在哪个参照系来看,时间距离都是一个小时,空间距离都是1080km左右。
直到爱因斯坦发现,这个时间坐标对于各个(惯性)参照系其实是不同的。它也会参与参照系变换。所以在某个GPS定位卫星上,看到唐马儒干翔和王尼玛被菊爆可能时间差距就不再是一个小时而空间距离也不再是1080km了。爱因斯坦进一步发现,两间事情的(时间距离乘以光速)的平方减去(空间距离)的平方是个定值,在任何一个惯性参照系中看都一样。于是老爱用了一个奇怪的叫做四维闵可夫斯基空间的数学对象来刻画这件事情,这只是一种刻画,当然有别的刻画方法。只不过老爱当年翘的数学课太多(他的数学老师就是闵可夫斯基,而老闵甚至都不记得他有个学生叫爱因斯坦),于是他只能想出这个办法。我们后代的数学家和物理学家更懒,就沿用了老爱当年的方法。
这就是所谓四维时空的由来。四维时空和四维空间是完全不同的两个概念。谈论之前要先分清这两点。四维时空是四维闵可夫斯基空间,而四维空间的装逼数学名称叫做四维欧几里德空间(对,就是编初中平面几何教科书的那个古希腊老爷爷欧几里德)这俩货完全不同。说简单点,四维闵可夫斯基空间上两个点(对应两个物理事件)的距离是两个事件的(时间坐标差乘以光速)的平方减去(空间距离)的平方再开平方根。而四维欧几里德空间上两个点的距离是四个坐标差的平方求和再开平方根。
噗~先写这么多……
评论 (6) 只看楼主
全部评论
-
2014-04-11 05:12 胖大叔_tschao 只看Ta
“四维时空是四维闵可夫斯基空间,而四维空间的装逼数学名称叫做四维欧几里德空间(对,就是编初中平面几何教科书的那个古希腊老爷爷欧几里德)这俩货完全不同。说简单点,四维闵可夫斯基空间上两个点(对应两个物理事件)的距离是两个事件的(时间坐标差乘以光速)的平方减去(空间距离)的平方再开平方根。而四维欧几里德空间上两个点的距离是四个坐标差的平方求和再开平方根。”[0] |
嗯。这段话完全可以当作绕口令。学播音的家伙们有福了,谁让你们嘲笑理科生,上课不认真的?下回考试题就是它了。 -
2014-04-11 06:06 泡泡们的熊国 只看Ta
那继续啦……[0] |
既然上面一节说到,彻底的精确的惯性参照系是不存在的,那么貌似我们讨论的惯性参照系之间的变换貌似是没有意义的。然而嘛,物理学的理论就是这样——从来就没有精确东西,全是近似的。
一些经典的试验已经证实了爱因斯坦关于两个惯性参照系之间的的变换规则了。比如有一种不稳定的粒子叫\mu子。每过一段时间(我忘了多长时间了)它就会有50%的概率衰变成别的粒子——也就是说比如你拿1000个\mu粒子,过这么长时间就剩下一半了。再过这么长时间就只剩下四分之一了(这叫半衰期~)。当然粒子物理学家们测量这个时间的时候是在实验室里测量的静止的\mu粒子。之后有个哥们儿头脑风暴了一下说咱们测测宇宙射线里来的高速\mu粒子的半衰期吧!(其实貌似也不是宇宙射线里的,而是宇宙射线轰击空气里面的不知道什么分子产生的次级产物)。然后他们测到一\mu子从产生到衰变走过一段长得离奇的路径!按照它那么短的寿命根本不应该能存活这么长时间以至于走过这么长的距离!
然而爱因斯坦同学有解释:你不是测量的高速飞行的粒子么?在它自己看来,它的确只活了一丢丢的时间,而且在它自己看来,它从出生到衰变就没挪地方(空间距离是零)。然而,在实验室的物理学家看来,它从出生到衰变之间有个空间距离。然后引用老爱同学的发现,出生到衰变这两件物理事件,在不同的参照系看来时间间隔和空间间隔都可以不同,但是两者的平方差是不变的。于是,因为物理学家看到了粒子产生和衰变不在一个地方于是空间间隔不是零,从而在物理学家看来时间间隔比在粒子自己看来时间间隔要大。于是在物理学家看来,粒子就有了足够长的时间走过这么长的距离~
-
2014-04-11 06:12 泡泡们的熊国 只看Ta
以上的讨论都是关于狭义相对论的,也就是只考虑运动状态对于时间可空间的影响——也可以说只考虑真空状态下时空的性质。爱因斯坦同学的狭义相对论用一句话概括就是:[0] |
两个物理事件在不同的观察者看来,时间间隔和空间间隔都可以不同(在以前我们认为这两者都是不变的)然而(时间间隔乘以光速)的平方减去(空间间隔)的平方却在任何观察者看来都是一样的(前提是这些观察者之间保持匀速直线运动)。
然后我们进入广义相对论的讨论~ -
2014-04-11 19:40 泡泡们的熊国 只看Ta
狭义相对论中,时空空间是平直均匀的。也就是说只要两个观察者是相对静止的,他们看到的现象都一样。这东西在广义相对论里就不再成立了。爱因斯坦断言,两个相对静止的人看到的现象也可以是不一样的——甚至他们身上的手表也可以走得不一样快。要刻画这种现象,一般的空间概念已经不够了。一般空间当中,没有哪个点和别的点是不同的。它们的不同仅仅是坐标不同。除去坐标,各个点附近的性质都一样:在这个点附近的三角形内角和是180度,在那个点附近也是这样。装逼数学说法是:各点切空间上的度量是一致的。
然而,爱因斯坦描述的这种“不均匀性”是非常微小的。比如地球表面附近时空就不均匀是:每升高10m,时钟变快1.09×10^{-15}秒——这主要是因为每升高一些,地球引力场就减弱一些。于是钟表就走得快一些——怎样描述这种不均匀性就成了一个不小的难题。
后来,爱因斯坦学会了黎曼几何。他就用这个奇怪的数学工具来刻画这种时空的不均匀性。后代数学家和物理学家又很懒,就继承了他的这种描述方法——这当然不是唯一的描述方法,而且现在看来这个描述方法还有一些问题——这是引力场量子化困难的来源之一。
然而不论怎样,老爱的这种描述时空的方法(后来被称为广义相对论)被实验证明是成功的。它解释了很多牛顿理论解释不了的蛋疼问题(水星近日点进动等等)。其中最重要的应用之一就是GPS定位系统的相对论修正:
GPS的基本原理其实很简单,发若干个卫星到天上,每个卫星上装一个钟表(当然不是我家那种每天要上发条的摆钟),然后每个卫星都向地面发送一串信号告诉GPS接收机它上面钟表的时间。因为每个卫星的轨道参数是已知的,所以每个时刻每个卫星的位置也是已知的。然后根据你接受到的各个卫星发出来的信号,GPS接收机就可以计算(对比它受、收到的卫星上面的钟表的时间和自己的钟表时间的差)它和每个卫星的距离。然后简单的数学计算就知道自己的位置了。
然而这个过程实施起来那可真是蛋疼。首先你得把GPS接收机上的钟表和卫星上的钟表校对得高度同步。然后还得考虑卫星轨道的变化以及卫星发射和调姿过程带来的轨道参数误差。如果把这写“经典物理”带来的误差都扣除之后,你会发现GPS定位系统每天都会多出将近10km的定位误差。没错——这个误差就是相对论效应误差。
已经说了,卫星上的钟表比地面上的钟表海拔高得多,钟表应该走得快。然而卫星又高速运动,钟表应该走得慢。总之这些七七八八的相对论效应加在一起就不小了~
所以广义相对论离我门很近……
| 《大话物理——旅行到时与光的尽头》 第30节 作者: 一朵熊ss |
| 日期:2014-12-10 18:16:24 事件光锥 将时空方差还原到三维空间,其表达式如下: 物体由相对静止转换到匀速运动后,时间与空间在其身上的投影分别发生了延展与压缩,但作为整体而存在的时空方差却纹丝不变——不论作为观察者的第三方是跟随物体一同狂奔,还是静立一旁,他所测得的(ct)2与 l2差值永远为一常数。通过方差公式,我们还可以获取什么信息呢? 1907年,最初的惊诧过后,逐渐有学者悟出了狭义相对论中所蕴藏的变革力量。其中之一,便是曾因“恨铁不成钢”斥责过爱因斯坦的大数学家赫尔曼?闵可夫斯基(Hermann Minkowski),闵可夫斯基的父亲是俄国一犹太富商,由于沙俄间歇性的疯狂排犹,1872年,他带领家人搬迁到普鲁士的哥尼斯堡定居,此时的闵可夫斯基年方八岁,上面还有两位哥哥。不久,他欣喜地发现,隔壁邻居家住着一与他志趣相投的孩子:大卫?希尔伯特(David Hilbert),希尔伯特比他年长两岁,可是,一旦争论起数学题,他敏捷的才思、珠链炮似的发问常常让希尔伯特招架无力。备受打击的希尔伯特甚至开始怀疑自己的智商:“或许我根本就没那天分,隔壁家闵可夫斯基三兄弟才是做学问的料。”还好,这样的念头只是一闪而过,希尔伯特始终没舍得离弃他眷恋多年的数学,否则,“数学王国的亚历山大”就这样被折杀在了闵氏兄弟的光环之下……早慧的赫尔曼给大卫带来了巨大压力,但同时也是他动力的源泉,两人各自开拓了一片天地,多年后他们的人生的轨迹又在柯尼斯堡大学相交汇,此时,年龄总和还不到四十岁的两个年轻人皆已成为学界巨星,携手在数学与物理之间架起了座座桥梁。 读到爱因斯坦的论文时,闵可夫斯基已离开苏黎世追随希尔伯特的脚步入驻数学圣地哥廷根,他立马决定回头与当初那位并不太得意的门生展开合作,发挥自己所长,力图用形象化的几何语言为相对论时空注入新的活力。经过一年的摸索,闵可夫斯基第一个敏锐地意识到:若把“时空方差”带入真实情境,这个简单到不可思议的计算式可透露出发生于不同时间、不同地点的任意两个“事件”之间的秘密关系! 日期:2014-12-10 18:24:55 类时、类空与类光 举个例子:清晨8:00,住在翠湖之畔的你尽情享用过美味的甜甜圈&咖啡组合之后,神清气爽地跨出家门;下午16:00,高原之巅的玉龙雪山上,一朵雪莲悄然绽放。“人生不相见,动如参与商”,这两个注定没有交集的事件之间有着怎样的联系呢?粗略计算一下,昆明距离玉龙雪山约300千米(此处必须取两点间的直线距离),下午16时与清晨8点相距8小时=28800秒。所以, 相比天文数字级的时间平方值,距离的平方在此显得微乎其微。这意味着,在打开房门的一瞬,若有一微粒以光速c与你擦肩而过向着玉龙雪山奔去,它恰能在 之后,见证雪莲盈然而立的风姿。在微粒的视界,你与雪莲花之间并无丝毫间隔,当你双脚跨出家门时微粒亲历现场,而当雪莲迎风绽放时,可爱的小粒子也曾吻过它的脸庞。时间为光速而停驻,寻常人眼中的28800秒,对微粒来说即是永恒。 而这两个事件正是闵可夫斯基定义的三大时空关系之“类时”关联的一个示例,你有没有想过,假若有一天,你化作一粒尘埃在接近光速的世界里翱翔,将看到怎样的风景呢? 如图即是几何化后的时空方差,首先,依旧把三维空间简化作一维直线,即向着两端无限拓展的x轴,而纵轴是只能单向延伸的时间t,两轴垂直相交于原点。宇宙中发生的所有事件——从天琴座织女星的诞生到地球上一只虫子不小心打了个喷嚏被鸟儿发现——都可以用两条轴线间的某个小黑点标注出来。 从原点分别向两边45°方向各作一条直线,位于直线上的所有点方差恰等于零,也就是说,在光速移动者眼中,线上任意两个事件之间既没有时间间隔,也没有空间阻隔——它们根本就是同一事件——闵可夫斯基把这样的区域定义为“类光”区域。举个例子,从地球某一信号发射站向环绕我们的同步卫星发射一束光,那么从光的角度看,“信号从地球发射”与“卫星接收到信号”这两个事件间并无前与后、因与果的差别。 注:之所以选择45°是因为若以“光秒”作为距离单位,方差式中的c即被约化为1,由此可固定直线的斜率 |


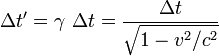


![t^*=\frac{c}{g} \cdot \ln \left[ \left(\sqrt{c^2 + v_0^2} - \frac{v_0}{\sqrt{1-\frac{v_0^2}{c^2}}} \right) \cdot \frac{\sqrt{c^2 + \left(g \cdot t + \frac{v_0}{\sqrt{1-\frac{v_0^2}{c^2}}}\right)^2} + g \cdot t + \frac{v_0}{\sqrt{1-\frac{v_0^2}{c^2}}}}{c^2} \right].](http://upload.wikimedia.org/math/1/8/6/18687aef85577e8c8df681cc8b0ea6c4.png)



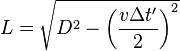




No comments:
Post a Comment