Sunday, March 8, 2015

group 1.满足封闭性：也就是这个处理所得到的元素，仍然被封闭在所定义的集合中——仍是属于所定义的集合的元素。[a+b=c (a,b,c∈整数集）用系统科学的语言来说，就是不产生“涌现”“突现”]。

1.满足封闭性：也就是这个处理所得到的元素，仍然被封闭在所定义的集合中——仍是属于所定义的集合的元素。[a+b=c  (a,b,c∈整数集）用系统科学的语言来说，就是不产生“涌现”“突现”]。


学习微分流形——理解李群流形
已有 2093 次阅读 2012-2-4 11:22 |个人分类:电脑围棋|系统分类:科研笔记|关键词:李群流形
要理解李群流形，先理解“群”。
“群”一直总是一个我没有花精力建立牢固理解的观念。这次顺便解决这个问题。
要定义一个“群”，
首先要定义一个集合，一个符号标志的集合（如整数集合）。这个集合的元素就是每个符号，可以认为是某一个基本状态或某类基本行为的标志。
然后，在这个集合的基础上再定义一种“处理”（如加法+），这种处理，使用集合中任意两个元素，得到另一个元素。
如果这样定义的集合和处理可以满足如下四条规则，则称这个集合和处理是一个“群”。
1.满足封闭性：也就是这个处理所得到的元素，仍然被封闭在所定义的集合中——仍是属于所定义的集合的元素。[a+b=c  (a,b,c∈整数集）用系统科学的语言来说，就是不产生“涌现”“突现”]。
2.满足结合律：也就是在用连续两次的处理来按顺序处理三个元素的时候，把前次对前2个元素的处理的结果与第三个元素再进行处理得到最后的结果，会和将第一个元素与“提前处理的后两个元素处理的结果”进行再次处理的结果相同。（a+b）+c = a+(b+c)
3.集合中存在有一个“0元素”。0元素使得对它和任意其他一个元素进行处理的时候，都会得到其他的那个元素，也就是，用它来处理，不会给其他的元素带来任何的变换。（如: 0 + x = x)
4.集合中任何的元素都有反元素。反元素使得将正元素和反元素进行处理的时候，无论先后次序如何，得到的结果都会是0元素。[如a+(-a)=0,(-a)+a=0].
 
群，可以应用理解为是对自然界中的“变化”用“集合”和“处理”来表达的模型，有2种基本的应用理解：
1.变化发生在“各种不同的状态”之间，变化靠“处理”来驱动。“各种不同的状态”的集合便是一个“状态空间”，处理是联系状态空间中不同状态的跃迁。只是，群，只规定了最基本的2元单类型处理跃迁（其他多元多类型处理的状态跃迁，总可以简化为两元单类型处理的复合结构）。从这个意义上来说，群，实际上就是一个“2元单处理的状态机”。
2.驱动变化的“各种处理”通过复合可以相互转化。这时是将“各种不同的处理”当集合，把将任意两个处理进行复合作为群的处理操作，得到的“驱动变化的处理”仍然是“各种不同的处理”中的一种。这表达了自然界的变化看上去总是循环往复的在驱动操作上的原因的一种假设。
 
接下来理解“李群”
以前导致我不能专心理解李群的原因之一，可能是我有一个大学的同学的姓名叫“李群”。我看到这两个字的大脑第一反应总是一个人的姓名，而不是一个数学上的“群”概念的一个特例。
摘一段百科上的说明如下：
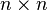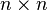李群主条目：李群 (数学) 李群(为纪念索菲斯·李而命名)是具有流形结构的群，就是说它们是局部上看起来像某个适当维度的欧几里得空间的空间。[69] 这里，作为额外结构的流形结构也必须是兼容的，就是说对应于乘法和求逆的映射必须是光滑的。标准例子是上面介绍的一般线性群: 它是所有 n .times n 矩阵的空间的开子集，因为它由不等式：det (A) ≠ 0，
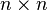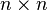给出。这里的 A 指示 n .times n 矩阵。[70]
李群在物理中是基础性的: 诺特定理把连续对称与守恒定律关联起来。[71] 在空间和时间中旋转和平移不变性是力学定律的基本对称。它们可以被用来构造简单的模型——比如在一种状况下实施轴对称常常会导致在解用来提供物理描述的方程上的重大简化。v[›] 另一个例子是洛伦兹变换，它有关于两个相互运动的观察者的时间和速度的测量。它们可以用纯群论方式推演，通过把变换表达为闵可夫斯基时空的旋转对称。在忽略万有引力的情况下，后者充当了狭义相对论的时空模型。[72] 闵可夫斯基时空的完全对称群，就是说包括了平移，叫做庞加莱群。通过上述联系，它在狭义相对论中扮演了关键角色，并隐含地用于量子场论。[73] 随位置变化的对称与规范场论一起构成现代物理对相互作用的描述的中心。[74]
待续...



李群 和 李代数

李群 是什么呢？李群 是 拥有 特定群结构 的 流形。我们这一篇就来看 李群 和 李代数。本节总体示意图见最下方。

Step1 李群定义

李群G是 有下列性质群运算 且 具有 群结构 的 流形
a.乘法 (,*,) : G \times G \rightarrow G, (g_1, g_2) \rightarrow g_1*g_2
b.逆运算 ()^{-1}: G\rightarrow G ,g \rightarrow g^{-1}
感觉有些抽象？学过群论的话就会感觉易如反掌。
举一些Nakahara文中例子 详细参见 Geometry Topology and Physics 2nd Edition ：
1.实数R 关于 定义在 R上的 加法 构成 Lie群（根据定义检查一下 a.”*”运算 这里就是一般的实数加法 b.逆运算()^{-1}就是实数减法   使用默认坐标函数其可微分性自明 c.单位元是0）
2.S^1 = {e^{i\theta} | \theta \in R (mod 2\pi)}亦即U(1)是Lie群
3.剩下的参见书上

对于 李群G的所有元素h定义  左移动L_g: G \rightarrow G,h \rightarrow L_gh = gh
很容易发现：L_a L_b h= L_a bh = L abh = L_{ab} h也就是 L_aL_b = L_{ab}符合所谓 群同态 条件

Step2 生成元

相信很多人知道QFT和GRT里，洛伦兹变换有所谓的生成元（Generator）为什么叫生成元呢？答案在这里。
拿出李群G的单位元e，根据 左移动 的定义，我们可以用 单位元生成所有的群元素！怎么做？L_ge = ge = g \forall g \in G就可以了。记得Lie群是流形，所以我们可以定义 单位元e上的 切平面 (T_eG)。哈哈，想起来之前说推进映射时  诱致 两个字了么？正是，我们来用 流形上 群元素之间的左移动 操作来 诱致   所有群元素切空间和单位群元素切空间之间  的操作，称之为L_{g*} : x \in T_eG\rightarrow T_gG, x \rightarrow L_{g*}x 。
接下来，当g遍历所有G的元素的时候，自然形成一个 和集合 TG \equiv \cup_ {\forall g \in G }\{ L_{g*}x | \forall x \in T_eG\},仔细看看是每一点这不就是Tangent Bundle（切从）么。因此我们就可以定义 流形上的向量场V_x|_g:G \rightarrow TG，g \rightarrow V_x|_g = L_{g*} x。
简单观察一下，如果取G中的两个元素g,h 则 gh \in G 所以 V_x|_{hg} = L_{hg*} x。同时如果根据推进映射我们定的V_x有L_{h*} \cdot L_{g*} V_x|_e = L_{h*} V_x|_g = V_x(L_h g) = V_x(hg) \equiv V_x|_{hg} 这样的性质的话，我们可得出L_{hg*} = L_{h*} \cdot L_{g*}可以叫做 诱致切同态（这名词书里不一定有 因为叫着方便 原创）。通过这个  诱致切同态 我们可以像Step1中定义左移动 一样 定义V_x 是 左不变向量场（意思就是 在流形上点g \in G 处的V_x通过 诱致切同态 映射到了点gh \in G的相同V_x的值, 所以向量场没有变，并且是 群的左作用 ，同理 群的右作用 一样）
不难看出上面的无论是李群G和其TG空间，都可以由e \in G来生成，这也就是为什么我们在QFT中 洛伦兹变换考虑所谓  生成子 的原因–其实就是李群的单位元（成矩阵那个 就是单位元的一个实现 （有些书称为 Representation 表达））

Step3   左不变向量空间 和 李代数 

既然有了  群上每一点处的左不变向量场 我们自然要看看能不能形成 向量空间。怎么看呢？首先我们得抽象出一个向量空间（就是先找一个集合，再看看这个集合中元素通过之前的定义会不会有符合向量空间的特殊关系）亦即 流形上所有 左不变向量场的集合\mathcal {I}。然后从这个集合中 拿出两个元素U, V看看关于线性结合是否成立等等。
思路有了，我们来验证一下：
a.线性结合的封闭性（closed）对于U,V \in \mathcal {I} 我们有 aU + bV \in \mathcal {I} (\forall a,b \in R)
b.逆元，单位元 都是自明的
自然\mathcal {I}是一个向量场
下面我们来谈李代数。代数 其实就是  左不变向量空间 附加 一个 双线性乘积 的结构，这里正是 推回映射 和 推进映射 例子 ：Lie（李）微分 中最后的 李括号。但是我们在这里以防万一还是要验证一下为好。
很简单机械操作。首先注意 李括号 是一个向量场。之后，根据左不变向量场定义，检查(L_{h*}[U,V]_L )|_h是否等于[U, V]_L|_{hg}就好了。注意这里的|_g脚标极其重要，是在哪个地方的操作，这个一定不能混！糊涂了的人可以留言 
为此我们引入测试函数 f:h\in G \rightarrow R。
回想推回映射定义\phi^* g(Q) = g(\phi (Q)) 同时根据 推进映射 定义则有(L_{h*}([U,V]_L |_g )) |_h[f] (h) =(L_h^{*}) (L_{h*}([U,V]_L |_g )) |_h[f] ( e)
(别被吓到，(L_{h*}([U,V]_L |_g )) |_h[f] (h) 的意思是  元素g上的李括号[U,V]被 算符 L_{h*} 推进到元素h上，然后作用到测试函数f上)
= (L_h^{*}) ([U,V]_L |_g ) [f\cdot L_h](e)
=(L_h^{*})\{ U(V[f\cdot L_h](e) ) - V(U[f\cdot L_h ](e) ) \}
=(L_h^{*})\{ U(L_{h*}V[f](h) ) - V(L_{h*}U[f ]) (h) \}
根据左不变向量的定义，我们有
=(L_h^{*})\{ U(V(hg)[f](h)) - V(U(hg)[f ](h)) \}
= \{U(hg)(V(hg)[f](h)) - V(hg)(U(hg)[f ](h)) \}
=[U,V]_L|_{hg}[f](h)
所以(L_{h*}[U,V]_L )|_h= [U, V]_L|_{hg}。证明完毕。
lie1

Copyright © 2014. All rights reserved.
Posted 十月 30, 2014 by guo.yansong.ngy@gmail.com in category 拓扑学（Topology），流形（Manifold）, 数学-教程




Minimization of Molecular Potential Energy Function Using ...

www.researchgate.net/.../267203972_Minimization_of_Molecular_Potentia...
Jan 12, 2015 - These two problems currently dominate the field of computational ... The search for the global minimum of a potential energy function is very difficult since the number of local minima grows exponentially with molecule size.

  • Minimizing molecular potential energy function using ...

    www.researchgate.net/.../259681045_Minimizing_molecular_potential_ene...
    Publication » Minimizing molecular potential energy function using genetic ... function problem is very challenging, since the number of local minima grows ... Solving the multi-objective flowline manufacturing cell scheduling problem by hybrid ...

  • [PDF]minimization of molecular potential energy function using ...

    ijamm.bc.cityu.edu.hk/ijamm/outbox/Y2010V6N9P1C92776126.pdf
    by JC Bansal - ‎2010 - ‎Cited by 4 - ‎Related articles
    Keywords: Global Minimum, potential energy function, particle swarm optimization, ... the potential energy function is nonconvex and therefore has many local.
    • Posted by at

    No comments:

    Post a Comment

    Subscribe to: Post Comments (Atom)