cc.sjtu.edu.cn/G2S/Utility/download2.aspx?type=2...
轉為繁體網頁
轉為繁體網頁
显示解析 - 菁优网
www.jyeoo.com/.../7170c2f0-e558-411f-b48c-56998337...
轉為繁體網頁
平凸透镜的弯曲表面是个曲面,球面的半径叫做这个曲面的曲率半径,把一个平凸透镜压在一块平面玻璃上,让红光从上方射入,如图所示,则从上往下看凸透镜,
轉為繁體網頁
博文
[转载]关于曲率 主曲率 高斯曲率
||
曲率曲率说明
表示曲线弯曲程度的量.
平面曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。曲率越大,表示曲线的弯曲程度越大。
K=lim|Δα/Δs|,Δs趋向于0的时候,定义K就是曲率。
曲率的倒数就是曲率半径。
圆弧的曲率半径,就是以这段圆弧为一个圆的一部分时,所成的圆的半径。 曲率半径越大,圆弧越平缓,曲率半径越小,圆弧越陡。曲率半径的倒数就是曲率。曲率 k = (转过的角度/对应的弧长)。当 角度和弧长同时趋近于0时,就是关于任意形状的光滑曲线的曲率的标准定义。而对于圆,曲率不随位置变化。
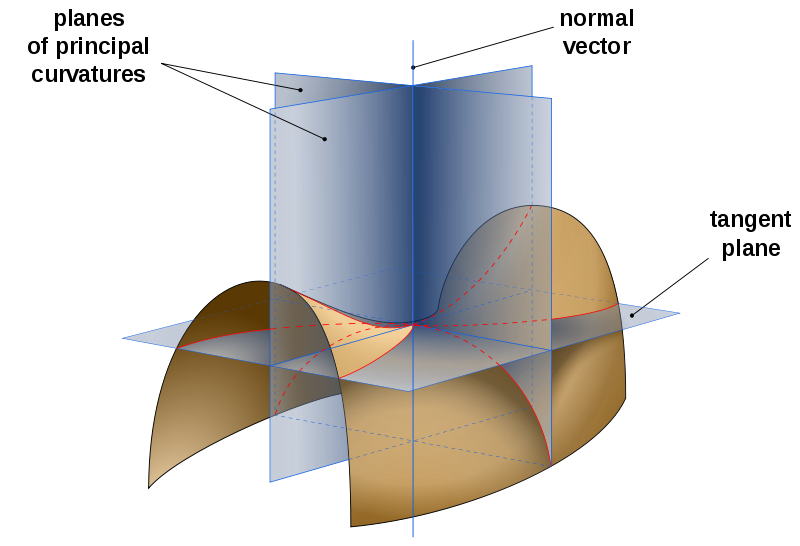
高斯曲率 曲面论中最重要的内蕴几何量。设曲 面在P点处 的两个主曲率为k1,k2,它们的乘积k=k1·k2称为曲面 于该点的总曲率或高斯曲率。它反映了曲面的一股弯曲程度。高斯曲率k的绝对值有明显的几何意义。设Δб是曲面上包含P点的一小片曲面(其面积仍用Δб表示),把Δб上的每点的单位法向量n平移到E3的原点O处,那么n的终点 的轨迹是 以O为中心的单位球面 S2上的一块区域 Δб* 。这个对应称为高斯映射。曲面在P点邻近弯曲程度可用Δб*( 其面积仍用Δб*表示)与Δб的面积比刻画。曲面在P点的 高斯曲率的 绝对值正是这个比值当Δб收缩成P点时的极限。
故事:
古典的几何学者在讨论三维空间中的曲面时,他们留意到曲面上每一点的曲率,都有两个不同的选择。比如在一个圆柱面上,一个方向是沿其横切的圆,另一个则是沿垂直线。
高斯在1827年发现这两个曲率的乘积具有惊人的属性。当我们令曲面在空间变型,只要它没有拉长缩短,这个积是不变的!后世称这个积为高斯曲率。
内蕴几何
高斯把这条定理写入《曲面通论》一书中。他指出必须把曲面的内在性质,即身处曲面内扁小甲虫所经验的属性,与其外在的,即依赖于曲面如何置于空间的性质区分开来,而只有内在性质,才值得“几何学家焚膏继晷,兀兀穷年地上下求索”。后世称研究这些性质的学问为内蕴几何。
高斯曲率决定曲面的内蕴几何
从球面剪取一片曲面,其高斯曲率为正常数。反过来说,局部而言,任何具正常曲率的曲面都可以等距地映射成球面的一部分。
类似地,从双曲曲面剪取的一片,其高斯曲率恒等于―1,而反过来说曲率等于―1的曲面与双面曲面局部相等。双曲曲面曾在讨论欧氏第五公理时论及。
高斯对几何的深思
高斯显然因他的定理兴奋不已。但他并没有认为人们对空间已认识透彻。
高斯:“我愈来愈相信,人类的理性并不能证明或理解几何的必要性。也许后世能对空间的本质有新的洞见,但目前这却是不可能的事。”
定义:
曲面论中最重要的内蕴几何量。设曲 面在P点处的两个主曲率为k1,k2,它们的乘积k=k1·k2称为曲面于该点的总曲率或高斯曲率。它反映了曲面的一股弯曲程度。高斯曲率k的绝对值有明显的几何意义。设Δб是曲面上包含P点的一小片曲面(其面积仍用Δб表示),把Δб上的每点的单位法向量n平移到E3的原点O处,那么n的终点的轨迹是以O为中心的单位球面 S2上的一块区域 Δб* 。这个对应称为高斯映射。曲面在P点邻近弯曲程度可用Δб*( 其面积仍用Δб*表示)与Δб的面积比刻画。曲面在P点的 高斯曲率的 绝对值正是这个比值当Δб收缩成P点时的极限。亦即
高斯曲率的符号则指明曲面弯曲的朝向。
http://blog.sciencenet.cn/blog-254499-739338.html 此文来自科学网刘金钊博客
上一篇:[转载]三维旋转矩阵实用算法(转)

曲率曲率说明
表示曲线弯曲程度的量.
平面曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。曲率越大,表示曲线的弯曲程度越大。
K=lim|Δα/Δs|,Δs趋向于0的时候,定义K就是曲率。
曲率的倒数就是曲率半径。
圆弧的曲率半径,就是以这段圆弧为一个圆的一部分时,所成的圆的半径。 曲率半径越大,圆弧越平缓,曲率半径越小,圆弧越陡。曲率半径的倒数就是曲率。曲率 k = (转过的角度/对应的弧长)。当 角度和弧长同时趋近于0时,就是关于任意形状的光滑曲线的曲率的标准定义。而对于圆,曲率不随位置变化。
高斯曲率 曲面论中最重要的内蕴几何量。设曲 面在P点处 的两个主曲率为k1,k2,它们的乘积k=k1·k2称为曲面 于该点的总曲率或高斯曲率。它反映了曲面的一股弯曲程度。高斯曲率k的绝对值有明显的几何意义。设Δб是曲面上包含P点的一小片曲面(其面积仍用Δб表示),把Δб上的每点的单位法向量n平移到E3的原点O处,那么n的终点 的轨迹是 以O为中心的单位球面 S2上的一块区域 Δб* 。这个对应称为高斯映射。曲面在P点邻近弯曲程度可用Δб*( 其面积仍用Δб*表示)与Δб的面积比刻画。曲面在P点的 高斯曲率的 绝对值正是这个比值当Δб收缩成P点时的极限。
故事:
古典的几何学者在讨论三维空间中的曲面时,他们留意到曲面上每一点的曲率,都有两个不同的选择。比如在一个圆柱面上,一个方向是沿其横切的圆,另一个则是沿垂直线。
高斯在1827年发现这两个曲率的乘积具有惊人的属性。当我们令曲面在空间变型,只要它没有拉长缩短,这个积是不变的!后世称这个积为高斯曲率。
内蕴几何
高斯把这条定理写入《曲面通论》一书中。他指出必须把曲面的内在性质,即身处曲面内扁小甲虫所经验的属性,与其外在的,即依赖于曲面如何置于空间的性质区分开来,而只有内在性质,才值得“几何学家焚膏继晷,兀兀穷年地上下求索”。后世称研究这些性质的学问为内蕴几何。
高斯曲率决定曲面的内蕴几何
从球面剪取一片曲面,其高斯曲率为正常数。反过来说,局部而言,任何具正常曲率的曲面都可以等距地映射成球面的一部分。
类似地,从双曲曲面剪取的一片,其高斯曲率恒等于―1,而反过来说曲率等于―1的曲面与双面曲面局部相等。双曲曲面曾在讨论欧氏第五公理时论及。
高斯对几何的深思
高斯显然因他的定理兴奋不已。但他并没有认为人们对空间已认识透彻。
高斯:“我愈来愈相信,人类的理性并不能证明或理解几何的必要性。也许后世能对空间的本质有新的洞见,但目前这却是不可能的事。”
定义:
曲面论中最重要的内蕴几何量。设曲 面在P点处的两个主曲率为k1,k2,它们的乘积k=k1·k2称为曲面于该点的总曲率或高斯曲率。它反映了曲面的一股弯曲程度。高斯曲率k的绝对值有明显的几何意义。设Δб是曲面上包含P点的一小片曲面(其面积仍用Δб表示),把Δб上的每点的单位法向量n平移到E3的原点O处,那么n的终点的轨迹是以O为中心的单位球面 S2上的一块区域 Δб* 。这个对应称为高斯映射。曲面在P点邻近弯曲程度可用Δб*( 其面积仍用Δб*表示)与Δб的面积比刻画。曲面在P点的 高斯曲率的 绝对值正是这个比值当Δб收缩成P点时的极限。亦即
高斯曲率的符号则指明曲面弯曲的朝向。
http://blog.sciencenet.cn/blog-254499-739338.html 此文来自科学网刘金钊博客
上一篇:[转载]三维旋转矩阵实用算法(转)
No comments:
Post a Comment