 成正比。就像爱因斯坦模型一样,它在高温时也与杜隆-珀蒂定律相符合。但由于模型的假设过于简化,它在中间的温度不太准确。
成正比。就像爱因斯坦模型一样,它在高温时也与杜隆-珀蒂定律相符合。但由于模型的假设过于简化,它在中间的温度不太准确。爱因斯坦模型[编辑]
维基百科,自由的百科全书
第一个假设是相当准确的,而第二个假设则不是。如果原子真的不互相作用,那么声波就不会在固体内传播。
历史上的影响[编辑]
原先的理论是由爱因斯坦在1907年提出的,具有很大的历史相关性。由杜隆-珀蒂定律所预言的固体的热容已经知道是与经典力学一致的。然而,低温下的实验观察表明,热容在绝对零度时趋于零,在高温时单调增加到杜隆-珀蒂定律的预言。利用普朗克的量子化假设,爱因斯坦第一次能够预言所观察到的实验趋势。与光电效应在一起,这成为需要量子化的最重要的证据之一(值得注意的是,爱因斯坦是在现代量子力学的出现的许多年之前解决了量子谐振子问题)。尽管它成功了,但是爱因斯坦却错误预言为指数趋近于零,而正确的表现则是遵守 幂定律。这个缺陷后来由德拜模型在1912年纠正。
幂定律。这个缺陷后来由德拜模型在1912年纠正。热容(微正则系综)[编辑]
恒定体积V的物体的热容,通过内能U定义为: 是系统的温度,可以从熵求出:
是系统的温度,可以从熵求出: 个原子所组成的固体,每一个原子都有3个自由度。因此,总共有
个原子所组成的固体,每一个原子都有3个自由度。因此,总共有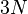 个量子谐振子(以下称SHO)。
个量子谐振子(以下称SHO)。 个能量量子分布在
个能量量子分布在 个SHO。我们可以想象把
个SHO。我们可以想象把 个石头分布在
个石头分布在 个盒子中:
个盒子中:或把一堆石头分成
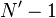 份:
份:或把
 个石头和
个石头和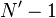 个划分排成一行:
个划分排成一行:最后一个图最能说明问题。把
 样东西排成一行,有
样东西排成一行,有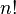 种方法。因此,把
种方法。因此,把 个石头和
个石头和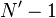 个划分排成一行的方法有
个划分排成一行的方法有 种,然而,如果把第2个划分和第5个划分互换位置,是没有任何不同的。相同的理由对量子也成立。为了得出可能的不可区分的排列方法,我们必须把排列的总数除以不可区分的排列的数目。一共有
种,然而,如果把第2个划分和第5个划分互换位置,是没有任何不同的。相同的理由对量子也成立。为了得出可能的不可区分的排列方法,我们必须把排列的总数除以不可区分的排列的数目。一共有 种相同的量子排列,以及
种相同的量子排列,以及 种相同的划分排列。因此,系统的多重性为:
种相同的划分排列。因此,系统的多重性为: 个能量量子放在
个能量量子放在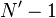 个谐振子中的方法数目。系统的熵具有下列形式:
个谐振子中的方法数目。系统的熵具有下列形式: 是一个很大的数,把它减去一总体上没有任何影响:
是一个很大的数,把它减去一总体上没有任何影响: :
:热容(正则系综)[编辑]
热容可以通过利用SHO的正则配分函数来获得。 以得出总量。接着,我们来计算每一个谐振子的平均能量:
以得出总量。接着,我们来计算每一个谐振子的平均能量: 给出:
给出:物理量
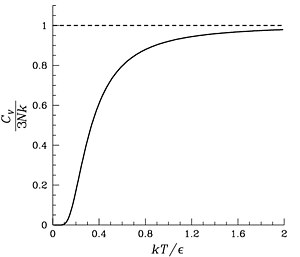
 的量纲是温度,是晶体的一个特有的性质。它称为“爱因斯坦温度”。因此,爱因斯坦晶体模型预言晶体的能量和热容是无量纲比率
的量纲是温度,是晶体的一个特有的性质。它称为“爱因斯坦温度”。因此,爱因斯坦晶体模型预言晶体的能量和热容是无量纲比率 的通用函数。类似地,德拜模型预言了比率
的通用函数。类似地,德拜模型预言了比率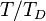 的通用函数。
的通用函数。









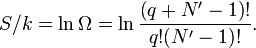
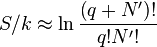


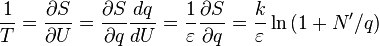











No comments:
Post a Comment