伊藤積分
維基百科,自由的百科全書
本條目需要精通或熟悉本主題的編者參與及協助編輯。(2011年12月13日) 請邀請適合的人士改善這篇條目。更多的細節與詳情請參見條目討論頁。您可以關注您所擅長領域的專家關注分類。
本條目沒有列出任何參考或來源。(2011年11月5日) 維基百科所有的內容都應該可供查證。 請協助添加來自可靠來源的引用以改善這篇條目。無法查證的內容可能被提出異議而移除。
伊藤微積分(英語:Itō calculus)得名自日本數學家伊藤清,是將微積分的概念擴展到隨機過程中,像布朗運動(維納過程)就可以用伊藤微積分進行分析。主要應用在金融數學及隨機微分方程中。伊藤微積分的中心概念是伊藤積分,是將傳統的黎曼-斯蒂爾傑斯積分延伸到隨機過程中,隨機過程一方面是一個隨機變數,而且也是一個不可微分的函數。
藉由伊藤積分,可以將一個隨機過程(被積分函數)對另一個隨機過程(積分變數)進行積分。積分變數一般會布朗運動。從 到
到 的積分結果是一個隨機變數。此隨機變數定義為一特定隨機變數序列的極限(有許多等效的方式可建構上述的定義)。
的積分結果是一個隨機變數。此隨機變數定義為一特定隨機變數序列的極限(有許多等效的方式可建構上述的定義)。
伊藤積分是對半鞅X以及隨機過程H的積分
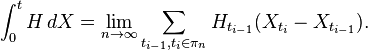
這裏X是布朗運動,或者更廣義地,是一個半鞅,H是一個適配於由X生成的篩選的,本地平方可積分的過程(Revuz & Yor 1999, Chapter IV)。布朗運動的路徑無法滿足應用於微積分標準技術的需求。特別地,其在任意點不可微,並且在每一個時間間隔都有無限方差。其結果是,無法用普通的方法定義積分(參考Riemann–Stieltjes integral)。主要的創新是只要調配被積函數,就可以定義一個積分,不嚴格的講,即t時刻它的值僅僅依靠此時刻之前的可用信息。 股票價格和其他可交易資產的價格可以通過隨機過程進行建模,例如布朗運動,或者,更經常的,幾何布朗運動(參見Black–Scholes)。然後,伊藤隨機積分代表,在時間t持有一定數量Ht的股票,對其進行連續交易的回報。這種情況下,調配H就相應於,在任何時候只使用可用信息的交易策略限制。這也阻止了通過高頻交易獲得無限收益的可能性:市場中每個上漲之前買入股票,每個下跌之前賣出股票。相似地,調配H的條件暗示,當作為黎曼和極限進行計算的時候,隨機積分不會收斂(Revuz & Yor 1999, Chapter IV)。 伊藤過程的重要結果包括,部分公式的集成和伊藤引理,即變量公式的變形。這些由於二次方差項,都與標準微積分公式不同,
本條目需要精通或熟悉本主題的編者參與及協助編輯。(2011年12月13日) 請邀請適合的人士改善這篇條目。更多的細節與詳情請參見條目討論頁。您可以關注您所擅長領域的專家關注分類。
本條目沒有列出任何參考或來源。(2011年11月5日) 維基百科所有的內容都應該可供查證。 請協助添加來自可靠來源的引用以改善這篇條目。無法查證的內容可能被提出異議而移除。
伊藤微積分(英語:Itō calculus)得名自日本數學家伊藤清,是將微積分的概念擴展到隨機過程中,像布朗運動(維納過程)就可以用伊藤微積分進行分析。主要應用在金融數學及隨機微分方程中。伊藤微積分的中心概念是伊藤積分,是將傳統的黎曼-斯蒂爾傑斯積分延伸到隨機過程中,隨機過程一方面是一個隨機變數,而且也是一個不可微分的函數。
藉由伊藤積分,可以將一個隨機過程(被積分函數)對另一個隨機過程(積分變數)進行積分。積分變數一般會布朗運動。從 到
到 的積分結果是一個隨機變數。此隨機變數定義為一特定隨機變數序列的極限(有許多等效的方式可建構上述的定義)。
的積分結果是一個隨機變數。此隨機變數定義為一特定隨機變數序列的極限(有許多等效的方式可建構上述的定義)。伊藤積分是對半鞅X以及隨機過程H的積分
伊藤积分[编辑]
维基百科,自由的百科全书
| 本条目需要精通或熟悉本主题的编者参与及协助编辑。(2011年12月13日) |
| 本条目没有列出任何参考或来源。(2011年11月5日) |
藉由伊藤积分,可以將一個隨機過程(被积分函数)對另一個隨機過程(積分變數)進行積分。積分變數一般會布朗运动。從
 到
到 的積分結果是一個隨機變數。此隨機變數定義為一特定隨機變數序列的極限(有許多等效的方式可建構上述的定義)。
的積分結果是一個隨機變數。此隨機變數定義為一特定隨機變數序列的極限(有許多等效的方式可建構上述的定義)。伊藤积分是对半鞅X以及随机过程H的积分
Semimartingale
From Wikipedia, the free encyclopedia
In probability theory, a real valued process X is called a semimartingale if it can be decomposed as the sum of a local martingale and an adapted finite-variation process. Semimartingales are "good integrators", forming the largest class of processes with respect to which the Itō integral and the Stratonovich integral can be defined.
The class of semimartingales is quite large (including, for example, all continuously differentiable processes, Brownian motion and Poisson processes). Submartingales and supermartingales together represent a subset of the semimartingales.
An Rn-valued process X = (X1,…,Xn) is a semimartingale if each of its components Xi is a semimartingale.
A real valued process X is a semimartingale if it is càdlàg, adapted, and for every t ≥ 0,
The class of semimartingales is quite large (including, for example, all continuously differentiable processes, Brownian motion and Poisson processes). Submartingales and supermartingales together represent a subset of the semimartingales.
Contents
[hide]Definition[edit]
A real valued process X defined on the filtered probability space (Ω,F,(Ft)t ≥ 0,P) is called a semimartingale if it can be decomposed asAn Rn-valued process X = (X1,…,Xn) is a semimartingale if each of its components Xi is a semimartingale.
Alternative definition[edit]
First, the simple predictable processes are defined to be linear combinations of processes of the form Ht = A1{t > T} for stopping times T and FT -measurable random variables A. The integral H · X for any such simple predictable process H and real valued process X isA real valued process X is a semimartingale if it is càdlàg, adapted, and for every t ≥ 0,



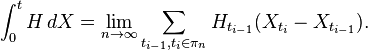



No comments:
Post a Comment