伊藤積分- Wikiwand
www.wikiwand.com/zh-hant/伊藤积分
其結果是，無法用普通的方法定義積分(參考Riemann–Stieltjes integral)。主要的創新是只要調配被積函數，就可以定義一個積分，不嚴格的講，即t時刻它的值僅僅依靠 ..."关键词=积分WIENER空间"_智立方 - 平台首页
lstc.ss.cqvip.com/.../articlesearch.aspx?...c%3A%5C%22积... - 轉為繁體網頁
24条记录 - 带导数的求积公式在一重积分Wiener空间下的平均误差 ... 在一定条件下构造函数的近似表示或者叫逼近，确定逼近的误差是函数逼近领域的基本问题，这些 ...Presentation "第九章Monte Carlo 积分. Monte Carlo 法的 ...
slideplayer.com/slide/7430189/
轉為繁體網頁
被积函数、积分边界复杂，难以用解析方法或一般的数值方法求解； 2. 被积函数的具体形式未知，只知道由模拟返回的函数值。 本章内容： 用Monte Carlo 法求定积分[PDF]Lebesgue积分的产生及其影响 - 浙江师范大学网络课程
course.zjnu.cn/hnc/shibian/Lebesgue.pdf
轉為繁體網頁
Riesz_Fisher 定理和20 世纪2030 Nobert Wiener Brown 运动理论历史的角度出发 ..... 是Dirichlet 积分和Riemann 积分g 刻画了Dirichlet 可积函数和Riemann 可积 ...音乐快递：phymath01 “ L2 是完备的” 意味着可以将L2 作为欧 ...
bbs.wenxuecity.com › 论坛 › 音乐快递
轉為繁體網頁
2011年11月16日 - Riesz-Fisher 定理和20 世纪20-30 Nobert Wiener Brown 运动理论. .... 的确, 他也证明了这一定理, 条件是积分区间有限而被积函数fn 一致有界.
信号处理的基本概念- 工欲善其事必先利其器- 博客频道 ...
blog.csdn.net/tianzhaixing/article/details/9118409
轉為繁體網頁
2013年6月18日 - 使用频率范围：指灵敏度随频率而变化的量值不超出给定误差的频率区间。 ... 抗混滤波：需要注意的是采样定理只保证了信号不被歪曲为低频信号，但不能保证不 ... 态过程；对周期信号，理论上采集一个周期信号就可以了，实际上，考虑信号平均的 .... 时域信号x(t)经过傅立叶积分变换可转换为频率函数x(t)或功率谱密度 ...
phymath999: 微積分五講第四講求Riemann 和時, Cauchy用 ...
phymath999.blogspot.com/2015/07/riemann-cauchy-riemann.html
2015年7月6日 - 別在於求Riemann 和時, Cauchy用的是小區間端點上的函數之值, 而Riemann 用的是小區間內 ... 時代的要求促成數學上一個空前活躍和富有創造性時期的誕生。 ..... Leibniz 假設可以求出一條曲線, 其縱坐標為z, 使得dz dx = y, 即 .... Newton 與Leibniz 的微積分的基礎是不牢固的, 是不嚴格的。 ..... (3) T. 16, 239-322.
伊藤积分[编辑]
维基百科，自由的百科全书
 | 本条目需要精通或熟悉本主题的编者参与及协助编辑。（2011年12月13日） |
 | 本条目没有列出任何参考或来源。（2011年11月5日） |
藉由伊藤积分，可以將一個隨機過程（被积分函数）對另一個隨機過程（積分變數）進行積分。積分變數一般會布朗运动。從
到
的積分結果是一個隨機變數。此隨機變數定義為一特定隨機變數序列的極限（有許多等效的方式可建構上述的定義）。伊藤积分是对半鞅X以及随机过程H的积分
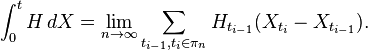
No comments:
Post a Comment