伊藤積分
維基百科，自由的百科全書
本條目需要精通或熟悉本主題的編者參與及協助編輯。（2011年12月13日） 請邀請適合的人士改善這篇條目。更多的細節與詳情請參見條目討論頁。您可以關注您所擅長領域的專家關注分類。
本條目沒有列出任何參考或來源。（2011年11月5日） 維基百科所有的內容都應該可供查證。 請協助添加來自可靠來源的引用以改善這篇條目。無法查證的內容可能被提出異議而移除。
伊藤微積分（英語：Itō calculus）得名自日本數學家伊藤清，是將微積分的概念擴展到隨機過程中，像布朗運動（維納過程）就可以用伊藤微積分進行分析。主要應用在金融數學及隨機微分方程中。伊藤微積分的中心概念是伊藤積分，是將傳統的黎曼－斯蒂爾傑斯積分延伸到隨機過程中，隨機過程一方面是一個隨機變數，而且也是一個不可微分的函數。
藉由伊藤積分，可以將一個隨機過程（被積分函數）對另一個隨機過程（積分變數）進行積分。積分變數一般會布朗運動。從
到
的積分結果是一個隨機變數。此隨機變數定義為一特定隨機變數序列的極限（有許多等效的方式可建構上述的定義）。伊藤積分是對半鞅X以及隨機過程H的積分
人大经济论坛
标题: 随机 分析 问题 [打印本页]作者: 行令于零 时间: 2011-8-22 21:21:37 标题: 随机 分析 问题
本帖最后由 wanghaidong918 于 2013-1-13 09:52 编辑
想问一下各位大牛 如果想要学习 随机分析 需要些什么数学基础 是不是只要 概率论和随机过程就够了 还要其他的么
此外i 请大家指教一下 如果想研究金融研究深一点 需要具备的数学有哪些 能简单说一下科目么 谢谢啊 谢谢
作者: xuruilong100 时间: 2011-8-22 23:04:43
泛函分析虽然基础，但重要，关键是它能改变你的思维方式，深化理解随机分析的体系建构。比如伊藤积分的定义，本质就是把积分看成一个线性算子，然后应用黎姿表示定理，找到对应的内积形式，将内积中的一个特定元素看做是随机积分
作者: 行令于零 时间: 2011-8-23 07:59:54
恩 谢谢了 出了泛函分析 还需要 测度 控制论等方面的系统学习么
作者: xuruilong100 时间: 2011-8-23 12:27:03
测度论是必须的，如果时间充裕可以专门学一学。时间不足的话，学一学高等概率论，高等概率论和测度论有重合的内容
作者: research 时间: 2011-8-23 14:17:58
楼主的问题简单啊！
你按某一名牌大学的
数学系概率统计专业的课程表学就是了！
作者: hadesli1987 时间: 2011-8-25 05:37:10
Risez 表示定理怎么应用到Ito formula 求指教....
作者: hadesli1987 时间: 2011-8-25 05:38:44
不会泛函的完全可以看懂 随机积分.... 测度勘一点点就够啦 主要培养你对于概率的直观认识 一个简单的题目比如问你 what is the expected time to have a head for a biased coin ?
作者: xuruilong100 时间: 2011-8-25 22:42:32
Ito公式中需要解决的最大的问题是“关于布朗运动的积分”或者“关于鞅的积分”，对于随机过程来说，直接套用LS积分的定义是不可行的（可以用布朗运动举出反例），所以，需要对“积分”作出新的定义。
关于“鞅”（布朗运动是最常用的鞅）的积分，本质是一个线性算子。如果可以将鞅构成的空间定义成为一个Hilbert空间，根据黎姿表示定理，关于x的线性算子Fx（y），y属于鞅空间，唯一对应一个内积形式（Ax，y），Ax和算子Fx（*）是对应的，那么Ax可以自然的规定为就是x构成的积分算子Fx（*）。
黄志远的《随机分析学基础》就是按上述逻辑结构讲解Ito积分的定义
作者: hadesli1987 时间: 2011-9-1 17:36:35
这样子啊 这么讲随机分析....只能说太坑爹了.... 既不是从Ito 的角度(Ito 是打算从切空间构造这个运动的轨迹，如同一个ODE一样) 也不是从金融的角度 给初学者讲这种东西 实在没有用处
作者: xuruilong100 时间: 2011-9-1 23:01:54
学点难的东西没坏处，打个比方，能喝高度酒的人不怕喝低度酒
作者: hadesli1987 时间: 2011-9-12 20:18:28
额 我比较倾向于美国的方法 把问题讲得直观 然后再进行 公立化
作者: linhaii 时间: 2011-9-22 17:03:42
看来很有难度
作者: baojie-911 时间: 2011-9-23 02:41:21
那么多的数学看起来好像都和金融相关，比如测度论、泛函分析等等，甚至关于伊藤积分也可以从比较高深的角度来理解，我以前就觉得应该把它们都学好了再来学金融。但是现在发现这样有点浪费时间，学了很多最后用的却是寥寥无几，金融里用来用去就那么点数学定理，搞清楚数学中的基本概念最重要，理解风险中性测度，理解鞅，理解伊藤积分的定义，这些就差不多了，其他的都是与它们相关的，真正需要的数学并不是那么多，重要的是理解它们的实质，金融毕竟不是数学。建议是先了解金融，想学数理金融，可以从金融的角度来理解数学，有了一个理解的对象要，学习那些太纯粹数学会简单很多，而且针对性也很强。
MIT牛人解说数学体系（推荐~） - 信息科学- 小木虫- 学术科研第一站
emuch.net/html/201405/7430848.html
轉為繁體網頁
2014年5月20日 - 13 篇文章 - 11 位作者
实分析（测度理论）：Lebesgue 不可测集的存在性泛函分析四个主要 ..... 随机积分（对随机过程的路径进行积分，其中比较有代表性的叫伊藤积分(Ito ...
Wiener泛函分数次正则性、连续性及伊藤公式推广.pdf-临时 ...
max.book118.com › 海量文档 › 临时分类 - 轉為繁體網頁
2014年10月25日 - 不幸的是，许多常见的泛函，例如伊藤积分或伊藤随机微分方程的解，相对于Wiener
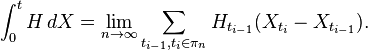
No comments:
Post a Comment