mingda1986: 回复 panzky : 但是通常不是解析的来做，而是dft，一方面画出能谱，一方面同时画出local的wave function，从而直接获得这些wave-function的overlap看出bonding的性质即可。 因为E(k)上没有空间的site的信息（如前述，是整块晶体的），所以为了考察局域的bonding，就回到了实空间。希望这样说清楚了
2013-10-13 04:02回复
mingda1986: 回复 panzky : 2个电子靠近形成了能级，进而整个晶体N个电子的spliting形成了能带。所以Bloch定义是N-周期性所导致的；然而看上去却像是单个电子的理论。整块固体的delocalized的电子就是简并电子，比如Fermi Liquid，所以：空间不同位置的delocalized电子，就是具有不同的晶格动量。
mingda1986: 回复 panzky : 只是空间不用能用于标记电子（直观的图像就是电子已经是de-Localized了）。这里区别core-level，exchange的Probability可以忽略，所以是distinguishable，而不是简并电子。这时，空间不同位置就把这些core electron分开成了不同的Hilbert Subspace.
描述
.gif)
Ic-通过超导体的临界电流，A
π - pi = 3.14
r-超导体的半径，m
Hc-零度时临界磁场强度，A/m
Tc-转变温度，K
T-超导体的温度，K
http://www.kepu.net.cn/gb/special/200911_01_trn/w3/01.html
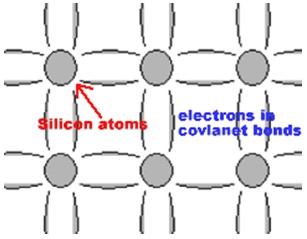当原子相互接近形成晶体时，不同原子的内外各电子壳层之间就有一定程度的交叠，相邻原子最外层交叠最多，内壳层交叠较少。原子组成晶体后，由于电子壳层的交叠，电子不再完全局限在某一原子上，可以由一个原子转移到相邻的原子上去，因而，电子可以在整个晶体中运动，这种运动称为电子的共有化运动。
电子只能在相似壳层间转移；最外层电子的共有化运动最显著；
当两个原子相距很远时，如同两个孤立的原子，每个能级是二度简并的。当两个原子互相靠近时，每个原子中的电子除了受到本身原子势场的作用，还要受到另一个原子势场的作用，其结果是每一个二度简并的能级都分裂为二个彼此相距很近的能级，两个原子靠得越近，分裂得越厉害。
当N个原子互相靠近形成晶体后，每一个N度简并的能级都分裂成N个彼此相距很近的能级，这N个能级组成一个能带，这时电子不再属于某一个原子而是在晶体中作共有化运动。分裂的每一个能带都称为允带，允带之间因没有能级称为禁带。
前面我们曾经介绍过，当N个原子相互靠近时，s能级便分裂成N个十分靠近的能级，形成能带，p能级是三度简并的，便分裂成3N个十分靠近的能级。由于N是个很大的数目，因而每个能带中的能级可以认为是连续的，有时称它们为“准连续的”。
但许多晶体的能带与孤立原子能级间的对应关系并非那样简单，因为一个能带不一定同孤立原子的某个能级相当，即不一定能区分s能级和p能级所过渡的能带
mingda1986: 回复 panzky :实空间的话x不是好量子数，这应该是从倒空间考虑的原因。这里倒不必是纠缠态，是N个电子delocalized占据整块固体的态就可以。每个晶格动量作为好量子数，已经是考虑了整块晶体的周期性，不是只是局域部位晶格动量不同——每个晶格动量的空间都是整个晶体。
去年的时候引用功能被楼中楼功能取代
BCS之美（四）：库伯对
mingda1986: 回复 panzky : 2个电子靠近形成了能级，进而整个晶体N个电子的spliting形成了能带。所以Bloch定义是N-周期性所导致的；然而看上去却像是单个电子的理论。整块固体的delocalized的电子就是简并电子，比如Fermi Liquid，所以：空间不同位置的delocalized电子，就是具有不同的晶格动量。
mingda1986: 回复 panzky : 只是空间不用能用于标记电子（直观的图像就是电子已经是de-Localized了）。这里区别core-level，exchange的Probability可以忽略，所以是distinguishable，而不是简并电子。这时，空间不同位置就把这些core electron分开成了不同的Hilbert Subspace.
描述
在超导体上通过电流，如果电流不是非常强，超导体仍然处于超导态，保持零电阻。增加电流值直至临界温度，使得超导体转到正常状态。这个值称为临界电流。当一个磁场被施加到超导体上市，临界电流降低。
将金属冷却转换成超导状态的临界温度以下，使载流电子组成库柏对。库柏对占据超导体的费米能级。超导体中能带隙将成对电子从在费米能级以上或者以下的未占据能级中分离出来。能带隙相当于拆开库柏对所需的能量。
当有电流通过超导体，成对电子执行平移然后获得一些动能。当通过超导体的电流值到达临界值时，这些能量超过了库柏对结合的能量，电子对分开，电阻不为零，超导体转为正常状态。
当有一个磁场施加到超导体时，场的强度从零增大到某一时间的最大值。不断变化的磁场引发超导体涡电场，使电子对旋转。电子对除了获得平动能之外，还有一些额外的转动能。旋转对可疑以一个较小值打破成对电子的平动能，因此可以获得一个较小的临界电流值。
因此，施加电场在超导体上可以减小通过超导体的临界电流值。
将金属冷却转换成超导状态的临界温度以下，使载流电子组成库柏对。库柏对占据超导体的费米能级。超导体中能带隙将成对电子从在费米能级以上或者以下的未占据能级中分离出来。能带隙相当于拆开库柏对所需的能量。
当有电流通过超导体，成对电子执行平移然后获得一些动能。当通过超导体的电流值到达临界值时，这些能量超过了库柏对结合的能量，电子对分开，电阻不为零，超导体转为正常状态。
当有一个磁场施加到超导体时，场的强度从零增大到某一时间的最大值。不断变化的磁场引发超导体涡电场，使电子对旋转。电子对除了获得平动能之外，还有一些额外的转动能。旋转对可疑以一个较小值打破成对电子的平动能，因此可以获得一个较小的临界电流值。
因此，施加电场在超导体上可以减小通过超导体的临界电流值。
应用条件
在宏观方面，电场中的电子旋转形成宏观电流变得明显。与楞次定律一直，这个电流产生了一个与外部磁场相反的内部磁场。在超导体内，外部磁场和内部磁场相互抵消。因此，在超导体内部，磁通量强度通常抵消为零。
优点
这个在超导体临界电流上的磁场效应可以被用来控制超导带材的一致性。
公式
Ic-通过超导体的临界电流，A
π - pi = 3.14
r-超导体的半径，m
Hc-零度时临界磁场强度，A/m
Tc-转变温度，K
T-超导体的温度，K
备注
1.转变温度是超导体转变成超导态的温度。 2.公式假定如下：
A）超导体的温度不低于转变温度的四分之三
B）超导体应该是圆柱形的形状，它的直径应该远小于长度
A）超导体的温度不低于转变温度的四分之三
B）超导体应该是圆柱形的形状，它的直径应该远小于长度
http://www.kepu.net.cn/gb/special/200911_01_trn/w3/01.html
半导体材料的基本结构
电子只能在相似壳层间转移；最外层电子的共有化运动最显著；
当两个原子相距很远时，如同两个孤立的原子，每个能级是二度简并的。当两个原子互相靠近时，每个原子中的电子除了受到本身原子势场的作用，还要受到另一个原子势场的作用，其结果是每一个二度简并的能级都分裂为二个彼此相距很近的能级，两个原子靠得越近，分裂得越厉害。
当N个原子互相靠近形成晶体后，每一个N度简并的能级都分裂成N个彼此相距很近的能级，这N个能级组成一个能带，这时电子不再属于某一个原子而是在晶体中作共有化运动。分裂的每一个能带都称为允带，允带之间因没有能级称为禁带。
前面我们曾经介绍过，当N个原子相互靠近时，s能级便分裂成N个十分靠近的能级，形成能带，p能级是三度简并的，便分裂成3N个十分靠近的能级。由于N是个很大的数目，因而每个能带中的能级可以认为是连续的，有时称它们为“准连续的”。
但许多晶体的能带与孤立原子能级间的对应关系并非那样简单，因为一个能带不一定同孤立原子的某个能级相当，即不一定能区分s能级和p能级所过渡的能带
mingda1986: 回复 panzky :实空间的话x不是好量子数，这应该是从倒空间考虑的原因。这里倒不必是纠缠态，是N个电子delocalized占据整块固体的态就可以。每个晶格动量作为好量子数，已经是考虑了整块晶体的周期性，不是只是局域部位晶格动量不同——每个晶格动量的空间都是整个晶体。
去年的时候引用功能被楼中楼功能取代
2013-6-17 08:18回复
mingda1986: 回复 砚鹊 : 看懂了当然是好事啊！ 那我考你两个问题吧，第一，如果说能带论意味着，N个电子都处于不同的态，岂不是说一块固体里的不同位置的电子的晶格动量必然不相同，这怎么理解？空间一处的电子怎么可能知道另外一处电子的动量呢？另外，从能带的角度，为什么会有绝缘体和导体之分？
2013-6-17 12:38回复
砚鹊: 回复 mingda1986 :第二问去知道里问了，没人鸟我
http://zhidao.baidu.com/question/560130970?quesup2&oldq=1
http://zhidao.baidu.com/question/560130970?quesup2&oldq=1
2013-6-18 17:40回复
mingda1986: 回复 panzky :实空间的话x不是好量子数，这应该是从倒空间考虑的原因。这里倒不必是纠缠态，是N个电子delocalized占据整块固体的态就可以。每个晶格动量作为好量子数，已经是考虑了整块晶体的周期性，不是只是局域部位晶格动量不同——每个晶格动量的空间都是整个晶体。
- mingda1986: 回复 panzky : 你说的E(k)的几何与解析性质，两个极端例子，一个是，水平线就表示localized state，没有dispersion,比如core-states,另一个极端比如Van Hove Singularity，态密度可以发散. bonding 和anti-bonding的话可以经验的判断，
2013-10-13 04:01回复 - mingda1986: 回复 panzky : 但是通常不是解析的来做，而是dft，一方面画出能谱，一方面同时画出local的wave function，从而直接获得这些wave-function的overlap看出bonding的性质即可。 因为E(k)上没有空间的site的信息（如前述，是整块晶体的），所以为了考察局域的bonding，就回到了实空间。希望这样说清楚了
2013-10-13 04:02回复 - mingda1986: 回复 panzky : 2个电子靠近形成了能级，进而整个晶体N个电子的spliting形成了能带。所以Bloch定义是N-周期性所导致的；然而看上去却像是单个电子的理论。整块固体的delocalized的电子就是简并电子，比如Fermi Liquid，所以：空间不同位置的delocalized电子，就是具有不同的晶格动量。
2013-10-21 11:47回复 - mingda1986: 回复 panzky : 只是空间不用能用于标记电子（直观的图像就是电子已经是de-Localized了）。这里区别core-level，exchange的Probability可以忽略，所以是distinguishable，而不是简并电子。这时，空间不同位置就把这些core electron分开成了不同的Hilbert Subspace.
2013-10-21 11:49回复 - mingda1986: 回复 panzky : 当然我完全知道我在说什么，同行也会知道。虽然我不觉得你是来讨论问题的，你好像只是背了一些名词然后完全没理解意思。最后一个我只是告诉你解析的判断DoS的走势很有问题，比如t2g这些晶格场效应，都是简化成能带的顶端的水平线。所以如果你需要真正计算，
2013-10-21 11:53回复 - mingda1986: 回复 panzky :DFT只是一个例子，你也可以用tight-binding，DoS与local能级的物理图像会更清楚. 当然，鉴于我发现自己花时间回复，收到的不是科学讨论而是你恶劣的态度，以及之前在私信的不礼貌行为，
2013-10-21 12:00回复 -
-
-
- mingda1986: 回复 panzky : DoS啊。。。我明白了你是想说用纵轴为E横轴为DoS的图吧。用能带是有原因的，除了把这两个联系起来，还有就是态密度就是diracdelta[w-E(k)]这个函数对于K空间的积分。。所以需要E(k)
BCS之美（四）：库伯对
|||
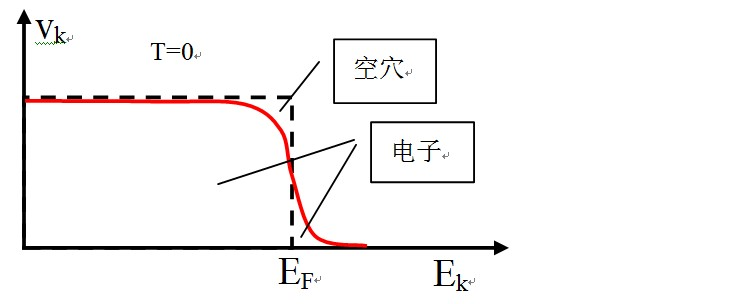
由于电子空穴组合，超导体内部电子在能量上的分布发生了变化。对于非超导材料来讲，温度为0的时候，电子填满在费米能级以下的所有能级。此时，如下图虚线所示，费米能级以上能级是空的，而费米能级以下是满的。但是，如果存在超导凝聚，在费米能级 EF附近，电子分布有一点点改变。此时，如下图红色实线所示，费米能级以上有了电子，费米能级以下有了空穴。
就是这样一个电子分布改变，导致超导体内电子发生凝聚。费米面附近的电子，也就是上图中红色曲线跨过EF附近的电子发生配对，形成动量为0的库伯对。由于它们的动量都是0，这就相当于玻色-爱因斯坦凝聚BEC。
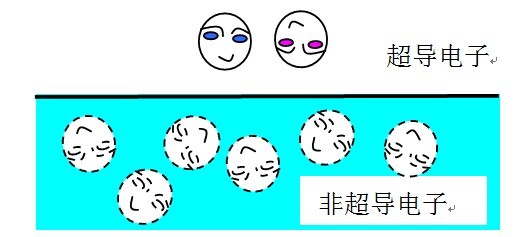
库伯对是很奇特的。一个库伯对中的两个电子并不像氢原子中的电子和质子结合在一起，而是像“潜水”一样，时而一起浮出“水面”时而一起潜入“水下”。一个库伯对可以写成 (uk+vkC†kC†−k)|0> 。其中 |vk|2 是两个电子浮出“水面”的概率，而|uk|2 是两个电子潜入“水面”的概率（这里的“水”指的是非超导电子）。越是靠近费米面，超导电子的潜入效果越显著。
如上图所示，库伯对中的两个电子，就像图中两哥们，在“水面”上下蹦来蹦去，而且他们步调一致。但在“水面”以下，它们就跟其他电子混在一起乱了。可见，这种配对的图像，跟很多人想象的配对是完全不同的。
超导凝聚的关键还在于，所有库伯对与共同的位相，也就是uk/vk 的位相相同。
（注：我写这个系列是个整理思路的过程。我发现，一边写还能一边有一些新想法。这是科普的好处。）
BCS之美（三）
BCS之美（一）
黄秀清错在哪里？
黄秀清错在哪里？
|||
这么多人给老黄推荐，编辑还给他加精，说明大家对老黄的“创新”抱着巨大的期望。可是，老黄的论文从08年开始写就，到今天也发不出去，难道都是评委错了？ 嗨，内行们就是不愿意给老黄指引一条明路，让他一个人在黑暗中乱撞，还自鸣得意要把BCS和量子力学一起干掉。他的精神固然可嘉可敬，但是，错误得太久会伤人的。
我觉得，老黄的错误集中在他对库伯对的理解上。早有人告诉他，库伯对是动量空间的，不是坐标空间的，可他偏就不信。他一定要把库伯对理解为舞台上一男一女跳舞。
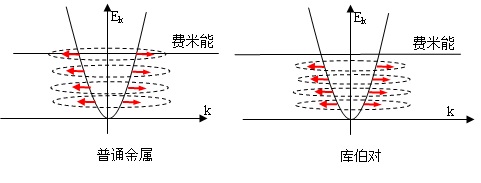
我给老黄画两个图，普通金属和超导在动量空间的能带图：
虽说是动量空间，可是一点也不奇怪，因为图中抛物线近似为自由电子的牛顿力学动能，它与动量的平方成正比。左边金属的费米能以下，电子占据了所有的正负动量（波矢k的\hbar倍)，有正方向的动量，也有反方向的动量。我用虚线把一对对动量相反的电子框起来。每一对红箭头，就表示两个动量相反的电子，你说它们是一对也好，不是一对也好，反正它们的动量相反，如此而已。这就像你此刻向右走，而西班牙一个女郎正好向左走，你们算不算一对你自己看着办。现在看右边超导里面的情况。情况跟金属几乎一样，只有一点点不同。一对正反动量的电子之间有一点点吸引力（势能为负），它们的总能量比在金属里面低了一点，所以，能量都向下移了一点。这样的状态在能量上更低，比左边金属的状态更稳定。这就是超导态。于是，费米面就空出来了，没电子了。费米面与最上面的电子对之间就有了间隙，叫能隙。这时每一对正负动量的电子就形成了库伯对（当然，还有些细节，比如一个库伯对是在配对和不配对之间晃动的）。可见，库伯对和金属里面的正负动量电子对其实是一一对应的。如果你还不能接受库伯对的配对，你就想想金属里面那一对正负动量的电子。它们也是一对，只不过两者之间没吸引。
但是，必须注意的是，任何一个k 都是大量电子的集体贡献，而不是一个电子。事实上任何一个电子都在跟别的电子和晶格频繁碰撞，它的动量瞬息万变。我们说一对动量相反的电子，其实是一个巨大的暗语。这一对电子并不是指坐标空间的两个真实的电子，而是大量电子的集体运动产生的粒子数为2的动量相反的电子组合。所以，动量空间的一对电子跟坐标空间一对电子一点关系也没有。特别是，根据测不准关系，动量确定的一对电子，坐标是完全不确定的。因而坐标空间的库伯对是一个很无聊的话题。
不知黄老是不是接受我这个解释。我担心他听明白了要跳楼，多年的心血化为灰烬。
后记：老黄还是不接受这个库伯对。我看他就是伤在这个“配”字上，要配就到实空间来配，他就看不惯电子偷偷摸摸在动量空间搞不正当关系，而他自己却没法进入这个动量空间，所以就分外眼红。呵呵呵，我看不如给库伯对改个名字，叫库伯dui如何? 不再说配对了，老黄没意见了吧？
No comments:
Post a Comment