This is Google's cache of http://spinningmass.gyrobattery.com/general-relativity/. It is a snapshot of the page as it appeared on Sep 3, 2015 17:19:54 GMT.
The current page could have changed in the meantime. Learn more
Full versionText-only versionView sourceTip: To quickly find your search term on this page, press Ctrl+F or ⌘-F (Mac) and use the find bar.
Spinning Mass
On Spinning Masses – The Wheel
General Relativity
From Wikipedia
General relativity, or the general theory of relativity, is the geometric theory of gravitation published by Albert Einstein in 1916[1] and the current description of gravitation in modern physics. General relativity generalises special relativity and Newton’s law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of partial differential equations.
Some predictions of general relativity differ significantly from those of classical physics, especially concerning the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light. Examples of such differences include gravitational time dilation, gravitational lensing, the gravitational redshift of light, and the gravitational time delay. The predictions of general relativity have been confirmed in all observations and experiments to date. Although general relativity is not the only relativistic theory of gravity, it is the simplest theory that is consistent with experimental data. However, unanswered questions remain, the most fundamental being how general relativity can be reconciled with the laws of quantum physics to produce a complete and self-consistent theory of quantum gravity.
Einstein’s theory has important astrophysical implications. For example, it implies the existence of black holes—regions of space in which space and time are distorted in such a way that nothing, not even light, can escape—as an end-state for massive stars. There is ample evidence that the intense radiation emitted by certain kinds of astronomical objects is due to black holes; for example, microquasars and active galactic nuclei result from the presence of stellar black holes and black holes of a much more massive type, respectively. The bending of light by gravity can lead to the phenomenon of gravitational lensing, in which multiple images of the same distant astronomical object are visible in the sky. General relativity also predicts the existence of gravitational waves, which since have been observed indirectly; a direct measurement is the aim of projects such as LIGO and NASA/ESA Laser Interferometer Space Antenna and various pulsar timing arrays. In addition, general relativity is the basis of current cosmological models of a consistently expanding universe.
Soon after publishing the special theory of relativity in 1905, Einstein started thinking about how to incorporate gravity into his new relativistic framework. In 1907, beginning with a simple thought experiment involving an observer in free fall, he embarked on what would be an eight-year search for a relativistic theory of gravity. After numerous detours and false starts, his work culminated in the presentation to the Prussian Academy of Science in November 1915 of what are now known as the Einstein field equations. These equations specify how the geometry of space and time is influenced by whatever matter and radiation are present, and form the core of Einstein’s general theory of relativity.[2]
The Einstein field equations are nonlinear and very difficult to solve. Einstein used approximation methods in working out initial predictions of the theory. But as early as 1916, the astrophysicist Karl Schwarzschild found the first non-trivial exact solution to the Einstein field equations, the so-called Schwarzschild metric. This solution laid the groundwork for the description of the final stages of gravitational collapse, and the objects known today as black holes. In the same year, the first steps towards generalizing Schwarzschild’s solution to electrically charged objects were taken, which eventually resulted in the Reissner–Nordström solution, now associated with electrically charged black holes.[3] In 1917, Einstein applied his theory to the universe as a whole, initiating the field of relativistic cosmology. In line with contemporary thinking, he assumed a static universe, adding a new parameter to his original field equations—the cosmological constant—to reproduce that “observation”.[4] By 1929, however, the work of Hubble and others had shown that our universe is expanding. This is readily described by the expanding cosmological solutions found by Friedmann in 1922, which do not require a cosmological constant. Lemaître used these solutions to formulate the earliest version of the Big Bang models, in which our universe has evolved from an extremely hot and dense earlier state.[5] Einstein later declared the cosmological constant the biggest blunder of his life.[6]
During that period, general relativity remained something of a curiosity among physical theories. It was clearly superior to Newtonian gravity, being consistent with special relativity and accounting for several effects unexplained by the Newtonian theory. Einstein himself had shown in 1915 how his theory explained the anomalous perihelion advance of the planet Mercury without any arbitrary parameters (“fudge factors“).[7] Similarly, a 1919 expedition led by Eddington confirmed general relativity’s prediction for the deflection of starlight by the Sun during the total solar eclipse of May 29, 1919,[8] making Einstein instantly famous.[9] Yet the theory entered the mainstream of theoretical physics and astrophysics only with the developments between approximately 1960 and 1975, now known as the golden age of general relativity.[10] Physicists began to understand the concept of a black hole, and to identify quasars as one of these objects’ astrophysical manifestations.[11] Ever more precise solar system tests confirmed the theory’s predictive power,[12] and relativistic cosmology, too, became amenable to direct observational tests.[13]

At the base of classical mechanics is the notion that a body‘s motion can be described as a combination of free (or inertial) motion, and deviations from this free motion. Such deviations are caused by external forces acting on a body in accordance with Newton’s second law of motion, which states that the net force acting on a body is equal to that body’s (inertial) mass multiplied by its acceleration.[15] The preferred inertial motions are related to the geometry of space and time: in the standard reference frames of classical mechanics, objects in free motion move along straight lines at constant speed. In modern parlance, their paths are geodesics, straight world lines in curved spacetime.[16]
Conversely, one might expect that inertial motions, once identified by observing the actual motions of bodies and making allowances for the external forces (such as electromagnetism or friction), can be used to define the geometry of space, as well as a time coordinate. However, there is an ambiguity once gravity comes into play. According to Newton’s law of gravity, and independently verified by experiments such as that of Eötvös and its successors (see Eötvös experiment), there is a universality of free fall (also known as the weak equivalence principle, or the universal equality of inertial and passive-gravitational mass): the trajectory of a test body in free fall depends only on its position and initial speed, but not on any of its material properties.[17] A simplified version of this is embodied in Einstein’s elevator experiment, illustrated in the figure on the right: for an observer in a small enclosed room, it is impossible to decide, by mapping the trajectory of bodies such as a dropped ball, whether the room is at rest in a gravitational field, or in free space aboard an accelerating rocket generating a force equal to gravity.[18]
Given the universality of free fall, there is no observable distinction between inertial motion and motion under the influence of the gravitational force. This suggests the definition of a new class of inertial motion, namely that of objects in free fall under the influence of gravity. This new class of preferred motions, too, defines a geometry of space and time—in mathematical terms, it is the geodesic motion associated with a specific connection which depends on the gradient of the gravitational potential. Space, in this construction, still has the ordinary Euclidean geometry. However, spacetime as a whole is more complicated. As can be shown using simple thought experiments following the free-fall trajectories of different test particles, the result of transporting spacetime vectors that can denote a particle’s velocity (time-like vectors) will vary with the particle’s trajectory; mathematically speaking, the Newtonian connection is not integrable. From this, one can deduce that spacetime is curved. The result is a geometric formulation of Newtonian gravity using only covariant concepts, i.e. a description which is valid in any desired coordinate system.[19] In this geometric description, tidal effects—the relative acceleration of bodies in free fall—are related to the derivative of the connection, showing how the modified geometry is caused by the presence of mass.[20]
With Lorentz symmetry, additional structures come into play. They are defined by the set of light cones (see the image on the left). The light-cones define a causal structure: for each event A, there is a set of events that can, in principle, either influence or be influenced by A via signals or interactions that do not need to travel faster than light (such as event B in the image), and a set of events for which such an influence is impossible (such as event C in the image). These sets are observer-independent.[23] In conjunction with the world-lines of freely falling particles, the light-cones can be used to reconstruct the space–time’s semi-Riemannian metric, at least up to a positive scalar factor. In mathematical terms, this defines a conformal structure.[24]
Special relativity is defined in the absence of gravity, so for practical applications, it is a suitable model whenever gravity can be neglected. Bringing gravity into play, and assuming the universality of free fall, an analogous reasoning as in the previous section applies: there are no global inertial frames. Instead there are approximate inertial frames moving alongside freely falling particles. Translated into the language of spacetime: the straight time-like lines that define a gravity-free inertial frame are deformed to lines that are curved relative to each other, suggesting that the inclusion of gravity necessitates a change in spacetime geometry.[25]
A priori, it is not clear whether the new local frames in free fall coincide with the reference frames in which the laws of special relativity hold—that theory is based on the propagation of light, and thus on electromagnetism, which could have a different set of preferred frames. But using different assumptions about the special-relativistic frames (such as their being earth-fixed, or in free fall), one can derive different predictions for the gravitational redshift, that is, the way in which the frequency of light shifts as the light propagates through a gravitational field (cf. below). The actual measurements show that free-falling frames are the ones in which light propagates as it does in special relativity.[26] The generalization of this statement, namely that the laws of special relativity hold to good approximation in freely falling (and non-rotating) reference frames, is known as the Einstein equivalence principle, a crucial guiding principle for generalizing special-relativistic physics to include gravity.[27]
The same experimental data shows that time as measured by clocks in a gravitational field—proper time, to give the technical term—does not follow the rules of special relativity. In the language of spacetime geometry, it is not measured by the Minkowski metric. As in the Newtonian case, this is suggestive of a more general geometry. At small scales, all reference frames that are in free fall are equivalent, and approximately Minkowskian. Consequently, we are now dealing with a curved generalization of Minkowski space. The metric tensor that defines the geometry—in particular, how lengths and angles are measured—is not the Minkowski metric of special relativity, it is a generalization known as a semi- or pseudo-Riemannian metric. Furthermore, each Riemannian metric is naturally associated with one particular kind of connection, the Levi-Civita connection, and this is, in fact, the connection that satisfies the equivalence principle and makes space locally Minkowskian (that is, in suitable locally inertial coordinates, the metric is Minkowskian, and its first partial derivatives and the connection coefficients vanish).[28]
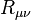 and the metric. Where
and the metric. Where  is symmetric. In particular,
is symmetric. In particular,
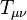 is the energy–momentum tensor. All tensors are written in abstract index notation.[30] Matching the theory’s prediction to observational results for planetary orbits (or, equivalently, assuring that the weak-gravity, low-speed limit is Newtonian mechanics), the proportionality constant can be fixed as κ = 8πG/c4, with G the gravitational constant and c the speed of light.[31] When there is no matter present, so that the energy–momentum tensor vanishes, the result are the vacuum Einstein equations,
is the energy–momentum tensor. All tensors are written in abstract index notation.[30] Matching the theory’s prediction to observational results for planetary orbits (or, equivalently, assuring that the weak-gravity, low-speed limit is Newtonian mechanics), the proportionality constant can be fixed as κ = 8πG/c4, with G the gravitational constant and c the speed of light.[31] When there is no matter present, so that the energy–momentum tensor vanishes, the result are the vacuum Einstein equations,
General relativity, or the general theory of relativity, is the geometric theory of gravitation published by Albert Einstein in 1916[1] and the current description of gravitation in modern physics. General relativity generalises special relativity and Newton’s law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of partial differential equations.
Some predictions of general relativity differ significantly from those of classical physics, especially concerning the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light. Examples of such differences include gravitational time dilation, gravitational lensing, the gravitational redshift of light, and the gravitational time delay. The predictions of general relativity have been confirmed in all observations and experiments to date. Although general relativity is not the only relativistic theory of gravity, it is the simplest theory that is consistent with experimental data. However, unanswered questions remain, the most fundamental being how general relativity can be reconciled with the laws of quantum physics to produce a complete and self-consistent theory of quantum gravity.
Einstein’s theory has important astrophysical implications. For example, it implies the existence of black holes—regions of space in which space and time are distorted in such a way that nothing, not even light, can escape—as an end-state for massive stars. There is ample evidence that the intense radiation emitted by certain kinds of astronomical objects is due to black holes; for example, microquasars and active galactic nuclei result from the presence of stellar black holes and black holes of a much more massive type, respectively. The bending of light by gravity can lead to the phenomenon of gravitational lensing, in which multiple images of the same distant astronomical object are visible in the sky. General relativity also predicts the existence of gravitational waves, which since have been observed indirectly; a direct measurement is the aim of projects such as LIGO and NASA/ESA Laser Interferometer Space Antenna and various pulsar timing arrays. In addition, general relativity is the basis of current cosmological models of a consistently expanding universe.
Soon after publishing the special theory of relativity in 1905, Einstein started thinking about how to incorporate gravity into his new relativistic framework. In 1907, beginning with a simple thought experiment involving an observer in free fall, he embarked on what would be an eight-year search for a relativistic theory of gravity. After numerous detours and false starts, his work culminated in the presentation to the Prussian Academy of Science in November 1915 of what are now known as the Einstein field equations. These equations specify how the geometry of space and time is influenced by whatever matter and radiation are present, and form the core of Einstein’s general theory of relativity.[2]
The Einstein field equations are nonlinear and very difficult to solve. Einstein used approximation methods in working out initial predictions of the theory. But as early as 1916, the astrophysicist Karl Schwarzschild found the first non-trivial exact solution to the Einstein field equations, the so-called Schwarzschild metric. This solution laid the groundwork for the description of the final stages of gravitational collapse, and the objects known today as black holes. In the same year, the first steps towards generalizing Schwarzschild’s solution to electrically charged objects were taken, which eventually resulted in the Reissner–Nordström solution, now associated with electrically charged black holes.[3] In 1917, Einstein applied his theory to the universe as a whole, initiating the field of relativistic cosmology. In line with contemporary thinking, he assumed a static universe, adding a new parameter to his original field equations—the cosmological constant—to reproduce that “observation”.[4] By 1929, however, the work of Hubble and others had shown that our universe is expanding. This is readily described by the expanding cosmological solutions found by Friedmann in 1922, which do not require a cosmological constant. Lemaître used these solutions to formulate the earliest version of the Big Bang models, in which our universe has evolved from an extremely hot and dense earlier state.[5] Einstein later declared the cosmological constant the biggest blunder of his life.[6]
During that period, general relativity remained something of a curiosity among physical theories. It was clearly superior to Newtonian gravity, being consistent with special relativity and accounting for several effects unexplained by the Newtonian theory. Einstein himself had shown in 1915 how his theory explained the anomalous perihelion advance of the planet Mercury without any arbitrary parameters (“fudge factors“).[7] Similarly, a 1919 expedition led by Eddington confirmed general relativity’s prediction for the deflection of starlight by the Sun during the total solar eclipse of May 29, 1919,[8] making Einstein instantly famous.[9] Yet the theory entered the mainstream of theoretical physics and astrophysics only with the developments between approximately 1960 and 1975, now known as the golden age of general relativity.[10] Physicists began to understand the concept of a black hole, and to identify quasars as one of these objects’ astrophysical manifestations.[11] Ever more precise solar system tests confirmed the theory’s predictive power,[12] and relativistic cosmology, too, became amenable to direct observational tests.[13]
From classical mechanics to general relativity
General relativity can be understood by examining its similarities with and departures from classical physics. The first step is the realization that classical mechanics and Newton’s law of gravity admit a geometric description. The combination of this description with the laws of special relativity results in a heuristic derivation of general relativity.Geometry of Newtonian gravity

According to general relativity, objects in a gravitational field behave similarly to objects within an accelerating enclosure. For example, an observer will see a ball fall the same way in a rocket (left) as it does on Earth (right), provided that the acceleration of the rocket provides the same relative force.
Conversely, one might expect that inertial motions, once identified by observing the actual motions of bodies and making allowances for the external forces (such as electromagnetism or friction), can be used to define the geometry of space, as well as a time coordinate. However, there is an ambiguity once gravity comes into play. According to Newton’s law of gravity, and independently verified by experiments such as that of Eötvös and its successors (see Eötvös experiment), there is a universality of free fall (also known as the weak equivalence principle, or the universal equality of inertial and passive-gravitational mass): the trajectory of a test body in free fall depends only on its position and initial speed, but not on any of its material properties.[17] A simplified version of this is embodied in Einstein’s elevator experiment, illustrated in the figure on the right: for an observer in a small enclosed room, it is impossible to decide, by mapping the trajectory of bodies such as a dropped ball, whether the room is at rest in a gravitational field, or in free space aboard an accelerating rocket generating a force equal to gravity.[18]
Given the universality of free fall, there is no observable distinction between inertial motion and motion under the influence of the gravitational force. This suggests the definition of a new class of inertial motion, namely that of objects in free fall under the influence of gravity. This new class of preferred motions, too, defines a geometry of space and time—in mathematical terms, it is the geodesic motion associated with a specific connection which depends on the gradient of the gravitational potential. Space, in this construction, still has the ordinary Euclidean geometry. However, spacetime as a whole is more complicated. As can be shown using simple thought experiments following the free-fall trajectories of different test particles, the result of transporting spacetime vectors that can denote a particle’s velocity (time-like vectors) will vary with the particle’s trajectory; mathematically speaking, the Newtonian connection is not integrable. From this, one can deduce that spacetime is curved. The result is a geometric formulation of Newtonian gravity using only covariant concepts, i.e. a description which is valid in any desired coordinate system.[19] In this geometric description, tidal effects—the relative acceleration of bodies in free fall—are related to the derivative of the connection, showing how the modified geometry is caused by the presence of mass.[20]
Relativistic generalization
As intriguing as geometric Newtonian gravity may be, its basis, classical mechanics, is merely a limiting case of (special) relativistic mechanics.[21] In the language of symmetry: where gravity can be neglected, physics is Lorentz invariant as in special relativity rather than Galilei invariant as in classical mechanics. (The defining symmetry of special relativity is the Poincaré group which also includes translations and rotations.) The differences between the two become significant when we are dealing with speeds approaching the speed of light, and with high-energy phenomena.[22]With Lorentz symmetry, additional structures come into play. They are defined by the set of light cones (see the image on the left). The light-cones define a causal structure: for each event A, there is a set of events that can, in principle, either influence or be influenced by A via signals or interactions that do not need to travel faster than light (such as event B in the image), and a set of events for which such an influence is impossible (such as event C in the image). These sets are observer-independent.[23] In conjunction with the world-lines of freely falling particles, the light-cones can be used to reconstruct the space–time’s semi-Riemannian metric, at least up to a positive scalar factor. In mathematical terms, this defines a conformal structure.[24]
Special relativity is defined in the absence of gravity, so for practical applications, it is a suitable model whenever gravity can be neglected. Bringing gravity into play, and assuming the universality of free fall, an analogous reasoning as in the previous section applies: there are no global inertial frames. Instead there are approximate inertial frames moving alongside freely falling particles. Translated into the language of spacetime: the straight time-like lines that define a gravity-free inertial frame are deformed to lines that are curved relative to each other, suggesting that the inclusion of gravity necessitates a change in spacetime geometry.[25]
A priori, it is not clear whether the new local frames in free fall coincide with the reference frames in which the laws of special relativity hold—that theory is based on the propagation of light, and thus on electromagnetism, which could have a different set of preferred frames. But using different assumptions about the special-relativistic frames (such as their being earth-fixed, or in free fall), one can derive different predictions for the gravitational redshift, that is, the way in which the frequency of light shifts as the light propagates through a gravitational field (cf. below). The actual measurements show that free-falling frames are the ones in which light propagates as it does in special relativity.[26] The generalization of this statement, namely that the laws of special relativity hold to good approximation in freely falling (and non-rotating) reference frames, is known as the Einstein equivalence principle, a crucial guiding principle for generalizing special-relativistic physics to include gravity.[27]
The same experimental data shows that time as measured by clocks in a gravitational field—proper time, to give the technical term—does not follow the rules of special relativity. In the language of spacetime geometry, it is not measured by the Minkowski metric. As in the Newtonian case, this is suggestive of a more general geometry. At small scales, all reference frames that are in free fall are equivalent, and approximately Minkowskian. Consequently, we are now dealing with a curved generalization of Minkowski space. The metric tensor that defines the geometry—in particular, how lengths and angles are measured—is not the Minkowski metric of special relativity, it is a generalization known as a semi- or pseudo-Riemannian metric. Furthermore, each Riemannian metric is naturally associated with one particular kind of connection, the Levi-Civita connection, and this is, in fact, the connection that satisfies the equivalence principle and makes space locally Minkowskian (that is, in suitable locally inertial coordinates, the metric is Minkowskian, and its first partial derivatives and the connection coefficients vanish).[28]
Einstein’s equations
Main articles: Einstein field equations and Mathematics of general relativity
Having formulated the relativistic, geometric version of the effects of gravity, the question of gravity’s source remains. In Newtonian gravity, the source is mass. In special relativity, mass turns out to be part of a more general quantity called the energy–momentum tensor, which includes both energy and momentum densities as well as stress (that is, pressure and shear).[29] Using the equivalence principle, this tensor is readily generalized to curved space-time. Drawing further upon the analogy with geometric Newtonian gravity, it is natural to assume that the field equation for gravity relates this tensor and the Ricci tensor, which describes a particular class of tidal effects: the change in volume for a small cloud of test particles that are initially at rest, and then fall freely. In special relativity, conservation of energy–momentum corresponds to the statement that the energy–momentum tensor is divergence-free. This formula, too, is readily generalized to curved spacetime by replacing partial derivatives with their curved-manifold counterparts, covariant derivatives studied in differential geometry. With this additional condition—the covariant divergence of the energy–momentum tensor, and hence of whatever is on the other side of the equation, is zero— the simplest set of equations are what are called Einstein’s (field) equations: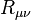 and the metric. Where
and the metric. Where  is symmetric. In particular,
is symmetric. In particular,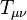 is the energy–momentum tensor. All tensors are written in abstract index notation.[30] Matching the theory’s prediction to observational results for planetary orbits (or, equivalently, assuring that the weak-gravity, low-speed limit is Newtonian mechanics), the proportionality constant can be fixed as κ = 8πG/c4, with G the gravitational constant and c the speed of light.[31] When there is no matter present, so that the energy–momentum tensor vanishes, the result are the vacuum Einstein equations,
is the energy–momentum tensor. All tensors are written in abstract index notation.[30] Matching the theory’s prediction to observational results for planetary orbits (or, equivalently, assuring that the weak-gravity, low-speed limit is Newtonian mechanics), the proportionality constant can be fixed as κ = 8πG/c4, with G the gravitational constant and c the speed of light.[31] When there is no matter present, so that the energy–momentum tensor vanishes, the result are the vacuum Einstein equations,
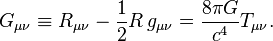


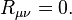
No comments:
Post a Comment