: 得到了數值樣本的平均值後再開根號
以振幅來說 平均應該是0(因為有方向性抵銷的關係), : 方均根看到的則是振幅波動的大小(但是看不到方向)
: 方均根看到的則是振幅波動的大小(但是看不到方向)
研究生教学用书：非电量电测技术（第3版） - 京东网上商城
item.jd.com/11482882.html
轉為繁體網頁
轉為繁體網頁
作者: pdo () 看板: ShuLin4-11
標題: [問題] 方均根和平均的差別？
時間: Fri Jun 10 12:39:25 2005
我有一筆振幅資料
我做方均根和平均
那方均根到底代表什麼意思？
而平均又代表什麼意思冽？
我在想 平均大概可以看出來是以哪個地方當成基準點上下振動
那方均根？？
先謝謝回答囉.....^^
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 140.115.66.229
> -------------------------------------------------------------------------- <
作者: crazyking (遇過才知道...) 看板: ShuLin4-11
標題: Re: [問題] 方均根和平均的差別？
時間: Fri Jun 10 15:11:30 2005
依我以前學統計的印象...
方均根的好處是
每一筆資料因為平方之後
不會像平均一樣會因資料可能含有負值而相戶底消資料的真實變動情況
一筆變動很大的資料 平均起來可能會是很靠近0(如果以0為基準點的資料來說)
方均根則會讓你了解 資料的確有變化性存在
※ 引述《pdo ()》之銘言：
: 我有一筆振幅資料
: 我做方均根和平均
: 那方均根到底代表什麼意思？
: 而平均又代表什麼意思冽？
: 我在想 平均大概可以看出來是以哪個地方當成基準點上下振動
: 那方均根？？
: 先謝謝回答囉.....^^
--
拂長劍 寄白雲
一生一愛一瓢飲
舞秋月 佾江風
也是疏狂也任真
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 218.166.114.119
※ 編輯: crazyking 來自: 218.166.114.119 (06/10 15:12)
> -------------------------------------------------------------------------- <
作者: janifer (小怪獸不怕冷) 看板: ShuLin4-11
標題: Re: [問題] 方均根和平均的差別？
時間: Fri Jun 10 19:48:15 2005
※ 引述《crazyking (遇過才知道...)》之銘言：
: 依我以前學統計的印象...
: 方均根的好處是
: 每一筆資料因為平方之後
: 不會像平均一樣會因資料可能含有負值而相戶底消資料的真實變動情況
: 一筆變動很大的資料 平均起來可能會是很靠近0(如果以0為基準點的資料來說)
: 方均根則會讓你了解 資料的確有變化性存在
: ※ 引述《pdo ()》之銘言：
: : 我有一筆振幅資料
: : 我做方均根和平均
: : 那方均根到底代表什麼意思？
: : 而平均又代表什麼意思冽？
: : 我在想 平均大概可以看出來是以哪個地方當成基準點上下振動
: : 那方均根？？
: : 先謝謝回答囉.....^^
印象中是熱力學裡面的吧...利用平均動能推導出分子方均根速率
(我上高中物理的時候好像沒學過 不過以前家教有教過XD)
跟上面講的類似 統計學裡面也有此類觀念
因為樣本與平均之間的差值是有方向性的
以振幅來說 平均應該是0(因為有方向性抵銷的關係)
方均根看到的則是振幅波動的大小(但是看不到方向)
手邊有普物或熱力的書的話 翻翻看可能比較正確
我只是憑印象......
--
我夢見草原
我夢見太陽花
還有你
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 218.169.68.87
※ 編輯: janifer 來自: 218.169.68.87 (06/10 20:03)
推 pdo:謝謝兩位的解答啦 ^^ 我懂了 140.115.66.229 06/10
> -------------------------------------------------------------------------- <
作者: max2 (終極的B-I三角形) 看板: ShuLin4-11
標題: Re: [問題] 方均根和平均的差別？
時間: Fri Jun 10 21:57:23 2005
※ 引述《janifer (小怪獸不怕冷)》之銘言：
: ※ 引述《crazyking (遇過才知道...)》之銘言：
: : 依我以前學統計的印象...
: : 方均根的好處是
: : 每一筆資料因為平方之後
: : 不會像平均一樣會因資料可能含有負值而相戶底消資料的真實變動情況
: : 一筆變動很大的資料 平均起來可能會是很靠近0(如果以0為基準點的資料來說)
: : 方均根則會讓你了解 資料的確有變化性存在
: 印象中是熱力學裡面的吧...利用平均動能推導出分子方均根速率
: (我上高中物理的時候好像沒學過 不過以前家教有教過XD)
: 跟上面講的類似 統計學裡面也有此類觀念
: 因為樣本與平均之間的差值是有方向性的
: 以振幅來說 平均應該是0(因為有方向性抵銷的關係)
: 方均根看到的則是振幅波動的大小(但是看不到方向)
: 手邊有普物或熱力的書的話 翻翻看可能比較正確
: 我只是憑印象......
肥頭依你的解答; 就有機會得到諾貝爾獎囉!
我只能理解10%...
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 218.166.97.36
推 janifer:............. 218.169.68.87 06/11
> -------------------------------------------------------------------------- <
作者: eaglez (苦命小員工) 看板: ShuLin4-11
標題: Re: [問題] 方均根和平均的差別？
時間: Sun Jun 12 19:56:58 2005
※ 引述《janifer (小怪獸不怕冷)》之銘言：
: ※ 引述《crazyking (遇過才知道...)》之銘言：
: : 依我以前學統計的印象...
: : 方均根的好處是
: : 每一筆資料因為平方之後
: : 不會像平均一樣會因資料可能含有負值而相戶底消資料的真實變動情況
: : 一筆變動很大的資料 平均起來可能會是很靠近0(如果以0為基準點的資料來說)
: : 方均根則會讓你了解 資料的確有變化性存在
: 印象中是熱力學裡面的吧...利用平均動能推導出分子方均根速率
: (我上高中物理的時候好像沒學過 不過以前家教有教過XD)
: 跟上面講的類似 統計學裡面也有此類觀念
: 因為樣本與平均之間的差值是有方向性的
: 以振幅來說 平均應該是0(因為有方向性抵銷的關係)
: 方均根看到的則是振幅波動的大小(但是看不到方向)
: 手邊有普物或熱力的書的話 翻翻看可能比較正確
: 我只是憑印象......
又到了鷹爺爺的變態時光了
今天我門要說的是芳軍根
所謂的芳 就是指美眉身上的味道
所謂的軍 就是指軍隊
所謂的根 就是指那玩意
所以芳軍根 就是指軍妓
謝謝大家 鷹爺爺的每日一變態時光就這樣結束啦 掰掰
好吧 認真鷹的歡樂時光繼續開始吧
所謂的方均根 就是rms值
就是把每個數值樣本 先平方一次再全部加總起來求平均值
得到了數值樣本的平均值後再開根號
就得到了沒有意義的rms值了
那麼就英飛凌的一顆powermos來看
好像叫做IRFB20N3C 他的耐電壓應該是600伏特 耐電流應該是20安培
詳細的規格我忘記了 不過還要考慮到有關頻率或者溫度跟一大堆什麼姬芭鳥的
突波電流或者突波電壓 就不管了
那 20 安培應該指的就是rms值
想知道其他的就等馬把她表妹獻上來再說
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 218.32.104.174
> -------------------------------------------------------------------------- <
作者: max2 (終極的B-I三角形) 看板: ShuLin4-11
標題: Re: [問題] 方均根和平均的差別？
時間: Sun Jun 12 22:18:53 2005
※ 引述《eaglez (苦命小員工)》之銘言：
: ※ 引述《janifer (小怪獸不怕冷)》之銘言：
: 又到了鷹爺爺的變態時光了
: 今天我門要說的是芳軍根
: 所謂的芳 就是指美眉身上的味道
: 所謂的軍 就是指軍隊
: 所謂的根 就是指那玩意
: 所以芳軍根 就是指軍妓
: 謝謝大家 鷹爺爺的每日一變態時光就這樣結束啦 掰掰
: 好吧 認真鷹的歡樂時光繼續開始吧
: 所謂的方均根 就是rms值
: 就是把每個數值樣本 先平方一次再全部加總起來求平均值
: 得到了數值樣本的平均值後再開根號
: 就得到了沒有意義的rms值了
: 那麼就英飛凌的一顆powermos來看
: 好像叫做IRFB20N3C 他的耐電壓應該是600伏特 耐電流應該是20安培
: 詳細的規格我忘記了 不過還要考慮到有關頻率或者溫度跟一大堆什麼姬芭鳥的
: 突波電流或者突波電壓 就不管了
: 那 20 安培應該指的就是rms值
: 想知道其他的就等馬把她表妹獻上來再說
老鷹莖，光憑你的這句話；你就可以入選諾貝爾文學獎了。
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 218.166.119.172
高中物理教材內容討論:氣體方均根速率式子的意義
www.phy.ntnu.edu.tw/demolab/phpBB/viewtopic.php?topic=22652
2009年12月19日 - 13 篇文章
在氣體動力論中 為了氣體壓力等效的關係所以這裡的速率是方均根速率. P=Nmv2/
2006年4月21日
2006年3月21日
2006年3月12日
2004年11月27日
何謂方均根速率？ - Yahoo!奇摩知識+
https://tw.knowledge.yahoo.com/question/question?qid=1105041401761
何謂均方根(RMS) - Yahoo!奇摩知識+
https://tw.knowledge.yahoo.com/question/question?qid=1305091616053
方均根速率的具体实际物理意义是什么？_百度知道
方均根速率_百度百科
baike.baidu.com/view/2478568.htm
轉為繁體網頁
轉為繁體網頁
速率的均方根(一) - 加百列的部落格- udn部落格
blog.udn.com/Gabriel33/3839052
[問題] 方均根和平均的差別？ - 精華區- 批踢踢實業坊
https://www.ptt.cc/man/ShuLin4-11/DF2/.../M.1140417292.A.5C8.html
精華區- 批踢踢實業坊
https://www.ptt.cc/man/Chemistry/D706/.../M.1177812733.A.AB0.html
Root-Mean-Square Speed - Kinetic Molecular Theory - Boundless
https://www.boundless.com/chemistry/gases/.../root-mean-square-speed
已翻譯： 根均方速度- 分子運動論- 大千世界
Learn more about root-mean-square speed in the Boundless open textbook. The root-mean-square speed is a measure of the speed of particles in a gas, ...均方根速度- 维基百科，自由的百科全书
zh.wikipedia.org/zh-hk/均方根速度
轉為繁體網頁
轉為繁體網頁
[PDF]
http://quantivity.wordpress.com/2011/02/21/why-log-returns/
human mathematics permalink
August 23, 2011 11:48 am
Regarding the paper links: There is no perfect objective metric. Log returns assumes that investors hate variance per se, whereas in fact investors hate drawdowns. Investors also hate some integral of drawdowns convolved with a convex function of time. Unless they subscribe to some philosophy, e.g. buy-and-hold-and-never-let-go, that has taught them otherwise.[DOC]
误差理论与数据处理 - 湖北省教育考试院
www.hbea.edu.cn/files/.../06018误差理论与数据处理.doc
轉為繁體網頁
轉為繁體網頁
每個數值樣本 先平方一次再全部加總起來求平均值
: 得到了數值樣本的平均值後再開根號
以振幅來說 平均應該是0(因為有方向性抵銷的關係), : 方均根看到的則是振幅波動的大小(但是看不到方向)
: 方均根看到的則是振幅波動的大小(但是看不到方向)
0Comment count
|
1View count
|
8/10/14
| |||||
0Comment count
|
1View count
|
8/10/14
| |||||
逢甲大學統計與精算研究所碩士論文 - 逢甲大學學位論文提交 ...
ethesys.lib.fcu.edu.tw/ETD-search/getfile?URN=etd-0222110...etd...
μ (對數常態模型) ....................... 177. 表8-4-13 不同殘差下之預測標準誤的變化率(
Logarithmic growth
From Wikipedia, the free encyclopedia
A familiar example of logarithmic growth is the number of digits needed to represent a number, N, in positional notation, which grows as logb (N), where b is the base of the number system used, e.g. 10 for decimal arithmetic.[3] In more advanced mathematics, the partial sums of the harmonic series
Logarithmic growth can lead to apparent paradoxes, as in the martingale roulette system, where the potential winnings before bankruptcy grow as the logarithm of the gambler's bankroll.[5] It also plays a role in the St. Petersburg paradox.[6]
In microbiology, the rapidly growing exponential growth phase of a cell culture is sometimes called logarithmic growth. During this bacterial growth phase, the number of new cells appearing are proportional to the population. This terminological confusion between logarithmic growth and exponential growth may possibly be explained by the fact that exponential growth curves may be straightened by plotting them using a logarithmic scale for the growth axis.[7]
Uncommon Returns through Quantitative and Algorithmic Trading
Why Log Returns
February 21, 2011
A reader recently asked an important question, one which often puzzles those new to quantitative finance (especially those coming from technical analysis, which relies upon price pattern analysis):
Begin by defining a return: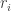
at time 
, where 
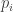is the price at time and 
:
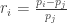
Benefit of using returns, versus prices, is normalization: measuring all variables in a comparable metric, thus enabling evaluation of analytic relationships amongst two or more variables despite originating from price series of unequal values. This is a requirement for many multidimensional statistical analysis and machine learning techniques. For example, interpreting an equity covariance matrix is made sane when the variables are both measured in percentage.
Several benefits of using log returns, both theoretic and algorithmic.
First, log-normality: if we assume that prices are distributed log normally (which, in practice, may or may not be true for any given price series), then
is conveniently normally distributed, because:
This is handy given much of classic statistics presumes normality.
Second, approximate raw-log equality: when returns are very small (common for trades with short holding durations), the following approximation ensures they are close in value to raw returns:
, 
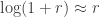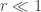
Third, time-additivity: consider an ordered sequence of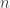
trades. A statistic frequently calculated from this sequence is the compounding return, which is the running return of this sequence of trades over time:
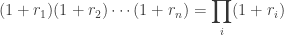
This formula is fairly unpleasant, as probability theory reminds us the product of normally-distributed variables is not normal. Instead, the sum of normally-distributed variables is normal (important technicality: only when all variables are uncorrelated), which is useful when we recall the following logarithmic identity:
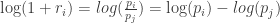
Thus, compounding returns are normally distributed. Finally, this identity leads us to a pleasant algorithmic benefit; a simple formula for calculating compound returns:
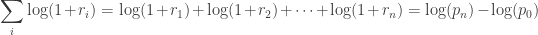
Thus, the compound return over n periods is merely the difference in log between initial and final periods. In terms of algorithmic complexity, this simplification reduces O(n) multiplications to O(1) additions. This is a huge win for moderate to large n. Further, this sum is useful for cases in which returns diverge from normal, as the central limit theorem reminds us that the sample average of this sum will converge to normality (presuming finite first and second moments).
Fourth, mathematical ease: from calculus, we are reminded (ignoring the constant of integration):
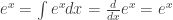
This identity is tremendously useful, as much of financial mathematics is built upon continuous time stochastic processes which rely heavily upon integration and differentiation.
Fifth, numerical stability: addition of small numbers is numerically safe, while multiplying small numbers is not as it is subject to arithmetic underflow. For many interesting problems, this is a serious potential problem. To solve this, either the algorithm must be modified to be numerically robust or it can be transformed into a numerically safe summation via logs.
As suggested by John Hall, there are downsides to using log returns. Here are two recent papers to consider (along with their references):
Why use the logarithm of returns, rather than price or raw returns?The answer is several fold, each of whose individual importance varies by problem domain.
Begin by defining a return:
at time , where is the price at time and :Benefit of using returns, versus prices, is normalization: measuring all variables in a comparable metric, thus enabling evaluation of analytic relationships amongst two or more variables despite originating from price series of unequal values. This is a requirement for many multidimensional statistical analysis and machine learning techniques. For example, interpreting an equity covariance matrix is made sane when the variables are both measured in percentage.
Several benefits of using log returns, both theoretic and algorithmic.
First, log-normality: if we assume that prices are distributed log normally (which, in practice, may or may not be true for any given price series), then
is conveniently normally distributed, because:This is handy given much of classic statistics presumes normality.
Second, approximate raw-log equality: when returns are very small (common for trades with short holding durations), the following approximation ensures they are close in value to raw returns:
, Third, time-additivity: consider an ordered sequence of
trades. A statistic frequently calculated from this sequence is the compounding return, which is the running return of this sequence of trades over time:This formula is fairly unpleasant, as probability theory reminds us the product of normally-distributed variables is not normal. Instead, the sum of normally-distributed variables is normal (important technicality: only when all variables are uncorrelated), which is useful when we recall the following logarithmic identity:
Thus, compounding returns are normally distributed. Finally, this identity leads us to a pleasant algorithmic benefit; a simple formula for calculating compound returns:
Thus, the compound return over n periods is merely the difference in log between initial and final periods. In terms of algorithmic complexity, this simplification reduces O(n) multiplications to O(1) additions. This is a huge win for moderate to large n. Further, this sum is useful for cases in which returns diverge from normal, as the central limit theorem reminds us that the sample average of this sum will converge to normality (presuming finite first and second moments).
Fourth, mathematical ease: from calculus, we are reminded (ignoring the constant of integration):
This identity is tremendously useful, as much of financial mathematics is built upon continuous time stochastic processes which rely heavily upon integration and differentiation.
Fifth, numerical stability: addition of small numbers is numerically safe, while multiplying small numbers is not as it is subject to arithmetic underflow. For many interesting problems, this is a serious potential problem. To solve this, either the algorithm must be modified to be numerically robust or it can be transformed into a numerically safe summation via logs.
As suggested by John Hall, there are downsides to using log returns. Here are two recent papers to consider (along with their references):
- Comparing Security Returns is Harder than You Think: Problems with Logarithmic Returns, by Hudson (2010)
- Quant Nugget 2: Linear vs. Compounded Returns – Common Pitfalls in Portfolio Management, by Meucci (2010)
30 Comments leave one →
Trackbacks
- Finanzas 101: Calculos con Retornos « Quantitative Finance Club
- Why Minimize Negative Log Likelihood? « Quantivity
- Why log returns? « mathbabe
- Geometric Efficient Frontier « Systematic Investor
- Pathetic Model Using VIX To Predict S&P 500, Part 1 | Curated Alpha
- Links 30 Mar « Pink Iguana
- franziss | Pearltrees
- Pair Trading Model « ickyatcity
- Learning Algorithmic Trading | Bordering Insanity
- Misleading Elvish Statistics | Chen's blog
- Why log returns ? |
- Why Use Log Returns? | Châteaux de Bah
均方根速度- 维基百科，自由的百科全书
zh.wikipedia.org/zh-hk/均方根速度
轉為繁體網頁
[PDF]
方均根速率：. 2 v v v. = 氣體分子的方均根速率以符號. 表示，定義成 rms rms. 方均根
氣體動力論氣體動力論
www.cyut.edu.tw/~jjliaw/pages/96_01_course/physics/.../9630061.pdf
大部分氣體粒子的速率ump、平均速率uavg與方均根速率urms ...
blog.udn.com/Gabriel33/4170587
速率的均方根(一) - 加百列的部落格- udn部落格
blog.udn.com/Gabriel33/3839052
精華區- 批踢踢實業坊
https://www.ptt.cc/man/Chemistry/D706/.../M.1177812733.A.AB0.html
何謂均方根(RMS) - Yahoo!奇摩知識+
https://tw.knowledge.yahoo.com/question/question?qid=1305091616053
高中物理教材內容討論:氣體方均根速率式子的意義
www.phy.ntnu.edu.tw/demolab/phpBB/viewtopic.php?topic=22652
2009年12月19日 - 13 篇文章
在氣體動力論中 為了氣體壓力等效的關係所以這裡的速率是方均根速率. P=Nmv2/
2006年3月21日
2004年11月13日
2004年2月24日
百度知道搜索_均方根速度
z.baidu.com/search?word=均方根速度&lm=0...
轉為繁體網頁
root-mean-square speed - 均方根速率 - 學術名詞暨辭書資訊網
terms.naer.edu.tw/detail/1329985/
[PPT]
分子速率小于最概然速率、平均速率和方均根速率的分子数占分子总数的比例为多少？ 利用Γ函数可简化计算。 Γ函数的定义为. 当n为整数时，通过分部积分可直接 ...
8_5平均速率和方均根速率.ppt
kczx.hnu.cn/G2S/.../20120423111548_942245635521.pp...
轉為繁體網頁
In my own study, I was convinced most by the explanation in Meucci’s Risk and Asset Allocation book. There are hints of what he says in what you say. Basically, his argument is that you should take some invariants and then map them to expected market prices. Since you should be concerned about how these invariants move forward into time and how they can be combined into market prices, the properties of the invariants are more important than the properties of the final market prices (arithmetic returns are easy to aggregate for 1 point in time, but geometric returns are better to aggregate through time). Also, as you note, there is an easy formula to convert one to the other.
I was a bit tripped up in his analysis b/c if the geometric returns follow some garch or regime-switching process, then they aren’t IID. However, the log returns of these variables can still be projected in each period following these processes and then mapped to market prices for use in optimization. Meucci has a good short paper on why you shouldn’t use the projection of log returns in optimization on ssrn.
It might be even more complicated than downsides — maybe brief upsides vs spiky upsides vs long-and-steady affects how investors take the downside. I’m reading The Big Short right now. It’s incredible how Michael Burry’s investors lampooned him, even when he was RIGHT, calling the biggest short of the last decade with surgical precision. http://books.google.com/books?id=eParwQ0YdrcC&printsec=frontcover&dq=the+big+short&hl=en&src=bmrr&ei=vQ9VTpCDN8K_tgfDl_CPAg&sa=X&oi=book_result&ct=book-thumbnail&resnum=1&ved=0CEIQ6wEwAA#v=onepage&q=his%20investors&f=false
Sure – you have my email now – so beep at me when you’ve finished it.
‘X’ amount of profit is a quantity in a 10-digit space,which gives a distorted view of natural quantities. One has to take the natural logarithm of a naturally occured quantity to bring it down to the undistorted /real scale. This is why it is called ‘Natural’ Logarithm. Hence, we takke the natural logiartihm of the returns to apply summation and substraction operations on them.
This is also why , the ln() of the returns has a normal distribution..This is also why, linear interpolation works on the ln() of the returns.
Why dont you write $\log(r_n) – \log(r_0)$ instead?
want. There need to be more things like this on WordPress
Have a related question and maybe you can provide guidance.
You said:
“… if we assume that prices are distributed log normally (which, in practice, may or may not be true for any given price series)”
“… given much of classic statistics presumes normality”
Question: How material is the “normality assumption” in creating profitable quant models and strategies?
How can one discern when this assumption is realistic (worth working with as a practitioner) and when is it purely for academical reasons?
Allow me to elaborate based on my limited knowledge so far.
It seems that the vast majority of quantitative education is founded on the normality assumption and on the creation of models from historical distributions.
“Risk” seems to be about going (or not going) outside the first/second standard deviation of the Gaussian curve.
As a trader, it almost sounds like this was born in a “buy and hold” world where time works in an investor`s favor.
Also as a trader, I know that outside the first standard deviations is where the best trades are in this volatile world.
On the other hand (from the Gaussian assumption), quant practitioners like Nassim Taleb advocate for non Gaussian ways.
Some highlights below:
“Granted, it has been tinkered with, using such methods as complementary “jumps”, stress testing, regime switching or the elaborate methods known as GARCH, but while they represent a good effort, they fail to address the bell curve’s fundamental flaws.
…
These two models correspond to two mutually exclusive types of randomness: mild or Gaussian on the one hand, and wild, fractal or “scalable power laws” on the other. Measurements that exhibit mild randomness are suitable for treatment by the bell curve or Gaussian models, whereas those that are susceptible to wild randomness can only be expressed accurately using a fractal scale. The good news, especially for practitioners, is that the fractal model is both intuitively and computationally simpler than the Gaussian, which makes us wonder why it was not implemented before.
…
Indeed, this fractal approach can prove to be an extremely robust method to identify a portfolio’s vulnerability to severe risks. Traditional “stress testing” is usually done by selecting an arbitrary number of “worst-case scenarios” from past data. It assumes that whenever one has seen in the past a large move of, say, 10 per cent, one can conclude that a fluctuation of this magnitude would be the worst one can expect for the future. This method forgets that crashes happen without antecedents. Before the crash of 1987, stress testing would not have allowed for a 22 per cent move.
…
Any attempts to refine the tools of modern portfolio theory by relaxing the bell curve assumptions, or by “fudging” and adding the occasional “jumps” will not be sufficient. We live in a world primarily driven by random jumps, and tools designed for random walks address the wrong problem. It would be like tinkering with models of gases in an attempt to characterise them as solids and call them “a good approximation”.
Pasted from the “A focus on the exceptions that prove the rule” article on ft dot com.
Like I said at the beginning I am looking for a quant edge and need a way to navigate through the vast knowledge and avoid assumptions that are incompatible with a practitioner`s reality.
Can you please offer some criteria and/or references that would help me navigate?
Is the Gaussian assumption safe as foundation for profitable models?
How to verify this?
In practice, the single most important concept to understand is the existence and distinction between alpha model and risk model; and use of the correct corresponding quantitative methodology for each.
- Alpha model: describes how you make money; use whatever model makes the best money
- Risk model: describes your downside risk exposure; use whatever model best describes reality of the alpha phenomenon
Many folks unknowingly conflate the two. Avoid that.To your specific questions:
Q: How material is the “normality assumption” in creating profitable quant models and strategies?
A: Irrelevant for alpha model; if a model makes money (whatever the distribution), trade it. Maybe relevant for risk model, if alpha phenomenon is best described by a non-Gaussian distribution.
Q: How can one discern when this assumption is realistic (worth working with as a practitioner) and when is it purely for academical reasons?
A: Build and then measure: build a risk model, trade over time, and then measure whether you lose more money than you expect. If you are losing more than your model says, then one of your assumptions is wrong.
Q: Vast majority of quantitative education is founded on the normality assumption and on the creation of models from historical distributions.
A: Historical accident. Gaussian distributions (and exponential distributions, more generally) are mathematically convenient, so much of closed-form Q world is built on them. Modern computational finance and ML methods, such as Monte Carlo methods (e.g. particle filters), are mostly agnostic to distribution assumptions.
Q: Is the Gaussian assumption safe as foundation for profitable models?
A: Maybe or maybe not. Models should be built to describe reality. Blind adherence to any unverified mathematical assumption(s) are likely to lead to hardship in trading.
Q: How to verify this?
A: Many diverse statistical techniques exist. QQ-plot is an elementary technique from exploratory analysis which may be applicable.
Q: Can you please offer some criteria and/or references that would help me navigate?
A: Strive to build models that describe reality. Use the best tools at your disposal and make as few unverified assumptions as possible. Continuously check reality to verify it matches your assumptions.