[PDF]
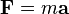 仍然成立,但质量也会变得随参考系的不同而不同。以上原因导致加速度在牛顿力学中那种因为简洁而具有的优越性,在狭义相对论中不复存在,必須使用更有功能的數學工具,即張量分析
仍然成立,但质量也会变得随参考系的不同而不同。以上原因导致加速度在牛顿力学中那种因为简洁而具有的优越性,在狭义相对论中不复存在,必須使用更有功能的數學工具,即張量分析從量綱看世界 - 中研院數學研究所
w3.math.sinica.edu.tw/math_media/d333/33302.pdf
基本量(單位)
一個完整的單位至少需要三個基本單位(unit)。回顧中學學過的物理課, 一般的物理有
cgs 制或MKS 制, 以cgs 制而言; c 是公分(cm)、g 是公克(g)、s 是秒(second)。因此
長度(L), 質量(M), 時間(T)
就是一個物理系統的基本單位, 基本單位不能以其它的物理量定義之, 其它的物理量都可以化
為這三個量之冪次方的乘積稱之為導出量(induced unit)。
數學傳播33卷3期, pp. 13-27
從量綱看世界
林琦焜
1. 前言
『當對你討論之事物能加以測量並且能以數字表示時, 則你對它已有所了解, 但當你
不能以數字表示時, 你的知識是含糊且不充分; 這或許是知識的開始, 但無論如何你
的思想尚未進入科學的領域。』
— William Thomson (Lord Kelvin), 1824–1907 —
量綱(因次) 分析(dimensional analysis) 很難說從何時、何地、何人正式開始, 因
此很難為它立碑建傳, 基本上它是想推廣古希臘幾何中的相似與比例的觀念。所有的大師如牛
頓、Maxwell、Boltzmann、Lord Kelvin、Planck、Einstein.... 等等, 他們在處理問題時內心深
處其實是有量綱(dimension) 的概念, 但基本上是case by case ! 法國數學家J. Fourier
(1768–1830) 的名著: 熱的解析理論(Analytical Theory of Heat) 就出現量綱分析的論述,
20世紀初量綱分析才逐漸成形, 並且是物理學、數學中建立數學模型的重要方法之一。量綱分
析是一門非常值得研究和學習的知識, 它是探討科學規律, 解決科學和工程問題的一個有效的
工具。概念是這樣:
當一個理論被表述為一組方程式時, 倘若理論與現實有所聯繫的話, 那麼抽象的符號
必須與現實的物理特徵連結。
通過量綱分析可以檢查反映物理現象規律的方程在計量方面是否合理。它是在經驗和實驗的基
礎上, 利用物理定律的量綱平衡(齊次) 原則, 確定各物理量之間的關係。一個成熟的物理學家
如果要探究某一個問題的時候, 往往是從定性或者半定量的角度入手分析, 他所使用的方法就
是像數量級、量綱分析、對稱性分析等等。二次世界大戰期間英國流體力學大師G. I. Taylor
(3/7/1886-6/27/1975)為著研究原子彈爆炸, 從量綱分析的角度引進新的變數(similar variables)
將Euler 方程化為常微分方程, 從而得出自相似解(self-similar solution), 這結果甚
至比美國國防部的機密資料還精確, 害得美國國防部官員要調查是否有洩密事件。
13
14 數學傳播33卷3期民98年9月
我個人於1988年至1992年在美國的University of Arizona (Tucson, Arizona) 修讀
博士學位, 該校以應用數學見長, 尤其是流體力學、孤立子(Soliton) 理論還有動態系統(Dynamical
System) 等更是有特色, 因此有機會接觸這方面的大師級人物, 其中印象最深刻的是
V. Zakharov 的課(Nonlinear Wave), 他是俄國人, 因此聽他的英文實在是萬分痛苦(非常
重的喉音), 聽起來像是北極熊, 但他確實是大人物, 只見黑板上任意的方程式這項比一比, 那項
比一比, 解的形式就出來了, 似乎是在變魔術, 對我而言是極大的震撼, 但我確信這個方法絕對
不難。還好Zakharov 教授寫了非常簡潔的講義, 每天只好拿著這份講義(至今我仍然保存著)
對著它發呆(參禪), 一天、兩天, 一星期、兩星期, 一個月、兩個月, 就在某一天騎腳踏車回宿
舍的路上, 突然之間頓悟了(Eureka!)。回到宿舍之後也顧不得晚餐, 所謂打鐵趁熱或套句宗教
術語不要消滅聖靈的感動(學數學絕對不能讓心中那份感動消失!),將以前學過的東西一一逐項
檢驗是否合理, 一直到天亮, 從那時起我就成為量綱分析的忠實信徒。在此也給讀者一個良心的
建議: 多散步或騎腳踏車, 放慢人生的步伐才有可能成為數學家(哲學家)。
2. 量綱之概念
『我們有可能在不依賴於任何特殊個體或物質的條件下, 給出長度、質量、時間和溫
度的單位, 並使其意義不隨時間而變, 不因文化而異; 即使外星文明和超人社會也是
如此, 永遠如此。』
— Max Planck (1858–1947) —
2.1. 基本量(單位)
一個完整的單位至少需要三個基本單位(unit)。回顧中學學過的物理課, 一般的物理有
cgs 制或MKS 制, 以cgs 制而言; c 是公分(cm)、g 是公克(g)、s 是秒(second)。因此
長度(L), 質量(M), 時間(T)
就是一個物理系統的基本單位, 基本單位不能以其它的物理量定義之, 其它的物理量都可以化
為這三個量之冪次方的乘積稱之為導出量(induced unit)。我們也可以改為長度、速度、質量,
但一般而言是取長度、質量、時間為基本單位。藉由量綱分析處理問題時這三個量會不斷出現,
也請讀者記得它們代表基本單位。
2.2. 導出量
由基本量做排列組合就是導出量。按牛頓的思想:
『數字不單純是一個數字, 而是具有物理本質的量。』
從量綱看世界15
要了解一個物理量,最好的方式就是明白其量綱(dimension), 量綱本質上就是單位(unit), 例
如速度(velocity)、加速度(acceleration)
v =
dx
dt
=⇒ [v] =
dx
dt
=
L
T
a =
d2x
dt2 =⇒ [a] =
d2x
dt2
=
L
T2
這裡我們沿用大物理學家J. C. Maxwell (1831–879) 所建議, 以中括號[·] 代表一個物理量
的量綱(dimension)。這裡要提醒的是
L
T2 =
d2x
dt2
6=
dx
dt
2
=
L2
T2
同理高階微分
dkx
dtk
之量綱為
dkx
dtk
=
L
Tk , k = 1, 2, 3, · · ·
其他的導出量例如, (密度)、F (力)、P (壓力) 也可以化為這三個基本量的乘積。按定義, 密
度是單位體積之質量 = m
V , 所以 之量綱為
[ ] =
[m]
[V ]
=
M
L3
由牛頓第二運動定律F = ma , 所以F 之量綱為
[F] = [m][a] = MLT−2
牛頓著名的萬有引力定律
F = G
m1m2
r2 =⇒ [F] = MLT−2 = [G]
M2
L2
所以萬有引力常數G 之量綱為[G] = L3
MT2 , 它的值大約
G ≈6.6726 × 10−11米3/千克· 秒2
由此也可推測Kepler 行星第三定律: 行星距太陽的平均距離的立方與行星繞太陽週期的平方
成正比, T2 ∝ L3 。
另外壓力是單位面積所受的力P = F
A , 因此
[P] =
[F]
[A]
=
MLT−2
L2 = ML−1T−2
16 數學傳播33卷3期民98年9月
順便一提, 假設壓力P 是密度 的函數、P = P( ) , 則
dP
d
=
[P]
[ ]
=
ML−1T−2
ML−3 =
L
T
2
右式等於速度的平方! 在氣體動力學這項正是音速的平方
dP
d
= P′( ) = c2, c : (音速)
2.3. 無量綱(dimensionless)
無量綱(dimensionless) 的觀念在量綱分析是非常重要的。
2.3.1: 角度不具有量綱
按角度的定義(由圓弧來看) =
s
r
, s 是弧長、r 是半徑, 這兩者都是長度單位[s] =
[r] = L , 因此角度 是不帶有量綱的(Angle is dimensionless.)
=
s
r
=⇒ [ ] =
[s]
[r]
=
L
L
= 1
相同的概念也可推論圓周率 是不具有量綱、[ ] = [s]/[2r] = 1 。
圖1. [ ] = [s]/[r] = 1 圖2. [sinA] = [a]/[c] = 1.
2.3.2: 三角函數不具有量綱
由三角函數之定義, 所有三角函數都是三角形邊長之CSqGSIb3DQ比例, 所以三角函數不具有量綱, 例
如
sinA =
a
c
=⇒ [sinA] =
[a]
[c]
=
L
L
= 1
2.3.3: 超越函數不具有量綱
超越函數(trancendental function) 例如ex、sinh x 此時[x] = 1 而且[ex] =
[sinh x] = 1 , 這個觀念對於處理Fourier 變換與Laplace 變換是非常重要的。
從量綱看世界17
3. 量綱平衡
量綱平衡(dimensional balance) 這是量綱分析最重要的原則, 一個具有物理意義的方
程式, 其等式兩端每一項的量綱必須一致, 凡是正確反映客觀規律的物理方程式, 其各項的量綱
(dimension) 都必須是一致, 只有方程式兩邊每一項的量綱都相同,方程式才可能成立。量綱平
衡背後的思想基本上是無量綱, 也是所謂無量綱化(nondimensionalization) 之根據。
3.1. 牛頓力學公式
s = v0t +
1
2
at2 =⇒ L =
L
T
T =
L
T2T2
v = v0 + at =⇒
L
T
=
L
T
=
L
T2T
讀者可以輕易的檢驗每一項都有相同的量綱。另外我們熟知的動能E 與(重力) 位能U 分別
是
E =
1
2
mv2, U = mgh =⇒ [E] = M
L2
T2 = M
L
T2L = [U]
因為動能與位能有相同的量綱, 因此可以相加減。
3.2. 單擺運動
學數學心裡一定要有例子(examples), 而不是定義、定理與證明。單擺運動是我個人最熟
悉的例子, 從方程的推導與各種解法甚至推廣至Hamiltonian系統, 我都是藉由單擺運動來想
像。單擺運動之周期公式; = 2
q
l
g , 可以藉由量綱分析兩邊比較單位
T = [] =
h
2
p
l/g
i
=
[l]
[g]
1
2
=
L
L/T2
1
2
= T
如此就不會將l
g
或g
l
混亂。我們藉單擺運動解釋量綱分析的使用方法, 已知的量及其量綱如
下:
單擺週期 [] = T
單擺長度l [l] = L
擺錘質量m [m] = M
重力加速度g [g] = LT−2
單擺角度 [ ] = 1
18 數學傳播33卷3期民98年9月
這裡有5個物理量, 但基本量有3個, 因此我們期待有5 −3 = 2 個無量綱的量, 因為單擺角度
1 = 不具有量綱, 我們還需要找到另一個無量綱的量, 透過左右配對量綱平衡的原則得
2 =
l
1
2 g−1
2
1, 2 這兩個無量綱的量可以有函數關係(functional dependent)
2 = p( 1) =⇒ = p( )
s
l
g
實際上p( ) = 2 , 歷史上第一位計算出這個值的是C. Huygens (1629-1695)。
圖3. 單擺運動
另外則是從方程式出發
d2
dt2 +
g
l
sin = 0 or
d2
dt2 +
g
l
= 0, ≪ 1.
由量綱平衡的原則得
[ ]
T2 =
g
l
[sin ] =
g
l
[ ] =⇒
1
T2 =
g
l
=⇒ ∝
s
l
g
透過量綱分析可以對物理推導過程進行檢驗, 它可以定性地表示出物理量與基本量之間的
關係; 可以有效地應用它進行單位換算; 可以用它來檢查物理公式的正確性, 確認是否一致無
誤, 甚至可以提供尋找物理現象某些規律的線索。學任何一門學問一定要有感覺, 因此我鼓勵讀
從量綱看世界19
者對於所學過的所有等式與(物理) 方程式都先利用量綱分析檢驗過, 並詢問各項所代表之物
理意義, 久而久之必可培養對物理與數學的直觀。
4. 幾何上之應用
4.1. 畢氏定理
直角三角形△ABC 之邊長a、b、c 滿足關係式
a2 + b2 = c2
可以藉由量綱分析來證明。決定直角三角形△ABC 之面積Sc 只需要斜邊與另一個銳角, 我
們取斜邊c 與其中一個銳角- 為兩個參數
Sc = f(c, -)
已知角度- 是無量綱, 面積之量綱是長度的平方, 所以Sc/c2 是無量綱:
[Sc/c2] = 1 =⇒ Sc = c2 (-)
在歐氏空間 (-) = 常數。現在將△ABC 分割成兩個以a、b 為斜邊的直角三角形則Sa =
a2 (-)、Sb = b2 (-)
Sc = Sa + Sb =⇒ c2 = a2 + b2
在非歐氏空間 6= 常數, 畢氏定理當然不再是這個形式。
圖4. 畢氏定理a2 + b2 = c2
與畢氏定理直接關聯的是正弦定律與餘弦定律, 利用角度與三角函數是無量綱容易驗證這
兩個等式是量綱平衡
a
sinA
=
b
sinB
=
c
sin C
L
L0 =
L
L0 =
L
L0
20 數學傳播33卷3期民98年9月
c2 = a2 + b2 −2ab cosC
L2 = L2 = L2 = LLL0
4.2. Hero(Heron) 公式
已知任意三角形△ABC 三邊是a、b、c , 令s = 1
2 (a + b + c) , 則
|△ABC| = S =
p
s(s −a)(s −b)(s −c)
由量綱(因次) 分析的角度來看Hero(Heron) 公式是非常有趣且直觀。底下是美國物理學家
Richard Feynman(1918年5月11日∼ 1988年2月15日) 在中學時的想法。現在想像三角形
△ABC , 其中b、c 兩邊漸漸往a 邊壓, 當b+ c > a 時會形成一個三角形, 因此面積S > 0
, 當b、c 壓到與a 共線時, 即b + c = a 時, 面積S = 0 , 所以由因式定理推得b + c −a 會
整除S , 三角形三邊可以輪換, 因此c + a −b、a + c −b 也都會整除S 。三角形的面積S
並不隨a、b、c 之位置而改變, 所以任意置換(permutation) a、b、c 所得的面積始終是不變
的。因此由不變量理論, S 必有(a + b + c) 這個因式, 綜合以上分析與因式定理, 可以猜測
S = (a + b + c)(a + b −c)(b + c −a)(c + a −b)
但這是錯誤的! 為什麼? 假設L 是長度的單位。令[f] 表示f 之量綱(dimension) 或單位,
S 是面積, 所以[S] = L2 , 而其它量都是長度
[a + b + c] = [a + b −c] = [b + c −a] = [c + a −b] = L
顯然L2 6= L · L · L · L , 但是S 確實有這四個因式, 因此合理的猜想是右式要開根號, 所以
可以猜
S = k
p
(a + b + c)(a + b −c)(b + c −a)(c + a −b)
k 是一個待求之常數, 因此再以最熟悉的直角三角形三邊3、4、5帶入上式得6 = k√12 · 2 · 6 · 4
, 所以k = 1
4
整理得S =
p
s(s −a)(s −b)(s −c) 。
a + b > c a + b > c a + b = c
圖5. Hero(Heron) 公式
從量綱看世界21
4.3. Frenet-Serret 公式
令t、n、b = t × n 是空間上曲線之(單位) 切向量、(單位) 主法向量與(單位) 次法向
量(binormal), 顯然{t, n, b} 形成一右手法則系統並且滿足一階微分方程:
dt
ds
= n,
dn
ds
= − t + b,
db
ds
= − n,
其中s 是弧長(arc-length) 參數、 是曲率(curvature)、 是扭率(torsion)。曲率是切向
量對弧長的變化率 =
dt
ds
、扭率則是次法向量對弧長的變化率 =
db
ds
。因為[s] = L、
[t] = [n] = [b] = 1 , 所以Frenet-Serret 公式告訴我們曲率與扭率之量綱正是長度之倒數
[ ] = [ ] = L−1
從量綱的角度這也給了我們合理的解釋為何稱曲率(扭率) 之倒數為曲率半徑(扭率半徑)。
5. 量子力學
十九世紀, 科學家們普遍認為古典力學的理論已趨於完備,然而對於黑體輻射(black body
radiation) 存在現象, 卻無法用古典理論來解釋,對於黑體輻射所衍生的問題, 在科學家的努力
下漸漸揭開其神秘面紗, 在揭開其神秘面紗的同時也引領我們進入另一全新的領域—量子力
學。1895-1900年間普朗克(Max Planck) 為著解決黑體輻射問題, 從理論猜測得出一黑體輻
射公式, 普朗克的新公式中就含有一個新的自然常量。他給這個常量取名為作用量單位, 並以~
表示, 後來這個自然常量更名為普朗克常數, 並一直延用至今。普朗克常數取值為
~ ≈6.626 × 10−34焦耳·秒, 焦耳=千克·米2/秒2
5.1. Schr¨odinger 方程
量子力學之代表是Schr¨odinger 方程
i~
@
@t
= H , H = H∗(Hamiltonian)
左右兩邊比較量綱得普朗克常數~ 之量綱
[~] = [H][t] = M
L2
T2T = ML2T−1
所以~ 的量綱是[能量] × [時間] , 這個量與古典力學的作用量S 的量綱相同,
[~] = [S] = [作用量]
22 數學傳播33卷3期民98年9月
這是了解量子力學最重要的一步。其次, 由de Broglie 物質波之假設
=
~
p
(波長), =
E
~
(頻率)
其中p 是動量, E 是能量; 為何 是波長、 是頻率呢? 由量綱分析得
[ ] =
[~]
[p]
=
ML2T−1
MLT−1 = L
[ ] =
[E]
[~]
=
[E]
[E]T
=
1
T
正好與波長、頻率有相同之量綱, 但是更有趣的是 、 是波的特性, 而動量p 與能量E 則是
粒子行為, 兩者是透過普朗克常數~ 聯繫起來, 也就是說普朗克常數~ 是波—粒二象性的橋
樑(當尺度很小的時候)。
圖6. E. Schr¨odinger 1887-1961 圖7. W. Heisenberg 1901-1976
5.2. Heisenberg 測不準原理
海森堡測不準原理或不確定性是說: 在一個量子力學系統中, 一個粒子的位置和它的動量
不可被同時確定。位置的不確定性△x 和動量的不確定性△p 是不可避免的;
△x△p ≥
~
2
, △E△t ≥
~
2
位置x 與動量p 之乘積還有能量E 與時間t 之乘積都與普朗克常數~ 有相同之量綱
[△x][△p] = L(MLT−1) = ML2T−1 = [~]
[△E][△t] = (ML2T−2)T = ML2T−1 = [~]
從量綱看世界23
量子理論的不確定原理使得位置與動量或能量與時間同時量得之精確度有一個明確的限制。因
為無窮大尖銳的區域表示在空間和時間上有一個對位置或時間無限精確的測量, 因而動量或能
量必須完全的不確定。一個不清楚普朗克常數~ 意義的人絕對不瞭解量子力學。
5.3. 普朗克長度、質量、時間
廣義相對論有兩個自然常數: 光速c 與牛頓的萬有引力常數G , 量子力學則只有一個自
然常數: 普朗克常數~ 。有時物理學家喜歡以{G, c, ~} 取代長度、質量、時間做為基本單位。
例如透過量綱分析容易驗證
p
~G/c3 具有長度單位
hp
~G/c3
i
=
ML2T−1 L3
MT2
(L/T)3
1
2
= L
p
~G/c3 ≈1.62 × 10−35m 就是普朗克長度, 它包含有重力G 與時空c 的資料, 也包含了
量子之訊息~ , 任何嘗試調和這兩個理論的測量長度單位必然是普朗克長度。另外
p
~c/G ≈2.18 × 10−8kg 是普朗克質量
hp
~c/G
i
=
ML2T−1LT−1
L3M−1T−2
1
2
= M
而
p
~G/c5 ≈5.38 × 10−44sec 則是普朗克時間(就是光走過普朗克長度所需的時間!)
hp
~G/c5
i
= T
由上述三個自然單位組成的單位制, 人們稱為普朗克單位制(或自然單位制), 這是普朗克於19
世紀末(1899年) 領悟出來的。
圖8. Max Planck 1858-1947.
24 數學傳播33卷3期民98年9月
6. 分析與不等式
我們可以將量綱平衡之原則應用到不等式:
『任何兩個量必須具有相同的量綱才能比較大小。』
一個函數的微分、積分也是具有量綱
∇kf =⇒ [∇kf] =
[f]
Lk =
F
Z Lk
fdx =⇒
Z
fdx
= [f][dx] = FLn
我們以大寫F 代表函數f 之量綱, dx 是n 維測度代表體積, 所以[dx] = Ln , 積分符號
R
是
P
之變形不具有量綱(面積加面積還是面積1 + 1 = 1 !)。微分、積分之量綱有本質上的
差異:
『積分—量綱增加、微分—量綱減少。』
藉由量綱分析可以容易判斷瑕積分之範圍
Z
|x|>1 |x|−
dx ≈Ln−
(L → ∞) =⇒ n −
< 0
dx ≈Ln−
(L → ∞) =⇒ n −
< 0
Z
|x|≤1 |x|−
dx ≈Ln−
(L → 0) =⇒ n −
> 0
dx ≈Ln−
(L → 0) =⇒ n −
> 0
長度單位L 可大可小, 對有界區域需考慮L → 0 , 因為我們不希望有擁擠或集聚(concentration)
的現象也就是 -函數產生, 因此要求指數為正、n−
> 0 。對無窮區域此時相當於
> 0 。對無窮區域此時相當於
L → ∞ , 因為我們不希望無窮大產生, 因此指數必須為負、n−
< 0 。如果n−
= 0 , 則
< 0 。如果n−
= 0 , 則
積分不具有量綱(dimensionless)
Z
|x|>1 |x|−
dx
dx
= L0 = 1 (
= n)
= n)
所以這個積分會以對數函數的形式出現。
6.1. Gamma-Beta 函數
Gamma函數x) 與Beta 函數B(x, y) 定義為
x) =
Z
∞
0
e−ttx−1dt, x > 0
從量綱看世界25
B(x, y) =
Z 1
0
tx−1(1 −t)y−1dt, x > 0, y > 0
藉由量綱分析可以簡單地猜測為何Gamma 函數- x) 必須要求x > 0 而Beta函數-
B(x, y) 必須要求x、y > 0 。首先x) 之積分函數中有e−t , 所以無窮遠點∞ 沒有問
題, 我們只需要考慮有界區域
x) =
Z
∞
0
e−ttx−1dt ≈[t]x−1[t] = [t]x ([t] → 0) =⇒ x > 0
對B(x, y) 函數而言只需要考慮有界區域其中有問題的地方是t = 0、1
B(x, y) ≈[t]x−1[t] = [t]x ([t] → 0) =⇒ x > 0
B(x, y) ≈[t]y−1[t] = [t]y ([t] → 0) =⇒ y > 0
藉由量綱分析也可以簡單判斷高斯積分(Gauss integral)
Z
∞
−∞
e−ax2
dx =
r
a
, a > 0
必然有1 √a
這個量:
Z
∞
−∞
e−ax2
dx
= [x] =
1
[a]1/2 , [ax2] = 1
6.2. Laplace 與Fourier 變換
(1) 已知
> 0 則
> 0 則
L(t
−1) =
−1) =
Z
∞
0
t
−1e−stdt =
)s−
−1e−stdt =
)s−
L(e tt
−1) =
−1) =
Z
∞
0
t
−1e te−stdt =
)(s − )−
−1e te−stdt =
)(s − )−
因為e−st 是超越函數, st 必定是無量綱[st] = [s][t] = 1
Z
∞
0
t
−1e−stdt
−1e−stdt
= [t]
−1[t] = [t]
= [s]−
−1[t] = [t]
= [s]−
除了常數(無量綱) 之外, 冪函數t
−1 之Laplace 變換必定是冪函數s−
。同理第二個
−1 之Laplace 變換必定是冪函數s−
。同理第二個
Laplace 變換我們只需將[st] = 1 換為[(s − )t] = 1 , 函數乘e t 相當於其Laplace
變換做了平移變換s 7→ s − 。
26 數學傳播33卷3期民98年9月
(2) 已知0 <
< n 則
< n 則
Z
Rn |x|
−ne−ix· dx =
−ne−ix· dx =
2
n
n
2
2 )
n−
2 ) | |−
由量綱分析可以確信|x|
−n 之Fourier 變換必定是冪函數| |−
;
−n 之Fourier 變換必定是冪函數| |−
;
Z
Rn |x|−n+
e−ix· dx
e−ix· dx
= L−n+
Ln = L
= bL
Ln = L
= bL
−
= [ ]−
= [ ]−
[x ] = [x][ ] = LˆL = 1
6.3. H¨older 不等式
已知 ⊂ Rn、1 ≤ p、q ≤ ∞、1
p + 1
q = 1 且f ∈ Lp()、g ∈ Lq() 則
Z
|fg|dx ≤ kfkpkgkq
量綱分析可以簡單判斷為何需要1
p + 1
q = 1 :
Z
|fg|dx ≈[f][g]Ln, kfkpkgkq ≈[f]L
n
p [g]L
n
q =⇒ n =
n
p
+
n
q
所以1 = 1
p + 1
q
告訴我們的正是量綱平衡, 詳細的細節可參考數學傳播或相關的文章。幾乎所
有數學分析的不等式都是由H¨older 不等式或Cauchy-Schwarz 不等式再加上微積分基本定
理所組成, 在此鼓勵讀者對這些不等式花點硬功夫, 它(她) 給你的回報是難以想像的。
量綱分析是認識並研究複雜現象以及解決工程問題的重要工具, 她可以讓你有基本的世界
觀, 而這個世界觀提供了一個有意義的基礎以解釋你的感覺或其它的測量所得的資訊, 她提供
了最接近大自然的近似結果: 當我們在描述事物時, 實際上是在描述它們的量綱。筆者由這門學
問受益良多, 希望藉由這篇文章與讀者分享這份喜悅, 並期盼讀者進而對於方程式、不等式與數
學有更直觀的認識。
『我們可以說大門已經第一次對一種新方法而開, 這種新方法充滿了多種奇妙的結果,
將來會引起其他人的關注。』
—伽利略(1564 –1642) —從量綱看世界27
圖9. Galileo Galilei 1564-1642
交大應數研究所博士班吳恭儉與李信儀幫忙校稿並給了一些寶貴意見, 在此特別謝謝他們。
參考資料
1. G. I. Barenblatt; Scaling, Self-similarity, and Intermediate Asymptotics, Cambridge
Texts in Applied Mathematics, Cambridge University Press, (1996).
2. G. I. Barenblatt; Scaling, Cambridge Texts in Applied Mathematics, Cambridge Uni-
versity Press, (2003).
3. B. J. Cantwell; Introduction to Symmetry Analysis, Cambridge Texts in Applied Math-
ematics, Cambridge University Press, (2002).
4. 林琦焜: Cauchy-Schwarz 不等式之本質與意義, 數學傳播(中央研究院數學所), Vol. 93, 26-42
(2000)。
5. 林琦焜: 單擺運動, 數學傳播(中央研究院數學所), Vol. 106, 36–3, (2003)。
6. 林琦焜: 向量分析, 滄海書局, 2007。
7. 林琦焜: Riesz 位勢與Sobolev 不等式, 交通大學出版社, 2008。
—本文作者任教國立交通大學應用數學系—
加速度[编辑]
维基百科,自由的百科全书
 表示,在国际单位制中的单位为米每二次方秒(
表示,在国际单位制中的单位为米每二次方秒( )。加速度是速度矢量對于时间的变化率,描述速度的方向和大小变化的快慢。
)。加速度是速度矢量對于时间的变化率,描述速度的方向和大小变化的快慢。在经典力学中,牛顿第二定律说明了力和加速度成正比,這定律又稱為「加速度定律」。假設施加於物體的淨外力為零,則加速度為零,速度為常數,由於動量是質量與速度的乘積,所以動量守恆。在電動力學裏,呈加速度運動的帶電粒子會發射电磁辐射。
在本页面中会多次用到质点这一物理概念。简单地说,当被研究的运动物体的大小和形状不对实验造成影响或影响很小时,可以把这个物体抽象成一个有质量但不存在大小、形状的点。是一个理想化的物理模型。
简述[编辑]
简单地说,速度描述了位置是如何变化的,而加速度描述了速度是如何变化的。比如,水平地向前扔出一个物体,起初它的速度朝向正前,然而由於重力它开始在向前的同时向下坠落,即其速度改变了。这里改变物体速度的主要是地球的重力引起的重力加速度。加速度具有向量性质,即需要用大小和方向同时描述一个加速度。在光滑水平面上向前运动的物体,如果向左或向右施以力,即给予了不同的加速度,则其速度会发生变化(包含了速率及方向),然而向左的加速度和向右的加速度显然引起了不同的效果。同样,施力的大小不同,引起的加速度不同,最终的结果也不一样,亦可以從向量的加成性來看。作为一个矢量,加速度的叠加和分解分别遵循平行四边形法则和三角形法则。
具體而言,加速度描述的是速度随时间的变化率。需要注意的是,由于速度也是矢量,因此加速度不为零的物体速度的大小(称之为速率)也不一定会发生变化,实际上,如果加速度保持与速度垂直,速度大小就一直不会改变,同时方向一直改变。这种情况在生活中最常见的是圆周运动,比如在被拴在一端固定的线的另一端的一个小物体在线保持绷直时做的运动,又比如带电粒子在仅受静磁场的洛伦兹力
 时做的运动。
时做的运动。直线运动中的平均加速度、瞬时加速度[编辑]
设质点A呈一維运动, 时刻位于
时刻位于 处,经过
处,经过 时间后位于
时间后位于 处,则定义质点A在
处,则定义质点A在 时刻的瞬时速度(简称速度)为
时刻的瞬时速度(简称速度)为 表示位移對时间的一阶导数,在时间-位移图上表现为求斜率。
表示位移對时间的一阶导数,在时间-位移图上表现为求斜率。首先,定义
 时刻到
时刻到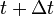 时刻之间的平均加速度为
时刻之间的平均加速度为 越小,该段时间内速度的波动就越小,描述的速度变化情况也就越精细,从而定义质点A在
越小,该段时间内速度的波动就越小,描述的速度变化情况也就越精细,从而定义质点A在 时刻的瞬时加速度为
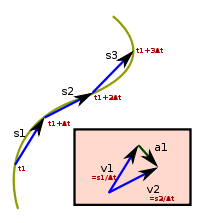
时刻的瞬时加速度为右图画出了三个质点在
 从坐标原点以相同的速度
从坐标原点以相同的速度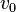 出发,由于分别拥有正、零、负的加速度而导致其位置
出发,由于分别拥有正、零、负的加速度而导致其位置 关于时间的曲线。可以将其想象为在光滑桌面上,三个木块以相同初速度,沿斜面向下、沿水平面、沿斜面向上滑行。
关于时间的曲线。可以将其想象为在光滑桌面上,三个木块以相同初速度,沿斜面向下、沿水平面、沿斜面向上滑行。在位移-时间图上,加速度由曲线的凹凸性表示,加速度为正的部分表现为凸函数,反之为凹函数,亦可以從微分的角度來分析。
曲线运动中的加速度[编辑]
设质点A在空间中运动,原点O指向A的矢量 为其矢径,则可类似定义其速度矢量和加速度矢量为[1]:24
为其矢径,则可类似定义其速度矢量和加速度矢量为[1]:24 并不趋于0)近似代替了微分,因此表现的是平均速度和平均加速度。可以看出,加速度与速度都具有方向和大小,并且即使在同一时刻两者方向也不一定相同。加速度与速度方向平行的分量表示速度大小的变化率(相同则加速,相反则减速),而与速度垂直的分量表示速度方向的变化率(速度矢量转动的角速度)。
并不趋于0)近似代替了微分,因此表现的是平均速度和平均加速度。可以看出,加速度与速度都具有方向和大小,并且即使在同一时刻两者方向也不一定相同。加速度与速度方向平行的分量表示速度大小的变化率(相同则加速,相反则减速),而与速度垂直的分量表示速度方向的变化率(速度矢量转动的角速度)。在
 足够小时,可以将那一小段曲线运动(称作元弧)近似看作直线运动或圆周运动。[1]:30
足够小时,可以将那一小段曲线运动(称作元弧)近似看作直线运动或圆周运动。[1]:30伽利略变换[编辑]
在经典物理下,即速度远小于光速、研究宏观物体时,可以使用伽利略变换来研究不同参考系间的加速度的联系,簡單來說就是座標間的轉換,但仍有保持一定的不變量[2]:32: 为物体在参考系
为物体在参考系 下的加速度,
下的加速度, 为物体在参考系
为物体在参考系 下的加速度,
下的加速度, 为参考系
为参考系 在参考系
在参考系 下的加速度。
下的加速度。考虑站在地面看火车上的人抛出一个小球,这个公式表达:小球相对于地面的加速度
 ,等于小球相对于火车的加速度
,等于小球相对于火车的加速度 加上火车相对于地面的加速度
加上火车相对于地面的加速度 。这个式子是矢量表达式,即三个加速度矢量的方向不在同一条直线上时,要使用矢量加法计算。
。这个式子是矢量表达式,即三个加速度矢量的方向不在同一条直线上时,要使用矢量加法计算。牛顿第二定律[编辑]
加速度最主要的应用之一是牛顿第二定律。简单地说,牛顿第二定律表明[2]:57,感受到合外力的作用,物体的加速度与合外力成正比,与质量成反比,加速度方向沿合力方向,在国际单位制中表示为 表示物体所受合外力,
表示物体所受合外力, 为物体质量,
为物体质量, 为物体的加速度。
为物体的加速度。在经典物理下,牛顿第二定律廣泛适用。此外,牛顿第二定律要求所处参考系为惯性参考系。 由于经典物理的研究几乎都会或多或少地涉及到物体在力的作用下的运动,又由于牛顿第二定律和伽利略变换极具简洁性,所以,牛顿第二定律是經典動力學裏的重要基礎定律,質點運動亦然。
惯性力[编辑]
當帶質量物體加速時,慣性是物體維持原有運動狀態的傾向,慣性力是對於這傾向的衡量[3]。因為慣性力實際上並不存在,只有原本將該物體加速的作用力實際存在,因此慣性力又稱為假想力。更具體而言,根據牛顿第二定律, 是第
是第 個作用力,
個作用力, 是物體的加速度。
是物體的加速度。重新編排,可以得到
 ,這物體的動力系統滿足方程式
,這物體的動力系統滿足方程式惯性力在平日生活中其实很常见,例如,停止不動的火车突然向前方加速,则所有站立乘客都会向後方倾移,這便是惯性力效應,從另外一個角度而言也是為了提供乘客們有足夠的摩擦力來進行移動。
加加速度[编辑]
将位移對于时间进行一阶求导得到了速度,二阶求导得到了加速度。可能会想到,可以通过进行三阶求导来得到一个诸如加加速度的物理量。在工程学中经常需要用到加加速度,特别是在交通工具设计以及材料等问题[5]。交通工具在加速时将使乘客产生不适感,这种不适感不仅来自于加速度,也与加加速度有关。在这种情况中,加速度反应人体器官在加速度運動時所感受到的力(见牛頓第二定律),加加速度则反应这作用力的变化快慢。较大的加加速度将会使人体产生相当的不适感,例如在电梯升降,汽车、火车等加速和转弯的过程中(在这些情况中加速度和加加速度的效应一般会同时存在)。人體需要時間適應加速度的變化,假若加加速度超過安全標準,則可能會發生像車禍造成的頸部扭傷(whiplash)一類的人體傷害。因而在设计交通工具时加加速度是必须考虑的因素。
在物理學裏,加加速度现在主要应用在混沌理论領域[6][7]。
角加速度[编辑]
角加速度涉及繞著固定轴轉動的物体,例如,想象一个圆盘和一个垂直固定於其中心的木棍,两隻手合拍住木棍并前後磨擦,造成木棍與圓盤共同轉動(例如,在地上高速旋转的陀螺,绕著固定点轉動)。在圆盘上做一个标记(如一条半径),则繞著固定轴轉動的物体可以简单地用标量角弧(即该标记转动的角弧)來做定量描述。旋轉運動可以與直线运动相类比:位移、速度、加速度,分别对应於角弧、角速度、角加速度。直线运动中已有的定律和方法可以直接带入,用於旋轉運動,例如,使用已有的匀加速直线运动理论来研究匀角加速度固定轴转动。[2]:249
在国际单位制中,角加速度的单位为弧度每二次方秒(
 )。其定义式为
)。其定义式为 為物體角加速度,
為物體角加速度, 为物体角速度,
为物体角速度, 为物体转过的角弧。
为物体转过的角弧。加速度的分解[编辑]
处理关于空间加速度矢量的问题,除了直接计算矢量之外,更多的时候可以将加速度按照适当坐标轴分解,即将矢量形式的加速度表示为相互独立的不同方向上的标量的形式。因为标量的计算要容易很多,因此这是解决问题常用的方法。按坐标系分解[编辑]
平面直角坐标系[编辑]
在平面直角坐标系中, 分别为x、y坐标轴上的单位矢量,皆为常矢量。
分别为x、y坐标轴上的单位矢量,皆为常矢量。这种分解方式的优点在于,形式简便,思维简单;因为单位矢量不会变化,故质点在二个方向上的投影等价于直线运动,并将其叠加,使得问题完全化为代数问题,并且可以直接使用直线运动的已有结论[2]:18。
极坐标系[编辑]
在二维空间裡,极坐标系用半径坐标 、角坐标
、角坐标  来表示質點的位置。半径坐标是極點与質點的直线距离;角坐标是極點与質點的连线对於极轴的角弧。在任意点的两个单位矢量分别为沿半径向外的
来表示質點的位置。半径坐标是極點与質點的直线距离;角坐标是極點与質點的连线对於极轴的角弧。在任意点的两个单位矢量分别为沿半径向外的 和垂直于半径指向角坐标正方向的
和垂直于半径指向角坐标正方向的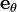 。不論是直角坐標或是極座標都可以互相來駔變換,座標與座標之間有一定的轉換量,使用以方便所在的坐標系為主。
。不論是直角坐標或是極座標都可以互相來駔變換,座標與座標之間有一定的轉換量,使用以方便所在的坐標系為主。從极坐标
 和
和  可以计算出直角坐标:
可以计算出直角坐标: 、速度
、速度 、加速度
、加速度 分别为
分别为按自然坐标系分解[编辑]
假設一個質點移動於二維平面。在質點軌道的任意位置,二維自然坐标系的一个坐标轴方向(切向)保持与軌道切線方向平行,另一个坐标轴方向(法向)則與軌道法線平行。分解按右图。向量可以無限地做拆解,所以只需要選擇對於分析最有利的為主!通常以切線方向和法線方向來分解。简单地说,加速度的切向分量
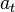 表示速度大小的变化,加速度的法向分量
表示速度大小的变化,加速度的法向分量 表示速度方向的变化,即
表示速度方向的变化,即 为此时刻的速度大小,
为此时刻的速度大小, 为此时刻的曲率半径。[2]:24
为此时刻的曲率半径。[2]:24按功能分解[编辑]
匀速圆周运动 向心加速度[编辑]
若质点以不变的速率(速度大小)沿著圆周繞著圆心运动,则质点呈匀速圆周运动,质点具有向心加速度 ,其方向保持沿半径方向向裏(因此不断变化),大小为
,其方向保持沿半径方向向裏(因此不断变化),大小为 是角速度。
是角速度。這公式也可以从极坐标系分解中,代入与匀速圆周运动相关的特殊值得到。更一般的情况下(非匀速圆周运动),以矢量来表示,
假设,在一根绳子的一端系上一个小物体(比如石頭),另一端握在手中,大致保持手不动而水平旋转,则手会明確地感受到绳子的拉力,该拉力的反作用力在绳子的另一端表現為向心力,提供小物体的向心加速度。当转得越快,向心力会越大,可以定性地验证上述向量式。从这个实验,可以看出,向心加速度总是使物体趋向于朝著圆心做运动;如果没有绳子施予向心力,物体一定会飞奔出去。
再舉一个例子,在游乐场的巨大旋转圆盘上,大部分遊客都會站立不稳,总是会向外摔倒,這是因為缺乏向心力施予於遊客。在旋转圆盘的非惯性系中,遊客會感受到慣性力,但由於缺乏向心力,無法達成平衡狀態,因此被向外“甩”出去,[4]:96-100這慣性力又稱為离心力,人们以这个原理制成了离心机。
上述公式不但對於从匀速圆周运动成立,也可以應用於各种圆周运动、甚至任意曲线运动,只是上述的
 和
和 应理解为该时刻的瞬时物理量,
应理解为该时刻的瞬时物理量, 应以曲率半径
应以曲率半径 替代,表示的是物体的加速度在垂直于路径方向的分量。
替代,表示的是物体的加速度在垂直于路径方向的分量。科里奥利效应[编辑]
舉例而言,設想一个巨大的圆盘在地上绕著定點匀角速度轉動(定點運動),而這定點為圆盤的圆心,在圆盘上沿半径方向有一个直导轨,一个物体被限制在导轨上运动,从圆心匀速向外移动。從地上(固定參考系)觀察,物體的軌跡不是一条直线,而是一条弧形或者螺旋形路线,物体也會感受到導軌的約束力,其方向垂直於導軌,並且指向圆盘旋轉方向(不是角速度向量的方向),這約束力促使物體朝著圆盘旋轉方向加速,使物體的軌跡呈弧形或螺旋形。從圓盤(旋轉坐標系)觀察,物體所感受到的科里奥利力會與導軌施予的約束力相抵消,因此,物體只會呈直線運動。假若,導軌不存在,則物體會逆著圆盘旋轉方向以科里奥利加速度運動。
在科里奥利效应裏,参考系S'的物體的柯里奧利加速度與感受到的科里奥利力分別為[4]:100-103
 为科里奥利加速度,
为科里奥利加速度, 为参考系S'在参考系S中的角速度矢量,
为参考系S'在参考系S中的角速度矢量, 为物体在参考系S'中的速度矢量。
为物体在参考系S'中的速度矢量。在气象学裏,科里奥利力使得熱帶氣旋在沒有強引導氣流影響下移向兩極。[8] 熱帶氣旋靠近兩極部分含有東風,科里奥利力會將東風拉向兩極;靠近赤道部分含有西風,科里奥利力會將西風拉向赤道。在地球上越接近赤道科里奥利力會越弱,所以科里奥利力影響熱帶氣旋靠近兩極部分會較靠近赤道部分為多。因此,在沒有其他引導氣流抵消科里奥利力的情況下,北半球的熱帶氣旋一般會向北移動,而南半球的熱帶氣旋則會向南移動[9]。
科里奥利力也會開啟氣旋系統的旋轉,但驅動高速度旋轉的主要因素,不是科里奥利力,而是凝結熱[10]。
欧拉力[编辑]
給定固定参考系S與旋轉参考系S',從固定参考系S觀察,旋轉参考系S'以非勻角速度 轉動。從旋轉参考系S'觀察,物體因這非勻角速度而感受到的虛設力(fictitious force)稱為「歐拉力」,產生的加速度稱為「歐拉加速度」。歐拉力
轉動。從旋轉参考系S'觀察,物體因這非勻角速度而感受到的虛設力(fictitious force)稱為「歐拉力」,產生的加速度稱為「歐拉加速度」。歐拉力 與歐拉加速度
與歐拉加速度 之間的關係式為
之間的關係式為欧拉加速度的一般公式为[4]:100-103
 是物體在旋轉参考系S'的位置。
是物體在旋轉参考系S'的位置。欧拉力为[4]:100-103
几种特殊的运动[编辑]
以下为几种特殊的运动,因为在不同的模型下质点常被不同地近似处理,并且可以得出的结论较之上面的积分式常能极大地简省计算量,故有研究的价值。最常運用的就是拋體運動,以及自由落體。匀速直线运动[编辑]
若某质点保持加速度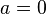 ,则其速度
,则其速度 的大小和方向不会变化,质点将保持在同一直线上以同一速率(速度大小)运动,这种运动被称作匀速直线运动。特殊地,若速度
的大小和方向不会变化,质点将保持在同一直线上以同一速率(速度大小)运动,这种运动被称作匀速直线运动。特殊地,若速度 ,则质点静止。
,则质点静止。匀速直线运动主要出现在牛顿第一定律中,该定律表示:“不受任何力或受合力为零的物体作匀速直线运动。”由于自然界中大部分力的随距离增大而减小,故离所有其它物体足够远的某一物体的运动能够在足够的精度下被近似为匀速直线运动。这种近似常被用于寻找惯性参考系和粒子物理学的运算当中。
匀变速直线运动[编辑]
若某作质点作直线运动并保持加速度 恒定,则质点作匀变速直线运动。在这种情况下,若
恒定,则质点作匀变速直线运动。在这种情况下,若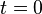 时刻速度为
时刻速度为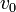 ,
,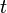 时刻速度为
时刻速度为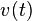 ,位移为
,位移为 ,则可由上面积分式得出
,则可由上面积分式得出自由落体运动 重力加速度[编辑]
自由落体运动是指初速度为0,加速度恒为竖直向下 [11] 的重力加速度g的运动,在地球上大约有 [12]。自由落体运动是匀变速直线运动的一种特殊情况。自由落体运动是将地球上的物体下落的状况进行理想化的抽象模型,当物体在地面附近,且所受空气阻力远小于其重力时,在一定精度内可被视作自由落体运动。
[12]。自由落体运动是匀变速直线运动的一种特殊情况。自由落体运动是将地球上的物体下落的状况进行理想化的抽象模型,当物体在地面附近,且所受空气阻力远小于其重力时,在一定精度内可被视作自由落体运动。加速度恒定的运动[编辑]
加速度是一个矢量,因此“加速度恒定”暗示加速度的大小和方向都不随时间变化。当加速度
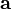 与速度
与速度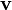 不在同一条直线上时,选取适当的坐标系,可以将其按照平面直角坐标系分解,使质点的运动在其中一个坐标轴上的投影为匀速直线运动,另一个方向上为匀变速直线运动。根据独立作用原理,两者的合运动(即质点的轨迹)为一条抛物线的一部分。
不在同一条直线上时,选取适当的坐标系,可以将其按照平面直角坐标系分解,使质点的运动在其中一个坐标轴上的投影为匀速直线运动,另一个方向上为匀变速直线运动。根据独立作用原理,两者的合运动(即质点的轨迹)为一条抛物线的一部分。抛体运动[编辑]
抛体运动具体包括平抛运动和斜(上、下)抛运动,和自由落体运动类似,它是在地球上向不同方向抛出的物体在忽略空气阻力的情况下的运动状况进行理想化的抽象模型。物体拥有一个非竖直方向的不为零初速度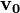 ,和竖直向下、大小恒定为重力加速度g的加速度,落地前的轨迹为一条抛物线的一部分。这也正是抛物线名字的由来。
,和竖直向下、大小恒定为重力加速度g的加速度,落地前的轨迹为一条抛物线的一部分。这也正是抛物线名字的由来。简谐运动[编辑]
再一个例子是简谐运动,即质点在正弦或余弦函数形式下的一维运动,一般形式为 为振幅,
为振幅, 为角频率,
为角频率, 为初相位。将其对时间求导后可得出
为初相位。将其对时间求导后可得出加速度的应用[编辑]
电磁辐射[编辑]
加速度的另一个重要应用之处是带电粒子的电磁辐射(即手机和收音机使用所需要的信号来源)。通过对麦克斯韦方程组的研究,可以将带电粒子产生电磁辐射的规律概括性地定性总结为:带电粒子的加速度产生电磁辐射,并且电磁辐射的强度和加速度大小正相关[13]。电磁辐射常见于用带电粒子的碰撞实验中。这类实验的一个早期著名例子是卢瑟福用电子碰撞金箔的实验,这个实验导致了对原子结构的深入探索。而这类实验至今广泛见于在各种大型粒子對撞機中,带电粒子以很高的速度运动,经受撞击后变慢、静止甚至反弹回来,这个过程中显然速度发生剧烈改变,一定经受了加速度不为零的过程,也一定会放出辐射。这样产生的辐射被称为轫致辐射。加速度产生电磁辐射的另一个很典型的例子是回旋加速器(回旋辐射)。带电粒子在回旋加速器中作圆周运动,每半圈加速一次,同时运动半径增大从而形成螺旋轨道,最后以很高的速度射出。圆周运动需要向心加速度来维持,当速度相当高时,加速度太大以至于因为电磁辐射损失的能量过多,导致回旋加速器实际对粒子的加速作用有上限。光速可比拟时,这时因为相对论效应而需使用同步加速器。这样产生的光能量高、偏振高,并且集中在一个很小的锥角里(相对论效应导致的前灯效应),因此是很好的大型物理用同步輻射光源。
狭义相对论[编辑]
狭义相对论用于速度可以和光速相比拟时的运动,并且要求参考系是惯性系。在狭义相对论中,加速度的定义没有改变。然而,由于在狭义相对论中,不同的参考系有不同的时间和空间度量标准,即当前参考系中的加速度为当前参考系中的位移对当前参考系中的时间的二阶导数,因此在参考系变换(洛伦兹变换)时变得复杂很多。设有两个参考系
 、
、 ,在空间直角坐标系中,三个坐标轴相对应平行,在
,在空间直角坐标系中,三个坐标轴相对应平行,在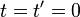 时刻两坐标系原点对齐,在
时刻两坐标系原点对齐,在 中
中 以速率
以速率 沿x正方向运动。
沿x正方向运动。同一事件在两个参考系中的時空坐標
 、
、 變换如下:
變换如下: .
.
 标示该物理量是在
标示该物理量是在  下的测量,
下的测量,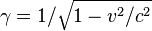 是勞侖茲因子,用
是勞侖茲因子,用 表示一质点的速度,
表示一质点的速度, 表示其加速度。表示定义式如下
表示其加速度。表示定义式如下 .
.
通过展开,可以得到[14]
 .
.
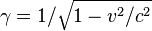 是勞侖茲因子
是勞侖茲因子可以看出,在狭义相对论中,加速度的变换公式冗长而复杂,各分量的公式也极不相似。再加上如果要考虑到力,虽然
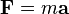 仍然成立,但质量也会变得随参考系的不同而不同。以上原因导致加速度在牛顿力学中那种因为简洁而具有的优越性,在狭义相对论中不复存在,必須使用更有功能的數學工具,即張量分析[2]:501。
仍然成立,但质量也会变得随参考系的不同而不同。以上原因导致加速度在牛顿力学中那种因为简洁而具有的优越性,在狭义相对论中不复存在,必須使用更有功能的數學工具,即張量分析[2]:501。广义相对论[编辑]
在广义相对论中和在量子力学中,大都是从能量、动量等的角度出发(类似于分析力学),而很少会像牛顿第二定律一样涉及到作用力;实际上,即使在需要表示出“位移的二阶导数”这一个量的时候,会趋向于直接使用 ,等价于
,等价于 ,来求解微分方程。因此,加速度在进階理论中較少被用到。
,来求解微分方程。因此,加速度在进階理论中較少被用到。运用到加速度的其中一个例子是等效原理,简单地说[2]:523。,它叙述了观测者不能在局部的区域内分辨出由加速度所产生的惯性力或由物体所产生的引力。比如,观测者站在地球上静止的电梯厢中向前方抛球,球会向下坠落,是因为地球的引力;而在远离任何星体的宇宙中的一个电梯厢,在以重力加速度
 向上(定义观测者踩到的地面为下)加速运动时,观测者抛出一个球,仍然会向“下”坠落,是因为惯性力。作为在封闭电梯厢中的观测者无法分辨这两种情况,爱因斯坦据此提出,引力与惯性力等价。等效原理是广义相对论中的支柱性原理之一。
向上(定义观测者踩到的地面为下)加速运动时,观测者抛出一个球,仍然会向“下”坠落,是因为惯性力。作为在封闭电梯厢中的观测者无法分辨这两种情况,爱因斯坦据此提出,引力与惯性力等价。等效原理是广义相对论中的支柱性原理之一。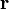 表示;而其大小則用
表示;而其大小則用 來表示。
來表示。





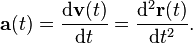






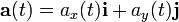
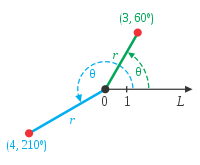
 、點
、點  的坐標分別以綠色、藍色展示。
的坐標分別以綠色、藍色展示。



![\mathbf{a} =\left[ \frac{d^2 r}{dt^2}- r \left( \frac{d\theta}{dt} \right) ^2 \right] \mathbf{e}_r + \left( 2 \frac{dr}{dt} \frac{d\theta}{dt} + r \frac{d^2 \theta}{dt^2} \right) \mathbf{e}_\theta.](http://upload.wikimedia.org/math/9/2/6/92648d7deccef6138cae8b5f3ec89988.png)


 後,单位矢量
後,单位矢量 、
、 。
。 ,
,
![\begin{align}
\mathbf{a} & =\frac{d \mathbf{v}}{dt} \\
& = \frac{d }{dt}\left( r \frac{d\theta}{dt} \mathbf{e}_\theta \right) + \frac{d }{dt} \left( \frac{dr}{dt} \mathbf{e}_r \right)\\
& = r \frac{d\theta}{dt} \frac{d\mathbf{e}_\theta}{dt}+ r \frac{d^2 \theta}{dt^2} \mathbf{e}_\theta + \frac{dr}{dt} \frac{d\theta}{dt} \mathbf{e}_\theta + \frac{d^2 r}{dt^2} \mathbf{e}_r + \frac{dr}{dt} \frac{d \mathbf{e}_r}{dt} \\
& =- r \left(\frac{d\theta}{dt}\right)^2 \mathbf{e}_r+ r \frac{d^2 \theta}{dt^2} \mathbf{e}_\theta + \frac{dr}{dt} \frac{d\theta}{dt} \mathbf{e}_\theta + \frac{d^2 r}{dt^2} \mathbf{e}_r + \frac{dr}{dt} \frac{d\theta}{dt}\mathbf{e}_\theta \\
& =\left[ \frac{d^2 r}{dt^2}- r \left( \frac{d\theta}{dt} \right) ^2 \right] \mathbf{e}_r + \left( 2 \frac{dr}{dt} \frac{d\theta}{dt} + r \frac{d^2 \theta}{dt^2} \right) \mathbf{e}_\theta \\
\end{align}](http://upload.wikimedia.org/math/e/0/d/e0d09e306831f39b0986e936584dd7a9.png)


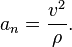



 ,极短时间
,极短时间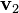 。因为是匀速圆周运动,速度大小保持为
。因为是匀速圆周运动,速度大小保持为 使用
使用 在
在 极小时近似于
极小时近似于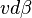 ,方向大约沿半径向裏,则该段时间内的平均加速度大小为
,方向大约沿半径向裏,则该段时间内的平均加速度大小为
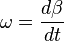 。
。 时精确成立。又因为
时精确成立。又因为








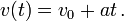




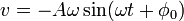




No comments:
Post a Comment