能否说明其物理意义,或者其作为数学工具的意义和目的?
按投票排序按时间排序
14 个回答
这个问题要先从一个工程师说起……
英国有一位工程师,名叫Heaviside(此君自学成才,化简了麦克斯韦方程组,提出了电离层假说),他使用了一种叫做“运算算子法”的计算方法来解决电路计算中的一些问题。
电路问题基本上就是微分方程的问题,所以这种方法现在依然用在解常微分方程中,举例来说:
定义算子:

这样一来一个微分方程比如,设r、e是关于t的函数:
r‘’+6r'+5r=e‘+3e
写成算子的形式就是:
(p+1)(p+5)r=(p+3)e [注1]
这样一来就相当于将微分和积分运算化为乘除,把微分方程化为代数方程,简单了很多[注2],现在常微分方程求解这也是一种常用而且比较简便的方法。
在电路分析中使用这种方法建立系统的数学模型也十分简便,而且电容电感可以写成等效容抗感抗值,之后写回路方程,按照Cramer法则求解即可。
这种方法虽然实用,却受到了数学家的质疑,因为缺少严谨的数学论证,后来人们在Laplace的著作中找见了可靠的依据,这种方法便被称为拉普拉斯变换法。
这种方法在电路的理论分析中的地位相当重要,后来CAD出现计算机也可以进行电路的分析,拉氏变的应用便逐渐减少,但拉氏变换建立起来的系统函数、零极点分析这样的概念却依然很实用:它可以直观的表现系统的输入输出特性。
与电路分析比较类似的还有连续线性是不变系统的分析。
数学和信号系统分析方面要先从Fourier变换说起……

此变换需满足Dirichlet条件[注3]:

而实际中有很多信号不满足狄利克雷条件,无法做出变换。
解决的方法是引入衰减因子 ,使得
,使得 满足狄利克雷条件,可以求出傅里叶变换。
满足狄利克雷条件,可以求出傅里叶变换。
这样做的物理意义相当于给一个振荡频率为 且震荡幅度不断增长的信号的幅度做了一个速率为
且震荡幅度不断增长的信号的幅度做了一个速率为 的衰减,如此一来便满足绝对可积条件。
的衰减,如此一来便满足绝对可积条件。
这样处理扩展了傅里叶变换使用的范围,并且将频域扩展为复频域,拉氏变换相当于在整个复平面上的变换,而傅氏变换仅仅是在这个复平面的虚轴上。
在系统分析中借助于基于拉氏变换的系统函数,可以从极点分布入手分析原信号波形、判断系统稳定性,也可以从零点分布入手分析时域函数的幅度和相位;也可以分析自由响应与强迫响应;更可以分析系统的频响特性[注4]。
倒是有一个自认为很好但很非主流的一个解释,复平面实际上不存在,对实际中能接触到的部分来说:
将C大九和弦一起摁发出的音符分解成 1 3 5 7 2这几个单音的过程实际上就是傅里叶变换,而乐谱则是音乐(时域)在频域上的分布。
把它推广到复平面,就需要拉氏变换了。
——
注1:
即赵博成提到的:“拉普拉斯变换首先是一个数学工具,在求解微分方程的时候起到巧妙的作用。”赵同学讲的基本正确,但缺少拉氏变换在信号系统分析中的应用
注2:
实际上这种使用算子的计算方法是有条件限制的,比如通常来说,消去律不成立。
注3:
周期信号与阶跃信号虽不满足这一条件,但因为冲击函数的存在其傅里叶变换依然存在。
注4:
与拉氏变换方法和概念都很类似的z变换也广泛应用在离散时间系统的分析中。
——
答主工科专业,数学功底比较糟糕,若有误谬,欢迎评论斧正 显示全部
英国有一位工程师,名叫Heaviside(此君自学成才,化简了麦克斯韦方程组,提出了电离层假说),他使用了一种叫做“运算算子法”的计算方法来解决电路计算中的一些问题。
电路问题基本上就是微分方程的问题,所以这种方法现在依然用在解常微分方程中,举例来说:
定义算子:
这样一来一个微分方程比如,设r、e是关于t的函数:
r‘’+6r'+5r=e‘+3e
写成算子的形式就是:
(p+1)(p+5)r=(p+3)e [注1]
这样一来就相当于将微分和积分运算化为乘除,把微分方程化为代数方程,简单了很多[注2],现在常微分方程求解这也是一种常用而且比较简便的方法。
在电路分析中使用这种方法建立系统的数学模型也十分简便,而且电容电感可以写成等效容抗感抗值,之后写回路方程,按照Cramer法则求解即可。
这种方法虽然实用,却受到了数学家的质疑,因为缺少严谨的数学论证,后来人们在Laplace的著作中找见了可靠的依据,这种方法便被称为拉普拉斯变换法。
这种方法在电路的理论分析中的地位相当重要,后来CAD出现计算机也可以进行电路的分析,拉氏变的应用便逐渐减少,但拉氏变换建立起来的系统函数、零极点分析这样的概念却依然很实用:它可以直观的表现系统的输入输出特性。
与电路分析比较类似的还有连续线性是不变系统的分析。
数学和信号系统分析方面要先从Fourier变换说起……
此变换需满足Dirichlet条件[注3]:
而实际中有很多信号不满足狄利克雷条件,无法做出变换。
解决的方法是引入衰减因子
这样做的物理意义相当于给一个振荡频率为
这样处理扩展了傅里叶变换使用的范围,并且将频域扩展为复频域,拉氏变换相当于在整个复平面上的变换,而傅氏变换仅仅是在这个复平面的虚轴上。
在系统分析中借助于基于拉氏变换的系统函数,可以从极点分布入手分析原信号波形、判断系统稳定性,也可以从零点分布入手分析时域函数的幅度和相位;也可以分析自由响应与强迫响应;更可以分析系统的频响特性[注4]。
倒是有一个自认为很好但很非主流的一个解释,复平面实际上不存在,对实际中能接触到的部分来说:
将C大九和弦一起摁发出的音符分解成 1 3 5 7 2这几个单音的过程实际上就是傅里叶变换,而乐谱则是音乐(时域)在频域上的分布。
把它推广到复平面,就需要拉氏变换了。
——
注1:
即赵博成提到的:“拉普拉斯变换首先是一个数学工具,在求解微分方程的时候起到巧妙的作用。”赵同学讲的基本正确,但缺少拉氏变换在信号系统分析中的应用
注2:
实际上这种使用算子的计算方法是有条件限制的,比如通常来说,消去律不成立。
注3:
周期信号与阶跃信号虽不满足这一条件,但因为冲击函数的存在其傅里叶变换依然存在。
注4:
与拉氏变换方法和概念都很类似的z变换也广泛应用在离散时间系统的分析中。
——
答主工科专业,数学功底比较糟糕,若有误谬,欢迎评论斧正 显示全部
不按人的认知规律出发,是教科书的普遍特点,导致读者理解困难。特别是拉普拉斯变换,应用领域太多,有人从信号理论第一次接触拉普拉斯变换,有人从控制理论,而有人从数理方程。这导致解释五花八门。
个人感觉从傅立叶这个人处理热传导方程讲起最符合认知论。在一个木棒上增加点热源,那么这个木棒的温度分布变化规律如何?人脑很自然的会以时间t作为变量大脑仿真这一过程,当然具体的数值还需要求解偏微分方程。解看起来很复杂,是一系列正弦函数的叠加。此时,如果将正弦函数叠加换个记号,不就方便了吗?这就是傅立叶变换。
拉普拉斯变换也是如此。
以上认知仅个人愚见,将拉普拉斯变换视为人类知识的一次“压缩”而非“拓展
”。很可能是错的,请有识之士指正。
个人感觉从傅立叶这个人处理热传导方程讲起最符合认知论。在一个木棒上增加点热源,那么这个木棒的温度分布变化规律如何?人脑很自然的会以时间t作为变量大脑仿真这一过程,当然具体的数值还需要求解偏微分方程。解看起来很复杂,是一系列正弦函数的叠加。此时,如果将正弦函数叠加换个记号,不就方便了吗?这就是傅立叶变换。
拉普拉斯变换也是如此。
以上认知仅个人愚见,将拉普拉斯变换视为人类知识的一次“压缩”而非“拓展
”。很可能是错的,请有识之士指正。
仔细研读过郑君里的信号与系统,曾经一度达到可以背诵上下两本书的程度。
后又熟读程佩青的数字信号处理,对其中的前八章达到背诵的程度。
最后有熟读奥本海默的信号与系统与离散信号处理两本书,这两本书实在是厚啊,总共1000+页!
楼上很多人都说拉普拉斯变换没有实际的物理意义,相对于傅立叶变换明确的物理意义来说,拉普拉斯变换只是一个算子。
这种说法未免有失偏颇。
首先承认拉普拉斯变换确实起到算子的运用,然而其物理意义长期没有被人发现。
简单的说,大家都认可傅立叶变换的本质是一个信号可以表示成正弦信号的叠加,即无法进行傅立叶变换。
大家如果注意到傅立叶变换与拉普拉斯变换的关系可以发现,当s=jw时,傅拉普拉斯变换便等于傅立叶变换。可见傅立叶变换是拉普拉斯变换的特例。那么重点来了,如果一个是增长型的,比如e^2t,这个信号指数增长,是无法表示成等幅的正弦信号的叠加的。注意,傅立叶变换的物理意义是一个信号可以表示成等幅的正弦信号的叠加!!
这个等幅的概念有多少人忽略了!!!
那么,推广一下,不等幅的正弦信号(e^at*sint)便出现了!
数学波形是很容易想象的。
回到e^2t的问题,这个信号无法表示成等幅的正弦信号的叠加(傅立叶变换),那么它为何不能表示成增幅的正弦信号的叠加呢?
这就是拉普拉斯变换的物理意义!!!
上面这个信号在拉普拉斯变换中有一个收敛域,s>2.复频域如何表示自行想象。
其意义是啥呢?
因为收敛域包括s=4这条纵轴,这就意味着这个信号可以表示成∑e^4t*sinkwt这种增幅信号的叠加形式。
因为收敛域包括s=5这条纵轴,这就意味着这个信号可以表示成∑e^5t*sinkwt这种增幅信号的叠加形式。
s=6,7,8等等,道理如上。
那么可以发现,在拉普拉斯变换的收敛域内有无数条纵轴,在每一条纵轴上都可以写成一个不等幅正弦信号的叠加。
从这个角度来看,傅立叶变换只不过是s=0纵轴上,信号分解成等幅(特别强调这个等幅概念)正弦信号的叠加。
拉普拉斯变换确实有些明确的物理意义,只不过大多人没发现罢了。
至于更详细的数学证明,未完待续。 显示全部
后又熟读程佩青的数字信号处理,对其中的前八章达到背诵的程度。
最后有熟读奥本海默的信号与系统与离散信号处理两本书,这两本书实在是厚啊,总共1000+页!
楼上很多人都说拉普拉斯变换没有实际的物理意义,相对于傅立叶变换明确的物理意义来说,拉普拉斯变换只是一个算子。
这种说法未免有失偏颇。
首先承认拉普拉斯变换确实起到算子的运用,然而其物理意义长期没有被人发现。
简单的说,大家都认可傅立叶变换的本质是一个信号可以表示成正弦信号的叠加,即无法进行傅立叶变换。
大家如果注意到傅立叶变换与拉普拉斯变换的关系可以发现,当s=jw时,傅拉普拉斯变换便等于傅立叶变换。可见傅立叶变换是拉普拉斯变换的特例。那么重点来了,如果一个是增长型的,比如e^2t,这个信号指数增长,是无法表示成等幅的正弦信号的叠加的。注意,傅立叶变换的物理意义是一个信号可以表示成等幅的正弦信号的叠加!!
这个等幅的概念有多少人忽略了!!!
那么,推广一下,不等幅的正弦信号(e^at*sint)便出现了!
数学波形是很容易想象的。
回到e^2t的问题,这个信号无法表示成等幅的正弦信号的叠加(傅立叶变换),那么它为何不能表示成增幅的正弦信号的叠加呢?
这就是拉普拉斯变换的物理意义!!!
上面这个信号在拉普拉斯变换中有一个收敛域,s>2.复频域如何表示自行想象。
其意义是啥呢?
因为收敛域包括s=4这条纵轴,这就意味着这个信号可以表示成∑e^4t*sinkwt这种增幅信号的叠加形式。
因为收敛域包括s=5这条纵轴,这就意味着这个信号可以表示成∑e^5t*sinkwt这种增幅信号的叠加形式。
s=6,7,8等等,道理如上。
那么可以发现,在拉普拉斯变换的收敛域内有无数条纵轴,在每一条纵轴上都可以写成一个不等幅正弦信号的叠加。
从这个角度来看,傅立叶变换只不过是s=0纵轴上,信号分解成等幅(特别强调这个等幅概念)正弦信号的叠加。
拉普拉斯变换确实有些明确的物理意义,只不过大多人没发现罢了。
至于更详细的数学证明,未完待续。 显示全部
拉普拉斯变换首先是一个数学工具,在求解微分方程的时候起到巧妙的作用。
而在不同的工科领域,其物理意义应该各有不同。例如在电路里面,若面对一个已经稳定的电路(无自由分量),可以对各种电路元件应用拉普拉斯变换,这样就不再关注元件的时域(不关注某一个时刻某个元件某个量的大小或者相位),把所有元件视为类似于电阻的东西,然后分析输入输出关系,求得传递函数。
在很多系统里面,拉普拉斯变换用于传递函数的求解,这可能是它普遍的物理意义。
而在不同的工科领域,其物理意义应该各有不同。例如在电路里面,若面对一个已经稳定的电路(无自由分量),可以对各种电路元件应用拉普拉斯变换,这样就不再关注元件的时域(不关注某一个时刻某个元件某个量的大小或者相位),把所有元件视为类似于电阻的东西,然后分析输入输出关系,求得传递函数。
在很多系统里面,拉普拉斯变换用于传递函数的求解,这可能是它普遍的物理意义。
拉普拉斯变换
 = \int_0^\infty f(t) e^{-st} \mathrm dt](http://zhihu.com/equation?tex=%5Cmathcal+L%5Bf%5D%28s%29+%3D+%5Cint_0%5E%5Cinfty+f%28t%29+e%5E%7B-st%7D+%5Cmathrm+dt)
这里变量 是一个复数,它没有明确的物理含义 —— 大部分物理量尤其是可观测量,譬如傅立叶变换中的频率
是一个复数,它没有明确的物理含义 —— 大部分物理量尤其是可观测量,譬如傅立叶变换中的频率 ,都是实数。
,都是实数。
傅立叶变换
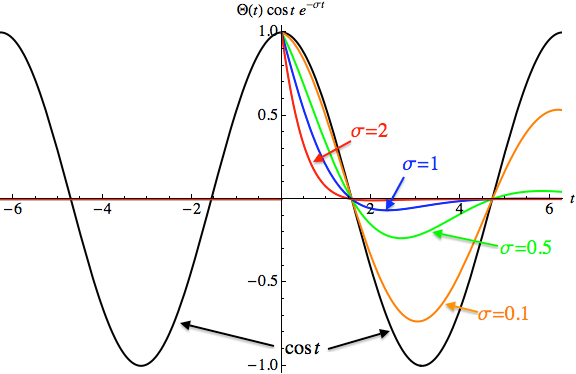
假如非要找到拉氏变换的含义的话,可以写成傅立叶变换来看: = \int_{-\infty}^{+\infty} \Theta(t) f(t) e^{-\sigma t} e^{-i\omega t} \mathrm dt \equiv \mathcal F[ \Theta(t)f(t) e^{-\sigma t} ](\omega)](http://zhihu.com/equation?tex=%5Cmathcal+L%5Bf%5D%28s%29+%3D+%5Cint_%7B-%5Cinfty%7D%5E%7B%2B%5Cinfty%7D+%5CTheta%28t%29+f%28t%29+e%5E%7B-%5Csigma+t%7D+e%5E%7B-i%5Comega+t%7D+%5Cmathrm+dt+%5Cequiv+%5Cmathcal+F%5B+%5CTheta%28t%29f%28t%29+e%5E%7B-%5Csigma+t%7D+%5D%28%5Comega%29)
换句话说,函数 的拉氏变换相当于将其
的拉氏变换相当于将其 的部分按照指数函数抽样以后的频谱。其逆变换,恰好是这些频谱的叠加。
的部分按照指数函数抽样以后的频谱。其逆变换,恰好是这些频谱的叠加。
信号:
实空间
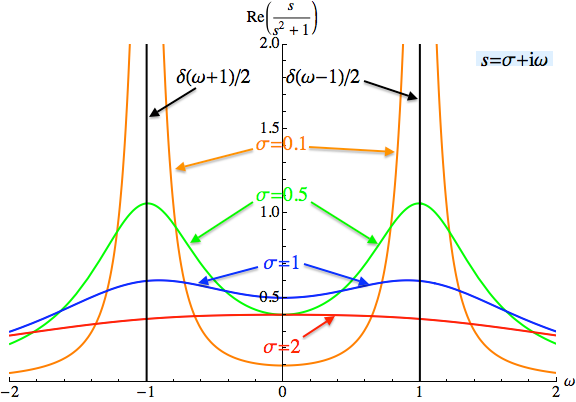
频谱空间(仅表现实数部分)
 显示全部
显示全部
这里变量
傅立叶变换
假如非要找到拉氏变换的含义的话,可以写成傅立叶变换来看:
换句话说,函数
信号:
实空间

频谱空间(仅表现实数部分)
 显示全部
显示全部
知乎用户 赞同
拉普拉斯变换的物理意义需要你懂一些统计力学,其中的指数乘子物理中往往表示耦合或者波尔兹曼分布的分布概率。统计力学中系综理论中经常求的配分函数其实就是做拉普拉斯变换,描述的是不同态之间按照各自权重进行求和的到的期望值。
首先发问:
先问题主,请问你对自己曾经开课的数学课程认真的学习过没有,是否曾经思考过这些数学公式后面对于客观世界的意义,即使没有明白甚至加深了困惑。就我学习过的数学课程来讲数学是在高度抽象的站点上来描述我们所在的这个客观世界运动变化规律的科学,是可以反复被实证的,这就是科学精神的所在之处。所以建议你不要讲数学“工具”。下面就我的学习和应用经历谈谈我仅对题主问题的理解,如果能对你有点帮助的话,那我就太开心了。
先说傅爷变换:
傅爷变换:1,是在e(jωt)的正交基函数上展开的,e(jωt)是变换的核函数;2,傅爷变换积分上下限是从-∞到+∞。天意冥冥,实函数(用于描述客观世界变化过程函数的必要条件函数)的傅爷变换是正负频率对称的,用两次欧爷公式:e(jωt)=cosωt+jsinωt,e(-jωt)=cosωt-jsinωt,这样一整,e(jωt)+e(-jωt)=2cosωt;实函数傅爷变换谱分析中是双边对称的,而且必须要合并正负频率项的,从而傅爷变换对于实函数(能描述我们客观世界变化的函数)就有了对应的物理意义,可分解为振动频率为ω的正弦波啊,(切记ω是圆频率,真正物理意义上频率是f=ω/2π,晕,π 这个牛牛牛常数掺和进来了)。否则傅爷变换中的负频率项咋整啊,没物理意义啊。如果你再看看帕塞瓦尔定理,这物理意义更是显而易见了,能量守恒了啊。物理学的能量守恒和咱这的能量守恒相比,虽然咱这儿借用了他们能量的概念,但是论最终的意义相比来讲那可是小巫见大巫的。
还有,通过傅爷变换从而有了随机过程中联系自相关函数和功率谱之间关系的维纳辛钦定理,这是功率谱估计最基本方法的基础,可以说在现代数字信号处理(基于随机过程信号)领域,维纳辛钦定理用傅爷变换这把锄头挖下去了第一个坑。
傅爷分析可粗浅的理解为将傅爷变换应用于线性时不变系统后,研究系统输入激励x(t):X(ω),系统函数h(t):H(ω)及输出响应y(t):Y(ω)三者间的关系,加上冲击函数和卷积公式,完美的一塌糊涂啊。
自此基于傅爷变换的傅爷分析打开了我们认知、分析和改造客观世界的另一个窗口-从时域分析到频域分析的思路转换,这个起点也是拉爷分析、调和分析、时频分析、小波分析以及泛函空间等等分析方法的滥觞。
再说拉爷变换:
拉爷变换与傅爷变换从纯数学角度看有两项不同:1,积分变换的核函数不一样;2,积分上下限不一样。对于学数学的一些牛哥来讲,这两个公式定义表达式不一样,显而易见,数学本就抽象,无需解释。对于像我这样从事工程技术的一般工程师们来讲,我们可以从下述内容做点工程应用上的解释:
傅爷变换的条件是被分析的函数必须在物理意义上能量有限,数学表达就是狄氏条件,绝对可积,间断点有限。但是绝对可积这个条件对于很多函数来讲太强了,从而很多描述客观世界变化过程的函数被挡在傅爷分析的大门之外,这咋行啊。e这个关乎宇宙的常数出来啦,e(at)这种自然指数函数是描述客观世界自然增长(a>0)或自然衰减(a<0)过程最合适不过的函数了(e这牛牛牛常数的名字也是因此而来的)。
傅爷变换是基于e(jωt)的,但是有些描述物理过程函数的能量不有限,咋整。简单,让这信号先衰减,我们看看衰减后能不能整傅爷变换。于是乎,基于傅爷变换的推广,拉爷变换诞生了s=σ+ωj,函数(或信号)x(t)拉爷变换等于0到+∞上x(t)对e(-st)=e(-(σ+ωj)t)的积分变换。刚才说过傅爷变换是在e(jωt)的正交基函数,s平面的虚轴上展开的,从而类比可以看出拉爷变换是在整个复平面上e(-st)核函数展开的。同时因为e(-st)=e(-(σ+ωj)t),复平面坐标下σ就是实轴,ωj是虚轴就是傅爷分析的频率。σ这项的引入就是e(-σt),就是给x(t)乘上一个多大的随时间自然衰减的量才使那些物理世界中能量无限的物理过程可以被傅爷分析搞定的,拉爷变换就是对x(t)乘以e(-σt)衰减项后在积分域0到+∞的傅爷变换。
还有一点就是拉爷变换中0到+∞上的积分上下限隐含了这是一个因果系统的,整个宇宙就是因果的(2011年有几个欧洲物理学家说发现超过光速有质量的粒子就是反因果律的,最后结果证明他们是错误的。这是必须的,如果这个世界不是因果的,那还有天理没有)。从e(jωt),e(-st),e(-(σ+ωj))到e(-σt)*e(-ωj)t,这里面的e和j真是太神奇了,所以如果时光倒流,而且假如我们能见到傅爷、拉爷他们,忽悠大谈崇敬之情时,他们可能会这么谦虚淡定的说到,“我们还行吧,那是因为我们站在了大牛欧爷和柯爷的肩膀上了,而欧爷和和柯爷又站在其他一群牛爷的肩膀上的”。
再回到开始,复习一下,拉爷变换与傅爷变换从纯数学角度看有两项不同:1,积分变换的核函数不一样;2,积分上下限不一样。第1项,由于引入了e(-σt)项从而使原来无法分析的信号也可以用傅爷分析了,并且引入判定被分析函数的收敛域,零极点,这可就是系统中的稳定性啊;第2项,0到+∞上的积分上下限蕴含了因果系统的必要条件,这可是数学模型可物理实现的前提啊,因果系统的必要条件是其系统时域冲击响应函数的定义域必须是从0开始的;而时域冲击响应函数的拉爷变换就是系统传递函数。拉爷变换中这两项不同正是为了将修正后的傅爷变换用于现实应用中的目的所在之处,太神奇了吧!!!
类似于傅爷分析,拉爷分析可粗浅的理解为将拉爷变换应用于线性时不变系统后,研究系统输入激励x(t):X(s),系统函数h(t):H(s)及输出响应y(t):Y(s)三者间的关系,加上冲击函数和卷积公式,完美的一塌糊涂啊。
有了上面关于拉爷变换的介绍,尤其e(-σt)和0到+∞上的积分上下限这两项的物理意义,在加上诸多描述客观世界变换规律的,难以在时域求解的微分方程,通过傅爷变换后化成s域的代数方程,求解后再逆变换成我们客观世界时域的解。在所以拉爷分析在控制(或系统)论中对于系统稳定性的分析以及在系统设计中的应用绝对是一把锋利无比的快刀,对于像我等这样的一般工程师来讲有此利刃在手,咱即使内功差点也可以仗剑行天涯了,相对原来可是强大的一塌糊涂了啊!工程系统设计中,要选择适当σ来保证系统是稳定(用数学讲就是收敛)的、是可物理实现(因果)的,至于零极点分析也是这个道理的。其实傅(拉)爷分析是像我这样的一般普通工程师的工程世界观基础的,一般工程世界里啥东东不都可以忽悠成:输入激励,系统,输出响应这三部分的;如果是控制,可能需要再加入一项反馈项,但是如果把反馈项再划到系统中变成一个新系统一起看,还是一样的。
离散域的说明:
至于DFS,DTFT,DFT,ZT都是计算机这伟大的机器诞生后由于应用的需要,是模数数模转换技术加计算机技术,让时间连续过程可离散化后(也可离散转连续)傅(拉)爷变换在时间离散域的对应形式而已(对于实际的模数过程,数字信号处理,还存在一个量化误差积累的问题)。但是必须要提的是,DFT和奈氏采样定理一起解决了时域有限采样点数据和频域有限点数据能够正确的完成傅爷变换表示的问题(其中意义相当牛牛牛的啊,要是没这,数字信号处理耍不动的!!!);同时FFT的出现是将傅(拉)爷变换的应用真正落到了实处。要说思想的话,这些离散域的变换都是基于傅(拉)爷变换基础之上的,如果你理解了傅(拉)爷变换,这些离散域变换的理解用数学证明一句常用说法,这是“显然”的,显而易见的。
附带讲述:
对于像我这样从事工程技术的普通工程师来讲,“输入激励,系统,输出响应”这个工程学世界观就是我们所见到的力学中的三个基本问题:1,知道系统和输出响应求输入,这是控制问题;2,知道输入激励和系统求输出,这是预测问题;3,知道输入激励,输出响应求系统,这是系统设计问题。我说的力学是指理论力学(各种常偏微分方程)、热统力学(宏观热传导方程,微观的各种分布)、电动力学(麦叔方程组)和量子力学(薛哥方程,波函数)四大力学;奥,忘记了,光学中还有个傅里叶光学了。这一下不就让傅(拉)爷分析来了个力学、热学、光学、电磁学和原子物理学各科大满贯通吃了。世界是运动变化的,整个宇宙都是振动的,这样一下,傅(拉)爷分析的应用可以无处不在啊!
至于这些具体学科中的物理意义自己去琢磨一下吧,用句数学方程上的术语来讲,通解都整给你了,特解你根据边界值的界定自己整整吧。钥匙都塞到你手里,哥们你就自己开开锁,进自己的家门吧!
所以对于大多数像我一样的晚辈们来讲,建议有牛人有机会去法国的话要拜拜这两位大牛爷的,代小弟上柱香。尤其类似于我这样的一般普通工程师们,现在整的好多东东其实是数十年甚至百年前物理学家耍过的试验,然后变成可重复的实验验证后,最后由我等集大成,利用其他众多工程前辈基础之上的当前工业技术把这些诸多“实验仪器”的诸多种功能融合到一起,变成可以工业化大规模生产的东东的。我不是说像我这样的小伙伴们干的事情没有创造性,只是讲,从思想(思路)上我们没有越过这些牛人前辈的。他们的思想就如同黑夜中一道闪电,瞬间照亮了像我一样的这些小伙伴们夜行在工程技术之路上前行的方向;闪电过后,即使黑暗继续,但我们可以依向而行,勇往直前。所以,我们尽可能的要以满怀敬重的态度来学习和思考这些前辈们的知识思想,从而才能有所继承和应用,如果能发扬那就再好不过了。
再提及一下:
傅(拉)爷分析是基于傅(拉)爷变换的一种分析方法,其中有众多科学家牛爷叔哥们和杰出工程师牛爷叔哥们的贡献的,绝对不可简单的等同于傅(拉)爷变换那两对四个公式,其中蕴意自己体会。
傅爷级数展开开始也不被同时代大牛们理解和接受(比如:另外一位拉爷,此拉爷非刚才上述的那个拉爷,但也是如雷贯耳的大牛爷的),原因很简单,凭直觉上就可以看到最早傅爷级数展开时存在的问题:正弦函数是连续的,对于有些有跳变间断点的函数(比如方波)你怎么去叠加了,才能保证在跳变间断点上也能表示了,如果不能表示那咋整。最后是狄氏给出了答案,就是现在狄氏条件,以及间断点如何收敛。所以对于像我这样的云云众位小伙伴们来讲,曾经难以理解傅爷级数(变换)的这种经历是必须的啊,但是这不能成为阻碍我们继承傅(拉)爷分析衣钵理想的借口。困难似弹簧啊,呵呵!
傅爷级数的思想是傅爷在研究热传导过程中,求解自己整出来的热传导偏微分方程,耍分离变量法时(这是求解常偏微分方程的最基本思想方法之一)引入的;他还破解过古埃及文,所以文史类里有个专家也叫傅里叶的,但和空想社会主义的傅里叶不是一个人,相同的是他们都是法国人,都姓傅里叶;傅爷忽悠过拿破仑,从过政,当过顾问以及警察局局长;不过傅爷当时任法兰西学院终身秘书时也曾经耽误过华哥。不怪傅爷啊,华哥你整的那群论在当时真是超前了,你往生之后,大牛刘叔看你文章也花了好几个月时间才理出点头绪的;还有可能就是,傅爷事务繁忙根本就没看到。再就是,假如要是华哥你、贝哥和图大叔不早点去见上帝,难道你们三个人要让上帝现身见你们不成,你们知道的太多了。
拉爷耍数学和力学不说了,地球人都知道啊!拉爷关于哲学中的机械唯物主义的思想有机会大家可以看看,对于像我这样的小伙伴们来讲可以开开眼界的。
我是一名从事工程技术的普通工程师,下面这句话是发自于我内心深处的,虽然对于有些从事数学物理以及其他学科的牛人们看来觉得有点搞笑,因为在科学之路上你们见到的大牛爷叔哥们太多了,他们可能只是你们学研之路上匆匆擦肩而过,一面之缘的路人,甚至他们其中有些人的肩膀就是你们落脚之处。但我是想让像我一样的其他这些小伙伴们再加深一下印象,我是绝对是满怀敬重的态度的。“傅爷,拉爷太谢谢你们了,晚辈我就拾了你们的点牙慧就可有向于行、民工于世,从而混口饱饭吃了。晚辈叩首了:咚,咚,咚!”
这么帅气,牛气和接地气的公式,必须用傅爷和拉爷最喜欢的浪漫花体作为变换作用符,而且必须要以最完美的对称形式写出来:
显示全部
先问题主,请问你对自己曾经开课的数学课程认真的学习过没有,是否曾经思考过这些数学公式后面对于客观世界的意义,即使没有明白甚至加深了困惑。就我学习过的数学课程来讲数学是在高度抽象的站点上来描述我们所在的这个客观世界运动变化规律的科学,是可以反复被实证的,这就是科学精神的所在之处。所以建议你不要讲数学“工具”。下面就我的学习和应用经历谈谈我仅对题主问题的理解,如果能对你有点帮助的话,那我就太开心了。
先说傅爷变换:
傅爷变换:1,是在e(jωt)的正交基函数上展开的,e(jωt)是变换的核函数;2,傅爷变换积分上下限是从-∞到+∞。天意冥冥,实函数(用于描述客观世界变化过程函数的必要条件函数)的傅爷变换是正负频率对称的,用两次欧爷公式:e(jωt)=cosωt+jsinωt,e(-jωt)=cosωt-jsinωt,这样一整,e(jωt)+e(-jωt)=2cosωt;实函数傅爷变换谱分析中是双边对称的,而且必须要合并正负频率项的,从而傅爷变换对于实函数(能描述我们客观世界变化的函数)就有了对应的物理意义,可分解为振动频率为ω的正弦波啊,(切记ω是圆频率,真正物理意义上频率是f=ω/2π,晕,π 这个牛牛牛常数掺和进来了)。否则傅爷变换中的负频率项咋整啊,没物理意义啊。如果你再看看帕塞瓦尔定理,这物理意义更是显而易见了,能量守恒了啊。物理学的能量守恒和咱这的能量守恒相比,虽然咱这儿借用了他们能量的概念,但是论最终的意义相比来讲那可是小巫见大巫的。
还有,通过傅爷变换从而有了随机过程中联系自相关函数和功率谱之间关系的维纳辛钦定理,这是功率谱估计最基本方法的基础,可以说在现代数字信号处理(基于随机过程信号)领域,维纳辛钦定理用傅爷变换这把锄头挖下去了第一个坑。
傅爷分析可粗浅的理解为将傅爷变换应用于线性时不变系统后,研究系统输入激励x(t):X(ω),系统函数h(t):H(ω)及输出响应y(t):Y(ω)三者间的关系,加上冲击函数和卷积公式,完美的一塌糊涂啊。
自此基于傅爷变换的傅爷分析打开了我们认知、分析和改造客观世界的另一个窗口-从时域分析到频域分析的思路转换,这个起点也是拉爷分析、调和分析、时频分析、小波分析以及泛函空间等等分析方法的滥觞。
再说拉爷变换:
拉爷变换与傅爷变换从纯数学角度看有两项不同:1,积分变换的核函数不一样;2,积分上下限不一样。对于学数学的一些牛哥来讲,这两个公式定义表达式不一样,显而易见,数学本就抽象,无需解释。对于像我这样从事工程技术的一般工程师们来讲,我们可以从下述内容做点工程应用上的解释:
傅爷变换的条件是被分析的函数必须在物理意义上能量有限,数学表达就是狄氏条件,绝对可积,间断点有限。但是绝对可积这个条件对于很多函数来讲太强了,从而很多描述客观世界变化过程的函数被挡在傅爷分析的大门之外,这咋行啊。e这个关乎宇宙的常数出来啦,e(at)这种自然指数函数是描述客观世界自然增长(a>0)或自然衰减(a<0)过程最合适不过的函数了(e这牛牛牛常数的名字也是因此而来的)。
傅爷变换是基于e(jωt)的,但是有些描述物理过程函数的能量不有限,咋整。简单,让这信号先衰减,我们看看衰减后能不能整傅爷变换。于是乎,基于傅爷变换的推广,拉爷变换诞生了s=σ+ωj,函数(或信号)x(t)拉爷变换等于0到+∞上x(t)对e(-st)=e(-(σ+ωj)t)的积分变换。刚才说过傅爷变换是在e(jωt)的正交基函数,s平面的虚轴上展开的,从而类比可以看出拉爷变换是在整个复平面上e(-st)核函数展开的。同时因为e(-st)=e(-(σ+ωj)t),复平面坐标下σ就是实轴,ωj是虚轴就是傅爷分析的频率。σ这项的引入就是e(-σt),就是给x(t)乘上一个多大的随时间自然衰减的量才使那些物理世界中能量无限的物理过程可以被傅爷分析搞定的,拉爷变换就是对x(t)乘以e(-σt)衰减项后在积分域0到+∞的傅爷变换。
还有一点就是拉爷变换中0到+∞上的积分上下限隐含了这是一个因果系统的,整个宇宙就是因果的(2011年有几个欧洲物理学家说发现超过光速有质量的粒子就是反因果律的,最后结果证明他们是错误的。这是必须的,如果这个世界不是因果的,那还有天理没有)。从e(jωt),e(-st),e(-(σ+ωj))到e(-σt)*e(-ωj)t,这里面的e和j真是太神奇了,所以如果时光倒流,而且假如我们能见到傅爷、拉爷他们,忽悠大谈崇敬之情时,他们可能会这么谦虚淡定的说到,“我们还行吧,那是因为我们站在了大牛欧爷和柯爷的肩膀上了,而欧爷和和柯爷又站在其他一群牛爷的肩膀上的”。
再回到开始,复习一下,拉爷变换与傅爷变换从纯数学角度看有两项不同:1,积分变换的核函数不一样;2,积分上下限不一样。第1项,由于引入了e(-σt)项从而使原来无法分析的信号也可以用傅爷分析了,并且引入判定被分析函数的收敛域,零极点,这可就是系统中的稳定性啊;第2项,0到+∞上的积分上下限蕴含了因果系统的必要条件,这可是数学模型可物理实现的前提啊,因果系统的必要条件是其系统时域冲击响应函数的定义域必须是从0开始的;而时域冲击响应函数的拉爷变换就是系统传递函数。拉爷变换中这两项不同正是为了将修正后的傅爷变换用于现实应用中的目的所在之处,太神奇了吧!!!
类似于傅爷分析,拉爷分析可粗浅的理解为将拉爷变换应用于线性时不变系统后,研究系统输入激励x(t):X(s),系统函数h(t):H(s)及输出响应y(t):Y(s)三者间的关系,加上冲击函数和卷积公式,完美的一塌糊涂啊。
有了上面关于拉爷变换的介绍,尤其e(-σt)和0到+∞上的积分上下限这两项的物理意义,在加上诸多描述客观世界变换规律的,难以在时域求解的微分方程,通过傅爷变换后化成s域的代数方程,求解后再逆变换成我们客观世界时域的解。在所以拉爷分析在控制(或系统)论中对于系统稳定性的分析以及在系统设计中的应用绝对是一把锋利无比的快刀,对于像我等这样的一般工程师来讲有此利刃在手,咱即使内功差点也可以仗剑行天涯了,相对原来可是强大的一塌糊涂了啊!工程系统设计中,要选择适当σ来保证系统是稳定(用数学讲就是收敛)的、是可物理实现(因果)的,至于零极点分析也是这个道理的。其实傅(拉)爷分析是像我这样的一般普通工程师的工程世界观基础的,一般工程世界里啥东东不都可以忽悠成:输入激励,系统,输出响应这三部分的;如果是控制,可能需要再加入一项反馈项,但是如果把反馈项再划到系统中变成一个新系统一起看,还是一样的。
离散域的说明:
至于DFS,DTFT,DFT,ZT都是计算机这伟大的机器诞生后由于应用的需要,是模数数模转换技术加计算机技术,让时间连续过程可离散化后(也可离散转连续)傅(拉)爷变换在时间离散域的对应形式而已(对于实际的模数过程,数字信号处理,还存在一个量化误差积累的问题)。但是必须要提的是,DFT和奈氏采样定理一起解决了时域有限采样点数据和频域有限点数据能够正确的完成傅爷变换表示的问题(其中意义相当牛牛牛的啊,要是没这,数字信号处理耍不动的!!!);同时FFT的出现是将傅(拉)爷变换的应用真正落到了实处。要说思想的话,这些离散域的变换都是基于傅(拉)爷变换基础之上的,如果你理解了傅(拉)爷变换,这些离散域变换的理解用数学证明一句常用说法,这是“显然”的,显而易见的。
附带讲述:
对于像我这样从事工程技术的普通工程师来讲,“输入激励,系统,输出响应”这个工程学世界观就是我们所见到的力学中的三个基本问题:1,知道系统和输出响应求输入,这是控制问题;2,知道输入激励和系统求输出,这是预测问题;3,知道输入激励,输出响应求系统,这是系统设计问题。我说的力学是指理论力学(各种常偏微分方程)、热统力学(宏观热传导方程,微观的各种分布)、电动力学(麦叔方程组)和量子力学(薛哥方程,波函数)四大力学;奥,忘记了,光学中还有个傅里叶光学了。这一下不就让傅(拉)爷分析来了个力学、热学、光学、电磁学和原子物理学各科大满贯通吃了。世界是运动变化的,整个宇宙都是振动的,这样一下,傅(拉)爷分析的应用可以无处不在啊!
至于这些具体学科中的物理意义自己去琢磨一下吧,用句数学方程上的术语来讲,通解都整给你了,特解你根据边界值的界定自己整整吧。钥匙都塞到你手里,哥们你就自己开开锁,进自己的家门吧!
所以对于大多数像我一样的晚辈们来讲,建议有牛人有机会去法国的话要拜拜这两位大牛爷的,代小弟上柱香。尤其类似于我这样的一般普通工程师们,现在整的好多东东其实是数十年甚至百年前物理学家耍过的试验,然后变成可重复的实验验证后,最后由我等集大成,利用其他众多工程前辈基础之上的当前工业技术把这些诸多“实验仪器”的诸多种功能融合到一起,变成可以工业化大规模生产的东东的。我不是说像我这样的小伙伴们干的事情没有创造性,只是讲,从思想(思路)上我们没有越过这些牛人前辈的。他们的思想就如同黑夜中一道闪电,瞬间照亮了像我一样的这些小伙伴们夜行在工程技术之路上前行的方向;闪电过后,即使黑暗继续,但我们可以依向而行,勇往直前。所以,我们尽可能的要以满怀敬重的态度来学习和思考这些前辈们的知识思想,从而才能有所继承和应用,如果能发扬那就再好不过了。
再提及一下:
傅(拉)爷分析是基于傅(拉)爷变换的一种分析方法,其中有众多科学家牛爷叔哥们和杰出工程师牛爷叔哥们的贡献的,绝对不可简单的等同于傅(拉)爷变换那两对四个公式,其中蕴意自己体会。
傅爷级数展开开始也不被同时代大牛们理解和接受(比如:另外一位拉爷,此拉爷非刚才上述的那个拉爷,但也是如雷贯耳的大牛爷的),原因很简单,凭直觉上就可以看到最早傅爷级数展开时存在的问题:正弦函数是连续的,对于有些有跳变间断点的函数(比如方波)你怎么去叠加了,才能保证在跳变间断点上也能表示了,如果不能表示那咋整。最后是狄氏给出了答案,就是现在狄氏条件,以及间断点如何收敛。所以对于像我这样的云云众位小伙伴们来讲,曾经难以理解傅爷级数(变换)的这种经历是必须的啊,但是这不能成为阻碍我们继承傅(拉)爷分析衣钵理想的借口。困难似弹簧啊,呵呵!
傅爷级数的思想是傅爷在研究热传导过程中,求解自己整出来的热传导偏微分方程,耍分离变量法时(这是求解常偏微分方程的最基本思想方法之一)引入的;他还破解过古埃及文,所以文史类里有个专家也叫傅里叶的,但和空想社会主义的傅里叶不是一个人,相同的是他们都是法国人,都姓傅里叶;傅爷忽悠过拿破仑,从过政,当过顾问以及警察局局长;不过傅爷当时任法兰西学院终身秘书时也曾经耽误过华哥。不怪傅爷啊,华哥你整的那群论在当时真是超前了,你往生之后,大牛刘叔看你文章也花了好几个月时间才理出点头绪的;还有可能就是,傅爷事务繁忙根本就没看到。再就是,假如要是华哥你、贝哥和图大叔不早点去见上帝,难道你们三个人要让上帝现身见你们不成,你们知道的太多了。
拉爷耍数学和力学不说了,地球人都知道啊!拉爷关于哲学中的机械唯物主义的思想有机会大家可以看看,对于像我这样的小伙伴们来讲可以开开眼界的。
我是一名从事工程技术的普通工程师,下面这句话是发自于我内心深处的,虽然对于有些从事数学物理以及其他学科的牛人们看来觉得有点搞笑,因为在科学之路上你们见到的大牛爷叔哥们太多了,他们可能只是你们学研之路上匆匆擦肩而过,一面之缘的路人,甚至他们其中有些人的肩膀就是你们落脚之处。但我是想让像我一样的其他这些小伙伴们再加深一下印象,我是绝对是满怀敬重的态度的。“傅爷,拉爷太谢谢你们了,晚辈我就拾了你们的点牙慧就可有向于行、民工于世,从而混口饱饭吃了。晚辈叩首了:咚,咚,咚!”
这么帅气,牛气和接地气的公式,必须用傅爷和拉爷最喜欢的浪漫花体作为变换作用符,而且必须要以最完美的对称形式写出来:

显示全部
电信系的路过,大学四年都在和这位大神打交道。拉氏变换(要读错成“拉*变换哟”)是数学中联系时域和频域的重要工具,起到类似作用的还有傅立叶变换和Z变换。通俗点讲就是生活中你看到的任何一个波,不论是什么形状都能被转换成频率成倍数关系的一系列波的特定组合,而在坐标轴中画出的这一系列波的频率和它们系数的关系(x轴标明频率大小,y轴标明频率对应系数的大小),这样就得到了原来那个波的频域曲线。将时域转换到频域可谓是波的研究中的及其基础又及其重要的内容,有了频域的图像就能通过一些滤波器,乘法器等等实现特定频率段波的过滤个频率的搬移,然后在物理学中通过对反射波和折射波频域的研究能得到很多物质的特性,通信中能够实现远距离和大量信息的低损耗传输。综上,拉氏变换是波的研究的重要工具。







No comments:
Post a Comment