兩重積分的定義,
從醉月湖的面積談起
向量微積分簡介 (第 5 頁) 蔡聰明 |
.原載於數學傳播第二十一卷第二期 .作者當時任教於台大數學系 ‧對外搜尋關鍵字 |
|
今想像有流體在管子中流動,其速度場為 這叫做流體的通量向量場 (the flux vector field of the flow)。因此,f(x) 表示單位時間流體通過 x 點處橫截面之通量 (flux)。由於
表示單位時間單位長度流體在 x 點處的減少量,亦即在 x 點單位時間單位長度流散出的量,因此叫做散度 (divergence)。按積分的定義可知, 顯然成立。這是一種散度定理。 上述流體的觀點,推廣到兩維平面恰好也就是 Green 定理(20)式的解釋。為了說明這件事,我們必須推廣(21)式。 在(21)式中,分母可改為矩形的面積,但是分子較難推廣,不過並不絕望。我們重新整頓一下 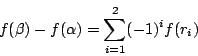 其中
其中
叫做向量場
按兩重積分的定義,
此式跟(20)式還有一段距離,不過我們可以證明
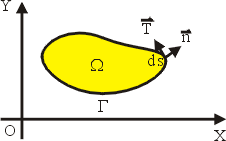
代入(24)式就得到法向式的 Green 公式了。 另一方面,在上述(23)式的定義中,其分子是沿邊界
換言之,
按重積分的定義,
我們也可以證明
代入(27)式就得到切向式的 Green 公式了。
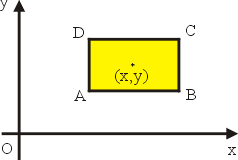
下面我們就來證明(25)與(28)兩式。 為了計算方便起見,我們作一矩形,以 (x,y) 點為中心,圍成領域 S,並且四邊跟 x 軸或 y 軸平行,參見圖15。設 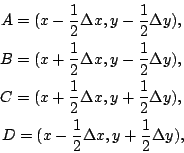 我們先證明(25)式。為此,必須估算流體流出 S 之通量。流體流出邊界 AB, CD, AD 與 BC 的通量分別約為 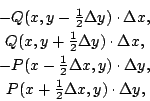 其中我們取四邊的中點當估值的代表點。因此,流出 S 的通量約為 ![\begin{eqnarray*}[P(x + {1\over 2}\!\Delta x,y)
- P(x - {1\over 2}\!\Delta x,y)]...
... {1\over 2}\!\Delta y)
- Q(x,y - {1\over 2}\!\Delta y)] \Delta x
\end{eqnarray*}](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img138.gif) 由平均變率定理 (Mean value theorem),這個通量為
其中 亦即 於是(25)式得證。 其次證明(28)式,仍然參見圖15。我們要估算流體沿邊界
其中 亦即 從而(28)式得證 雙重積分之應用
一、平面積
1. 卡式座標
(1) 求兩條曲線(
依雙重積分概念列出面積積分計算式:
其中
代入得計算式

(2) 求兩條曲線(
依雙重積分概念列出面積積分計算式:
其中
代入得計算式

2. 極座標
(1) 求一條曲線所圍面積
依雙重積分概念列出面積積分計算式:
其中
代入得計算式
(2) 求兩條曲線(
依雙重積分概念列出面積積分計算式:
其中
代入得計算式

二、曲面積(Surface area)
(1)空間曲面(Surface)S,其方程式為
其面積分式為
(2)設
則向量函數的面積分:
 
代回原曲面積分式,得
|


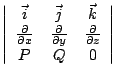
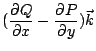
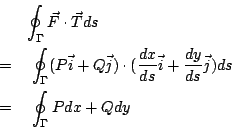


No comments:
Post a Comment