http://mooc.guokr.com/note/15930/
| qeff 华夏仙侠   注册日: 08-10-31 发表数: 6396 |
| ||||
人在三维空间中可以是静止的，但在四维时空中一直在旅行，因为时间一直在流逝。如果你的加速度为零，你的世界线就是直线。Week 8 Relativity and Black Hole 相对论和黑洞第8周
e的i次方 2015-01-28 23:54
8.1 Introduction 引入
上周留下了一个问题，如果中子星的质量超过了3倍太阳质量的极限以至于中子简并压力不能抵抗坍塌，会怎么样。为了解决这个问题，我们需要学习更多的物理学知识。
牛顿力学的相对性原理（principle of relativity）
伽利略1632年在他在对话中提到：如果你在一条船的封闭船舱中，做任意物理实验，都不能分辨船是抛锚静止的还是在平静海面上匀速前进的。不过伽利略并不知道这一问题之下的数学原理。
对于牛顿力学，公式F=ma几乎就是它的一切。无论相对于静止的参考系还是匀速直线运动的参考系，加速度a都是不变的。不过，对于速度v就不一样了，我们找不到一个绝对静止的参考框架，绝对静止是没有意义的。对速度而言，只有相对速度才是物理学问题。
Wiki 相对性原理：
http://zh.wikipedia.org/wiki/%E7%9B%B8%E5%AF%B9%E6%80%A7%E5%8E%9F%E7%90%86
本周内容：
首先跟随牛顿力学的相对性原理，看它能带我们走多远。
电磁学理论和牛顿力学相对性原理不一致，我们对牛顿力学做修正——狭义相对论（special relativity）。
牛顿引力（Newtonian gravity）仍然不一致，再次修正——广义相对论（general relativity）。
对于狭义相对论会有更多技术性介绍，会有计算；而对于更复杂的广义相对论，仅仅会介绍基本原理、结论。
最后我们会把这些知识运用到对黑洞的理解上。
从牛顿力学到相对论，我们可以看出科学理论是对真实的近似，科学的发展是不断接近真理的过程。从根本的哲学层面上，牛顿力学错了，但是在技术层面上，在适当的情形下，它依然得到了近乎正确的结果。广义相对论或许并不是最终答案，它可能仅仅是比牛顿力学更加精确的近似。
8.2 Spacetime 时空
讨论相对性原理，我们需要一个数学框架——时空（space-time）。
空间是某物可以存在的所有可能地方，我们生活在三维宇宙，所有可能位置都能被三个坐标轴上的数字标记r=(x, y, z)。
描述一个物体的运动，只需要让计时开始，在任意时间点上，计算三个坐标轴上的三个函数r(t)={x(t),y(t),z(t)}。时空是我们描述物体运动的地方。
把r(t)在坐标系中画出来叫做世界线（world line）。描述一维的运动，我们需要一个二维平面；描述二维的运动，我们需要一个三维空间；而描述一个三维运动，我们需要一个思维空间，我们在现实中找不到四维空间，不过我们可以在数学上描述它。
世界线是直线说明物体在做匀速直线运动，世界线是曲线说明物体在做变速（速度大小或方向改变）运动。在时空框架里，所有可能发生的事件（events）对应坐标(t, r)=(t, x, y, z).牛顿第一定律现在可以这样表述：不受力的物体在时空里的世界线是直线。
世界线的斜率（从时间轴t起算）表示了速度，下图中，很容易看出绿线代表的运动速度比红线代表的快。水平的世界线（橙色）表示一个静止的物体，竖直的世界线（蓝色）表示在某一固定时间点上的空间中所有地方。我们可以把t轴叫做此地（here，x=0），把x轴叫做此时（now，t=0）。
（伽利略）相对性原理在时空中的表现
现在，我们有另一个观测者（对应上图蓝色坐标系），它相对于黑色的坐标系以匀速v沿着x轴运动。在黑色观测者看来，这个观测者的世界线是一条倾斜的线（t’轴），不过对于蓝色观测者，他觉得t’轴才是他的“此地（here）”。
对于同一个事件，黑色观测者描述为（x, t），蓝色观测者描述为（x', t'）。两人的时间是同步的，所以显然t=t’。但对于空间坐标，由于两人的“此地”不一样，会有差异，x'=x-vt. 相应地t=t'，x=x+vt’.
那么对于速度u和u’呢？
对于同一个运动（上图绿线），如果蓝色观测者看来是x'=u't', 那么根据上面的结论，黑色观测者看来是x=x'+vt'=u't'+vt’=(u'+v)t'. 对比可知u=u'+v. 可见，两个惯性系的观测者都会对一个匀速直线运动做出匀速直线运动的判断，只是它们观测的速度相差了一个常数。不过两个惯性系之间无法区分，是蓝色相对黑色向右运动还是黑色相对蓝色向左运动？它们是等效的。
8.3 Maxwell and c 麦克斯韦和光速c
麦克斯韦的困惑
麦克斯韦根据测量得到的电磁场的一些性质量，利用麦克斯韦方程组算出电磁波的速度是光速c，c是一个和选定惯性系无关的不变量，并不像我们上节中提到的那样，在不同的惯性系中观测会发现速度相差一个常数。
两种解决方案
寻找以太的尝试
光钟（light clock）实验，假设以太存在，两个相距为L的镜子，如果它们相对以太参考系静止，那么左边镜子发出的光经过右边镜子的反射弹回到左边的时间T=2L/c. 当镜子相对以太运动时，时间会发生变化。
如果镜子相对以太向右运动，由于光相对于以太速度为c，那么光线从左到右的时间是L/(c+v)，同理已知反射后回到左边的时间是L/(c-v).
如果镜子向上运动
如上图，绿线代表光相对于镜子的运动，蓝线代表镜子相对于以太的运动，那么红线就是光相对于以太的运动，而光相对于以太速度为c，根据上图，由相应的几何关系，可得从一面镜子到另一面镜子的时间t，而总时间是t的两倍。
如果在地球上竖立这样两面镜子，随着地球围绕太阳做圆周运动，镜子和以太的相对速度会不断变化，光往返的时间T也会不断变化。1887年，迈克尔逊和莫雷（Michelson‐Morley）做了这样的实验，但是，他们并没有观测到时间T的变化。
为了拯救以太，有人提出了其他一些更加复杂的假说，例如以太会被有质量的物体拖曳，地球也会拖曳以太，这些可以解释迈克尔逊-莫雷实验的结果，但会和其他一些实验的结果相矛盾。
1905年，爱因斯坦（Einstein）提出了一个激进的观点——不存在以太，麦克斯韦方程对任意惯性系成立。伽利略的相对性原理是错误的。
8.4 Lorentz Transformations 洛伦兹变换
爱因斯坦的理论被迈克尔逊-莫雷实验和其它很多实验证实，下面我们需要应用光速c不变对伽利略相对性原理进行修正。
同样，我们假定两个参考系，黑色参考系（x, t）和蓝色参考系（x', t'）. x=t=0对应x'=t'=0，蓝色参考系相对黑色参考系匀速v向右（x轴正方向）运动。我们在x=t=0发射一个光脉冲，那么在黑色参考系里，光脉冲世界线为x=±ct（正负是因为光不仅仅传向一个方向），在蓝色参考系为x’=±ct’.
我们可以有
x'=Ax+Bt, t'=Cx+Dt
A, B, C, D是待定系数，因为要保证时空均匀性，所以变换式一定是线性（一次）的。
当x'=0时，即对于蓝色参考系的“此地”，一定有x=vt.
把这种情况带入上面的第一个方程，0=Avt+Bt，所以B=-Av.
类似的，当x=0时，x'=-vt'.
把这种情况带入上面的两个方程，-vt'=Bt，t'=Dt，所以B=-Dv.
于是，我们可以把之前的变换式做如下改写：
x'=A(x-vt), t'=Cx+At
下面利用光速不变，把x=ct和x'=±ct'都带入上式，
ct'=A(ct-vt), t'=Cct+At
可得出t'=A(c-v)t/c, t'=(Cc+A)t
所以A(c-v)/c=Cc+A，解出C=-Av/c^2.
现在只需要解出A就行了，A一定是v的函数，我们记为A(v)，现在变换式表示如下：
我们可以把x，t反解出来，同时注意到运动的相对性，蓝色坐标系相对黑色坐标系匀速向右运动等同于黑色坐标系相对蓝色坐标系相对黑色坐标系匀速向左运动，于是我们又如下等式：
分子项可以约掉，现在关键问题A(v)和A(-v)这两个系数的关系，我们的宇宙并不会区分左右，空间是同质的，所以A(v)=-A(v). 这样，我们可以解出：
于是，我们得到伽利略变换式修改后得到的伦伦兹变换式：
分析伦伦兹变换式可以知道，当v<<c且x不是很大时，洛伦兹变换式几乎等同于伽利略变换式。
8.5 Relativistic Spacetime 相对论时空
首先回顾一下我们假定的几个事实：
（1）如果A相对B速度是v, 那么B相对A的速度是-v.
（2）在一个惯性系里匀速直线运动（不受力）的物体，在另一个惯性系看来也是匀速直线运动。
（3）在所有的惯性系里观测到的光速是一样的。
根据上面三个假设我们推出了洛伦兹变换式，对于洛伦兹变换式，我们需要注意的是v不能大于c，否则式子会变得没有意义，超光速是无法达到的。下面我们开始应用洛伦兹变换得出狭义相对论（special relativity）的结论。
此外说明一点，我们的空间是三维空间，如果y轴、z轴方向没有运动，那么y'=y，z'=z.
同时的相对性（relativity of simultaneity）
这是一个非常反直觉的结论，当t'=0时，t=vx/c^2. 两个参考系的观测值时间不一样，只有x=0即他们在同一个地方的时候，时间才是一样的。
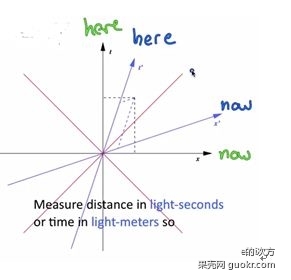
如上图，我们画出两个参考系的x轴、t轴，真正让我们惊讶的不是x轴和x’轴不重合，而是t轴和t’轴不重合。当同时成为相对的时候，因果律（causality）会失效吗？会出现悖论（paradoxes）吗？第8节我们会介绍2个佯谬。
关于上图的一些几何关系，如果我们改变t轴上的标尺，把上面的时间都乘以光速c，在这样的单位（借用长度单位表示时间，例如光在1s内走过的长度表示1s）下光速c=1. 这时，我们会发现x'轴和t'轴关于45°倾斜线对称。实际上对于任何观测者，x轴和t轴都关于这条斜线对称，记住这个几何关系，我们就可以不必费心去记洛伦兹变换表达式了。
还有一个问题，当我们说不同地方的两件事同时发生时，我们指的是什么？我们怎么能知道离自己很远的地方发生了什么呢？举个例子，如果现在，距离地球6000光年的蟹状星云发生一个事件，那么6000年后我们将能够在地球上看到它。如果现在t=0，我们所说的在距离x处的同时发生的事件就是指在t=x/c时将会到达我们这里的事件。
长度缩短（length contraction）
对于一个蓝色参考系中静止的尺子，它的头x1'=0，尾x2'=L'，显然它在蓝色参考系中长度为L’. 应用洛伦兹变换：
在t时刻，在黑色参考系中：
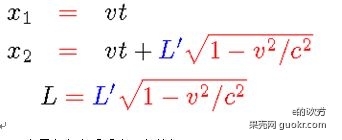
可见在黑色参考系看来尺长缩短了。
那么对于相对于黑色参考系中静止的尺子，在蓝色参考系看来会怎么样呢？同样是缩短，因为运动是相对的，大自然不会区分左右。
注：这里说明一下，有些人可能会把x1=0，x2=L带入上面的洛伦兹变换式算出x1'和x2'，然后会得出
. 实际上这里犯了一个错误。在你在测量一个物体长度的时候，如果这个物体是静止的，你可以在不同时刻读取始末点的读数，但如果这个物体是运动的，你就必须在同一时刻读取始末点的读数。现在，尺子相对于黑色参考系静止，你在黑色参考系的t时刻“同时”读出了尺子的始末点在蓝色参考系下的读数x1'和x2'，但注意这个“同时”是相对于黑色参考系的，对蓝色参考系而言，你读取x1'和x2'是“不同时”的，结果当然是错误的。这里如果想得出正确结果，应当使用洛伦兹逆变换公式，保证读取x1'和x2'在蓝色参考系（相对尺子运动的参考系）是同时的。
时间膨胀（time dilation）
在蓝色参考系x'=0处，我们选定两个时间点，t1'=0，t2'=T'，显然在蓝色参考系看来这个时段长度是T’. 应用洛伦兹逆变换公式：
可以得到在黑色参考系中：
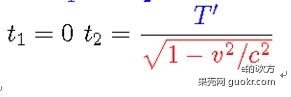
所以在黑色参考系看来这个时段长度T变长了：
同样由于相对性，对于黑色参考系中固定地点的一个时段，在蓝色参考系中看来也会变长：
所以，两个惯性系中的观察者都会觉得对方的时间比自己慢。
多普勒频移效应（Doppler）
因为时间膨胀效应，我们需要对之前的多普勒频移公式做出修正。
如果波源沿着切向（tangential）运动，之前我们说波长不变。但是由于时间膨胀，波的周期在我们看来变成了，于是频谱变小，波长边长（红移，red shift）。
如果波源沿着径向（radical）运动：
上面的结论是真实的吗？
我们做了很多实验来验证上面的结论，它们都是真实的。我们把金原子核加速到接近光速，会发现测得的尺寸变大了。对于高速运动的不稳定粒子，它的衰变期变长了。还有低速的实验，我们把原子钟放在喷气式飞机上做环球航行，回来之后发现飞机上的原子钟时间落后与一直停在原地的原子钟时间。
任何尺子在高速下都会缩短，任何钟表在高速下都会变慢，因为组成它们的材料都遵循洛伦兹变换的规律，它们基本上都是要靠电磁相互作用结合在一起的，它们必定遵循麦克斯韦方程组。实际上洛伦兹变换并不是爱因斯坦最先推导出的，而是洛伦兹最先推导出的，他起初并不接受爱因斯坦的相对论，他仅仅是在研究电磁场的时候发现电磁场看起来在它的运动方向被压缩了。
注：洛伦兹推出这个变换后，仅仅将其中的t'作为参量，他并没有敢说t’就是另一个惯性系中的时间。
新的速度相加规律
当v<<c，u<<c的时候，u≈u'+v，这正是伽利略变换的结果；
当u’=c的时候，无论v是多少，u=c，这就是说，在任意惯性系里，光速不变。.
8.6 Invariant Interval 不变间隔
利用洛伦兹变换式，我们可以得到一个不变量s^2：
我们可以把它画在时空坐标系里，如下图两条红线，实际上这两条线代表光速运动物体的世界线：
我们叫它光锥（light curve），因为对于二维空间加一维时间组成的坐标系，红线将会变成两个圆锥，圆锥把整个空间分成三部分（两个s^2<0的区域是两在一起的）。
光锥内部：s^2>0
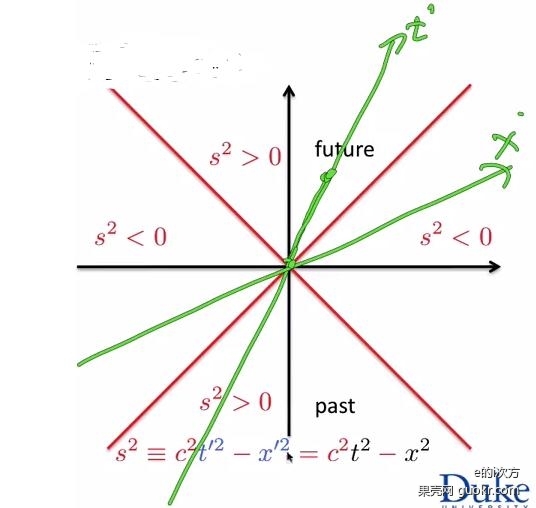
光锥内部被分为两个区域，上方的未来（future）和下方的过去（past）。
在x'=0(绿色参考系的此时)上，我们选两个事件，一个对应时间0，一个对应时间t’，我们有
，这个量叫本征时间（proper time，图上两个绿点的距离），它是在相对于本地静止的参考系看来，两个事件的时间间隔。
世界线只能在光锥内部，光锥内部的所有点都可以通过小于光速的速度与当前事件建立因果联系。
光锥外部（s^2<0）
因为速度不可能超过光速，光锥外部的线不可能是世界线。对于光锥之外的直线，我们无法找到一个惯性参考系，让它表示“此地”，不过我们可以找到一个惯性参考系，让这条线代表“此时”，这条线代表这一惯性系里所有同一时刻发生的事件的集合。
在t'=0（绿色参考系的此地）上，我们选择两个点，一个是0，一个是x’，我们发现
，这个量叫本征距离（proper distance），这是相对于事件发生地静止的观测值观测到的距离，他会认为这两件事同时发生。
现在我们再假定第三个观测者——蓝色观测者（x'', t''），他的相对于黑色观测者的速度比绿色观测者更快。我们现在观察两个事件，一是图中所有线的交点，这一事件对应所有观测者相遇，另一个事件是绿线x''轴上的蓝点。对于这两个事件，绿色观测者会认为它们是同时的（时间t'=0），但是蓝色观测者会认为蓝点事件对应的时间为负值（t''<0），它发生在相遇之前。从这里可以看出，光锥外部的点是无法和原点建立因果联系的，因为在不同的观测者看来，它既可能发生在原点事件之前，也可能发生在原点事件之后。例如，如果相遇时间导致了蓝点事件，那么在绿色观测者看来，结果事件居然比原因事件更早发生，这显然是矛盾的。所以，不仅仅粒子速度不能超光速，信息的传播速度也不能，否则就会造成结果事件更早发生的悖论。
8.7 Conservation Law 守恒律
在伽利略变换之下，动量p=mv和动能E=mv^2/2是守恒的，当然在不同惯性系的观测者看来，一个体系的动量和能量可以不一样，但是当一个观察者发现在某一过程中动量和能量的改变量为0时，另一个观测者必定也会认为改变量为0。但是，上述动量和能量的定义在洛伦兹变换下不守恒，我们需要做如下修正：
~
~
观察相对论动量的表达式，如果我们每次设法是物体增加一个相同的动量Δp，那么物体的速度不断增大，
会趋于无穷大，所以速度v的增加会越来越小，它永远都不会超过光速c。实际上有人把叫做相对论质量（本课程的老师并不喜欢这样的定义，所以下面说的质量都是指本征质量）。
观测相对论能量的表达式，它和我们原先定义的关系不容易看出来，低速下近似之后可以看出它比原先定义多了mc^2，如果质量守恒的话，mc^2是不变的，我们主要关系在一个过程里能量的改变量，所以加一个整体偏移没有影响。不过在某些核反应里，质量并不守恒，减少的质量会转化成能量。
在相对论框架下，E^2-p^2*c^2=m^2*c^4是一个与运动无关的不变量，我们可以利用这个来定义不变质量（invariant mass）。
（E, c^2*p）在洛伦兹变换中的表现和（t, x）是一样的。
这些守恒律总是成立的，拉瓦锡（Lavoisier）1777年做燃烧实验的时候如果能测量得更精确一些，他会发现质量不是守恒而是稍微减少了一点，一个燃烧会发光发热，一部分质量变成能量。当然，燃烧过程是原子尺度下的电磁相互作用，释放能量比较小，质量亏损很少。如果是原子核尺度的强相互作用，释放能量巨大，质量亏损将变得可测。在衰变中，也会有质量亏损和能量释放。
其他守恒律——电荷数守恒、电子数守恒，这些和观察者的参考系无关，所以仍然成立。
电磁相互作用、核相互作用都能找到洛伦兹不变量，后来我们还找到了它们的量子版本（quantum relativistic version）——量子场论（quantum field theory），那么引力相互作用呢？牛顿引力中的伽利略变换不变量在洛伦兹变换下不是不变量，爱因斯坦花了10年的时间来解决这一问题。
8.8 Simultaneity Paradoxes(optional) 同时的佯谬（可选）
1.梯子佯谬（the ladder paradox）
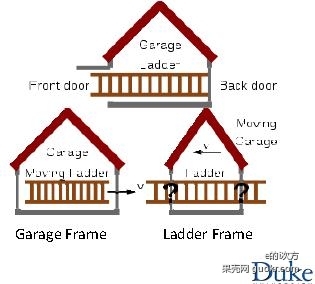
如上图，一个梯子的本征长度是L，车库的本征长度是G，L<G，显然梯子不能放进车库。但是如果让梯子告诉运动，根据相对论尺缩效应，一定可以让梯子短到小于G，即
. 此时，在车库所在的参考框架看来，梯子可以放进车库；但是，在梯子所在的参考框架看来，它的长度并未变化，相反车库缩短了，梯子更加不可能放进车库了。我们能不能关掉车库的前后门，在车库参考系看来似乎可以，在梯子参考系看来似乎不可以，不同参考系对同一事件的看法出现矛盾了吗？
答案当然是没有矛盾，我们来具体分析一下，我们把用车库参考系表示的事件记为(t, x), 把用梯子参考系表示的事件记为(t’, x’). 我们现在把梯子的左端放在车库左端的位置，把这一点作为位置原点。则
, 
, 
, 
, 而
.
实际上，我们需要考虑两个事件，事件1是梯子的左端和车库的左端在同一点上，事件2是梯子的右端和车库的右端在同一点上，问题的关键在于这两件事发生的先后顺序。
对于事件1，
, 
. 对于事件2，我们有
, 
，利用洛伦兹变换公式
，我们有
，可见在车库参考系看来，当0≤t≤t_2的时候，梯子的确完全在车库内部。利用洛伦兹逆变换
，我们有
，在梯子参考系看来，事件2先于事件1发生，梯子从来没有完全在车库内部。对于车库参考系，我们的确可以在一段时间了将车库的左右门同时关上，但是这在梯子参考系看来并没有同时，车库的左门关上之时车库的右门已经打开了。
下面我们用另一种方式——时空图再看一遍这个问题。
如果用图来解决这个问题，我们可以看得更加直观，黑色是车库参考系，蓝色是梯子参考系。注意和x轴平行的是车库参考系的等时线，和x’轴平行的是梯子参考系的等时线。
有一件事需要提醒，对于一个事件(t, x)，我们需要在ct’轴、x’轴上找出读数(t’, x’)，需要注意的一点是这张图不同于欧式几何，距离
并不表示任何含义，它并不是洛伦兹变换中的不变量，比如说，ct’轴上某一点在黑色坐标系下与原点的欧氏距离并不表示它在ct’轴上的读数。
洛伦兹变换的不变量是
, 故
对于ct’轴，我们有x’=0，而x=vt,所以
，所以
，t’<t，如果看欧氏距离的话会得出t’>t的错误结论。对于x’轴，我们有t’=0，这条轴上的点和原点连线的斜率是速度的倒数（注意时间轴是ct而不是t），所以
, 则
, 
所以
. X’轴和ct’轴的标尺如上面右图，可见欧式距离和x轴与ct轴不一样，所以在这一点上，图具有一定的误导性。
我们回到梯子问题，
左图表示了两个事件在车库参考系上的时间，t
，它发生在事件1之后。右图表示了两个事件在梯子参考系上的时间，
，它发生在事件1之前。
另外我们可以继续问一下如果在事件2发生的同时，车库的右门被关上了会怎么样。
显然，梯子的右端的运动被车库停止了，那么梯子的左端会立刻停止吗？不会，它必须等到右边的信号产生的波传播到左端。这个波的速度和梯子的材料有关，不过它是一个有限量，不会超过光速，我们假定它的速度就是光速，在上图中和光锥垂直的红线就代表信号波的传播。我们可以发现当信号波到达左端的时候，即使在梯子坐标系里，事件的时间也大于0了，此时梯子的确完全在车库内，不过这时梯子必定发生形变了。如果梯子足够好没有被破坏，它可能会被弹回去而恢复原来形状。
2.双生子佯谬（twin paradox）
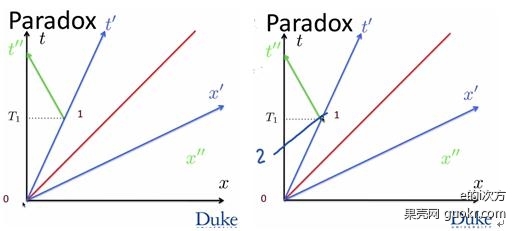
我们假定一对双生子在地球上生活了一段时间，他们是同龄的。现在双生子1留在地球，而双生子2乘飞船离开，一段时间后返回，那么他们还是同样年轻吗？双生子2的运动如上左图，匀速行驶一段时间后再匀速返回，转折点是事件1。
我们先来分析前半段，这一段到事件1为止。在事件1的地方，双生子1的时间是T_1，但是在双生子1看来，双生子2此刻的时间
, 
，所以他觉得双生子2的时间过得比自己慢，双生子2更年轻。但是，在旅行中的双生子2看来，此刻的概念不一样，它会觉得与事件1同时的不是T1，而是上面右图中画出的时间2，它表示的时间在双生子2看来是
，他会觉得双生子1比自己年轻。这里没有任何问题，因为运动是相对的，狭义相对论的结果一定具有这样的对称性。
事件1之后的匀速运动和事件1之前的效果一样，那么当双生子2回到地球的时候，就应该有
，双生子2比双生子1更年轻！但是根据狭义相对论的原理，在同地他们的时间应该是同步的，在这里我们发现狭义相对论的对称性被破坏了。为什么会这样呢？
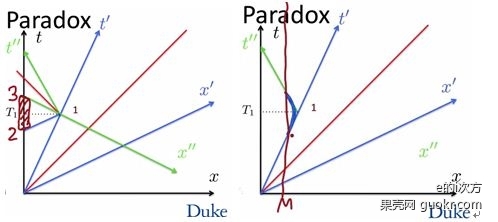
实际上我们刚刚忽略了一件事，那就是事件1发生的瞬间，双生子2速度发生变化，他非惯性了，而双生子1一直是惯性的，所以他们的对称性就是在这一刻被破坏的。在一个瞬间发生速度变化，加速度瞬间达到无穷大，这不合实际，不过却让问题变简单了。如上方左图，飞船转向发生前，双生子2认为的双生子1那里的同时对应事件2，但飞船转向发生后双生子2认为双生子1那里的同时对应事件3，由于转向是瞬间完成的，这是一个突变。事件2和3之间的时间差就是双生子2回到地球之后他们年龄的差距。这里狭义相对论的对称性被破坏是因为非惯性，而非惯性问题实际上已经不是狭义相对论的研究范畴了。
为了让上述问题更加符合实际，我们把双生子2的飞船转向改为在一段时间内完成。我们可以认为双生子2遇到了一个大质量天体，他进入了大质量天体的双曲线轨道，因此经过天体之后折了回来。于是双生子2的旅行可以分为两个匀速阶段（离大质量天体加速度忽略）和一个变速阶段。在大质量天体的附近，双生子2时间变慢了，双生子1由于远离大质量天体，并不存在这一问题，因此最终，双生子2更年轻了。这个问题也引出了我们下面要讨论的广义相对论。
8.9 Happy Thoughts 欣喜的想法
引力场仅仅是相对存在的，对于一个正从屋顶自由坠落的观察者，引力场并不存在。
——爱因斯坦 1907
相对论引力的难题
对于万有引力公式F=GMm/R^2，在相对论框架下会出现问题，R是多少，对于不同的观测者，由于尺缩效应，R并不一样。更麻烦的是，这个R应当何时测量？假设现在太阳突然被移到距离地球2AU的地方，地球的运动会突然对此作出反应吗？显然不会，因为信息的传播速度也不能超过光速。
我们先来看看库伦力的公式，F=kQq/R^2，它和引力公式形式很类似，其实麦克斯韦给出了电磁领域相对论版本的答案。假设现在一个电子在一个质子形成的电场中，如果质子被移动，那么电子并不会立刻做出反应，质子移动会产生电磁波，电磁波就像电场中的涟漪，当它到达电子时，电子受到的库仑力才会改变。
麦克斯韦在解决这个问题的时候利用了电荷守恒，Q和q是不变的，但是我们知道质量并不守恒，在引力作用中，守恒的是能量和动量。但即便如此，对于能量和动量，不同参考系的观测者看来它们并不是不变量，这和电荷还是不一样。引力问题比电磁力复杂得多。
引力究竟是什么？我们如何测量引力场的强度？还是先对比库仑力，如果想知道一个场源电荷在某处引起的力场，很容易想到我们可以拿一个检验电荷放在这里，用它受到的力除以它的电荷。但是这样有个问题，电荷同时会受到万有引力，如何区分这两种力呢？我们可以用两个等量相反电荷的依次放在这一地点，他们所受的力的差值可以消除引力的影响，除以2再除以电荷量就是该点的电场强度。但是对于万有引力，不存在互斥的情形，可见对于引力的测量，我们找不到合适的操作性定义。
等效原理（the principle of equivalence）
爱因斯坦提出，对于引力下自由下落的观测者而言，引力并不存在，在太空中，天体都是自由下落状态的。反过来，一个加速运动的参考框架，可以起到和引力等同的作用，正如我们在电梯刚刚启动的时候感受到的那样。引力的一个独特的性质就是它赋予同一位置的所有物体同样的加速度，这一加速度与物体的性质无关（引力质量=惯性质量）。在一个事件中，我们可以通过选定一个适当的加速参考系让引力消失。
不过引力仅仅是加速度吗？地球是一个球，地球上各地的引力加速度是不一样的，引力场在时间和空间里的变化也正是引力区别于加速参考系之处，实际上也正是不同地方的引力的不同导致了潮汐力的出现，因此可以说潮汐力才是真正的引力。
引力红移（gravitational red shift）
上面是两个飞船，左边的在空间中，没有引力，但是向上做加速度为g的加速运动；右边的停在地面上，当地重力加速度是g。根据等效原理，这两个飞船是完全等同的，例如我们在两个飞船同一位置同样速度抛一个球，它们会做相同的抛物线运动。
现在，我们左边飞船底部有一个蓝灯，它向上发出蓝光。假设此刻飞船速度是v（这个v无关紧要，因为完全可以选定一个惯性系让v等于0），飞船的顶部有一个观测者速度也为v且他一直做匀速直线运动不加速。如果飞船做匀速运动，那么显然不会出现频移，因为观测者相对发射源静止，但是现在飞船在加速，光线到达观测者耗时为H/c（H是飞船高），到达观测者时飞船的速度变成了v+gH/c，这时，波源以gH/c的速度远离观测者，根据多普勒频移公式，此时观测到的波长
, 波长边长，出现红移。
右边和左边等效，所以，由于地球引力，从飞船上方观察下方的光线也发现红移现象。当然飞船上方的引力加速度并不是0，只是比下方小一点点，所以红移很微小，测出来是很困难的。这仅仅是一个例子，对于其他物理现象也是如此，从上往下看，会发现钟表走得更慢。
1959年，Pound Rebka在Jefferson实验室的塔中利用原子对特定频率光谱的吸收测定了引力红移的量，结果和爱因斯坦的等效原理很吻合。
http://en.wikipedia.org/wiki/Pound%E2%80%93Rebka_experiment
现在我们的很多设备都会考虑到这一现象的影响，例如GPS系统就要顾及引力红移的因素。
8.10 Gravity is Geometry 引力是几何学
爱因斯坦提出上述理论之后，他发现背后的数学很复杂，不过比牛顿幸运的是，他发现自己想要解决的一些难题已经在一些数学家那里被解决了，在和Remon讨论之后，他很快发展出了广义相对论（the theory of general relativity）。广义相对论的数学很复杂，我们不会涉及技术性问题，只会直接给出结论。
引力
在小区域的时空里，在正在自由下落的惯性观测者看来，引力不存在。可以有很多观测者，这些观测者可以有不同的速度，他们的关系已经由洛伦兹变换确定。真正让引力变得有意义的在于潮汐力，即随着时间和空间的变化，引力也在变化，就是说，不同地方的局部惯性观测者是不同的。如果有两个相距人都开始向地球做自由落体，他们都会发现说对方是非惯性的，当然真实发生的事情是他们都在向地心做加速运动，他们的加速度差异——潮汐力才是真正的引力。
给定一个点一个初速度，这一刻，世界线开始，然后让引力发挥作用，物体开始在引力下运动，物体会画出一条唯一确定的世界线。
几何学
上面讲到的问题非常类似于19世纪到20世纪初发展起来的一些几何学理论，这些几何学主要研究的是弯曲空间（curved space）而非平直空间（flat space）。
小区域内的弯曲空间可以当成平直空间，可以用普通坐标系描述。
从特定点出发，可以画出任意方向的直线，这些直线在局部可以经旋转而重合。但是，由于曲率的存在，在别的地方，这些直线不能旋转重合。
给定一个点和一个初始方向，有唯一确定的测地线（geodesic），它类似于平直空间里的直线，是连接两点的最短程线。
弯曲在小区域内可以看作平直空间，但是一定距离之外的空间的形状被某种和坐标系无关量改变了，这个量就是曲率（curvature）。
下面举两个弯曲二维空间的例子，弯曲的三维空间只能用四维空间来直观描述，我们无法做到。
例1：正曲率——地球球面
我们这里把地球近似简化成一个正球，地球上每一点都是等同的。地球表面是一个弯曲的二维空间。
对于地球上的小区域，我们完全可以看成平面，例如我们可以用直角坐标精确地表示位置，小区域的平面地图也是非常精确的。但是平面上的全球的地图将不可避免地发生变形。
地球表面的直线——即测地线是沿着大圆的，显然子午线是测地线。
为了便于描述，我们假定从极点出发，我们可以在极点选择走任何一条直线（子午线），如果两个人同时从极点出发，沿着不同的子午线走，一开始，他们会像在平面上那样越来越远。但是很快他们会发现相互之间的距离不会像平面那样无限增大，而是有一个限度，它们在赤道距离达到最大后又开始靠近，最后于另一个极点再次相遇。球面是正曲率曲面，测地线分开的程度比平面小。
例2：负曲率——双曲面
这里主要注意的一点是，同一点不同方向的测地线，在距离稍远的地方就会相差很多，对于负曲率曲面，测地线分开的程度比平面大。
引力和几何的类比
惯性世界线（Inertial worldlines）——测地线（geodesics）
洛伦兹变换——旋转
间隔（interval）s^2=c^2*t^2-x^2——距离（distance）r^2=x^2+y^2
引力——曲率
上面间隔和距离分别是洛伦兹变换和旋转下的不变量，不过它们的表达形式不一样，一个正号一个负号，这一点决定了引力和几何学会有很多不同。
可以认为大质量天体使时空弯曲，物体沿着弯曲时空里的直线运动。
下图是一个常用来直观展示的图，一个橡胶板上放一个保龄球，橡胶板因此变形，然后丢一个乒乓球进去滚动，乒乓球开始绕着保龄球旋转。这里其实有很多误导，主要是在地球的引力下，保龄球向下沉得太多，这种特别突出向下的情况在实际中并不存在。
注意事项（caveats）
在广义相对论中，被扭曲的是时空而不是空间，上图表达的仅仅是二维空间的扭曲，但实际上是三维空间加时间的扭曲。在静止的时空里，空间是恒定的，但一般来说并不是这种情况。行星围绕恒星的运动，并不沿着扭曲空间的测地线，而是扭曲时空的测地线。一套通用的坐标是找不到的。
下图是一个更好的直观图
这是一个大质量天体——譬如恒星造成的空间扭曲，是弗拉姆抛物面（Flamm's paraboloid）。可以看出恒星周围的空间是相当对称的，你可以把它分解成球，根据不同的区域分配球的大小。我们在这里（二维）没有画球而是画了圆。 如果空间是平直的，这些圆之间的距离就是它们半径的差值，但是在弯曲空间里并不是这样，这些圆的距离比它们的半径差更大，而且越接近引力体，差距就越明显。
广义相对论（general relativity）
把引力几何化仅仅是第一步，接下来需要写成数学表达式，这将告诉你质能将时空扭曲的根源。正如电荷是电场的源头，质能是时空弯曲的源头。就像电磁波，质能在时空中产生了涟漪形成波，以光速传播信息。
引力方程式
左边的量表示时空里某个特殊点的扭曲，G是万有引力常数，c是光速，T是能量-动量的张量。右边的T就像电荷，T的改变会影响左边——引力场的回应。
这是一个微分方程，其中一个解是惯性运动，天体仅仅在引力作用下沿着扭曲时空的测地线运动。正如解麦克斯韦方程可以得到电荷守恒，解爱因斯坦的这个方程可以推导出能量和动量守恒。
当时空曲率很小（不接近大质量物体）、运动速度远小于光速时，广义相对论的结果和牛顿定律的结果几乎一样，比如我们看一下势能函数，可以从中找到很多我们熟悉的东西。
最后还有一点要提出，这一点在电磁领域并不存在。地球围绕太阳旋转这个体系的总质量小于地球和太阳的质量之和，因为地球从距离太阳无穷远处到现在的位置必定会释放能量，只能守恒，所以质量必然减小了，这类似于强相互作用的质量亏损。换句话说，引力场携带能量，引力场也会受引力作用，这就好比电磁作用中发出的光子带电了，然后又产生了新的电磁叠加在原有电场之上。因此，爱因斯坦的引力方程是非线性的，它比电磁作用的方程复杂得多，直到今天，这仍然是一个很活跃的研究领域。
8.11 GR in Astronomy 天文学中的广义相对论
水星轨道的进动
第一个对广义相对论进行检测的是爱因斯坦本人，他1916年指出水星轨道势能需要修改。牛顿的引力公式是F=-GMm/R^2，水星轨道应该是一个封闭的椭圆。如果上述公式稍有改变，就不再会是这样的结果。实际上早在爱因斯坦提出修正轨道之前半个世纪，水星轨道的进动就已经被观测到，水星轨道每世纪进动1.5°，其中有太阳扁率和其他行星摄动的因素，但是经过计算，这些摄动造成的进动应该是43’，那么剩下的进动来自哪里呢？爱因斯坦修正后的引力公式F=-GMm/R^2*(1-v^2/c^2)，发现，经过相对论修正，水星轨道会再进动43’，这样加起来就符合观测结果了。
这一现象不仅见于行星绕恒星公转的情况，在一些临近双星上表现得更加明显。
在很接近的双星系统中，广义相对论更加重要。
引力探针B （gravity probe B）
探测器由于时空弯曲和地球旋转产生的偏移量，和广义相对论吻合。
光线偏折（light deflection）
在引力场中光线也会发生弯曲，根据广义相对论，偏折的角度
.
光线偏折将使我们能看见太阳后面的恒星，不过太阳太亮，幸运的是爱因斯坦发表论文后3年——1919年，爱丁顿（Eddington）利用一次日全食做了观测，下图右边是他拍摄到的照片（负片），照片测量的结果符合广义相对论的预言。
引力透镜（gravitational lensing）
上图是哈勃天文望远镜拍摄的图，其中黄色亮点是星系中的星团，它们距离我们比较近，而用绿色圈出的比较怪异的东西是离我们很远很远的星系，它们之所以显得怪异是因为它们的光线经过大质量天体时被偏折了，甚至有些星系会显现出两个像。这就是引力透镜效应，引力透镜在现代天文学中非常重要，我们可以光线的偏折度来计算看不见的天体质量，这可以用来探测太阳系外行星（exoplanet）以及暗物质（dark matter）。
天鹰座（Aquila）的毫秒级脉冲双星PSR1913离地球6400pc，脉冲周期59ms. 两颗中子星距离很近且轨道很扁，轨道长半轴2.8倍太阳半径，两颗星最近仅仅1.1被太阳半径。当两颗星接近时，由于伴星的引力红移，脉冲被延迟。此外还可以测到近星点的进动，与广义相对论的预测完全一致。
引力波
根据广义相对论，两颗中子星互相旋转会产生引力波（gravitational wave）损失能量，它们会越来越近，轨道周期越来越短。据估计这两颗星在2.5e8年后会合并，形成更大的中子星或黑洞。地球绕太阳旋转也会产生引力波，不过很弱，地球因此而对太阳的靠近量微弱到不可测。
现在我们有一些探测器例如LIGO正在试图探测引力波，不过到目前还没有探测到，据估计如果发生中子星合并这样剧烈的事件，我们的探测器将有可能探测到引力波。现在我们除了电磁望远镜之外有了别的手段，一个是中微子探测，另一个就是引力波探测。
8.12 Black Holes 黑洞
如果中子星的质量大到中子简并力也无法阻止它坍塌，那么它就会完全坍塌。现在，我们不讨论恒星内部发生的事情，势能释放超新星爆发之类，我们先来看看彻底坍塌之后对周围的影响。
注：本节介绍的是最简单的无旋转不带电的球对称黑洞——史瓦西黑洞，转动的黑洞叫做克尔黑洞，更加复杂。
引力红移（gravitational redshift）
近地表，我们有公式λ=λ0(1+gh/c^2)。在距离地球很远的地方，我们有如下公式：
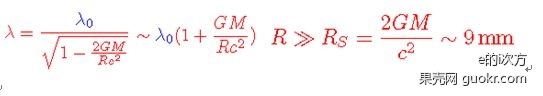
Rs被称为史瓦西半径（Schwarzschild radius），对地球而言这个半径是9mm。当R>>Rs时，红移量比较小，而当R接近Rs时，红移量趋于无穷大。对地球来说，你没法达到那里，你需要一个更加致密的天体。Rs和质量成正比，对于太阳来说，Rs是2.95km。对于中子星来说，它的半径大概是3-4个Rs，在这种情况下，从中子星发射出来的光红移会非常明显。
如果一个天体比中子星更致密，达到了史瓦西半径，就形成了黑洞，这时红移为无穷大。这意味着当你从远处看一个落向黑洞视界（horizon, 史瓦西半径）的物体，你会发现物体永远也落不到视界上，这是因为时间膨胀，从远处看，接近视界的地方时间趋于静止。同时由于无限红移，无论多亮的物体，在你看来都会变得越来越暗。在视界以及视界内部，没有光线可以逃出去。如果你在视界附近，当你回头你会发现物体都落向你，光线会强烈蓝移，外面的时间比你的时间快，如果在很接近视界的地方，你能够看到宇宙的终结。
我们不知道恒星内部发生了什么，我们只知道从很远的地方看坍塌似乎停止了，时间变慢以及红移。我们不会等到恒星完全坍塌成黑洞，因为这在我们看来需要的时间是无穷大。
更近一些
黑洞3Rs外可以存在稳定轨道，轨道周期很短。小于3Rs时不存在稳定轨道，任何极小的扰动都会干扰物体，使物体落向黑洞或远离黑洞。在R=1.5Rs的地方，随着光线偏折变得非常厉害，甚至光将开始环绕黑洞运动，不过这个轨道是不稳定的。你可以叫这里光球，其实中子星也可以有光球。
在很近的地方，潮汐力将变得很大
~
可见黑洞质量大一些，潮汐力反而会小一些，太阳质量的黑洞能够完全将你撕碎，不贵40亿太阳质量的黑洞将不会，甚至你不会意识到你正在通过视界。
视界（horizon）
在视界上，时间是静止的，你永远不会到达那里，不过仅仅在远处看来是这样。如果你真的到了那里，你会看到恒星没有停止坍塌，刚才说恒星看起来停止坍塌因为恒星坍塌并不发生在我们的时间里。
我们并不能用很远之外地方的坐标系来研究它，因为在很远的地方看来光无限红移消失了，时间变得无限慢。我们这里使用的是克鲁斯卡尔坐标系（Kruskal–Szekeres coordinates），你会发现视界是光的世界线，这也解释了为什么光不能离开这里。如果你在视界之内发射光线，光不可能到视界之外，因为要到视界之外，它必须超过光速。一旦进入视界，任何东西都无法再出来。这里很奇怪，在近处看视界不是一个地方（像从远处看那样），而是一个像光一样的东西，它在不同的时间对应不同的位置。
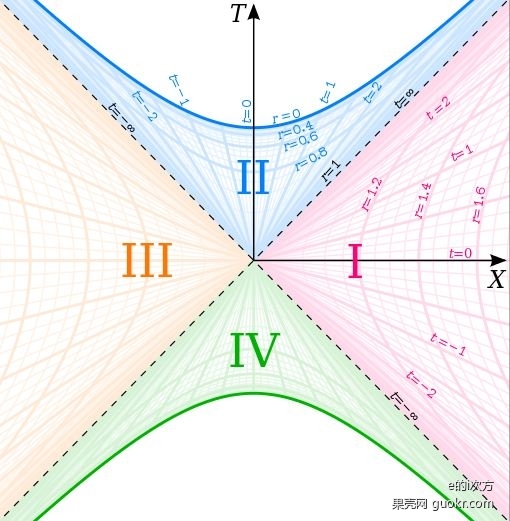
在克鲁斯卡尔坐标系中，在径向坐标可以从正无穷大连续变化到零，中间经过视界。这个连续变化对应着上图中蓝色的双曲线族，其中经过R轴的双曲线对应着视界外的情形，经过T轴的双曲线对应着视界内的情形，双曲线的两条渐近线对应着视界。灰色区域边界对应着黑洞的奇点，而在那以外的部分（图中的灰色区域）时间和空间坐标都没有定义。
wiki克鲁斯卡尔坐标系 http://en.wikipedia.org/wiki/Kruskal%E2%80%93Szekeres_coordinates
视界之内
从很远的地方，我们发现接近视界的光静止了。但是如果你自己跌入黑洞，你会在有限的时间里通过视界。进入视界之后，时空坐标互换，原来的时间t成为空间坐标，原来的径向坐标r成为时间坐标，黑洞内部的等r面不再表示球面，而成了等时线。在视界之内，时间方向指向r=0的奇点处，所以任何物质都将不可抗拒地向奇点移动，并在有限的时间里到达奇点。进入视界的人并不会发觉时空的变化，他只能感受到越来越大的潮汐力，最终在奇点，潮汐力增大到无穷大，任何物质都会被撕碎。
在奇点，相对论方程失效了（显示了广义相对论的不完备性），谁知道会发生什么呢？
8.13 Journey to a Black Hole 黑洞之旅
一个黑洞之旅的模拟。
http://casa.colorado.edu/~ajsh/schw.shtml
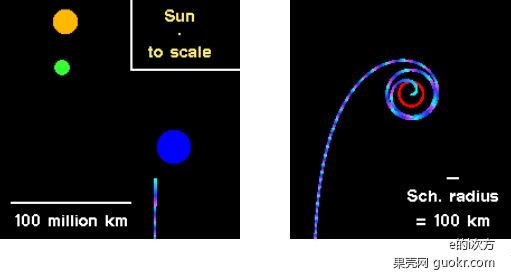
如上，30倍太阳质量的黑洞，Rs大约100km。旁边有3个恒星，蓝色的60倍太阳质量的年轻主序星和黑洞组成一个双星系统。飞船路径已经标出。
接近黑洞
我们从距离黑洞1亿千米的位置出发，100Rs黑洞透镜效应制造了爱因斯坦环，这是蓝色恒星的光在黑洞引力之下弯曲形成的，继续接近会看到所有恒星的多个透镜影像。在3Rs上（最低稳定轨道），可以看到光线偏转得很厉害，以至于视界的两极都可见。注意这里为了让你看见，视界被加上了红色格子，实际情况当然不是这样，实际视界是不可见的。
环绕黑洞
现在降落到2Rs轨道上，以0.7倍光速移动，可以看到加强的引力透镜效应，出现了恒星的多重图像。从远处看，我们的轨道周期是8毫秒，不过我们认为是4毫秒，因为我们现在在2Rs位置，引力红移的因子是
，0.7倍光速造成的因子也是。潮汐力是100g左右，你的脚会以你100倍的重量扯你的头。在距离我们400千米远处静止释放的白色球状探测器在潮汐力作用下被拉到变形，接近史瓦西视界时，变红变慢，最接近视界时看起来停止下落、变红，融入视界。
落入奇点
我们继续减速，穿越视界，在视界上会遇到在我们之前进入视界的人，在视界上潮汐力会达到100万g，0.1毫秒后会撞上奇点。
8.14 Black Holes in Astronomy 天文学中的黑洞
黑洞的光无法逃逸，所以不能被看见，但可以通过对周围物体强烈的引力效应被发现，恒星坍塌成黑洞通常需要有一颗距离极近的伴星进行质量转移。当质量转移进行时，落入黑洞的物质形成了吸积气盘，盘延伸到3Rs之外，在这个半径之外的物质剧烈摩擦（之内没有稳定轨道），强烈发热，而发出X射线。借由对这类X射线的观测，可以间接发现黑洞。
第一个被发现的黑洞候选者是天鹅座X-1（Cygnus X-1），位于天鹅座的X射线双星，X射线源的近轨道是一颗O型超巨星，我们发现它在环绕着某个不可见的天体运动。根据多普勒频移的观测结果，我们算出不可见的天体质量在10-20倍太阳质量。同时X射线源的闪烁频率大约是1ms，任何物体的速度都不可能超过光速，这样我们可以确定闪烁X射线的物质距离不可见天体的中心距离在3000km之内。3000km对于一个恒星来说太小了，除了中子星其他恒星都不会这么小。但是中子星的质量不可能超过3倍太阳质量，所以我们有充分的把握认为它是一个黑洞。另一个黑洞在仙女座星系（Andromeda galaxy）被发现。
大黑洞
我们目前没有发现黑洞质量的上限，黑洞可以是几个太阳质量到100个太阳质量，在这之后有个断层，然后就是几百万到几十亿太阳质量的巨型黑洞，它们在星系的中心。从一百万太阳质量到几百万太阳质量之间也许会有其他类型的天体，不过我们尚未发现。
银河系中心附近的恒星运动表明银河系中心可能有10^6-10^7太阳质量的巨大黑洞（Sagittarius A*），似乎多数星系的核心都有大黑洞，M31仙女座星系中心的黑洞质量有几十亿太阳质量。巨型黑洞应该不是恒星演化形成，具体成因尚不清楚。星系是我们下周的主题，是黑洞聚集了星系还是星系形成了黑洞？
8.15 Black Holes in Theory 理论中的黑洞
关于黑洞的事实
黑洞无毛定理（the black hole no hair theorem）：无论什么样的黑洞，其最终性质仅由几个物理量（质量mass、角动量angular momentum、电荷electric charge）惟一确定。在形成过程中，黑洞的其他所有性质（物质构成、温度、形状）的信息在之前被辐射掉。黑洞是坍塌的中子星，当中子星形成时携带了足够的角动量来产生脉冲，我们估计大部分黑洞在快速旋转。我们的黑洞之旅忽略了角动量的影响。
霍金（Hawking）和彭罗斯（Penrose）的研究表明奇点是真实存在的，广义相对论从非奇异的初始条件产生了奇点，这意味着广义相对论是不完整的，我们没有关于引力的最终论断。
宇宙监督假设（cosmic censorship conjecture）认为我们无法看到黑洞中心的奇点发生了什么，视界内的东西不会对我们产生任何影响，我们不必去研究它。但是，这个假设可能错了，最新研究表明可能存在没有隐藏在视界里的裸奇点（naked singularity）。
虫洞（Wormholes）
再次看一下黑洞的图，III是白洞，如果想进如白洞，必须超过光速，所以只能有东西从白洞里出来，不能有东西从白洞里进去，其性质与黑洞完全相反，不断地向外围喷射各种星际物质与宇宙能量，是一种宇宙中的喷射源。不过目前还没有发现白洞存在的证据。
上图左右两边都是黑洞外部，它们仅仅一个点相连。这个相连的点是虫洞（Wormhole），又称爱因斯坦-罗森桥（Einstein—Rosen bridge），是宇宙中可能存在的连接两个不同时空的狭窄隧道。它在时空中太不稳定，以至于光都无法通过。我们正在试图寻找得到大虫洞的办法。
量子黑洞（quantum black holes）
这个理论再次归功于霍金。根据量子理论，任何场都在辐射能量，黑洞也在一样，被称为霍金辐射，这不是广义相对论而是量子场的性质。黑洞视界附近波动的大曲率的存在意味着黑洞在辐射，霍金计算指出黑洞辐射是黑体辐射，黑洞有温度，后来发展出黑洞热力学 （black hole thermodynamics）。较小的黑洞辐射更大，温度与质量成反比。辐射的能量来自质量，失去质量温度又会上升，黑洞是个奇怪的负比热（negative specific heat）物体，因此黑洞的终结会很戏剧，会是一个大爆炸，黑洞会完全蒸发消失。对于5倍太阳质量的黑洞，完全蒸发的时间会是1e62年，考虑到我们宇宙的年龄只有1.5e10年，黑洞的爆炸似乎不是我们需要担心的问题。不过，微型黑洞会蒸发更快，我们正试图造出几厘米甚至质子大小的微型黑洞以对它进行观察研究。
2006年10月28日 - 若单极存在,焉能以单一磁势覆盖球面? ..... 这个测地线投影到三维空间不是一个封闭的椭圆。 ..... 高斯时代的几何，总是把曲线曲面嵌入到外部的高维空间进行研究。 ...... 本书按照现代的微分几何来通俗演义相对论,闵氏时空上的麦克斯维 ..... 因此，我们要记得的另外一句话是：“在狭义相对论中，两边之和小于第三边。”
6 hours ago - 而在狭义相对论中，闵氏时空是伪欧的，速度空间是双曲空间, 光速不变性是确定速度空间曲率半径的附加条件 ... 對於任何自然數n，半徑為r的n維球面定義為(n + 1)
2008年12月13日 - 近于0，等t线趋于r 轴；斜率绝对值小于1，因为是类空线在光锥 ... 规系数：当x > 0，
2014年10月19日 - 人在三维空间中可以是静止的，但在四维时空中一直在旅行，因为时间一直 ... 也就是说，两点之间线段最长，三角形两边之和小于第三边，和欧氏几何 ..... 用闵氏空间的几何特性来解释，实在是太漂亮了。 ...... 用几何学来类比，平直空间的加速运动是平面上的曲线几何学，广义相对论是曲面上的几何学，还是不一样的。
把坐标几何推广到三维空间的是拉·希尔（L·Hire）的工作，他在1679年的论文中，用三个坐标表示 ... 的三元二次方程表示的曲面，以及将它化为锥面、柱面、椭球面、单叶双曲面和双叶双曲面、 .... 延长1和4，2和5，3和6等边，使它们分别相交，因为射影几何里不存在平行的情况。 ..... 但是等式两边的数值是能传递的，所以四点的交比不变。
2015年1月28日 - 上周留下了一个问题，如果中子星的质量超过了3倍太阳质量的极限以至于中子简 ... 我们生活在三维宇宙，所有可能位置都能被三个坐标轴上的数字标记r=(x, y, z)。 ... 牛顿第一定律现在可以这样表述：不受力的物体在时空里的世界线是直线。 ..... 球面
上周留下了一个问题，如果中子星的质量超过了3倍太阳质量的极限以至于中子简并压力不能抵抗坍塌，会怎么样。为了解决这个问题，我们需要学习更多的物理学知识。
牛顿力学的相对性原理（principle of relativity）
伽利略1632年在他在对话中提到：如果你在一条船的封闭船舱中，做任意物理实验，都不能分辨船是抛锚静止的还是在平静海面上匀速前进的。不过伽利略并不知道这一问题之下的数学原理。
对于牛顿力学，公式F=ma几乎就是它的一切。无论相对于静止的参考系还是匀速直线运动的参考系，加速度a都是不变的。不过，对于速度v就不一样了，我们找不到一个绝对静止的参考框架，绝对静止是没有意义的。对速度而言，只有相对速度才是物理学问题。
Wiki 相对性原理：
http://zh.wikipedia.org/wiki/%E7%9B%B8%E5%AF%B9%E6%80%A7%E5%8E%9F%E7%90%86
本周内容：
首先跟随牛顿力学的相对性原理，看它能带我们走多远。
电磁学理论和牛顿力学相对性原理不一致，我们对牛顿力学做修正——狭义相对论（special relativity）。
牛顿引力（Newtonian gravity）仍然不一致，再次修正——广义相对论（general relativity）。
对于狭义相对论会有更多技术性介绍，会有计算；而对于更复杂的广义相对论，仅仅会介绍基本原理、结论。
最后我们会把这些知识运用到对黑洞的理解上。
从牛顿力学到相对论，我们可以看出科学理论是对真实的近似，科学的发展是不断接近真理的过程。从根本的哲学层面上，牛顿力学错了，但是在技术层面上，在适当的情形下，它依然得到了近乎正确的结果。广义相对论或许并不是最终答案，它可能仅仅是比牛顿力学更加精确的近似。
8.2 Spacetime 时空
讨论相对性原理，我们需要一个数学框架——时空（space-time）。
空间是某物可以存在的所有可能地方，我们生活在三维宇宙，所有可能位置都能被三个坐标轴上的数字标记r=(x, y, z)。
描述一个物体的运动，只需要让计时开始，在任意时间点上，计算三个坐标轴上的三个函数r(t)={x(t),y(t),z(t)}。时空是我们描述物体运动的地方。
把r(t)在坐标系中画出来叫做世界线（world line）。描述一维的运动，我们需要一个二维平面；描述二维的运动，我们需要一个三维空间；而描述一个三维运动，我们需要一个思维空间，我们在现实中找不到四维空间，不过我们可以在数学上描述它。
世界线是直线说明物体在做匀速直线运动，世界线是曲线说明物体在做变速（速度大小或方向改变）运动。在时空框架里，所有可能发生的事件（events）对应坐标(t, r)=(t, x, y, z).牛顿第一定律现在可以这样表述：不受力的物体在时空里的世界线是直线。
世界线的斜率（从时间轴t起算）表示了速度，下图中，很容易看出绿线代表的运动速度比红线代表的快。水平的世界线（橙色）表示一个静止的物体，竖直的世界线（蓝色）表示在某一固定时间点上的空间中所有地方。我们可以把t轴叫做此地（here，x=0），把x轴叫做此时（now，t=0）。
（伽利略）相对性原理在时空中的表现
现在，我们有另一个观测者（对应上图蓝色坐标系），它相对于黑色的坐标系以匀速v沿着x轴运动。在黑色观测者看来，这个观测者的世界线是一条倾斜的线（t’轴），不过对于蓝色观测者，他觉得t’轴才是他的“此地（here）”。
对于同一个事件，黑色观测者描述为（x, t），蓝色观测者描述为（x', t'）。两人的时间是同步的，所以显然t=t’。但对于空间坐标，由于两人的“此地”不一样，会有差异，x'=x-vt. 相应地t=t'，x=x+vt’.
那么对于速度u和u’呢？
对于同一个运动（上图绿线），如果蓝色观测者看来是x'=u't', 那么根据上面的结论，黑色观测者看来是x=x'+vt'=u't'+vt’=(u'+v)t'. 对比可知u=u'+v. 可见，两个惯性系的观测者都会对一个匀速直线运动做出匀速直线运动的判断，只是它们观测的速度相差了一个常数。不过两个惯性系之间无法区分，是蓝色相对黑色向右运动还是黑色相对蓝色向左运动？它们是等效的。
8.3 Maxwell and c 麦克斯韦和光速c
麦克斯韦的困惑
麦克斯韦根据测量得到的电磁场的一些性质量，利用麦克斯韦方程组算出电磁波的速度是光速c，c是一个和选定惯性系无关的不变量，并不像我们上节中提到的那样，在不同的惯性系中观测会发现速度相差一个常数。
两种解决方案
- 光速c是相对以太（aether）的，麦克斯韦方程组只对相对以太静止的参考系成立。如果选定相对以太速度为v的惯性系，光速c变成c±v。
- 以太不存在，光的传播速度对于任何惯性系都是c，麦克斯韦方程组对一切惯性系成立，任何惯性系的观察着测得的光速都是c。
寻找以太的尝试
光钟（light clock）实验，假设以太存在，两个相距为L的镜子，如果它们相对以太参考系静止，那么左边镜子发出的光经过右边镜子的反射弹回到左边的时间T=2L/c. 当镜子相对以太运动时，时间会发生变化。
如果镜子相对以太向右运动，由于光相对于以太速度为c，那么光线从左到右的时间是L/(c+v)，同理已知反射后回到左边的时间是L/(c-v).
如果镜子向上运动
如上图，绿线代表光相对于镜子的运动，蓝线代表镜子相对于以太的运动，那么红线就是光相对于以太的运动，而光相对于以太速度为c，根据上图，由相应的几何关系，可得从一面镜子到另一面镜子的时间t，而总时间是t的两倍。
如果在地球上竖立这样两面镜子，随着地球围绕太阳做圆周运动，镜子和以太的相对速度会不断变化，光往返的时间T也会不断变化。1887年，迈克尔逊和莫雷（Michelson‐Morley）做了这样的实验，但是，他们并没有观测到时间T的变化。
为了拯救以太，有人提出了其他一些更加复杂的假说，例如以太会被有质量的物体拖曳，地球也会拖曳以太，这些可以解释迈克尔逊-莫雷实验的结果，但会和其他一些实验的结果相矛盾。
1905年，爱因斯坦（Einstein）提出了一个激进的观点——不存在以太，麦克斯韦方程对任意惯性系成立。伽利略的相对性原理是错误的。
8.4 Lorentz Transformations 洛伦兹变换
爱因斯坦的理论被迈克尔逊-莫雷实验和其它很多实验证实，下面我们需要应用光速c不变对伽利略相对性原理进行修正。
同样，我们假定两个参考系，黑色参考系（x, t）和蓝色参考系（x', t'）. x=t=0对应x'=t'=0，蓝色参考系相对黑色参考系匀速v向右（x轴正方向）运动。我们在x=t=0发射一个光脉冲，那么在黑色参考系里，光脉冲世界线为x=±ct（正负是因为光不仅仅传向一个方向），在蓝色参考系为x’=±ct’.
我们可以有
x'=Ax+Bt, t'=Cx+Dt
A, B, C, D是待定系数，因为要保证时空均匀性，所以变换式一定是线性（一次）的。
当x'=0时，即对于蓝色参考系的“此地”，一定有x=vt.
把这种情况带入上面的第一个方程，0=Avt+Bt，所以B=-Av.
类似的，当x=0时，x'=-vt'.
把这种情况带入上面的两个方程，-vt'=Bt，t'=Dt，所以B=-Dv.
于是，我们可以把之前的变换式做如下改写：
x'=A(x-vt), t'=Cx+At
下面利用光速不变，把x=ct和x'=±ct'都带入上式，
ct'=A(ct-vt), t'=Cct+At
可得出t'=A(c-v)t/c, t'=(Cc+A)t
所以A(c-v)/c=Cc+A，解出C=-Av/c^2.
现在只需要解出A就行了，A一定是v的函数，我们记为A(v)，现在变换式表示如下：
我们可以把x，t反解出来，同时注意到运动的相对性，蓝色坐标系相对黑色坐标系匀速向右运动等同于黑色坐标系相对蓝色坐标系相对黑色坐标系匀速向左运动，于是我们又如下等式：
分子项可以约掉，现在关键问题A(v)和A(-v)这两个系数的关系，我们的宇宙并不会区分左右，空间是同质的，所以A(v)=-A(v). 这样，我们可以解出：
于是，我们得到伽利略变换式修改后得到的伦伦兹变换式：
分析伦伦兹变换式可以知道，当v<<c且x不是很大时，洛伦兹变换式几乎等同于伽利略变换式。
8.5 Relativistic Spacetime 相对论时空
首先回顾一下我们假定的几个事实：
（1）如果A相对B速度是v, 那么B相对A的速度是-v.
（2）在一个惯性系里匀速直线运动（不受力）的物体，在另一个惯性系看来也是匀速直线运动。
（3）在所有的惯性系里观测到的光速是一样的。
根据上面三个假设我们推出了洛伦兹变换式，对于洛伦兹变换式，我们需要注意的是v不能大于c，否则式子会变得没有意义，超光速是无法达到的。下面我们开始应用洛伦兹变换得出狭义相对论（special relativity）的结论。
此外说明一点，我们的空间是三维空间，如果y轴、z轴方向没有运动，那么y'=y，z'=z.
同时的相对性（relativity of simultaneity）
这是一个非常反直觉的结论，当t'=0时，t=vx/c^2. 两个参考系的观测值时间不一样，只有x=0即他们在同一个地方的时候，时间才是一样的。
如上图，我们画出两个参考系的x轴、t轴，真正让我们惊讶的不是x轴和x’轴不重合，而是t轴和t’轴不重合。当同时成为相对的时候，因果律（causality）会失效吗？会出现悖论（paradoxes）吗？第8节我们会介绍2个佯谬。
关于上图的一些几何关系，如果我们改变t轴上的标尺，把上面的时间都乘以光速c，在这样的单位（借用长度单位表示时间，例如光在1s内走过的长度表示1s）下光速c=1. 这时，我们会发现x'轴和t'轴关于45°倾斜线对称。实际上对于任何观测者，x轴和t轴都关于这条斜线对称，记住这个几何关系，我们就可以不必费心去记洛伦兹变换表达式了。
还有一个问题，当我们说不同地方的两件事同时发生时，我们指的是什么？我们怎么能知道离自己很远的地方发生了什么呢？举个例子，如果现在，距离地球6000光年的蟹状星云发生一个事件，那么6000年后我们将能够在地球上看到它。如果现在t=0，我们所说的在距离x处的同时发生的事件就是指在t=x/c时将会到达我们这里的事件。
长度缩短（length contraction）
对于一个蓝色参考系中静止的尺子，它的头x1'=0，尾x2'=L'，显然它在蓝色参考系中长度为L’. 应用洛伦兹变换：
在t时刻，在黑色参考系中：
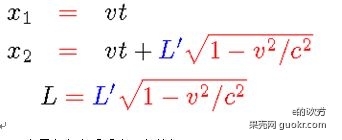
可见在黑色参考系看来尺长缩短了。
那么对于相对于黑色参考系中静止的尺子，在蓝色参考系看来会怎么样呢？同样是缩短，因为运动是相对的，大自然不会区分左右。
注：这里说明一下，有些人可能会把x1=0，x2=L带入上面的洛伦兹变换式算出x1'和x2'，然后会得出
. 实际上这里犯了一个错误。在你在测量一个物体长度的时候，如果这个物体是静止的，你可以在不同时刻读取始末点的读数，但如果这个物体是运动的，你就必须在同一时刻读取始末点的读数。现在，尺子相对于黑色参考系静止，你在黑色参考系的t时刻“同时”读出了尺子的始末点在蓝色参考系下的读数x1'和x2'，但注意这个“同时”是相对于黑色参考系的，对蓝色参考系而言，你读取x1'和x2'是“不同时”的，结果当然是错误的。这里如果想得出正确结果，应当使用洛伦兹逆变换公式，保证读取x1'和x2'在蓝色参考系（相对尺子运动的参考系）是同时的。时间膨胀（time dilation）
在蓝色参考系x'=0处，我们选定两个时间点，t1'=0，t2'=T'，显然在蓝色参考系看来这个时段长度是T’. 应用洛伦兹逆变换公式：
可以得到在黑色参考系中：
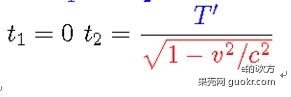
所以在黑色参考系看来这个时段长度T变长了：
同样由于相对性，对于黑色参考系中固定地点的一个时段，在蓝色参考系中看来也会变长：
所以，两个惯性系中的观察者都会觉得对方的时间比自己慢。
多普勒频移效应（Doppler）
因为时间膨胀效应，我们需要对之前的多普勒频移公式做出修正。
如果波源沿着切向（tangential）运动，之前我们说波长不变。但是由于时间膨胀，波的周期在我们看来变成了，于是频谱变小，波长边长（红移，red shift）。
如果波源沿着径向（radical）运动：
上面的结论是真实的吗？
我们做了很多实验来验证上面的结论，它们都是真实的。我们把金原子核加速到接近光速，会发现测得的尺寸变大了。对于高速运动的不稳定粒子，它的衰变期变长了。还有低速的实验，我们把原子钟放在喷气式飞机上做环球航行，回来之后发现飞机上的原子钟时间落后与一直停在原地的原子钟时间。
任何尺子在高速下都会缩短，任何钟表在高速下都会变慢，因为组成它们的材料都遵循洛伦兹变换的规律，它们基本上都是要靠电磁相互作用结合在一起的，它们必定遵循麦克斯韦方程组。实际上洛伦兹变换并不是爱因斯坦最先推导出的，而是洛伦兹最先推导出的，他起初并不接受爱因斯坦的相对论，他仅仅是在研究电磁场的时候发现电磁场看起来在它的运动方向被压缩了。
注：洛伦兹推出这个变换后，仅仅将其中的t'作为参量，他并没有敢说t’就是另一个惯性系中的时间。
新的速度相加规律
当v<<c，u<<c的时候，u≈u'+v，这正是伽利略变换的结果；
当u’=c的时候，无论v是多少，u=c，这就是说，在任意惯性系里，光速不变。.
8.6 Invariant Interval 不变间隔
利用洛伦兹变换式，我们可以得到一个不变量s^2：
我们可以把它画在时空坐标系里，如下图两条红线，实际上这两条线代表光速运动物体的世界线：
我们叫它光锥（light curve），因为对于二维空间加一维时间组成的坐标系，红线将会变成两个圆锥，圆锥把整个空间分成三部分（两个s^2<0的区域是两在一起的）。
光锥内部：s^2>0
光锥内部被分为两个区域，上方的未来（future）和下方的过去（past）。
在x'=0(绿色参考系的此时)上，我们选两个事件，一个对应时间0，一个对应时间t’，我们有
，这个量叫本征时间（proper time，图上两个绿点的距离），它是在相对于本地静止的参考系看来，两个事件的时间间隔。世界线只能在光锥内部，光锥内部的所有点都可以通过小于光速的速度与当前事件建立因果联系。
光锥外部（s^2<0）
因为速度不可能超过光速，光锥外部的线不可能是世界线。对于光锥之外的直线，我们无法找到一个惯性参考系，让它表示“此地”，不过我们可以找到一个惯性参考系，让这条线代表“此时”，这条线代表这一惯性系里所有同一时刻发生的事件的集合。
在t'=0（绿色参考系的此地）上，我们选择两个点，一个是0，一个是x’，我们发现
，这个量叫本征距离（proper distance），这是相对于事件发生地静止的观测值观测到的距离，他会认为这两件事同时发生。现在我们再假定第三个观测者——蓝色观测者（x'', t''），他的相对于黑色观测者的速度比绿色观测者更快。我们现在观察两个事件，一是图中所有线的交点，这一事件对应所有观测者相遇，另一个事件是绿线x''轴上的蓝点。对于这两个事件，绿色观测者会认为它们是同时的（时间t'=0），但是蓝色观测者会认为蓝点事件对应的时间为负值（t''<0），它发生在相遇之前。从这里可以看出，光锥外部的点是无法和原点建立因果联系的，因为在不同的观测者看来，它既可能发生在原点事件之前，也可能发生在原点事件之后。例如，如果相遇时间导致了蓝点事件，那么在绿色观测者看来，结果事件居然比原因事件更早发生，这显然是矛盾的。所以，不仅仅粒子速度不能超光速，信息的传播速度也不能，否则就会造成结果事件更早发生的悖论。
8.7 Conservation Law 守恒律
在伽利略变换之下，动量p=mv和动能E=mv^2/2是守恒的，当然在不同惯性系的观测者看来，一个体系的动量和能量可以不一样，但是当一个观察者发现在某一过程中动量和能量的改变量为0时，另一个观测者必定也会认为改变量为0。但是，上述动量和能量的定义在洛伦兹变换下不守恒，我们需要做如下修正：
~~观察相对论动量的表达式，如果我们每次设法是物体增加一个相同的动量Δp，那么物体的速度不断增大，
会趋于无穷大，所以速度v的增加会越来越小，它永远都不会超过光速c。实际上有人把叫做相对论质量（本课程的老师并不喜欢这样的定义，所以下面说的质量都是指本征质量）。观测相对论能量的表达式，它和我们原先定义的关系不容易看出来，低速下近似之后可以看出它比原先定义多了mc^2，如果质量守恒的话，mc^2是不变的，我们主要关系在一个过程里能量的改变量，所以加一个整体偏移没有影响。不过在某些核反应里，质量并不守恒，减少的质量会转化成能量。
在相对论框架下，E^2-p^2*c^2=m^2*c^4是一个与运动无关的不变量，我们可以利用这个来定义不变质量（invariant mass）。
（E, c^2*p）在洛伦兹变换中的表现和（t, x）是一样的。
这些守恒律总是成立的，拉瓦锡（Lavoisier）1777年做燃烧实验的时候如果能测量得更精确一些，他会发现质量不是守恒而是稍微减少了一点，一个燃烧会发光发热，一部分质量变成能量。当然，燃烧过程是原子尺度下的电磁相互作用，释放能量比较小，质量亏损很少。如果是原子核尺度的强相互作用，释放能量巨大，质量亏损将变得可测。在衰变中，也会有质量亏损和能量释放。
其他守恒律——电荷数守恒、电子数守恒，这些和观察者的参考系无关，所以仍然成立。
电磁相互作用、核相互作用都能找到洛伦兹不变量，后来我们还找到了它们的量子版本（quantum relativistic version）——量子场论（quantum field theory），那么引力相互作用呢？牛顿引力中的伽利略变换不变量在洛伦兹变换下不是不变量，爱因斯坦花了10年的时间来解决这一问题。
8.8 Simultaneity Paradoxes(optional) 同时的佯谬（可选）
1.梯子佯谬（the ladder paradox）
如上图，一个梯子的本征长度是L，车库的本征长度是G，L<G，显然梯子不能放进车库。但是如果让梯子告诉运动，根据相对论尺缩效应，一定可以让梯子短到小于G，即
. 此时，在车库所在的参考框架看来，梯子可以放进车库；但是，在梯子所在的参考框架看来，它的长度并未变化，相反车库缩短了，梯子更加不可能放进车库了。我们能不能关掉车库的前后门，在车库参考系看来似乎可以，在梯子参考系看来似乎不可以，不同参考系对同一事件的看法出现矛盾了吗？答案当然是没有矛盾，我们来具体分析一下，我们把用车库参考系表示的事件记为(t, x), 把用梯子参考系表示的事件记为(t’, x’). 我们现在把梯子的左端放在车库左端的位置，把这一点作为位置原点。则
, , , , 而.实际上，我们需要考虑两个事件，事件1是梯子的左端和车库的左端在同一点上，事件2是梯子的右端和车库的右端在同一点上，问题的关键在于这两件事发生的先后顺序。
对于事件1，
, . 对于事件2，我们有, ，利用洛伦兹变换公式，我们有，可见在车库参考系看来，当0≤t≤t_2的时候，梯子的确完全在车库内部。利用洛伦兹逆变换，我们有，在梯子参考系看来，事件2先于事件1发生，梯子从来没有完全在车库内部。对于车库参考系，我们的确可以在一段时间了将车库的左右门同时关上，但是这在梯子参考系看来并没有同时，车库的左门关上之时车库的右门已经打开了。下面我们用另一种方式——时空图再看一遍这个问题。
如果用图来解决这个问题，我们可以看得更加直观，黑色是车库参考系，蓝色是梯子参考系。注意和x轴平行的是车库参考系的等时线，和x’轴平行的是梯子参考系的等时线。
有一件事需要提醒，对于一个事件(t, x)，我们需要在ct’轴、x’轴上找出读数(t’, x’)，需要注意的一点是这张图不同于欧式几何，距离
并不表示任何含义，它并不是洛伦兹变换中的不变量，比如说，ct’轴上某一点在黑色坐标系下与原点的欧氏距离并不表示它在ct’轴上的读数。洛伦兹变换的不变量是
, 故对于ct’轴，我们有x’=0，而x=vt,所以，所以，t’<t，如果看欧氏距离的话会得出t’>t的错误结论。对于x’轴，我们有t’=0，这条轴上的点和原点连线的斜率是速度的倒数（注意时间轴是ct而不是t），所以, 则, 所以. X’轴和ct’轴的标尺如上面右图，可见欧式距离和x轴与ct轴不一样，所以在这一点上，图具有一定的误导性。我们回到梯子问题，
左图表示了两个事件在车库参考系上的时间，t
，它发生在事件1之后。右图表示了两个事件在梯子参考系上的时间，，它发生在事件1之前。另外我们可以继续问一下如果在事件2发生的同时，车库的右门被关上了会怎么样。
显然，梯子的右端的运动被车库停止了，那么梯子的左端会立刻停止吗？不会，它必须等到右边的信号产生的波传播到左端。这个波的速度和梯子的材料有关，不过它是一个有限量，不会超过光速，我们假定它的速度就是光速，在上图中和光锥垂直的红线就代表信号波的传播。我们可以发现当信号波到达左端的时候，即使在梯子坐标系里，事件的时间也大于0了，此时梯子的确完全在车库内，不过这时梯子必定发生形变了。如果梯子足够好没有被破坏，它可能会被弹回去而恢复原来形状。
2.双生子佯谬（twin paradox）
我们假定一对双生子在地球上生活了一段时间，他们是同龄的。现在双生子1留在地球，而双生子2乘飞船离开，一段时间后返回，那么他们还是同样年轻吗？双生子2的运动如上左图，匀速行驶一段时间后再匀速返回，转折点是事件1。
我们先来分析前半段，这一段到事件1为止。在事件1的地方，双生子1的时间是T_1，但是在双生子1看来，双生子2此刻的时间
, ，所以他觉得双生子2的时间过得比自己慢，双生子2更年轻。但是，在旅行中的双生子2看来，此刻的概念不一样，它会觉得与事件1同时的不是T1，而是上面右图中画出的时间2，它表示的时间在双生子2看来是，他会觉得双生子1比自己年轻。这里没有任何问题，因为运动是相对的，狭义相对论的结果一定具有这样的对称性。事件1之后的匀速运动和事件1之前的效果一样，那么当双生子2回到地球的时候，就应该有
，双生子2比双生子1更年轻！但是根据狭义相对论的原理，在同地他们的时间应该是同步的，在这里我们发现狭义相对论的对称性被破坏了。为什么会这样呢？实际上我们刚刚忽略了一件事，那就是事件1发生的瞬间，双生子2速度发生变化，他非惯性了，而双生子1一直是惯性的，所以他们的对称性就是在这一刻被破坏的。在一个瞬间发生速度变化，加速度瞬间达到无穷大，这不合实际，不过却让问题变简单了。如上方左图，飞船转向发生前，双生子2认为的双生子1那里的同时对应事件2，但飞船转向发生后双生子2认为双生子1那里的同时对应事件3，由于转向是瞬间完成的，这是一个突变。事件2和3之间的时间差就是双生子2回到地球之后他们年龄的差距。这里狭义相对论的对称性被破坏是因为非惯性，而非惯性问题实际上已经不是狭义相对论的研究范畴了。
为了让上述问题更加符合实际，我们把双生子2的飞船转向改为在一段时间内完成。我们可以认为双生子2遇到了一个大质量天体，他进入了大质量天体的双曲线轨道，因此经过天体之后折了回来。于是双生子2的旅行可以分为两个匀速阶段（离大质量天体加速度忽略）和一个变速阶段。在大质量天体的附近，双生子2时间变慢了，双生子1由于远离大质量天体，并不存在这一问题，因此最终，双生子2更年轻了。这个问题也引出了我们下面要讨论的广义相对论。
8.9 Happy Thoughts 欣喜的想法
引力场仅仅是相对存在的，对于一个正从屋顶自由坠落的观察者，引力场并不存在。
——爱因斯坦 1907
相对论引力的难题
对于万有引力公式F=GMm/R^2，在相对论框架下会出现问题，R是多少，对于不同的观测者，由于尺缩效应，R并不一样。更麻烦的是，这个R应当何时测量？假设现在太阳突然被移到距离地球2AU的地方，地球的运动会突然对此作出反应吗？显然不会，因为信息的传播速度也不能超过光速。
我们先来看看库伦力的公式，F=kQq/R^2，它和引力公式形式很类似，其实麦克斯韦给出了电磁领域相对论版本的答案。假设现在一个电子在一个质子形成的电场中，如果质子被移动，那么电子并不会立刻做出反应，质子移动会产生电磁波，电磁波就像电场中的涟漪，当它到达电子时，电子受到的库仑力才会改变。
麦克斯韦在解决这个问题的时候利用了电荷守恒，Q和q是不变的，但是我们知道质量并不守恒，在引力作用中，守恒的是能量和动量。但即便如此，对于能量和动量，不同参考系的观测者看来它们并不是不变量，这和电荷还是不一样。引力问题比电磁力复杂得多。
引力究竟是什么？我们如何测量引力场的强度？还是先对比库仑力，如果想知道一个场源电荷在某处引起的力场，很容易想到我们可以拿一个检验电荷放在这里，用它受到的力除以它的电荷。但是这样有个问题，电荷同时会受到万有引力，如何区分这两种力呢？我们可以用两个等量相反电荷的依次放在这一地点，他们所受的力的差值可以消除引力的影响，除以2再除以电荷量就是该点的电场强度。但是对于万有引力，不存在互斥的情形，可见对于引力的测量，我们找不到合适的操作性定义。
等效原理（the principle of equivalence）
爱因斯坦提出，对于引力下自由下落的观测者而言，引力并不存在，在太空中，天体都是自由下落状态的。反过来，一个加速运动的参考框架，可以起到和引力等同的作用，正如我们在电梯刚刚启动的时候感受到的那样。引力的一个独特的性质就是它赋予同一位置的所有物体同样的加速度，这一加速度与物体的性质无关（引力质量=惯性质量）。在一个事件中，我们可以通过选定一个适当的加速参考系让引力消失。
不过引力仅仅是加速度吗？地球是一个球，地球上各地的引力加速度是不一样的，引力场在时间和空间里的变化也正是引力区别于加速参考系之处，实际上也正是不同地方的引力的不同导致了潮汐力的出现，因此可以说潮汐力才是真正的引力。
引力红移（gravitational red shift）
上面是两个飞船，左边的在空间中，没有引力，但是向上做加速度为g的加速运动；右边的停在地面上，当地重力加速度是g。根据等效原理，这两个飞船是完全等同的，例如我们在两个飞船同一位置同样速度抛一个球，它们会做相同的抛物线运动。
现在，我们左边飞船底部有一个蓝灯，它向上发出蓝光。假设此刻飞船速度是v（这个v无关紧要，因为完全可以选定一个惯性系让v等于0），飞船的顶部有一个观测者速度也为v且他一直做匀速直线运动不加速。如果飞船做匀速运动，那么显然不会出现频移，因为观测者相对发射源静止，但是现在飞船在加速，光线到达观测者耗时为H/c（H是飞船高），到达观测者时飞船的速度变成了v+gH/c，这时，波源以gH/c的速度远离观测者，根据多普勒频移公式，此时观测到的波长
, 波长边长，出现红移。右边和左边等效，所以，由于地球引力，从飞船上方观察下方的光线也发现红移现象。当然飞船上方的引力加速度并不是0，只是比下方小一点点，所以红移很微小，测出来是很困难的。这仅仅是一个例子，对于其他物理现象也是如此，从上往下看，会发现钟表走得更慢。
1959年，Pound Rebka在Jefferson实验室的塔中利用原子对特定频率光谱的吸收测定了引力红移的量，结果和爱因斯坦的等效原理很吻合。
http://en.wikipedia.org/wiki/Pound%E2%80%93Rebka_experiment
现在我们的很多设备都会考虑到这一现象的影响，例如GPS系统就要顾及引力红移的因素。
8.10 Gravity is Geometry 引力是几何学
爱因斯坦提出上述理论之后，他发现背后的数学很复杂，不过比牛顿幸运的是，他发现自己想要解决的一些难题已经在一些数学家那里被解决了，在和Remon讨论之后，他很快发展出了广义相对论（the theory of general relativity）。广义相对论的数学很复杂，我们不会涉及技术性问题，只会直接给出结论。
引力
在小区域的时空里，在正在自由下落的惯性观测者看来，引力不存在。可以有很多观测者，这些观测者可以有不同的速度，他们的关系已经由洛伦兹变换确定。真正让引力变得有意义的在于潮汐力，即随着时间和空间的变化，引力也在变化，就是说，不同地方的局部惯性观测者是不同的。如果有两个相距人都开始向地球做自由落体，他们都会发现说对方是非惯性的，当然真实发生的事情是他们都在向地心做加速运动，他们的加速度差异——潮汐力才是真正的引力。
给定一个点一个初速度，这一刻，世界线开始，然后让引力发挥作用，物体开始在引力下运动，物体会画出一条唯一确定的世界线。
几何学
上面讲到的问题非常类似于19世纪到20世纪初发展起来的一些几何学理论，这些几何学主要研究的是弯曲空间（curved space）而非平直空间（flat space）。
小区域内的弯曲空间可以当成平直空间，可以用普通坐标系描述。
从特定点出发，可以画出任意方向的直线，这些直线在局部可以经旋转而重合。但是，由于曲率的存在，在别的地方，这些直线不能旋转重合。
给定一个点和一个初始方向，有唯一确定的测地线（geodesic），它类似于平直空间里的直线，是连接两点的最短程线。
弯曲在小区域内可以看作平直空间，但是一定距离之外的空间的形状被某种和坐标系无关量改变了，这个量就是曲率（curvature）。
下面举两个弯曲二维空间的例子，弯曲的三维空间只能用四维空间来直观描述，我们无法做到。
例1：正曲率——地球球面
我们这里把地球近似简化成一个正球，地球上每一点都是等同的。地球表面是一个弯曲的二维空间。
对于地球上的小区域，我们完全可以看成平面，例如我们可以用直角坐标精确地表示位置，小区域的平面地图也是非常精确的。但是平面上的全球的地图将不可避免地发生变形。
地球表面的直线——即测地线是沿着大圆的，显然子午线是测地线。
为了便于描述，我们假定从极点出发，我们可以在极点选择走任何一条直线（子午线），如果两个人同时从极点出发，沿着不同的子午线走，一开始，他们会像在平面上那样越来越远。但是很快他们会发现相互之间的距离不会像平面那样无限增大，而是有一个限度，它们在赤道距离达到最大后又开始靠近，最后于另一个极点再次相遇。球面是正曲率曲面，测地线分开的程度比平面小。
例2：负曲率——双曲面
这里主要注意的一点是，同一点不同方向的测地线，在距离稍远的地方就会相差很多，对于负曲率曲面，测地线分开的程度比平面大。
引力和几何的类比
惯性世界线（Inertial worldlines）——测地线（geodesics）
洛伦兹变换——旋转
间隔（interval）s^2=c^2*t^2-x^2——距离（distance）r^2=x^2+y^2
引力——曲率
上面间隔和距离分别是洛伦兹变换和旋转下的不变量，不过它们的表达形式不一样，一个正号一个负号，这一点决定了引力和几何学会有很多不同。
可以认为大质量天体使时空弯曲，物体沿着弯曲时空里的直线运动。
下图是一个常用来直观展示的图，一个橡胶板上放一个保龄球，橡胶板因此变形，然后丢一个乒乓球进去滚动，乒乓球开始绕着保龄球旋转。这里其实有很多误导，主要是在地球的引力下，保龄球向下沉得太多，这种特别突出向下的情况在实际中并不存在。
注意事项（caveats）
在广义相对论中，被扭曲的是时空而不是空间，上图表达的仅仅是二维空间的扭曲，但实际上是三维空间加时间的扭曲。在静止的时空里，空间是恒定的，但一般来说并不是这种情况。行星围绕恒星的运动，并不沿着扭曲空间的测地线，而是扭曲时空的测地线。一套通用的坐标是找不到的。
下图是一个更好的直观图
这是一个大质量天体——譬如恒星造成的空间扭曲，是弗拉姆抛物面（Flamm's paraboloid）。可以看出恒星周围的空间是相当对称的，你可以把它分解成球，根据不同的区域分配球的大小。我们在这里（二维）没有画球而是画了圆。 如果空间是平直的，这些圆之间的距离就是它们半径的差值，但是在弯曲空间里并不是这样，这些圆的距离比它们的半径差更大，而且越接近引力体，差距就越明显。
广义相对论（general relativity）
把引力几何化仅仅是第一步，接下来需要写成数学表达式，这将告诉你质能将时空扭曲的根源。正如电荷是电场的源头，质能是时空弯曲的源头。就像电磁波，质能在时空中产生了涟漪形成波，以光速传播信息。
引力方程式
左边的量表示时空里某个特殊点的扭曲，G是万有引力常数，c是光速，T是能量-动量的张量。右边的T就像电荷，T的改变会影响左边——引力场的回应。
这是一个微分方程，其中一个解是惯性运动，天体仅仅在引力作用下沿着扭曲时空的测地线运动。正如解麦克斯韦方程可以得到电荷守恒，解爱因斯坦的这个方程可以推导出能量和动量守恒。
当时空曲率很小（不接近大质量物体）、运动速度远小于光速时，广义相对论的结果和牛顿定律的结果几乎一样，比如我们看一下势能函数，可以从中找到很多我们熟悉的东西。
最后还有一点要提出，这一点在电磁领域并不存在。地球围绕太阳旋转这个体系的总质量小于地球和太阳的质量之和，因为地球从距离太阳无穷远处到现在的位置必定会释放能量，只能守恒，所以质量必然减小了，这类似于强相互作用的质量亏损。换句话说，引力场携带能量，引力场也会受引力作用，这就好比电磁作用中发出的光子带电了，然后又产生了新的电磁叠加在原有电场之上。因此，爱因斯坦的引力方程是非线性的，它比电磁作用的方程复杂得多，直到今天，这仍然是一个很活跃的研究领域。
8.11 GR in Astronomy 天文学中的广义相对论
水星轨道的进动
第一个对广义相对论进行检测的是爱因斯坦本人，他1916年指出水星轨道势能需要修改。牛顿的引力公式是F=-GMm/R^2，水星轨道应该是一个封闭的椭圆。如果上述公式稍有改变，就不再会是这样的结果。实际上早在爱因斯坦提出修正轨道之前半个世纪，水星轨道的进动就已经被观测到，水星轨道每世纪进动1.5°，其中有太阳扁率和其他行星摄动的因素，但是经过计算，这些摄动造成的进动应该是43’，那么剩下的进动来自哪里呢？爱因斯坦修正后的引力公式F=-GMm/R^2*(1-v^2/c^2)，发现，经过相对论修正，水星轨道会再进动43’，这样加起来就符合观测结果了。
这一现象不仅见于行星绕恒星公转的情况，在一些临近双星上表现得更加明显。
在很接近的双星系统中，广义相对论更加重要。
引力探针B （gravity probe B）
探测器由于时空弯曲和地球旋转产生的偏移量，和广义相对论吻合。
光线偏折（light deflection）
在引力场中光线也会发生弯曲，根据广义相对论，偏折的角度
.光线偏折将使我们能看见太阳后面的恒星，不过太阳太亮，幸运的是爱因斯坦发表论文后3年——1919年，爱丁顿（Eddington）利用一次日全食做了观测，下图右边是他拍摄到的照片（负片），照片测量的结果符合广义相对论的预言。
引力透镜（gravitational lensing）
上图是哈勃天文望远镜拍摄的图，其中黄色亮点是星系中的星团，它们距离我们比较近，而用绿色圈出的比较怪异的东西是离我们很远很远的星系，它们之所以显得怪异是因为它们的光线经过大质量天体时被偏折了，甚至有些星系会显现出两个像。这就是引力透镜效应，引力透镜在现代天文学中非常重要，我们可以光线的偏折度来计算看不见的天体质量，这可以用来探测太阳系外行星（exoplanet）以及暗物质（dark matter）。
天鹰座（Aquila）的毫秒级脉冲双星PSR1913离地球6400pc，脉冲周期59ms. 两颗中子星距离很近且轨道很扁，轨道长半轴2.8倍太阳半径，两颗星最近仅仅1.1被太阳半径。当两颗星接近时，由于伴星的引力红移，脉冲被延迟。此外还可以测到近星点的进动，与广义相对论的预测完全一致。
引力波
根据广义相对论，两颗中子星互相旋转会产生引力波（gravitational wave）损失能量，它们会越来越近，轨道周期越来越短。据估计这两颗星在2.5e8年后会合并，形成更大的中子星或黑洞。地球绕太阳旋转也会产生引力波，不过很弱，地球因此而对太阳的靠近量微弱到不可测。
现在我们有一些探测器例如LIGO正在试图探测引力波，不过到目前还没有探测到，据估计如果发生中子星合并这样剧烈的事件，我们的探测器将有可能探测到引力波。现在我们除了电磁望远镜之外有了别的手段，一个是中微子探测，另一个就是引力波探测。
8.12 Black Holes 黑洞
如果中子星的质量大到中子简并力也无法阻止它坍塌，那么它就会完全坍塌。现在，我们不讨论恒星内部发生的事情，势能释放超新星爆发之类，我们先来看看彻底坍塌之后对周围的影响。
注：本节介绍的是最简单的无旋转不带电的球对称黑洞——史瓦西黑洞，转动的黑洞叫做克尔黑洞，更加复杂。
引力红移（gravitational redshift）
近地表，我们有公式λ=λ0(1+gh/c^2)。在距离地球很远的地方，我们有如下公式：
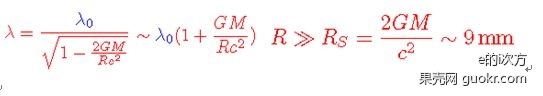
Rs被称为史瓦西半径（Schwarzschild radius），对地球而言这个半径是9mm。当R>>Rs时，红移量比较小，而当R接近Rs时，红移量趋于无穷大。对地球来说，你没法达到那里，你需要一个更加致密的天体。Rs和质量成正比，对于太阳来说，Rs是2.95km。对于中子星来说，它的半径大概是3-4个Rs，在这种情况下，从中子星发射出来的光红移会非常明显。
如果一个天体比中子星更致密，达到了史瓦西半径，就形成了黑洞，这时红移为无穷大。这意味着当你从远处看一个落向黑洞视界（horizon, 史瓦西半径）的物体，你会发现物体永远也落不到视界上，这是因为时间膨胀，从远处看，接近视界的地方时间趋于静止。同时由于无限红移，无论多亮的物体，在你看来都会变得越来越暗。在视界以及视界内部，没有光线可以逃出去。如果你在视界附近，当你回头你会发现物体都落向你，光线会强烈蓝移，外面的时间比你的时间快，如果在很接近视界的地方，你能够看到宇宙的终结。
我们不知道恒星内部发生了什么，我们只知道从很远的地方看坍塌似乎停止了，时间变慢以及红移。我们不会等到恒星完全坍塌成黑洞，因为这在我们看来需要的时间是无穷大。
更近一些
黑洞3Rs外可以存在稳定轨道，轨道周期很短。小于3Rs时不存在稳定轨道，任何极小的扰动都会干扰物体，使物体落向黑洞或远离黑洞。在R=1.5Rs的地方，随着光线偏折变得非常厉害，甚至光将开始环绕黑洞运动，不过这个轨道是不稳定的。你可以叫这里光球，其实中子星也可以有光球。
在很近的地方，潮汐力将变得很大
~可见黑洞质量大一些，潮汐力反而会小一些，太阳质量的黑洞能够完全将你撕碎，不贵40亿太阳质量的黑洞将不会，甚至你不会意识到你正在通过视界。
视界（horizon）
在视界上，时间是静止的，你永远不会到达那里，不过仅仅在远处看来是这样。如果你真的到了那里，你会看到恒星没有停止坍塌，刚才说恒星看起来停止坍塌因为恒星坍塌并不发生在我们的时间里。
我们并不能用很远之外地方的坐标系来研究它，因为在很远的地方看来光无限红移消失了，时间变得无限慢。我们这里使用的是克鲁斯卡尔坐标系（Kruskal–Szekeres coordinates），你会发现视界是光的世界线，这也解释了为什么光不能离开这里。如果你在视界之内发射光线，光不可能到视界之外，因为要到视界之外，它必须超过光速。一旦进入视界，任何东西都无法再出来。这里很奇怪，在近处看视界不是一个地方（像从远处看那样），而是一个像光一样的东西，它在不同的时间对应不同的位置。
在克鲁斯卡尔坐标系中，在径向坐标可以从正无穷大连续变化到零，中间经过视界。这个连续变化对应着上图中蓝色的双曲线族，其中经过R轴的双曲线对应着视界外的情形，经过T轴的双曲线对应着视界内的情形，双曲线的两条渐近线对应着视界。灰色区域边界对应着黑洞的奇点，而在那以外的部分（图中的灰色区域）时间和空间坐标都没有定义。
wiki克鲁斯卡尔坐标系 http://en.wikipedia.org/wiki/Kruskal%E2%80%93Szekeres_coordinates
视界之内
从很远的地方，我们发现接近视界的光静止了。但是如果你自己跌入黑洞，你会在有限的时间里通过视界。进入视界之后，时空坐标互换，原来的时间t成为空间坐标，原来的径向坐标r成为时间坐标，黑洞内部的等r面不再表示球面，而成了等时线。在视界之内，时间方向指向r=0的奇点处，所以任何物质都将不可抗拒地向奇点移动，并在有限的时间里到达奇点。进入视界的人并不会发觉时空的变化，他只能感受到越来越大的潮汐力，最终在奇点，潮汐力增大到无穷大，任何物质都会被撕碎。
在奇点，相对论方程失效了（显示了广义相对论的不完备性），谁知道会发生什么呢？
8.13 Journey to a Black Hole 黑洞之旅
一个黑洞之旅的模拟。
http://casa.colorado.edu/~ajsh/schw.shtml
如上，30倍太阳质量的黑洞，Rs大约100km。旁边有3个恒星，蓝色的60倍太阳质量的年轻主序星和黑洞组成一个双星系统。飞船路径已经标出。
接近黑洞
我们从距离黑洞1亿千米的位置出发，100Rs黑洞透镜效应制造了爱因斯坦环，这是蓝色恒星的光在黑洞引力之下弯曲形成的，继续接近会看到所有恒星的多个透镜影像。在3Rs上（最低稳定轨道），可以看到光线偏转得很厉害，以至于视界的两极都可见。注意这里为了让你看见，视界被加上了红色格子，实际情况当然不是这样，实际视界是不可见的。
环绕黑洞
现在降落到2Rs轨道上，以0.7倍光速移动，可以看到加强的引力透镜效应，出现了恒星的多重图像。从远处看，我们的轨道周期是8毫秒，不过我们认为是4毫秒，因为我们现在在2Rs位置，引力红移的因子是
，0.7倍光速造成的因子也是。潮汐力是100g左右，你的脚会以你100倍的重量扯你的头。在距离我们400千米远处静止释放的白色球状探测器在潮汐力作用下被拉到变形，接近史瓦西视界时，变红变慢，最接近视界时看起来停止下落、变红，融入视界。落入奇点
我们继续减速，穿越视界，在视界上会遇到在我们之前进入视界的人，在视界上潮汐力会达到100万g，0.1毫秒后会撞上奇点。
8.14 Black Holes in Astronomy 天文学中的黑洞
黑洞的光无法逃逸，所以不能被看见，但可以通过对周围物体强烈的引力效应被发现，恒星坍塌成黑洞通常需要有一颗距离极近的伴星进行质量转移。当质量转移进行时，落入黑洞的物质形成了吸积气盘，盘延伸到3Rs之外，在这个半径之外的物质剧烈摩擦（之内没有稳定轨道），强烈发热，而发出X射线。借由对这类X射线的观测，可以间接发现黑洞。
第一个被发现的黑洞候选者是天鹅座X-1（Cygnus X-1），位于天鹅座的X射线双星，X射线源的近轨道是一颗O型超巨星，我们发现它在环绕着某个不可见的天体运动。根据多普勒频移的观测结果，我们算出不可见的天体质量在10-20倍太阳质量。同时X射线源的闪烁频率大约是1ms，任何物体的速度都不可能超过光速，这样我们可以确定闪烁X射线的物质距离不可见天体的中心距离在3000km之内。3000km对于一个恒星来说太小了，除了中子星其他恒星都不会这么小。但是中子星的质量不可能超过3倍太阳质量，所以我们有充分的把握认为它是一个黑洞。另一个黑洞在仙女座星系（Andromeda galaxy）被发现。
大黑洞
我们目前没有发现黑洞质量的上限，黑洞可以是几个太阳质量到100个太阳质量，在这之后有个断层，然后就是几百万到几十亿太阳质量的巨型黑洞，它们在星系的中心。从一百万太阳质量到几百万太阳质量之间也许会有其他类型的天体，不过我们尚未发现。
银河系中心附近的恒星运动表明银河系中心可能有10^6-10^7太阳质量的巨大黑洞（Sagittarius A*），似乎多数星系的核心都有大黑洞，M31仙女座星系中心的黑洞质量有几十亿太阳质量。巨型黑洞应该不是恒星演化形成，具体成因尚不清楚。星系是我们下周的主题，是黑洞聚集了星系还是星系形成了黑洞？
8.15 Black Holes in Theory 理论中的黑洞
关于黑洞的事实
黑洞无毛定理（the black hole no hair theorem）：无论什么样的黑洞，其最终性质仅由几个物理量（质量mass、角动量angular momentum、电荷electric charge）惟一确定。在形成过程中，黑洞的其他所有性质（物质构成、温度、形状）的信息在之前被辐射掉。黑洞是坍塌的中子星，当中子星形成时携带了足够的角动量来产生脉冲，我们估计大部分黑洞在快速旋转。我们的黑洞之旅忽略了角动量的影响。
霍金（Hawking）和彭罗斯（Penrose）的研究表明奇点是真实存在的，广义相对论从非奇异的初始条件产生了奇点，这意味着广义相对论是不完整的，我们没有关于引力的最终论断。
宇宙监督假设（cosmic censorship conjecture）认为我们无法看到黑洞中心的奇点发生了什么，视界内的东西不会对我们产生任何影响，我们不必去研究它。但是，这个假设可能错了，最新研究表明可能存在没有隐藏在视界里的裸奇点（naked singularity）。
虫洞（Wormholes）
再次看一下黑洞的图，III是白洞，如果想进如白洞，必须超过光速，所以只能有东西从白洞里出来，不能有东西从白洞里进去，其性质与黑洞完全相反，不断地向外围喷射各种星际物质与宇宙能量，是一种宇宙中的喷射源。不过目前还没有发现白洞存在的证据。
上图左右两边都是黑洞外部，它们仅仅一个点相连。这个相连的点是虫洞（Wormhole），又称爱因斯坦-罗森桥（Einstein—Rosen bridge），是宇宙中可能存在的连接两个不同时空的狭窄隧道。它在时空中太不稳定，以至于光都无法通过。我们正在试图寻找得到大虫洞的办法。
量子黑洞（quantum black holes）
这个理论再次归功于霍金。根据量子理论，任何场都在辐射能量，黑洞也在一样，被称为霍金辐射，这不是广义相对论而是量子场的性质。黑洞视界附近波动的大曲率的存在意味着黑洞在辐射，霍金计算指出黑洞辐射是黑体辐射，黑洞有温度，后来发展出黑洞热力学 （black hole thermodynamics）。较小的黑洞辐射更大，温度与质量成反比。辐射的能量来自质量，失去质量温度又会上升，黑洞是个奇怪的负比热（negative specific heat）物体，因此黑洞的终结会很戏剧，会是一个大爆炸，黑洞会完全蒸发消失。对于5倍太阳质量的黑洞，完全蒸发的时间会是1e62年，考虑到我们宇宙的年龄只有1.5e10年，黑洞的爆炸似乎不是我们需要担心的问题。不过，微型黑洞会蒸发更快，我们正试图造出几厘米甚至质子大小的微型黑洞以对它进行观察研究。
相对论通俗演义(包括PDF)_科学论坛_天涯论坛
bbs.tianya.cn › 科学论坛 › 科普天地
轉為繁體網頁
轉為繁體網頁
而在狭义相对论中，闵氏时空是伪欧的，速度空间是双曲空间 ...
phymath999.blogspot.com/2015/03/blog-post_79.html
轉為繁體網頁
轉為繁體網頁
[PDF]7.1-6属7.1节坐标和线元
202.38.64.11/~jmy/documents/answers/sol-ch07.pdf
轉為繁體網頁
轉為繁體網頁
正在载入资料... - My China News Digest
my.cnd.org/modules/newbb/viewtopic.php?...id...
轉為繁體網頁
轉為繁體網頁
[DOC]高等几何与解析几何的诞生 - 天津师范大学精品课程
59.67.71.237:8080/xjp/.../高等几何与解析几何的诞生.do...
轉為繁體網頁
轉為繁體網頁
Week 8 Relativity and Black Hole 相对论和黑洞| Introduction ...
mooc.guokr.com/note/15930/
轉為繁體網頁
轉為繁體網頁
No comments:
Post a Comment