兩向量垂直的充要條件是向量內積等於零。理由:
[線性代數]自共軛算子的光譜分解的idea(Spectral Theory)
In 線性算子、線性代數、泛函分析 on 06/06/2012 at 10:15 下午
假設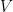 是一個內積空間(複內積空間或實內積空間),並且
是一個內積空間(複內積空間或實內積空間),並且 是其上的線性算子。如果
是其上的線性算子。如果

 ,那麼我們稱這個線性算子是自共軛(self-adjoint)的或Hermitian。自共軛算子的光譜分解主要來自於兩個部分:第一,二次曲線的分類。第二, Fourier對熱方程的解。二次曲線是形如
,那麼我們稱這個線性算子是自共軛(self-adjoint)的或Hermitian。自共軛算子的光譜分解主要來自於兩個部分:第一,二次曲線的分類。第二, Fourier對熱方程的解。二次曲線是形如
 所定義出來的平面曲線(plane curve)。在中學的時候我們學習過,形如
所定義出來的平面曲線(plane curve)。在中學的時候我們學習過,形如 是圓(
是圓( )而
)而 是橢圓,
是橢圓, 是雙曲線,
是雙曲線, 是拋物線,
是拋物線, 是相交于圓點的兩條直線。而我們要如何的去分析
是相交于圓點的兩條直線。而我們要如何的去分析 進而得到曲線的類形呢?這問題就是二次曲線的分類。
進而得到曲線的類形呢?這問題就是二次曲線的分類。
熱方程式形如 的偏微分方程。Fourier透過分離變數
的偏微分方程。Fourier透過分離變數 得到了兩個常微分方程:
得到了兩個常微分方程:
(1)
(2)
進而得到了熱方程的解。我個人傾向使用Fourier的例子來說明譜分解是怎麼來的,想法真得很簡單。
假設我們令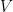 表示所有定義在
表示所有定義在![[0,2\pi] [0,2\pi]](https://s0.wp.com/latex.php?latex=%5B0%2C2%5Cpi%5D&bg=FFFFFF&fg=000000&s=0) 並且滿足
並且滿足 的二次可微分實值函數所成的向量空間。換句話說,
的二次可微分實值函數所成的向量空間。換句話說,
![V=\{f\in D^{2}([0,2\pi]):f(0)=f(2\pi)=0\}. V=\{f\in D^{2}([0,2\pi]):f(0)=f(2\pi)=0\}.](https://s0.wp.com/latex.php?latex=V%3D%5C%7Bf%5Cin+D%5E%7B2%7D%28%5B0%2C2%5Cpi%5D%29%3Af%280%29%3Df%282%5Cpi%29%3D0%5C%7D.&bg=FFFFFF&fg=000000&s=0) 令
令 定義為
定義為![T[y]=-y'' T[y]=-y''](https://s0.wp.com/latex.php?latex=T%5By%5D%3D-y%27%27&bg=FFFFFF&fg=000000&s=0) 。則
。則 是
是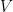 上的線性算子。我們令
上的線性算子。我們令 ,那麼
,那麼 為
為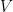 中的成員族(family)。如此一來
中的成員族(family)。如此一來
![T[s_{n}]=n^{2}s_{n} T[s_{n}]=n^{2}s_{n}](https://s0.wp.com/latex.php?latex=T%5Bs_%7Bn%7D%5D%3Dn%5E%7B2%7Ds_%7Bn%7D&bg=FFFFFF&fg=000000&s=0) 。
這個發現誘發出了eigenvalue與eigenvector的概念。
。
這個發現誘發出了eigenvalue與eigenvector的概念。
定義:假設 是一個線性算子,如果存在一個非零向量
是一個線性算子,如果存在一個非零向量 與一個複數(或實數)
與一個複數(或實數) 使得
使得 ,則我們稱
,則我們稱 是
是 的一個eigenvector且
的一個eigenvector且 是
是 所對應的eigenvalue。
所對應的eigenvalue。
另一方面,如果 是二次可微分的函數,並且
是二次可微分的函數,並且 在
在 時都為零,利用分部積分得公式(integration by parts)與
時都為零,利用分部積分得公式(integration by parts)與 可以得到
可以得到
 在使用一次分部積分與
在使用一次分部積分與 ,我們可以推得
,我們可以推得
 于是如果我們定義
于是如果我們定義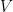 上的內積如下:
上的內積如下:
 那麼我們發現上面的積分式等價於
那麼我們發現上面的積分式等價於

 。於是在此內積意義下,
。於是在此內積意義下, 成了一個自共軛的算子。同時我們還發現,
成了一個自共軛的算子。同時我們還發現, 構成了
構成了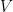 的一組直交集合(orthogonal set):利用積化合差的公式與
的一組直交集合(orthogonal set):利用積化合差的公式與 的性質我們可以證明
的性質我們可以證明
 附註:兩向量垂直的充要條件是向量內積等於零。理由:
附註:兩向量垂直的充要條件是向量內積等於零。理由: 其中
其中 是這兩向量的夾角(在任河內積空間中,你都可以這麼想)。
是這兩向量的夾角(在任河內積空間中,你都可以這麼想)。
然後你開始去想,是不是能將這樣的想法推廣到更一般的內積空間與其上的自共軛算子呢?在有限維內積空間上的自共軛算子,我們的確有這樣的理論。
熱方程式形如
(1)
(2)
進而得到了熱方程的解。我個人傾向使用Fourier的例子來說明譜分解是怎麼來的,想法真得很簡單。
假設我們令
定義:假設
另一方面,如果
然後你開始去想,是不是能將這樣的想法推廣到更一般的內積空間與其上的自共軛算子呢?在有限維內積空間上的自共軛算子,我們的確有這樣的理論。
No comments:
Post a Comment