路径积分的基本思想我的理解是某一时刻的波函数可以由不同历史的波函数加权求和得出,不知道是否准确?
是否代表时间相对其他空间维度具有特殊性?
路径积分能不能理解为某种傅立叶变换?
如何直观或者形象地(比如通过某个例子)理解路径积分?
~~分割线~~
感谢各位的解答!
关于第一点,由于概念混淆造成误解请各位包涵。此处将“某一时刻的波函数”改为“两点之间的概率幅(transition amplitude)”不知是否更为准确?
关于第三点,与傅立叶变换的联系一方面是因为公式的相似性,另一方面是因为积分变换与微分方程的关系,希望有朋友解答。
关于第四点,光的波动性与无穷多个双缝干涉都非常有意思,希望可以有朋友解释更多细节。
是否代表时间相对其他空间维度具有特殊性?
路径积分能不能理解为某种傅立叶变换?
如何直观或者形象地(比如通过某个例子)理解路径积分?
~~分割线~~
感谢各位的解答!
关于第一点,由于概念混淆造成误解请各位包涵。此处将“某一时刻的波函数”改为“两点之间的概率幅(transition amplitude)”不知是否更为准确?
关于第三点,与傅立叶变换的联系一方面是因为公式的相似性,另一方面是因为积分变换与微分方程的关系,希望有朋友解答。
关于第四点,光的波动性与无穷多个双缝干涉都非常有意思,希望可以有朋友解释更多细节。
按投票排序按时间排序
8 个回答
没有一个人从Kolmogorov定义出发么?
对于一个事件我们可以很简单地说各个概率是多少 P(A);
两个事件?连续事件概率 P(A_1, A_2);(这里取事件是离散的,如果是连续的应该还有dA_1dA_2)
更多也好办,可以推广;
到无穷的极限是否有一个合适的定义?如果可以有一个坐标图画出,就是在横坐标为时间,纵坐标为事件上的一条轨迹(以函数f(t)表示),任取(当然是有预先分布的)的一条曲线(只要一个时间只有一个事件)落在此轨迹附近的概率是P[f(t)]Df,其中Df就是离散情况下df_1df_2...,对应空间一定体积。
归一性\int P[f(t)]Df = 1
函数/泛函平均值<F[f]> = \int F[f(t)] P[f(t)]Df
这大概是我第一次在量子力学课以外还发现统计也可以这么玩。
对于一个事件我们可以很简单地说各个概率是多少 P(A);
两个事件?连续事件概率 P(A_1, A_2);(这里取事件是离散的,如果是连续的应该还有dA_1dA_2)
更多也好办,可以推广;
到无穷的极限是否有一个合适的定义?如果可以有一个坐标图画出,就是在横坐标为时间,纵坐标为事件上的一条轨迹(以函数f(t)表示),任取(当然是有预先分布的)的一条曲线(只要一个时间只有一个事件)落在此轨迹附近的概率是P[f(t)]Df,其中Df就是离散情况下df_1df_2...,对应空间一定体积。
归一性\int P[f(t)]Df = 1
函数/泛函平均值<F[f]> = \int F[f(t)] P[f(t)]Df
这大概是我第一次在量子力学课以外还发现统计也可以这么玩。
量子力学有不同的表述方法。在经典的Sakurai的教材,是用正则量子化(canonical quantization)的方法,用的主要是算符和量子态、波函数等;另一方法便是路径积分(path integral)。二者是等价的。
如果用路径积分,我们便不用波函数。不过,正则量子化中的结果(如各能级的波函数)有时也因綫性代数的原因而被使用,但原则上是独立的。波函数所展现的随机性,在路径积分可以得到体现,因为波函数的运动方程就是古典解中的结果而同时也是量子解中的期望值,路径积分很自然地把量子力学和古典力学连在一起。而路径积分算出的关联则用以描述古典力学没有的随机性。
至于时间是不是特别,我不敢说,但路径积分是泛函积分。在量子力学中,作用量是位移的泛函,而位移通常是时间的函数。当到了量子场论时,作用量也是泛函,但当中的函数是位移(或动量)及时间(或频率)的函数。到了统计场论,时间很多时候没有特别意思。
路径积分某程度上是概率分佈的泛函,但在量子力学中因为虚数i的存在而不明显;但到了统计场论,这个积分算出的就是Helmholtz自由能。
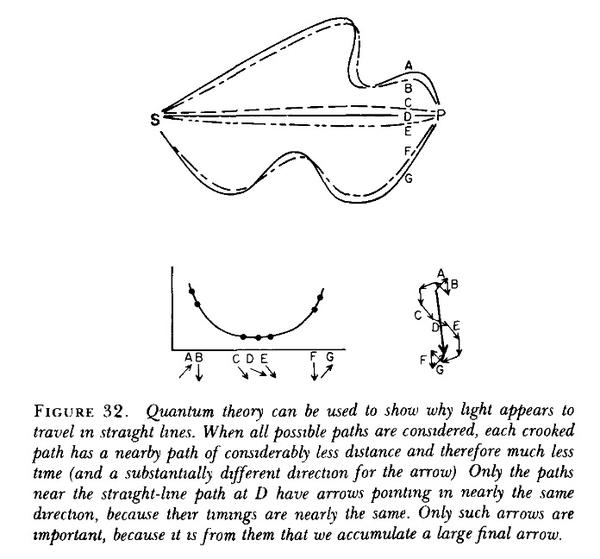
关于第四个问题,费曼在其《理性边缘的物理》(QED: The Strange Theory of Light and Matter)有很好的描述。他用光子的相(phase)去描述各样波动学的结果(费曼本人不相信波粒二象性,他认为所有东西都该用粒子描述)。
书目推介:
如果用路径积分,我们便不用波函数。不过,正则量子化中的结果(如各能级的波函数)有时也因綫性代数的原因而被使用,但原则上是独立的。波函数所展现的随机性,在路径积分可以得到体现,因为波函数的运动方程就是古典解中的结果而同时也是量子解中的期望值,路径积分很自然地把量子力学和古典力学连在一起。而路径积分算出的关联则用以描述古典力学没有的随机性。
至于时间是不是特别,我不敢说,但路径积分是泛函积分。在量子力学中,作用量是位移的泛函,而位移通常是时间的函数。当到了量子场论时,作用量也是泛函,但当中的函数是位移(或动量)及时间(或频率)的函数。到了统计场论,时间很多时候没有特别意思。
路径积分某程度上是概率分佈的泛函,但在量子力学中因为虚数i的存在而不明显;但到了统计场论,这个积分算出的就是Helmholtz自由能。
关于第四个问题,费曼在其《理性边缘的物理》(QED: The Strange Theory of Light and Matter)有很好的描述。他用光子的相(phase)去描述各样波动学的结果(费曼本人不相信波粒二象性,他认为所有东西都该用粒子描述)。

书目推介:
- R. P. Feynman, QED: The Strange Theory of Light and Matter:科普读物,但很值得看,物理内涵丰富
- R. P. Feynman, A. R. Hibbs, Quantum Mechanics and Path Integral:基本教材。但本人得坦白一下,除了最后一课读过外(因研究课题之故),本人未读过这一本。但随眼一看,觉得应该是好书。
- L. S. Schulman, Techniques and Applications of Path Integration:对路径积分的各类应用都涉猎,初学参考必备。
态空间维数有限时,可以用矩阵相乘时求和指标会遍历一个(离散的)路径来理解。
参见Mumford的这篇文章:http://www.dam.brown.edu/people/mumford/blog/2014/FeynmanIntegral.html
无限维的情形貌似目前没被很好的理解,作用量是二次型的时候可以看作是高斯积分的无穷维推广。。
参见Mumford的这篇文章:http://www.dam.brown.edu/people/mumford/blog/2014/FeynmanIntegral.html
无限维的情形貌似目前没被很好的理解,作用量是二次型的时候可以看作是高斯积分的无穷维推广。。
积分,本质上来说就是叠加。而路径积分,是对每条路径的贡献进行叠加,也可以说是将每条路径的几率叠加起来,就得到了从这一点到那一点的几率。而要描述一条路径,尤其是量子概念下的路径(多么诡异都是可能的)需要你将每一瞬间的位置都表述出来,就是说你的自变量:路径,是要由无限多个量才描述的清楚的,用数学的表达就是,一条路径可以表述为一个无限维度空间中的一个向量。所以,路径积分的自变量是个向量,积分结果是从某一点到另一点的几率密度。
何史提、知乎用户 赞同
- 量子力学的路径积分表述下应该是没有波函数这个概念的。
- 在非相对论量子力学中,时间本来就有特殊地位。相对论量子力学(量子场论)中的路径积分的「路径」已经不是一个 path 了,而是整个时空的 field configuration,其中时间和空间地位相似。
- 含源路径积分(配分函数)可以看作是
的傅里叶变换:
,至于这有什么意义,我也不知道。
- 光的波动性。
知乎用户、匿名用户、知乎用户 赞同
2.
量子力学里面的时间,确实有特殊性。
这是为什么发展相对论场论的原因,在泛函积分里,时间就不特殊了。
3.
路径积分和傅里叶变换没有依存关系。
傅里叶是工具,哪里都可以用。
1+1=2 是工具,哪里都可以用。
1.
路径积分是种计算方法,它的出现来自于费曼的灵感,不来自于某种对于概念的堆砌和逻辑的思辨。
只来自于费曼瞎算时的发现。
------------------
路径积分量子化是不同于正则量子化的另一种计算方法,算散射幅是主业,当然,你也可以用编时算符去算,没人拦着你。
物理学的发现,都是基于计算的发现(被调侃了,这么说不严谨,应该是,物理学的发现,是基于实验的发现,从实验现象出发,得到理论,靠的是计算,所以说是基于计算的发现。但再追究一层,还是基于实验的发现。这里强调计算是为了与纯粹逻辑概念演变相对比。),不是基于逻辑概念的发现,后者叫做哲学、玄学。
(有一个例外,只有一个例外,爱因斯坦,他是有了概念,很清晰了,然后用微分几何表述出来了,这是为什么爱因斯坦是神一般的人的原因。不过,你去看他的原始论文,没大扯概念,也全是在算啊算。)
量子力学里面的时间,确实有特殊性。
这是为什么发展相对论场论的原因,在泛函积分里,时间就不特殊了。
3.
路径积分和傅里叶变换没有依存关系。
傅里叶是工具,哪里都可以用。
1+1=2 是工具,哪里都可以用。
1.
路径积分是种计算方法,它的出现来自于费曼的灵感,不来自于某种对于概念的堆砌和逻辑的思辨。
只来自于费曼瞎算时的发现。
------------------
路径积分量子化是不同于正则量子化的另一种计算方法,算散射幅是主业,当然,你也可以用编时算符去算,没人拦着你。
物理学的发现,都是基于计算的发现(被调侃了,这么说不严谨,应该是,物理学的发现,是基于实验的发现,从实验现象出发,得到理论,靠的是计算,所以说是基于计算的发现。但再追究一层,还是基于实验的发现。这里强调计算是为了与纯粹逻辑概念演变相对比。),不是基于逻辑概念的发现,后者叫做哲学、玄学。
(有一个例外,只有一个例外,爱因斯坦,他是有了概念,很清晰了,然后用微分几何表述出来了,这是为什么爱因斯坦是神一般的人的原因。不过,你去看他的原始论文,没大扯概念,也全是在算啊算。)




No comments:
Post a Comment