对应于牛顿定律，量子力学中粒子运动的规律由薛定谔方程描述。量子力学与经典力学不同的是，牛顿方程描述的是粒子运动的轨迹，是一条线。而薛定谔方程的解却是一个全空间的波函数y。波函数的平方被解释为粒子在空间出现的几率。既然是一种波，它最好的类比物当然是光波。从前面几节的叙述中我们已经了解到：几何光学中的最小作用量原理就是费马原理，那儿的作用量指的是“光程”。而光程又是什么呢？光程被定义为相应时间内光在真空中走过的距离，但它从本质上来说，所对应的是光波的相位。因为随着光的传播，光程增加，其相位便随之而周期性地变化
PDF]二极管激光泵浦的Nd:YAG 激光
pec.sjtu.edu.cn/ols/.../激光技术实验内容－近物实验.pdf
轉為繁體網頁
激光器由工作物质、谐振腔、泵浦源几部分组成。激光. 器按工作方式不同可 ... 7） 在聚焦镜后60 mm处是二极管激光的聚焦点，安装YAG棒。 1．二极管激光的输出功率.Brevet CN1105409C - 二倍频二极管泵激固体激光器- Google ...
www.google.fr/patents/CN1105409C?hl=fr&cl=zh
轉為繁體網頁
本发明提供了一个采用腔内二倍频方式的二倍频二极管泵激固体激光器，此固体激光器包括带有适当薄层的激光 ... 此谐振腔是在固体媒质(1)和元件(5)的反射薄层之间形成的。 ... 此外，如果散热性能很好的导热孔径安装在二倍频元件两个终端表面上。专利：激光二极管与谐振腔分离的整体冷却的激光器
www.chemyq.com › 专利
轉為繁體網頁
前言：一种激光二极管与谐振腔分离的整体冷却的激光器，包括主体，主体下半部设置走线及冷却管腔体，主体上半部设置用于安装激光二极管的腔体和用于安装谐振 ...Patent CN1046641A - 外腔半导体激光器- Google Patents
www.google.mg/patents/CN1046641A?cl=zh
轉為繁體網頁
一种外腔二极管激光器，包括一个具有线状反射平面的单块二极管激光器，它安装在一个具有两个端部的外谐振腔的一端上，该外谐振腔包括布置在谐振腔两个端部之 ...谐振腔半导体发光二极管(RCLED),resonant cavity light ...
www.dictall.com › 词典
轉為繁體網頁
您的位置：首页 -> 词典 -> 谐振腔半导体发光二极管(RCLED) .... 前者尺寸小、价格低，适宜安装在印刷电路板上；后者既可安装在仪器面板上，又可直接安装在印制 ...半导体二极管生产制造工艺,半导体二极管,谐振腔,非易失性 ...
www.51zlwx.com › 电子电器 › 电气元件 - 轉為繁體網頁
[4-BG61346] 全切面结玻璃钝化的硅半导体二极管芯片及其制造方法 ... P－I（光功率－电流）特性曲线的转折取决于激光器谐振腔的长度。 ... 布护封剂于该切面上；供应RCLED 谐振腔发光二极管_电子元器件_世界工厂网
product.ch.gongchang.com/d589430599.html
轉為繁體網頁
Firecomms RCLED元件（谐振腔发光二极管）是高速发光设计运行速度可达400 Mbps ... 不同的是替代品，塑料光纤具有大大降低安装成本，是不敏感的电磁干扰，
士不可以不弘毅，任重而道遠。分享http://blog.sciencenet.cn/u/daiyue Department of Physics, Fudan University
博文
徐一鸿《简明量子场论》笔记 （1）
|||
A. Zee的《简明量子场论》是一本很“讲物理”的场论书，用来入门非常合适。
首先，提供勘误链接，还有Clarifications。这份笔记中也会提到一些勘误。
这本书的书名叫“QFT in a nutshell”，直译过来应是《果壳中的量子场论》。现在有很多书名字都叫《果壳中的……》，据徐教授说，这类名字是他首创的。
场量子化有三种方法：比较常见的（比如说Peskin的书中一开始用到的）是正则量子化方法；本书则从路径积分方法讲起。（还有种方法我忘了。）I.2回顾了量子力学中的路径积分方法。
高斯积分
路径积分方法中经常要用到的数学运算：高斯积分，收录在Appendix 1中。其中出现的重要概念是Wick contraction，在P13的最后。求
的平均值，得到的结果是
，这个结果可以理解成6个
两两收缩，并对所有可能的收缩求和（后文中出现的
即表示这个求和）后得到的结果。每两个
收缩得到的结果是
，共有三对，即
。可能的收缩方式有
种，于是就得到。P15的Eq. (16)是Eq. (10)的推广，Eq. (18)是一个具体例子。在这里，Eq. (18)的意义是求矢量的4个分量的乘积的平均值，这样的说法比较难理解。实际上，这样的运算是用来求格林函数的。比如P47的Eq. (10)，如果令
，得到的自由传播的四点格林函数形式和P15的Eq. (18)一致，其物理意义是两个粒子传播的几率幅：等号右边第一项表示粒子1从坐标
传播到坐标
的几率幅（等于
），乘以粒子2从坐标
传播到坐标
的几率幅
。由于粒子的全同性，粒子1的末坐标也可能是，于是粒子2从坐标传播到坐标。另外还有第三种可能。把三种情况相加，就得到了两个粒子传播的总几率幅。
量子力学中的路径积分
量子力学中，粒子在两点间的运动没有确定的轨道。对于“没有确定的轨道”，一般人就直接理解成“没有轨道”了，而Feynman独辟蹊径，理解成“有许多条（事实上，是无限条）轨道”。路径积分的思想是：对于从一点运动到另一点的任意一条轨道（用
描述粒子运动的轨道），可以用
算出这条轨道的几率幅。其中
是作用量。粒子在两点间运动的总几率幅就是所有可能的轨道的几率幅之和。在经典极限下，
与
相比是巨大的，路径的微小改变会造成几率幅的剧烈振荡，使得临近路径的总几率幅会相互抵消掉。只有在取极值的路径附近几率幅不能抵消，这就是可以通过最小作用量原理求出的经典路径。
量子场论中的路径积分
量子力学中的研究对象是粒子，用坐标描述，量子场论中的研究对象则是场。所谓“场”，其实是一个数学概念。给定一个流形...或者不用“流形”这样的名词，我们生活的这个宇宙，每一点都可以用时间-空间四维坐标
来描述。在每一个时空点之上都给定一个数
，就得到了一个标量场。（也可以在每一点上给定一个矢量
，得到矢量场；还可以得到张量场等等。）当然，在场论中研究的场，都是一些有物理意义的动力学函数。
给定一个场，对不同的
，
不同，对时间的偏导数是场的动能；对空间的不同点，也不同，在场论中，对空间坐标的偏导数是场的动能。（其实应该是场的动量。但动能和动量实际上是同一四维矢量的分量。）总之，场的动能源于场在时空中的“变化”。除此之外，场自身也有相互作用，称为势能。比较重要的势能项，有
，其大小和场的平方成正比，系数
表征这项作用的强弱。这项势能是场因为自身存在即具有的能量。因为能量即质量，可见其实就是我们熟悉的[静止]质量。还有一个重要的势能项是和
成正比的。玻色气体中，每两个气体原子之间具有相互作用，假设相互作用能量是
。对于有
个原子的玻色气体，总相互作用能量就是
，很大时约等于
。考虑到
，玻色气体原子之间的相互作用其实就是相互作用。
知道了场的动能和势能，就能写出拉格朗日量以及作用量，即P17的Eq. (5)。同样，可以算出这个场的几率幅。量子场论中的路径积分方法是：认为所有的场函数都是可能出现的，计算出所有的几率幅，把它们相加，得到一个总几率幅。
和量子力学中类似，如果做微小变化，一般来说，会导致几率幅的剧烈振荡，使得“相邻”的贡献的几率幅会相互抵消——除非在作用量取极值处。因此，在场论中，同样可以用最小作用量原理，求出“实际出现的”场。对于标量场，这个“实际出现的”场满足Klein-Gordon方程。
源对场的作用
后文开始，保持和书上用的记号一致，用
代替
。
如P20所述。源
会和场
耦合，使得场和无源时不同。其原因在于源与场的耦合会改变场的能量，（比如说真空中放入一个电子，就会改变电磁场的能量，）从而改变场的几率幅。作用量取极值的场也会相应地变化。
这里有个观念上的变化。初次接触场，应该是中学里学到的电磁场。那时候，场被描述为源“产生”的东西，比如说电荷产生电场，电流产生磁场等。而按场论的观点，电荷和电场，一个是spin-1/2 Dirac场，一个是spin-1 电磁场，完全是两样东西。电荷并不会产生电场，而是因为和电场耦合，从而改变了电场——把电磁场从我们称之为“真空”的状态（这种状态我们以前认为是“没有场”的状态）变成另一种状态。
Wick转动
P12提到了Wick转动，是对时间轴做一个
的变换，其目的是把度规从闵氏的
变成欧氏的
，这样，在做积分时，可以“平等地”对待四个坐标，从而简化积分运算。有个需要注意的地方：变换不能是
，尽管这个变换也能达到同样的目的。其中的原因可以参考P23的Eq. (22)：积分项的奇点在复
平面的第二、四象限，Wick转动要避开奇点，因此只能是。
http://blog.sciencenet.cn/blog-84432-402021.html 此文来自科学网戴越博客，转载请注明出处。
上一篇：Weinberg量子场论书摘及笔记 （2）
下一篇：Weinberg量子场论书摘及笔记 （3）
首先，提供勘误链接，还有Clarifications。这份笔记中也会提到一些勘误。
这本书的书名叫“QFT in a nutshell”，直译过来应是《果壳中的量子场论》。现在有很多书名字都叫《果壳中的……》，据徐教授说，这类名字是他首创的。
场量子化有三种方法：比较常见的（比如说Peskin的书中一开始用到的）是正则量子化方法；本书则从路径积分方法讲起。（还有种方法我忘了。）I.2回顾了量子力学中的路径积分方法。
高斯积分
路径积分方法中经常要用到的数学运算：高斯积分，收录在Appendix 1中。其中出现的重要概念是Wick contraction，在P13的最后。求
的平均值，得到的结果是，这个结果可以理解成6个两两收缩，并对所有可能的收缩求和（后文中出现的即表示这个求和）后得到的结果。每两个收缩得到的结果是，共有三对，即。可能的收缩方式有种，于是就得到。P15的Eq. (16)是Eq. (10)的推广，Eq. (18)是一个具体例子。在这里，Eq. (18)的意义是求矢量的4个分量的乘积的平均值，这样的说法比较难理解。实际上，这样的运算是用来求格林函数的。比如P47的Eq. (10)，如果令，得到的自由传播的四点格林函数形式和P15的Eq. (18)一致，其物理意义是两个粒子传播的几率幅：等号右边第一项表示粒子1从坐标传播到坐标的几率幅（等于），乘以粒子2从坐标传播到坐标的几率幅。由于粒子的全同性，粒子1的末坐标也可能是，于是粒子2从坐标传播到坐标。另外还有第三种可能。把三种情况相加，就得到了两个粒子传播的总几率幅。量子力学中的路径积分
量子力学中，粒子在两点间的运动没有确定的轨道。对于“没有确定的轨道”，一般人就直接理解成“没有轨道”了，而Feynman独辟蹊径，理解成“有许多条（事实上，是无限条）轨道”。路径积分的思想是：对于从一点运动到另一点的任意一条轨道（用
描述粒子运动的轨道），可以用算出这条轨道的几率幅。其中是作用量。粒子在两点间运动的总几率幅就是所有可能的轨道的几率幅之和。在经典极限下，与相比是巨大的，路径的微小改变会造成几率幅的剧烈振荡，使得临近路径的总几率幅会相互抵消掉。只有在取极值的路径附近几率幅不能抵消，这就是可以通过最小作用量原理求出的经典路径。量子场论中的路径积分
量子力学中的研究对象是粒子，用坐标
描述，量子场论中的研究对象则是场。所谓“场”，其实是一个数学概念。给定一个流形...或者不用“流形”这样的名词，我们生活的这个宇宙，每一点都可以用时间-空间四维坐标来描述。在每一个时空点之上都给定一个数，就得到了一个标量场。（也可以在每一点上给定一个矢量，得到矢量场；还可以得到张量场等等。）当然，在场论中研究的场，都是一些有物理意义的动力学函数。给定一个场
，对不同的，不同，对时间的偏导数是场的动能；对空间的不同点，也不同，在场论中，对空间坐标的偏导数是场的动能。（其实应该是场的动量。但动能和动量实际上是同一四维矢量的分量。）总之，场的动能源于场在时空中的“变化”。除此之外，场自身也有相互作用，称为势能。比较重要的势能项，有，其大小和场的平方成正比，系数表征这项作用的强弱。这项势能是场因为自身存在即具有的能量。因为能量即质量，可见其实就是我们熟悉的[静止]质量。还有一个重要的势能项是和成正比的。玻色气体中，每两个气体原子之间具有相互作用，假设相互作用能量是。对于有个原子的玻色气体，总相互作用能量就是，很大时约等于。考虑到，玻色气体原子之间的相互作用其实就是相互作用。知道了场的动能和势能，就能写出拉格朗日量以及作用量，即P17的Eq. (5)。同样，可以算出这个场的几率幅。量子场论中的路径积分方法是：认为所有的场函数
都是可能出现的，计算出所有的几率幅，把它们相加，得到一个总几率幅。和量子力学中类似，如果
做微小变化，一般来说，会导致几率幅的剧烈振荡，使得“相邻”的贡献的几率幅会相互抵消——除非在作用量取极值处。因此，在场论中，同样可以用最小作用量原理，求出“实际出现的”场。对于标量场，这个“实际出现的”场满足Klein-Gordon方程。源对场的作用
后文开始，保持和书上用的记号一致，用
代替。如P20所述。源
会和场耦合，使得场和无源时不同。其原因在于源与场的耦合会改变场的能量，（比如说真空中放入一个电子，就会改变电磁场的能量，）从而改变场的几率幅。作用量取极值的场也会相应地变化。这里有个观念上的变化。初次接触场，应该是中学里学到的电磁场。那时候，场被描述为源“产生”的东西，比如说电荷产生电场，电流产生磁场等。而按场论的观点，电荷和电场，一个是spin-1/2 Dirac场，一个是spin-1 电磁场，完全是两样东西。电荷并不会产生电场，而是因为和电场耦合，从而改变了电场——把电磁场从我们称之为“真空”的状态（这种状态我们以前认为是“没有场”的状态）变成另一种状态。
Wick转动
P12提到了Wick转动，是对时间轴做一个
的变换，其目的是把度规从闵氏的变成欧氏的，这样，在做积分时，可以“平等地”对待四个坐标，从而简化积分运算。有个需要注意的地方：变换不能是，尽管这个变换也能达到同样的目的。其中的原因可以参考P23的Eq. (22)：积分项的奇点在复平面的第二、四象限，Wick转动要避开奇点，因此只能是。 http://blog.sciencenet.cn/blog-84432-402021.html 此文来自科学网戴越博客，转载请注明出处。
上一篇：Weinberg量子场论书摘及笔记 （2）
下一篇：Weinberg量子场论书摘及笔记 （3）
3 支海朝 刘全慧 liangjj
博文
《数理同源》-9-费曼的路径积分（二） 
精选
||
8. 费曼的路径积分（二）
不过，现在还有一个问题：上一节的推导过程是对时间间隔（t2-t1）趋于无限小的时候才能成立，如果对有限长的一段时间（t- t0）又该怎么办呢？费曼对此日思夜想，终于有一天（从梦中醒来后）感觉自己想通了：只需要将整个有限时间段分成很多很多个小时间段，对每一段都可以应用以上同样的做法。然后再令这些时间小段趋于零，而小段的数目趋于无穷大，加起来后求极限。最后，也同样能够在有限的时间区域中导出薛定谔方程【1】。
以经典拉格朗日量作为相位的传播子可以推导出薛定谔方程的这个事实，说明这种方法与薛定谔方程是等价的。所以现在，我们有了三种方法来描述量子力学：除了薛定谔的微分方程、海森堡的矩阵力学之外，又有了费曼的方法！这三种表述都能得到同样的波函数，然而，费曼这种方法到底是什么意思呢？如果按照费曼所想的办法，将有限的时间段分成无限多个小时间段，听起来倒也不是什么新花样，那不就是微积分的思想吗。不过，从上一节的叙述中可知，每一个时间小段的传播子，都包含了一个积分表达式。现在如果有无限多个小时间段的话，总的传播子就应该要做无限多次积分。那么，这无限多次积分的几何图像是什么呢？让我们从以上描述的费曼的思路过程来理解它。
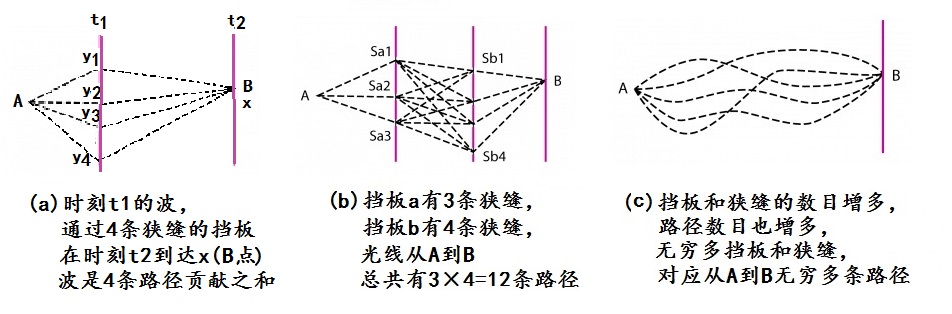
图2：从假想而设立的挡板来理解费曼路径积分
首先，我们考虑从A传播到B的粒子的几率波。如图2a所示，假设粒子传播的过程中，在t1时刻被一个有4条狭缝的挡板挡住了。如果（t2-t1）很小的话，那么，近似而言，这个粒子在t2时刻到达B点的几率是狭缝到B的4条直线路径的贡献之和。如果狭缝数增多，直线路径便增多，各条直线路径对几率的贡献也就相应地叠加上去。关键之点是：狭缝增加到无限多，实际上意味着没有了挡板！因而，没有挡板的情形下，t2时刻到达B点的几率是从t1时刻无限多个不同的位置连到B点的无限多条直线路径的贡献之和。现在，假设A和B之间的时间间隔不是“很小”，那么，的确和微积分的思想一样，现代数学的高招就是将这一段“有限”的时间间隔分成许多许多小间隔，然后对每一个小时间段都运用刚才的方法做一遍。比如说，我们考虑图2b有两个挡板的情形。第一个挡板有3条狭缝，第二个挡板有4条狭缝，那么这时候，这个粒子从A到B的几率是3*4=12条折线路径之和。换个说法，也就是两次求和之乘积。然后，沿用刚才的办法过渡到除去挡板的情形，也就是说，没有挡板的情形下，粒子从A到B的几率是中间两个时刻点无限多个不同的位置连到B点的无限多条“折线”路径的贡献之总和，或称之为二重积分。
再将上面的思路过程推广到A和B之间有n个时间点，即有n个挡板的情形。想象对每个挡板都将以上过程做一遍，然后便不难得出如下结论：粒子从A到B的几率是中间n个时刻点对应的无限多个不同的位置分别连到B点的无限多条“折线”路径的贡献之总和。或者说，是n次无限求和（即积分）之乘积。
再进一步，将时间间隔划分成无限多个时间点，如图2c所示，即令n趋于无穷。这时候，粒子从A到B的几率应该是无限多个积分之乘积。而上述解释过程中所谓的“折线”，也都变成了连续曲线，换言之，这无限多条曲线实际上就是代表了从A到B的所有任意形状的“路径”。
因此，可以将刚才的解释表达得更容易理解一些：从A到B的传播子，或转换函数，是从A到B的所有路径贡献之和。还可以引申成更为数学的语言：这儿的无限多重积分，可以看作是对所有路径的积分，换言之，对“路径空间”的积分。这个路径空间又是什么呢？是所有从A到B的三维曲线构成的空间，这就又回到了我们在本系列最开始介绍伯努利的变分法，即“最速降线问题”时候的那个泛函空间。如此一来，貌似高深的量子力学路径积分与那个简单的几何问题又联系起来了。
后来，费曼企图将这个作法应用到狄拉克的相对论性量子理论时，碰到了困难。再后来，费曼参加到原子弹研究的曼哈顿计划中，无暇顾及这个理论问题。不过他在1942年以此思想为基础完成了他的博士论文“量子力学中的最小作用原理”。大战之后，费曼受聘于康乃尔大学，继续他对量子理论问题的探讨。几年之后，费曼在他的博士论文的基础之上，完善了作用量量子化的路径积分方法。他1948年在《现代物理评论》上发表的“非相对论量子力学的空一时描
写”便是其划时代的代表作。几乎同时，费曼也成功地解决了量子电动力学中的重整化问题，创造出了著名的费曼图和费曼规则，用以方便快捷地近似计算粒子和光子相互作用问题。之后在60年代，费曼又发展了量子场论中的泛函积分方法，其实就是将单粒子的三维函数路径空间推广到场论的多维（无限维）路径空间而已，不过此是后话不表【2】。
费曼的路径积分是“最小作用量原理”在量子力学中的推广。它让我们完全从另外一个角度来理解爱因斯坦的问题：大自然是如何创造这个世界的？科学家们只能从自身的经验和人脑的思维想象来“揣摩”大自然的所谓“意图”。这里涉及到诸多的物理量之中，“哪些是最基本的？”这一类问题。比如说，物理学家最早发现了“力”的概念，后来又有了“能量”的概念。如果有孩子问你：“苹果为什么会掉下来，正好打到牛顿的头上呢？”你起码可以有两种方式回答这个问题。一种方式是从力的观点。你说：“苹果受到地球重力的吸引而下落，我们周围的空间中重力场无处不在，它作用到苹果上，使得苹果在每一个时空点都因为它受到的力而作相应的运动！”。另一种方式呢，你可以从能量的观点来回答：“苹果只有处于势能最低的位置才稳定。所以嘛，它就往下掉，往下掉，一直掉到势能最低无法再低的位置为止！”用更数学的观点来看待这两种说法，第一种是与力场的微分方程有关；第二种方法则是将“能量”视为更为基本的物理量；从前面几节中我们了解了最小作用量原理，所以，你还可以用“作用量”替代“能量”，用第三种说法来解释。也许用作用量来解释苹果的下落不是很直观，那么，我们在上一节中所举的光线、救援者、蚂蚁的行为，便为你提供了很好的实例。
回到理论物理。三个物理量中，力、能量、作用量，到底哪一个更为基本呢？当费曼刚开始提出量子力学的路径积分表述方法时，并未得到主流物理学家的赞同。波尔就是对此长期持反对态度的人之一。波尔实际上非常看重费曼的才华和直率的性格，费曼自己曾经讲过一个故事：按照费曼的说法，费曼刚加入曼哈顿计划时的波尔就如同物理界的神一般受到大家的尊敬。当时，尼尔·波耳任曼哈顿计划的顾问，和他的儿子一起多次到美国洛斯阿拉莫斯实验室访问。费曼如此生动地描述过波尔到来时的两次物理聚会【3】：
“第一次聚会时，我坐在后面的某个角落，只能在众多脑袋瓜的缝隙间看到一点点波耳的影子。但他第二次来开会的那天早上，我接到一个电话。是波尔的儿子打来的，说他父亲想和我谈谈。于是，我和波尔在一个办公室里反复讨论和争论了很久有关原子弹的很多想法。后来我才从小波尔那儿知道了事情的来由：原来上次他们来访后，老波耳跟他儿子说：‘记得坐在后面那小伙子的名字吗？他是这儿唯一一个不怕我的人，只有他会指出我的想法的荒谬。’因此，老波尔决定，下次要讨论什么问题时，不能只找那些只会说‘是，波耳博士！’的人谈话，于是，才在会议之前，先找了我这个‘小人物’去讨论了半天……”
但玻尔对费曼路径积分方法有所误解，还曾经把费曼图误解成粒子运动的轨迹，并对之进行了严厉的批评。没有明确的记载说明爱因斯坦是如何看待路径积分的。费曼和爱因斯坦接触很少，只有过3次短暂的见面。第一次是在普林斯顿大学物理系，1940年末，惠勒建议费曼在魏格纳教授负责的讨论会上报告他们的工作，魏格纳认为惠勒和费曼的工作很重要，他邀请了好几个重量级的大师：天文系的亨利·诺里斯教授、数学系的冯·诺伊曼、当时从苏黎世来访的泡利，当然还特别邀请了大名鼎鼎的爱因斯坦。当时，挑剔的泡利坐在爱因斯坦旁边，自己表示不认可惠勒和费曼的作法，并且询问爱因斯坦的看法，爱因斯坦含糊而温和地答了一句“no”。不过，那时候费曼有关路径积分的思想尚未成熟，报告中讲的主要是有关辐射阻尼的问题。后来，大约是1948年，惠勒曾经将费曼量子力学路径积分的论文交给爱因斯坦看，并对爱因斯坦说：“这个工作不错，对吧？”又问爱因斯坦：“现在，你该相信量子论的正确性了吧！”爱因斯坦也并未直接对费曼文章发表看法，而是沉思了好一会儿，脸色有些灰暗，怏怏不快地说：“也许我有些什么地方弄错了。不过，我仍旧不相信老头子（上帝）会掷骰子！”
六十年代之后，费曼通过他自身人格的魅力、风趣迷人的讲演风格、以及深入浅出的物理论著，使得路径积分的观点对年轻一代物理学家产生了巨大的影响，也逐渐得到老一代前辈的认可。
到七十年代，海森堡和狄拉克都转而相信，量子力学的基本特征是用以解释路径积分的带相位的几率幅，而不是非对易关系。
费曼则在《量子力学与路径积分》这本著作中说：“量子力学中的几率概念并没有改变”、
“所改变了的，并且根本地改变了的，是计算几率的方法。”因此，费曼对量子力学的观点，是基本属于统计诠释一派，只不过，他不是用解微分方程的方法，而是用路径积分的方法来计算几率而已。
微分方程是局域的、立足于力的概念，积分的方法是整体的、基于能量或作用量。这是看问题的两个不同角度，从力的角度看，能量为次级属性。如果从能量或作用量的角度看，力就是一个次级属性。费曼的路径积分使我们从另一个角度来理解量子力学。还不仅仅如此，有时候，更为基本的物理量的正确选择是具有物理意义的，比如AB（阿哈罗诺夫-波姆）效应便是一例。在此我们不再重复叙述，有兴趣者请参考笔者的另一篇博文【4】。
图3：经典到量子
根据路径积分法，从一个时空点（A,tA）到另一个时空点（B, tB）的几率幅，来自于所有可能路径的贡献，每一条路径的贡献的幅度一样，只有相位不同，而其相位则与经典作用量有关，等于（S/ℏ）。
在这儿ℏ是普朗克常数。因此，ℏ正好具有作用量的量纲，可以把它看作是作用量的量子，而S/ℏ表明了对应于每条路径的作用量S的量子化。换言之，路径的作用量子的数目决定了该路径对几率幅的贡献。
更为奇妙的是，路径积分在经典物理和量子物理之间架起了一座桥樑。对宏观尺度来说，作用量子ℏ是个很小很小的量，因此，对每条路线，S 都比ℏ大很多，对该路线的临近路径而言，相位的变化非常巨大而使得这些路径贡献的几率幅相互叠加互相抵消。但有一条路径附近的几率幅不会完全抵消。那就是当这条路径与其临近路线的相位变化不大基本上相同的那条路径，换句话说，也就是对相位的变分为0的那条路径，或者说是作用量S的变分为0的路径。说到这儿，我们已经知道了，那就是经典粒子的路径！如此而来，宏观而言，量子现象就过渡到了经典的运动轨迹，这也就是最小作用量原理与量子力学路径积分之间更深一层的关系。
参考资料：
【1】TheDevelopment of the Space-Time View of Quantum Electrodynamics，NobelLecture by Richard P. Feynman, December 11, 1965。
【2】GENIUSThe Life and Science of Richard Feynman. By James Gleick. New York: Pantheon Books.
【3】《别闹了，费曼先生》，R.费曼，生活·读书·新知三联书店，1997。
【4】《硅火燎原》-28-AB效应和贝里几何相。
http://blog.sciencenet.cn/blog-677221-796611.html 此文来自科学网张天蓉博客，转载请注明出处。
上一篇：《数理同源》-8-费曼的路径积分（一）
下一篇：《数理同源2》-广义相对论与黎曼几何-1
27 王云龙 李笑月 李泳 康娴 陈昌晔 刘建彬 文克玲 薛加民 田云川 罗会仟 李伟钢 徐晓 王喜军 罗德海 高召顺 赵振华 秦伟 钱大鹏 贠可力 jiareng Allanmu wolfganger ychengwei johnnashzhang liyouxi vivikzw lengyonggang
该博文允许注册用户评论 请点击登录 评论 (11 个评论)
- [11]nanyanglds
- [3]薛加民 2014-5-22 11:29 在计算费曼路径积分时，不知对于那些超光速才能走过的路径，是否也要考虑进来？
同此问，路径积分是从负无穷大到正无穷大，考虑到相对论，任何物质的运动都不能超越光速，积分区间是否要进行限制？
- [10]fangfeng1979
- 关于“最小作用量”，还是喜欢莱布尼茨的原版文章。
当然，最早的来源应该是《几何原本》中的这两个定义：
15. 圆：由一条线包围着的平面图形，其内有一点与这条线上任何一个点所连成的线段都相等。
16. 这个点（指定义15中提到的那个点）叫做圆心。
- [9]李维纲
- 更为奇妙的是，路径积分在经典物理和量子物理之间架起了一座桥樑。对宏观尺度来说，作用量子ℏ是个很小很小的量，因此，对每条路线，S 都比ℏ大很多，对该路线的临近路径而言，相位的变化非常巨大而使得这些路径贡献的几率幅相互叠加互相抵消。但有一条路径附近的几率幅不会完全抵消。那就是当这条路径与其临近路线的相位变化不大基本上相同的那条路径，换句话说，也就是对相位的变分为0的那条路径，或者说是作用量S的变分为0的路径。说到这儿，我们已经知道了，那就是经典粒子的路径！如此而来，宏观而言，量子现象就过渡到了经典的运动轨迹，这也就是最小作用量原理与量子力学路径积分之间更深一层的关系。
————————————————————————————————————————————————
如此说来，当氩气分子进入狭管之后，受狭管约束，大体只能沿狭管中轴线做一维运动的情况下，分子的运动路径，无论从经典力学理解，还是从量子力学理解，将没有区别了？这个问题很重要，希望张天蓉博主不吝赐教。
- [8]赵振华
- 写的真好，学习了！
- [7]chc123456
- 老师，还有第五种方法呢
- [6]Zjinney
- 好，同意二楼。
- [5]wolfganger
- 【图2：从假想而设立的挡板来理解费曼路径积分】
这个假设的状态在天上的云彩里比比皆是，宗教在N年前就很清楚。 这些自然的现象用数学物理的方式方法表达出来也就产生了【科学】。【 经典到量子的过程】同理，在南北极的极端云层中 直线 占据绝对的位置，将直线放大，其内部就是【玄之又玄】的多条曲线。 这些都可以在Google earth上看到，我以前曾经给出过观看的具体的方式方法，谁感兴趣可以加QQ：419747187，两分钟即可学会。
文老师，站到南北极的天上，一览纵山小！
- [4]Allanmu
- 张先生辛苦,先赞后看.
- [3]薛加民
- 在计算费曼路径积分时，不知对于那些超光速才能走过的路径，是否也要考虑进来？
- [2]刘建彬
- 费曼的路径积分是“最小作用量原理”在量子力学中的推广。
---
我记得在费曼的某本书上看过，说叫极值定理比较好，我当时理解的是因为只是要求一阶导数等于零，可以是极大，也可以是极小。所以在某些情况下，路径会是最长的那个。
不知道自己理解的的准不准确~
- [1]文克玲
- 曲高和寡。
1/1 | 总计:11 | 首页 | 上一页 | 下一页 | 末页 | 跳转
|
全部作者的精选博文
- • 希尔伯特旅馆悖论
- • 宇宙学中的超光速
- • 光线为什么红移？
- • 佯谬-2-夜空为什么黑暗？
- • 悖论佯谬知多少？
- • 科学思想3-盲人摸象
全部作者的其他最新博文
- • 希尔伯特旅馆悖论
- • 宇宙学中的超光速
- • 光线为什么红移？
- • 佯谬-2-夜空为什么黑暗？
- • 悖论佯谬知多少？
- • 科学思想3-盲人摸象
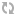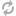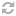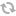
No comments:
Post a Comment