http://quantivity.wordpress.com/2011/02/21/why-log-returns/
human mathematics permalink
August 23, 2011 11:48 am
Regarding the paper links: There is no perfect objective metric. Log returns assumes that investors hate variance per se, whereas in fact investors hate drawdowns. Investors also hate some integral of drawdowns convolved with a convex function of time. Unless they subscribe to some philosophy, e.g. buy-and-hold-and-never-let-go, that has taught them otherwise.[DOC]
误差理论与数据处理 - 湖北省教育考试院
www.hbea.edu.cn/files/.../06018误差理论与数据处理.doc
轉為繁體網頁
每個數值樣本 先平方一次再全部加總起來求平均值
: 得到了數值樣本的平均值後再開根號
以振幅來說 平均應該是0(因為有方向性抵銷的關係), : 方均根看到的則是振幅波動的大小(但是看不到方向)
: 方均根看到的則是振幅波動的大小(但是看不到方向)
0Comment count
|
1View count
|
8/10/14
| |||||
0Comment count
|
1View count
|
8/10/14
| |||||
逢甲大學統計與精算研究所碩士論文 - 逢甲大學學位論文提交 ...
ethesys.lib.fcu.edu.tw/ETD-search/getfile?URN=etd-0222110...etd...
μ (對數常態模型) ....................... 177. 表8-4-13 不同殘差下之預測標準誤的變化率(
Logarithmic growth
From Wikipedia, the free encyclopedia
A familiar example of logarithmic growth is the number of digits needed to represent a number, N, in positional notation, which grows as logb (N), where b is the base of the number system used, e.g. 10 for decimal arithmetic.[3] In more advanced mathematics, the partial sums of the harmonic series
Logarithmic growth can lead to apparent paradoxes, as in the martingale roulette system, where the potential winnings before bankruptcy grow as the logarithm of the gambler's bankroll.[5] It also plays a role in the St. Petersburg paradox.[6]
In microbiology, the rapidly growing exponential growth phase of a cell culture is sometimes called logarithmic growth. During this bacterial growth phase, the number of new cells appearing are proportional to the population. This terminological confusion between logarithmic growth and exponential growth may possibly be explained by the fact that exponential growth curves may be straightened by plotting them using a logarithmic scale for the growth axis.[7]
Uncommon Returns through Quantitative and Algorithmic Trading
Why Log Returns
February 21, 2011
A reader recently asked an important question, one which often puzzles those new to quantitative finance (especially those coming from technical analysis, which relies upon price pattern analysis):
Begin by defining a return: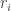
at time 
, where 
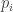is the price at time and 
:
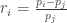
Benefit of using returns, versus prices, is normalization: measuring all variables in a comparable metric, thus enabling evaluation of analytic relationships amongst two or more variables despite originating from price series of unequal values. This is a requirement for many multidimensional statistical analysis and machine learning techniques. For example, interpreting an equity covariance matrix is made sane when the variables are both measured in percentage.
Several benefits of using log returns, both theoretic and algorithmic.
First, log-normality: if we assume that prices are distributed log normally (which, in practice, may or may not be true for any given price series), then
is conveniently normally distributed, because:
This is handy given much of classic statistics presumes normality.
Second, approximate raw-log equality: when returns are very small (common for trades with short holding durations), the following approximation ensures they are close in value to raw returns:
, 
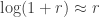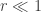
Third, time-additivity: consider an ordered sequence of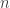
trades. A statistic frequently calculated from this sequence is the compounding return, which is the running return of this sequence of trades over time:
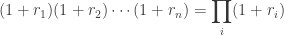
This formula is fairly unpleasant, as probability theory reminds us the product of normally-distributed variables is not normal. Instead, the sum of normally-distributed variables is normal (important technicality: only when all variables are uncorrelated), which is useful when we recall the following logarithmic identity:
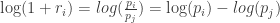
Thus, compounding returns are normally distributed. Finally, this identity leads us to a pleasant algorithmic benefit; a simple formula for calculating compound returns:
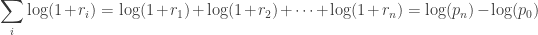
Thus, the compound return over n periods is merely the difference in log between initial and final periods. In terms of algorithmic complexity, this simplification reduces O(n) multiplications to O(1) additions. This is a huge win for moderate to large n. Further, this sum is useful for cases in which returns diverge from normal, as the central limit theorem reminds us that the sample average of this sum will converge to normality (presuming finite first and second moments).
Fourth, mathematical ease: from calculus, we are reminded (ignoring the constant of integration):
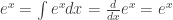
This identity is tremendously useful, as much of financial mathematics is built upon continuous time stochastic processes which rely heavily upon integration and differentiation.
Fifth, numerical stability: addition of small numbers is numerically safe, while multiplying small numbers is not as it is subject to arithmetic underflow. For many interesting problems, this is a serious potential problem. To solve this, either the algorithm must be modified to be numerically robust or it can be transformed into a numerically safe summation via logs.
As suggested by John Hall, there are downsides to using log returns. Here are two recent papers to consider (along with their references):
Why use the logarithm of returns, rather than price or raw returns?The answer is several fold, each of whose individual importance varies by problem domain.
Begin by defining a return:
at time , where is the price at time and :Benefit of using returns, versus prices, is normalization: measuring all variables in a comparable metric, thus enabling evaluation of analytic relationships amongst two or more variables despite originating from price series of unequal values. This is a requirement for many multidimensional statistical analysis and machine learning techniques. For example, interpreting an equity covariance matrix is made sane when the variables are both measured in percentage.
Several benefits of using log returns, both theoretic and algorithmic.
First, log-normality: if we assume that prices are distributed log normally (which, in practice, may or may not be true for any given price series), then
is conveniently normally distributed, because:This is handy given much of classic statistics presumes normality.
Second, approximate raw-log equality: when returns are very small (common for trades with short holding durations), the following approximation ensures they are close in value to raw returns:
, Third, time-additivity: consider an ordered sequence of
trades. A statistic frequently calculated from this sequence is the compounding return, which is the running return of this sequence of trades over time:This formula is fairly unpleasant, as probability theory reminds us the product of normally-distributed variables is not normal. Instead, the sum of normally-distributed variables is normal (important technicality: only when all variables are uncorrelated), which is useful when we recall the following logarithmic identity:
Thus, compounding returns are normally distributed. Finally, this identity leads us to a pleasant algorithmic benefit; a simple formula for calculating compound returns:
Thus, the compound return over n periods is merely the difference in log between initial and final periods. In terms of algorithmic complexity, this simplification reduces O(n) multiplications to O(1) additions. This is a huge win for moderate to large n. Further, this sum is useful for cases in which returns diverge from normal, as the central limit theorem reminds us that the sample average of this sum will converge to normality (presuming finite first and second moments).
Fourth, mathematical ease: from calculus, we are reminded (ignoring the constant of integration):
This identity is tremendously useful, as much of financial mathematics is built upon continuous time stochastic processes which rely heavily upon integration and differentiation.
Fifth, numerical stability: addition of small numbers is numerically safe, while multiplying small numbers is not as it is subject to arithmetic underflow. For many interesting problems, this is a serious potential problem. To solve this, either the algorithm must be modified to be numerically robust or it can be transformed into a numerically safe summation via logs.
As suggested by John Hall, there are downsides to using log returns. Here are two recent papers to consider (along with their references):
- Comparing Security Returns is Harder than You Think: Problems with Logarithmic Returns, by Hudson (2010)
- Quant Nugget 2: Linear vs. Compounded Returns – Common Pitfalls in Portfolio Management, by Meucci (2010)
30 Comments leave one →
Trackbacks
- Finanzas 101: Calculos con Retornos « Quantitative Finance Club
- Why Minimize Negative Log Likelihood? « Quantivity
- Why log returns? « mathbabe
- Geometric Efficient Frontier « Systematic Investor
- Pathetic Model Using VIX To Predict S&P 500, Part 1 | Curated Alpha
- Links 30 Mar « Pink Iguana
- franziss | Pearltrees
- Pair Trading Model « ickyatcity
- Learning Algorithmic Trading | Bordering Insanity
- Misleading Elvish Statistics | Chen's blog
- Why log returns ? |
- Why Use Log Returns? | Châteaux de Bah
In my own study, I was convinced most by the explanation in Meucci’s Risk and Asset Allocation book. There are hints of what he says in what you say. Basically, his argument is that you should take some invariants and then map them to expected market prices. Since you should be concerned about how these invariants move forward into time and how they can be combined into market prices, the properties of the invariants are more important than the properties of the final market prices (arithmetic returns are easy to aggregate for 1 point in time, but geometric returns are better to aggregate through time). Also, as you note, there is an easy formula to convert one to the other.
I was a bit tripped up in his analysis b/c if the geometric returns follow some garch or regime-switching process, then they aren’t IID. However, the log returns of these variables can still be projected in each period following these processes and then mapped to market prices for use in optimization. Meucci has a good short paper on why you shouldn’t use the projection of log returns in optimization on ssrn.
It might be even more complicated than downsides — maybe brief upsides vs spiky upsides vs long-and-steady affects how investors take the downside. I’m reading The Big Short right now. It’s incredible how Michael Burry’s investors lampooned him, even when he was RIGHT, calling the biggest short of the last decade with surgical precision. http://books.google.com/books?id=eParwQ0YdrcC&printsec=frontcover&dq=the+big+short&hl=en&src=bmrr&ei=vQ9VTpCDN8K_tgfDl_CPAg&sa=X&oi=book_result&ct=book-thumbnail&resnum=1&ved=0CEIQ6wEwAA#v=onepage&q=his%20investors&f=false
Sure – you have my email now – so beep at me when you’ve finished it.
‘X’ amount of profit is a quantity in a 10-digit space,which gives a distorted view of natural quantities. One has to take the natural logarithm of a naturally occured quantity to bring it down to the undistorted /real scale. This is why it is called ‘Natural’ Logarithm. Hence, we takke the natural logiartihm of the returns to apply summation and substraction operations on them.
This is also why , the ln() of the returns has a normal distribution..This is also why, linear interpolation works on the ln() of the returns.
Why dont you write $\log(r_n) – \log(r_0)$ instead?
want. There need to be more things like this on WordPress
Have a related question and maybe you can provide guidance.
You said:
“… if we assume that prices are distributed log normally (which, in practice, may or may not be true for any given price series)”
“… given much of classic statistics presumes normality”
Question: How material is the “normality assumption” in creating profitable quant models and strategies?
How can one discern when this assumption is realistic (worth working with as a practitioner) and when is it purely for academical reasons?
Allow me to elaborate based on my limited knowledge so far.
It seems that the vast majority of quantitative education is founded on the normality assumption and on the creation of models from historical distributions.
“Risk” seems to be about going (or not going) outside the first/second standard deviation of the Gaussian curve.
As a trader, it almost sounds like this was born in a “buy and hold” world where time works in an investor`s favor.
Also as a trader, I know that outside the first standard deviations is where the best trades are in this volatile world.
On the other hand (from the Gaussian assumption), quant practitioners like Nassim Taleb advocate for non Gaussian ways.
Some highlights below:
“Granted, it has been tinkered with, using such methods as complementary “jumps”, stress testing, regime switching or the elaborate methods known as GARCH, but while they represent a good effort, they fail to address the bell curve’s fundamental flaws.
…
These two models correspond to two mutually exclusive types of randomness: mild or Gaussian on the one hand, and wild, fractal or “scalable power laws” on the other. Measurements that exhibit mild randomness are suitable for treatment by the bell curve or Gaussian models, whereas those that are susceptible to wild randomness can only be expressed accurately using a fractal scale. The good news, especially for practitioners, is that the fractal model is both intuitively and computationally simpler than the Gaussian, which makes us wonder why it was not implemented before.
…
Indeed, this fractal approach can prove to be an extremely robust method to identify a portfolio’s vulnerability to severe risks. Traditional “stress testing” is usually done by selecting an arbitrary number of “worst-case scenarios” from past data. It assumes that whenever one has seen in the past a large move of, say, 10 per cent, one can conclude that a fluctuation of this magnitude would be the worst one can expect for the future. This method forgets that crashes happen without antecedents. Before the crash of 1987, stress testing would not have allowed for a 22 per cent move.
…
Any attempts to refine the tools of modern portfolio theory by relaxing the bell curve assumptions, or by “fudging” and adding the occasional “jumps” will not be sufficient. We live in a world primarily driven by random jumps, and tools designed for random walks address the wrong problem. It would be like tinkering with models of gases in an attempt to characterise them as solids and call them “a good approximation”.
Pasted from the “A focus on the exceptions that prove the rule” article on ft dot com.
Like I said at the beginning I am looking for a quant edge and need a way to navigate through the vast knowledge and avoid assumptions that are incompatible with a practitioner`s reality.
Can you please offer some criteria and/or references that would help me navigate?
Is the Gaussian assumption safe as foundation for profitable models?
How to verify this?
In practice, the single most important concept to understand is the existence and distinction between alpha model and risk model; and use of the correct corresponding quantitative methodology for each.
- Alpha model: describes how you make money; use whatever model makes the best money
- Risk model: describes your downside risk exposure; use whatever model best describes reality of the alpha phenomenon
Many folks unknowingly conflate the two. Avoid that.To your specific questions:
Q: How material is the “normality assumption” in creating profitable quant models and strategies?
A: Irrelevant for alpha model; if a model makes money (whatever the distribution), trade it. Maybe relevant for risk model, if alpha phenomenon is best described by a non-Gaussian distribution.
Q: How can one discern when this assumption is realistic (worth working with as a practitioner) and when is it purely for academical reasons?
A: Build and then measure: build a risk model, trade over time, and then measure whether you lose more money than you expect. If you are losing more than your model says, then one of your assumptions is wrong.
Q: Vast majority of quantitative education is founded on the normality assumption and on the creation of models from historical distributions.
A: Historical accident. Gaussian distributions (and exponential distributions, more generally) are mathematically convenient, so much of closed-form Q world is built on them. Modern computational finance and ML methods, such as Monte Carlo methods (e.g. particle filters), are mostly agnostic to distribution assumptions.
Q: Is the Gaussian assumption safe as foundation for profitable models?
A: Maybe or maybe not. Models should be built to describe reality. Blind adherence to any unverified mathematical assumption(s) are likely to lead to hardship in trading.
Q: How to verify this?
A: Many diverse statistical techniques exist. QQ-plot is an elementary technique from exploratory analysis which may be applicable.
Q: Can you please offer some criteria and/or references that would help me navigate?
A: Strive to build models that describe reality. Use the best tools at your disposal and make as few unverified assumptions as possible. Continuously check reality to verify it matches your assumptions.