6. 傅里叶变换有什么用?
摆弄一系列三角函数,让这个多点那个少点,有一个酷炫的名字,叫“频域处理”,
你去了美国,不知道白宫怎么走,你问翻译:白宫怎么走?
翻译跑到街上问美国人:Where is the White House?这叫傅里叶变换。
美国路人说:“go straight and turn right”。这叫频域处理。
翻译听完给你说:直走,右拐就到了。这叫逆傅里叶变换。
总结:傅里叶变换的作用,就是把一个函数或者信号在三角函数基下转化为一堆系数,摆弄这些系数、实现一定功能有时比直接摆弄原信号方便,最后再做个逆傅里叶变换,信号就得到了某种处理。
如何直观形象、生动有趣地给文科学生介绍傅立叶变换?
从数学的角度,提供一个形象有趣的解释。有点啰嗦,如果你愿意,可以修改出一个更加浓缩的版本讲给文科生听。
1. 什么是基?
假设一个科研所有四个所长(一正三副),四个所长各司其职,把整个科研所的事物管理的井井有条。这四个所长,少一个,单位的工作无法顺利展开,多一个碍手碍脚事倍功半,他们四人一道就组成了科研所的一个“基”。
一个单位的基可能不是唯一的,四个人换换位置工作也能展开,调走一个人再换一个人来顶替,单位亦可以正常运转,但是 4 这个数是不能变化的(数学语言:基的维数固定不变)。
总结:一组基,就是足够能描述、表达某类事物的最少的一小撮元素们。
2. 基只有一种形式吗?
我们把科研所的日常事务换成感情,把四个所长换成语言字典重新来叙述。
假设你爱上了一个人,需要向她表达感情。这时就需要一套表达感情的工具——语言。如果使用汉语,你可以说“我爱你”,如果使用英文,你可以说“I love you”。汉语的所有词汇构成了一个集合,英语的所有词汇也构成了一个集合,它们都可以描述感情、感觉、事物和知识,它们是两套不同的描述系统,也分别有自己的基。
总结:描述事物的基可以有很多套。
3. 基有什么特点?
汉语的词汇量很大,有很多重复意义的词,比如我爱你就可以重新表述为:“俺爱你”,“我爱侬”,“我想和你困觉”等等。我们把汉语词汇中所有同意的词只保留一个(数学语言:使线性无关),留下来的词汇量较少的词典就是汉语的一个基,里面的每一个词被称作基函数。它的特点是:所有感情、感觉、事物和知识都可以用从这个较小的词汇本中挑出的一些词汇(基函数)经过精心安排(加权相加)来描述,并且只有一种描述方式(数学语言:若基固定,则对应系数 / 坐标确定),因为我们已经去掉了冗余的、近似的词汇,因此不存在一个事物在一个基下有两种不同表示法存在。
总结:一套基中的元素很多,足够描述事物,只要从中挑出一些你需要的,按某种方式组合在一起即可,一套基中的元素也不能太多,以至于这种描述事物的方法是唯一的。
4. 不同基之间有什么联系?
给定两个不同的语言,给出两个不同语言的小字典(两个基),我们都可以分别用唯一的方式表达感情、感觉、事物和知识。这两种表示法之间可以相互转换(数学语言:坐标变换)。“I love you”和“我爱你”可以相互转化。
总结:给定一个基,我们就可以用这组基表达事物,也可以用它来翻译用其他基描述的事物,不同基下的表示可以相互转换。
5. 什么是傅里叶变换?
大家还记得三角函数 sin 和 cos 吗,就是那种波浪形状的函数,一个波浪的的宽度可以是不同的,既可以像跳大绳一样宽,也可以像电炉丝一样窄(数学语言:频率不同)。把这些三角函数放到一起组成一个字典,就恰好是连续函数的一组基:任何一个连续函数,都可以唯一表示成一群三角函数相叠加。然而每个三角函数的分量有轻有重,相加的时候有的要拉高点,有的要压低点,有的要朝左朝右摆一摆,有的干脆不用(数学语言:加权系数不同)。到底是哪些三角函数呢,各个三角函数的分量如何呢?找到它们的过程,被称为傅里叶变换。
举几个例子:
从下面的几个例子可以看出,把一系列震荡的三角函数按照傅里叶系数(权值)进行缩放和平移再加起来,大概 40 个三角函数加到一起,就和原来的函数长得差不多了,无论原来的那个函数长的有多么奇特。因此我们说:蚂蚁也能撼大树,三角函数多了加到一起,多奇怪的连续函数我长的都能和你是一个样!!
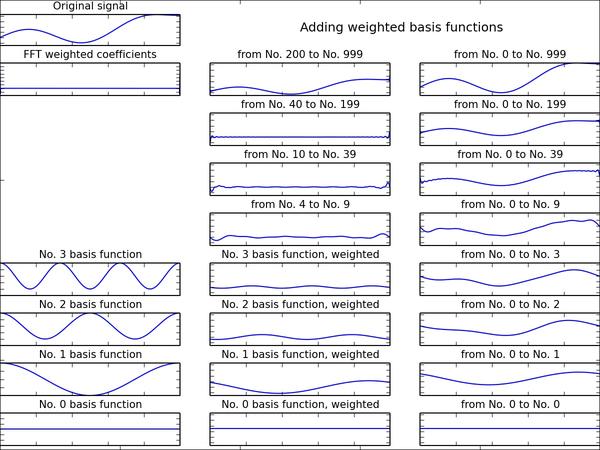
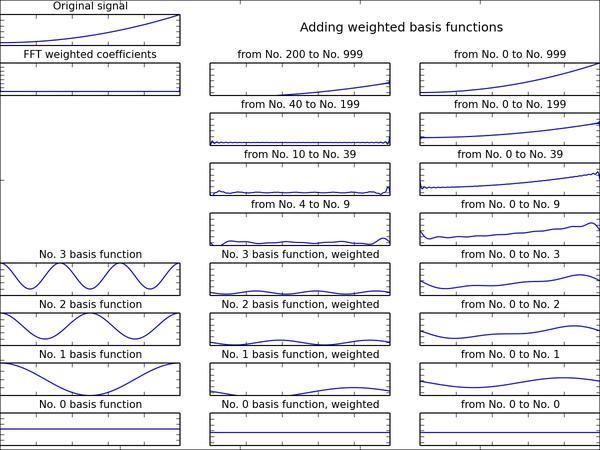
总结:给你一个函数,找到它的傅里叶变换,就是找到一堆系数,每一个系数对应一个不同频率的三角函数,这些三角函数分别按各自的系数进行放缩和平移(数学语言:改变振幅和相位),然后叠加在一起,恰好就与原来那个函数相等。
因此,四个处长是一组基,能维持一个单位的运转,处理各种问题;
一套简化的汉语词典是一组基,什么样的情感它都能找到唯一的表达语句;
一堆三角函数是一组基,什么样的连续函数都可以用一大堆三角函数叠加获得。(不要小看振荡的东西哦,振荡的函数多了,啥都能组合出来。别嫌方块简单,Minecraft 世界你永远也玩不腻!)
6. 傅里叶变换有什么用?
摆弄一系列三角函数,让这个多点那个少点,有一个酷炫的名字,叫“频域处理”,
你去了美国,不知道白宫怎么走,你问翻译:白宫怎么走?
翻译跑到街上问美国人:Where is the White House?这叫傅里叶变换。
美国路人说:“go straight and turn right”。这叫频域处理。
翻译听完给你说:直走,右拐就到了。这叫逆傅里叶变换。
总结:傅里叶变换的作用,就是把一个函数或者信号在三角函数基下转化为一堆系数,摆弄这些系数、实现一定功能有时比直接摆弄原信号方便,最后再做个逆傅里叶变换,信号就得到了某种处理。
7. 频域处理是很玄的东西,如何理解?
如果你不懂英文,一个妙龄少女对你说:Hi. I love you. Are you free tonight? 你会回复她:姑娘你能不能不要说鸟语?滚回美帝玩泥巴吧。
在某些领域,傅里叶变换后的系数非常有用。为了显示方便,举一个二维的例子。见下图:

原始图像中含有噪声,因为噪声往往是细小的雪花点,属于图像高频分量,因此我们把图像首先做傅里叶变换,然后把变换后的三角函数前的系数中属于高频的部分全部去掉(置 0),然后再做逆傅里叶变换,我们发现图像中的细节(噪声点)消失了。这就是频率域去噪的基本原理。
8. 还有哪些基我们可能听过,但是不曾认识到?
多项式基:多项式多了,啥稀奇古怪的函数都能表示,不信你试试泰勒展开式有多好用就知道了。
小波基:傅里叶基(三角函数)的改进,可以进行局部控制。
B- 样条基:多项式基的改进,可以进行局部控制。
一幅 800*600 的图像,我们既可以认为它是一幅抽象的图像,也可以认为它是一个由 800*600 个基函数(一个基函数是某一颗像素值为 1,其他所有像素值为 0 的图像)进行加权相加获得的一个坐标表示。
1. 什么是基?
假设一个科研所有四个所长(一正三副),四个所长各司其职,把整个科研所的事物管理的井井有条。这四个所长,少一个,单位的工作无法顺利展开,多一个碍手碍脚事倍功半,他们四人一道就组成了科研所的一个“基”。
一个单位的基可能不是唯一的,四个人换换位置工作也能展开,调走一个人再换一个人来顶替,单位亦可以正常运转,但是 4 这个数是不能变化的(数学语言:基的维数固定不变)。
总结:一组基,就是足够能描述、表达某类事物的最少的一小撮元素们。
2. 基只有一种形式吗?
我们把科研所的日常事务换成感情,把四个所长换成语言字典重新来叙述。
假设你爱上了一个人,需要向她表达感情。这时就需要一套表达感情的工具——语言。如果使用汉语,你可以说“我爱你”,如果使用英文,你可以说“I love you”。汉语的所有词汇构成了一个集合,英语的所有词汇也构成了一个集合,它们都可以描述感情、感觉、事物和知识,它们是两套不同的描述系统,也分别有自己的基。
总结:描述事物的基可以有很多套。
3. 基有什么特点?
汉语的词汇量很大,有很多重复意义的词,比如我爱你就可以重新表述为:“俺爱你”,“我爱侬”,“我想和你困觉”等等。我们把汉语词汇中所有同意的词只保留一个(数学语言:使线性无关),留下来的词汇量较少的词典就是汉语的一个基,里面的每一个词被称作基函数。它的特点是:所有感情、感觉、事物和知识都可以用从这个较小的词汇本中挑出的一些词汇(基函数)经过精心安排(加权相加)来描述,并且只有一种描述方式(数学语言:若基固定,则对应系数 / 坐标确定),因为我们已经去掉了冗余的、近似的词汇,因此不存在一个事物在一个基下有两种不同表示法存在。
总结:一套基中的元素很多,足够描述事物,只要从中挑出一些你需要的,按某种方式组合在一起即可,一套基中的元素也不能太多,以至于这种描述事物的方法是唯一的。
4. 不同基之间有什么联系?
给定两个不同的语言,给出两个不同语言的小字典(两个基),我们都可以分别用唯一的方式表达感情、感觉、事物和知识。这两种表示法之间可以相互转换(数学语言:坐标变换)。“I love you”和“我爱你”可以相互转化。
总结:给定一个基,我们就可以用这组基表达事物,也可以用它来翻译用其他基描述的事物,不同基下的表示可以相互转换。
5. 什么是傅里叶变换?
大家还记得三角函数 sin 和 cos 吗,就是那种波浪形状的函数,一个波浪的的宽度可以是不同的,既可以像跳大绳一样宽,也可以像电炉丝一样窄(数学语言:频率不同)。把这些三角函数放到一起组成一个字典,就恰好是连续函数的一组基:任何一个连续函数,都可以唯一表示成一群三角函数相叠加。然而每个三角函数的分量有轻有重,相加的时候有的要拉高点,有的要压低点,有的要朝左朝右摆一摆,有的干脆不用(数学语言:加权系数不同)。到底是哪些三角函数呢,各个三角函数的分量如何呢?找到它们的过程,被称为傅里叶变换。
举几个例子:
从下面的几个例子可以看出,把一系列震荡的三角函数按照傅里叶系数(权值)进行缩放和平移再加起来,大概 40 个三角函数加到一起,就和原来的函数长得差不多了,无论原来的那个函数长的有多么奇特。因此我们说:蚂蚁也能撼大树,三角函数多了加到一起,多奇怪的连续函数我长的都能和你是一个样!!


总结:给你一个函数,找到它的傅里叶变换,就是找到一堆系数,每一个系数对应一个不同频率的三角函数,这些三角函数分别按各自的系数进行放缩和平移(数学语言:改变振幅和相位),然后叠加在一起,恰好就与原来那个函数相等。
因此,四个处长是一组基,能维持一个单位的运转,处理各种问题;
一套简化的汉语词典是一组基,什么样的情感它都能找到唯一的表达语句;
一堆三角函数是一组基,什么样的连续函数都可以用一大堆三角函数叠加获得。(不要小看振荡的东西哦,振荡的函数多了,啥都能组合出来。别嫌方块简单,Minecraft 世界你永远也玩不腻!)
6. 傅里叶变换有什么用?
摆弄一系列三角函数,让这个多点那个少点,有一个酷炫的名字,叫“频域处理”,
你去了美国,不知道白宫怎么走,你问翻译:白宫怎么走?
翻译跑到街上问美国人:Where is the White House?这叫傅里叶变换。
美国路人说:“go straight and turn right”。这叫频域处理。
翻译听完给你说:直走,右拐就到了。这叫逆傅里叶变换。
总结:傅里叶变换的作用,就是把一个函数或者信号在三角函数基下转化为一堆系数,摆弄这些系数、实现一定功能有时比直接摆弄原信号方便,最后再做个逆傅里叶变换,信号就得到了某种处理。
7. 频域处理是很玄的东西,如何理解?
如果你不懂英文,一个妙龄少女对你说:Hi. I love you. Are you free tonight? 你会回复她:姑娘你能不能不要说鸟语?滚回美帝玩泥巴吧。
在某些领域,傅里叶变换后的系数非常有用。为了显示方便,举一个二维的例子。见下图:

原始图像中含有噪声,因为噪声往往是细小的雪花点,属于图像高频分量,因此我们把图像首先做傅里叶变换,然后把变换后的三角函数前的系数中属于高频的部分全部去掉(置 0),然后再做逆傅里叶变换,我们发现图像中的细节(噪声点)消失了。这就是频率域去噪的基本原理。
8. 还有哪些基我们可能听过,但是不曾认识到?
多项式基:多项式多了,啥稀奇古怪的函数都能表示,不信你试试泰勒展开式有多好用就知道了。
小波基:傅里叶基(三角函数)的改进,可以进行局部控制。
B- 样条基:多项式基的改进,可以进行局部控制。
一幅 800*600 的图像,我们既可以认为它是一幅抽象的图像,也可以认为它是一个由 800*600 个基函数(一个基函数是某一颗像素值为 1,其他所有像素值为 0 的图像)进行加权相加获得的一个坐标表示。
当你听到我的声音时,你便知道是我来了;
我见到你的面孔;我便知道那就是你「1」:
一切都那么自然,我从未仔细想过其中的道理。
但从你离我远去的一刻起,这个世界全都进入了一个颠倒的空间里「2」。
我不再知道你在哪儿,只知道你离我远去的速度「3」;
我闭上眼睛不愿见到你远去,只听见汽笛声变得渐渐低沉下去「4」;
听不见你的琴声,只有琴谱还留在那里「5」;
将现实的世界,投向另一个空间,望着你在那里的投影「6」。
我多么想知道你的一切,
我在低频的影子里,寻找你身体的轮廓;
我在高频的影子里,寻找你的每个细节。「7」
在 Fourier 的频谱空间里,你永远在这里。
这个东西是前面突然想到写的,下面是一些注释:
「1」对声音的识别和对面孔的识别现在常用的方法也都是通过谱分析的方法进行的;
「2」物理学家(尤其是晶体学家)常常用“倒空间”来说 Fourier 空间,动量空间,例如正空间中的面心立方在倒空间里就是体心立方;
「3」从坐标空间变成了动量(速度,频率)空间,我在这里还想暗示由谱分析的方法所能推导的 Heisenberg 不确定关系的存在;
「4」通过 Doppler 效应,从频率的变化推断物体的运动速度;
「5」对声音的 Fourier 分析,得到振动谱(也正是乐谱);
「6」Fourier 分量等于在 Fourier 空间基矢上的投影;
「7」频谱分析的高频、低频信号的特征。
关于 Fourier 变换,另一个好的文章是《不确定原理的前世今生》,猛烈推荐:
http://songshuhui.net/archives/50111
我见到你的面孔;我便知道那就是你「1」:
一切都那么自然,我从未仔细想过其中的道理。
但从你离我远去的一刻起,这个世界全都进入了一个颠倒的空间里「2」。
我不再知道你在哪儿,只知道你离我远去的速度「3」;
我闭上眼睛不愿见到你远去,只听见汽笛声变得渐渐低沉下去「4」;
听不见你的琴声,只有琴谱还留在那里「5」;
将现实的世界,投向另一个空间,望着你在那里的投影「6」。
我多么想知道你的一切,
我在低频的影子里,寻找你身体的轮廓;
我在高频的影子里,寻找你的每个细节。「7」
在 Fourier 的频谱空间里,你永远在这里。
这个东西是前面突然想到写的,下面是一些注释:
「1」对声音的识别和对面孔的识别现在常用的方法也都是通过谱分析的方法进行的;
「2」物理学家(尤其是晶体学家)常常用“倒空间”来说 Fourier 空间,动量空间,例如正空间中的面心立方在倒空间里就是体心立方;
「3」从坐标空间变成了动量(速度,频率)空间,我在这里还想暗示由谱分析的方法所能推导的 Heisenberg 不确定关系的存在;
「4」通过 Doppler 效应,从频率的变化推断物体的运动速度;
「5」对声音的 Fourier 分析,得到振动谱(也正是乐谱);
「6」Fourier 分量等于在 Fourier 空间基矢上的投影;
「7」频谱分析的高频、低频信号的特征。
关于 Fourier 变换,另一个好的文章是《不确定原理的前世今生》,猛烈推荐:
http://songshuhui.net/archives/50111


No comments:
Post a Comment