散度和旋度的物理意义是什么？
散度和旋度的物理意义, 其他回答都说得很清楚了: 散度, 就是是否有源. 旋度也正是"描述矢量场中某一点所包含微元在场中的旋转程度".
但这里有一个subtle的地方. 有一个答案这么说:
但这里有一个subtle的地方. 有一个答案这么说:
因为科里奥利力的原因，水从孔流出时，水缸里有漩涡，这是旋度
这其实是不对的. 旋度说的是液体微粒的自转(vorticity).
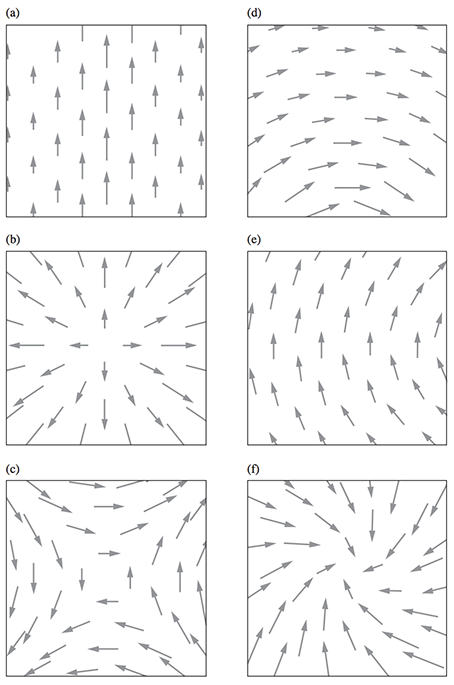
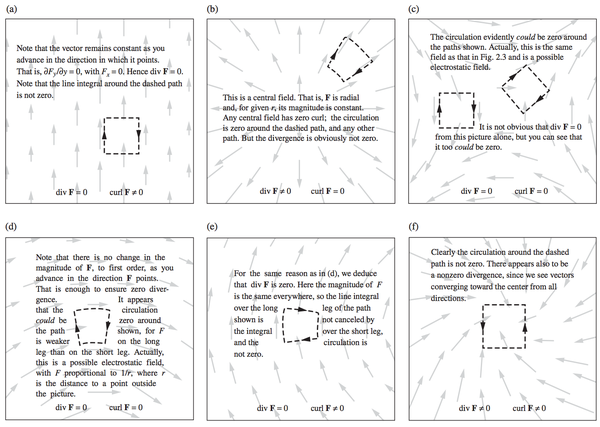
有一个经典的例子: (下图取自Purcell的Electricity and Magnetism的Figure 2.39和2.40)
图中的两个向量场都是无源的, 即散度为零. 但(d)的旋度为零, (e)的旋度不为零. 分析如下:
如(d)中的提示所说, 详细的计算表明:
有一个经典的例子: (下图取自Purcell的Electricity and Magnetism的Figure 2.39和2.40)
图中的两个向量场都是无源的, 即散度为零. 但(d)的旋度为零, (e)的旋度不为零. 分析如下: 如(d)中的提示所说, 详细的计算表明:
- 如果一个流体整体绕其中心轴以角速度
旋转, 则流体速度场的旋度大小处处为
.
- 如果一个流体绕其中心轴旋转, 速度与距中心轴的距离成反比, 则流体速度场的旋度大小处处为零.
有一个回答很小心地指出"假设球心位置不改变", 这是很必要的.
Figure 2.39和2.40对于直观理解散度和旋度的物理意义很有帮助. 下面完整给出, 作为其他回答的补充:
P.S.
水的漩涡也不是由于Coriolis effect引起. 这个效应太微弱了, 不足以在这么小的系统中产生影响. 可以参考: http://songshuhui.net/archives/7126.
电磁场与电磁波第5讲旋度和旋度定理零恒等式亥姆霍兹定理-y
2015年2月16日 - 十四维空间理论证明尝试:首先，我们知道，十维空间是将无穷多种可能性叠加后，
但是，以闭合回路为边界的曲面不是唯一的，原则上有无穷多个。也就是说，在稳恒电流情况下，对于以闭合回路为边界的所有曲面而言，安培环路定理总是成立的。
原本的運動方程式，，代表一個開迴路系統，這個系統的兩個極點，，其阻尼比大約只有，因此的震盪 .... 而要對連續(因此為無窮多)的數據進行運算，更是非常麻煩
高中生没专业学过，出错不负责]
wiki:（我只能看懂这些）
在三维直角坐标系Oxyz中，设向量场
为[2]:8：
，
其中的
分别是x轴、y轴、z轴方向上的单位向量，场的分量P、Q、R具有一阶连续偏导数， 那么在各个坐标上的投影分别为：
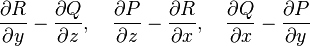的向量叫做向量场A的旋度，也就是[1]:14：
旋度的表达式可以用也行列式记号形式表示[2]:4-5：
需要注意的是这里的行列式记号只有形式上的意义，因为真正的行列式中的系数应该是数而不是这样的向量。这种表示方法只是便于记忆旋度在直角坐标系中的表达式[3]。
感觉已经讲得很清楚了
物理意义：
（斯托克斯定理）当一个向量场的旋度是零时场为保守场，即闭合曲线上F点乘dl积分为零。物理上就是带着物体走一圈场做功为零，如重力场，电场（无磁通量变化）
[0] |
2楼
3楼
4楼
5楼
7楼
8楼
9楼
www.docin.com/p-734619567.html
轉為繁體網頁
2013年12月3日 - ... 注意：在每一点P处都有无穷多的方向旋度d s ˆ s a d l P 回路（回路的绕行方向）与回路包围面（面法线方向）这两个方向之间的关系：右手规则8 J (1) ...
www.docin.com/p-734619567.html
轉為繁體網頁
轉為繁體網頁
电磁场与电磁波第5讲旋度和旋度定理零恒等式亥姆霍兹定理-y
www.docin.com/p-734619567.html
轉為繁體網頁
2013年12月3日 - 若环量不等于零，说明闭合曲线内存在有旋源，这样的场称为旋涡场或有旋 ... 绕不同方向的方向旋度不相同， (2)有这样一个特殊方向，该方向的方向
www.docin.com/p-734619567.html
轉為繁體網頁
轉為繁體網頁
运筹学解题指导 - 第 80 頁 - Google 圖書結果
https://books.google.com.hk/books?isbn=7302122806 - 轉為繁體網頁
2006
求空格检验数的方法有以下两种: U 闭回路法闭回路是指除起点和终点是同一空格以外, ... 有无穷多最优解,以该空格作闭回路,经闭回路法进行调整可得到另一最优解。原谅我的脑回路吧........ - 百度贴吧
tieba.baidu.com/p/3589957107
轉為繁體網頁
轉為繁體網頁
全电流定律_百度百科
baike.baidu.com/view/2569977.htm
轉為繁體網頁
轉為繁體網頁
运筹学 - 第 88 頁 - Google 圖書結果
https://books.google.com.hk/books?isbn=7302004900 - 轉為繁體網頁
“运筹学”教材编写组 - 1990 - Operations research
... 地产地销廿( 24 )格的请人量 6 是选择闭回路上具有(一 1 )的数字枯中的最小者·即 6 ... 表明例 1 有无穷多最仇解·可在表 3 七 0 中以( · 1 , 1 )为调人格,作闭回路( 1 , 1 )弹性理论基础(第2版)上册: - 第 57 頁 - Google 圖書結果
https://books.google.com.hk/books?isbn=7302045550 - 轉為繁體網頁
2001
并将曲线积分改为闭合的回路积分,就得到 A 点处用应变分量表示的三个( i 吕 l 3 )[DOC]N01
www.iaa.ncku.edu.tw/~jthchan/數據化控制/Note01.doc
高中生没专业学过，出错不负责]
wiki:（我只能看懂这些）
在三维直角坐标系Oxyz中，设向量场
为[2]:8：，分别是x轴、y轴、z轴方向上的单位向量，场的分量P、Q、R具有一阶连续偏导数， 那么在各个坐标上的投影分别为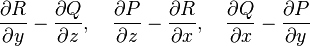：这样的向量。这种表示方法只是便于记忆旋度在直角坐标系中的表达式[3]。感觉已经讲得很清楚了
物理意义：
（斯托克斯定理）当一个向量场的旋度是零时场为保守场，即闭合曲线上F点乘dl积分为零。物理上就是带着物体走一圈场做功为零，如重力场，电场（无磁通量变化）
[0] |
2楼 3楼
2013-11-17 11:37 呜呱星人 只看Ta
老美的书里有一些比较直观的解释。可以去看看他们的新生微积分那类书。
大致是什么意思呢，我也就是个初学者水平，话说的也不是特别清楚。不过我还是可以稍微说说。
想像一个游泳池。进水口在此，排水口在彼。
面积分说的是啥呢？面积分说的是绕着这个进水管画一个封闭曲面，楼主就想象成球面最简单。忽略进水口与排水口连接的水管，认为水在进水口凭空产生，在出水口凭空消失。那么从内向外（由外向内则反）流过这个曲面的水量就可以大致理解为面积分的值。
现在我们来看，假设我们这个曲面画的不囊括进出水口，且水不可压缩，那么流进这个曲面的水必须流出去。流进多少就流出多少，流出多少就流进多少。正负相加，这个面积分得零。（质量守恒定律）
以上是宏观解释，我们再来看微观的（此处微观与分子原子无关，我们假设水是连续的）
场与法向量点积的面积分等于散度的三重积分（高斯-奥斯特罗格拉兹基散度公式）。流体力学的连续性方程告诉我们，密度对时间的导数加上流率的散度等于零。现在水不可压缩，密度不变，那么流率的散度也就是零。求三重积分肯定还是零。也即，面积分等于零。
以上是不囊括进出水口的情况，我们再来讨论复杂一点的，曲面内部有且只有一个进水口的情况（出水口一样，就是正的变成负的）。宏观上看，有水从内向外流出这个曲面。（不要忘记我们假设水在进水口处是凭空产生的）也即面积分大于零
微观上看呢，在进水口处流率（这个词是我胡编乱造的，因为我根本没有系统的学过流体力学）的散度大于零，在别处流率的散度等于零。那么三重积分积下来（如果把进水口想象成点的话就要用到dirac的delta函数，比较麻烦。所以在这里我就只说个大概意思）是大于零的，也即流量的面积分大于零。
再想像曲面囊括两个口，一个排水一个进水。好了，宏观上，我们发现假设假设排水口有点堵的话，进水就比排水多，面积分为正，反之亦然。微观上呢，进水口的散度就比排水口的散度绝对值大，一积分一叠加你就发现三重积分是正的，于是乎向外净流量也是正的。
再想像，这回不是两个三个进出水口了，想像他们是连续分布的。道理差不多，这个曲面里的水盛不下了就要往外跑，曲面里的水太少别出的水就要补进来。这就是高斯-奥氏散度定理。
[0] | 大致是什么意思呢，我也就是个初学者水平，话说的也不是特别清楚。不过我还是可以稍微说说。
想像一个游泳池。进水口在此，排水口在彼。
面积分说的是啥呢？面积分说的是绕着这个进水管画一个封闭曲面，楼主就想象成球面最简单。忽略进水口与排水口连接的水管，认为水在进水口凭空产生，在出水口凭空消失。那么从内向外（由外向内则反）流过这个曲面的水量就可以大致理解为面积分的值。
现在我们来看，假设我们这个曲面画的不囊括进出水口，且水不可压缩，那么流进这个曲面的水必须流出去。流进多少就流出多少，流出多少就流进多少。正负相加，这个面积分得零。（质量守恒定律）
以上是宏观解释，我们再来看微观的（此处微观与分子原子无关，我们假设水是连续的）
场与法向量点积的面积分等于散度的三重积分（高斯-奥斯特罗格拉兹基散度公式）。流体力学的连续性方程告诉我们，密度对时间的导数加上流率的散度等于零。现在水不可压缩，密度不变，那么流率的散度也就是零。求三重积分肯定还是零。也即，面积分等于零。
以上是不囊括进出水口的情况，我们再来讨论复杂一点的，曲面内部有且只有一个进水口的情况（出水口一样，就是正的变成负的）。宏观上看，有水从内向外流出这个曲面。（不要忘记我们假设水在进水口处是凭空产生的）也即面积分大于零
微观上看呢，在进水口处流率（这个词是我胡编乱造的，因为我根本没有系统的学过流体力学）的散度大于零，在别处流率的散度等于零。那么三重积分积下来（如果把进水口想象成点的话就要用到dirac的delta函数，比较麻烦。所以在这里我就只说个大概意思）是大于零的，也即流量的面积分大于零。
再想像曲面囊括两个口，一个排水一个进水。好了，宏观上，我们发现假设假设排水口有点堵的话，进水就比排水多，面积分为正，反之亦然。微观上呢，进水口的散度就比排水口的散度绝对值大，一积分一叠加你就发现三重积分是正的，于是乎向外净流量也是正的。
再想像，这回不是两个三个进出水口了，想像他们是连续分布的。道理差不多，这个曲面里的水盛不下了就要往外跑，曲面里的水太少别出的水就要补进来。这就是高斯-奥氏散度定理。
4楼
2013-11-17 11:50 呜呱星人 只看Ta
现在我们再想像，不是一个曲面，而是两个有一部分共用的封闭曲面。（就假设一个椰子被切一刀，切成的两半套上保鲜膜，再和起来。两片保鲜膜重合在一起）我们现在来计算穿过曲面甲，曲面乙以及曲面甲乙的面积分。在“椰子壳”处一切好说，而再保鲜膜处就有意思了：曲面甲在曲面乙的外部，反之亦然。于是乎保鲜膜甲处的外法向和同一点上保鲜膜乙的外法向相反，而流率是一样的，于是乎在保鲜膜上的面积分甲乙互为相反数。（这很正常，流出甲的水流入乙）于是乎在曲面甲乙上的面积分等于椰子壳上的面积分，不论有没有保鲜膜。
这样我们就可以把一个复杂的图形切割开，切割成简单的，无穷小的，然后把它们叠加起来求出整个积分，证明高斯-奥氏散度公式。
[0] | 这样我们就可以把一个复杂的图形切割开，切割成简单的，无穷小的，然后把它们叠加起来求出整个积分，证明高斯-奥氏散度公式。
5楼
2013-11-17 12:12 呜呱星人 只看Ta
我们再来看stokes公式。思路是差不多的，只不过这里都是伪向量。泡利的讲义有那么一段讲得还可以，就是张量拿过来就用我有点吓一跳。
我们这次来想象一下。。龙卷风。美国人民表示这玩意破坏力还是挺强的。这里的龙卷风呢，可以有各种不同的形状，方圆均可。风的每一点对应着一个力，这个力会对在这一点上运动的物体做功。（至于为什么小物件非要跟着龙卷风的形状走呢。。我不清楚。我们就要求他这样，或者可以给他一个约束力嘛，反正约束力又不做功。而且就算有别的什么力做功也算不到龙卷风头上）
我们还是先从没有龙卷风开始。没有龙卷风不代表没有力，就像没有进水口不代表没有水流一样。就说这个小物块受重力影响吧（牛顿引力场）可能还受电力影响（暂时忽略磁力，磁力比较复杂，但是其实从不做功）可能还受弹簧力影响。
我在重力场中，扔起一块石头，石头落在我手上。重力对石头并没有做功。在电场里仍起一个带电物体，又回来，仍不做功。实际上，这些场的共同点是：在其中运行的物体
[0] | 我们这次来想象一下。。龙卷风。美国人民表示这玩意破坏力还是挺强的。这里的龙卷风呢，可以有各种不同的形状，方圆均可。风的每一点对应着一个力，这个力会对在这一点上运动的物体做功。（至于为什么小物件非要跟着龙卷风的形状走呢。。我不清楚。我们就要求他这样，或者可以给他一个约束力嘛，反正约束力又不做功。而且就算有别的什么力做功也算不到龙卷风头上）
我们还是先从没有龙卷风开始。没有龙卷风不代表没有力，就像没有进水口不代表没有水流一样。就说这个小物块受重力影响吧（牛顿引力场）可能还受电力影响（暂时忽略磁力，磁力比较复杂，但是其实从不做功）可能还受弹簧力影响。
我在重力场中，扔起一块石头，石头落在我手上。重力对石头并没有做功。在电场里仍起一个带电物体，又回来，仍不做功。实际上，这些场的共同点是：在其中运行的物体
7楼 8楼
2013-11-17 12:44 呜呱星人 只看Ta
接上面）这些场的共同特点是：对一个在其中运动轨迹为封闭曲线的物体做得总功为零。这些场叫做保守场。
总功是宏观解释，我们再来看微观解释。stokes公式说的是曲面上场的法向分量面积分（眼熟么？对了和前面那个只差2点，那就是这里的曲面不是闭合的。那里的曲面是个椰子，这里的曲面是张床单。那里是积分场自身，这里是积分他的旋度）等于场在曲面边界上切向分量的线积分。
保守场的旋度为零（关于保守场我们可以说很多，不过都等价）于是乎面积分为零，线积分为零。
我们把龙卷风加回来，绕龙卷风一周，龙卷风做功不为零。微观解释是龙卷风风立场不是保守的，旋度不为零，于是乎积分不为零，总功不为零。
后面的讨论与上面大同小异了，有一点不一样的就是在第二种情况，边界和曲面再给出的时候是没有定向的，而定向的规则是约定俗成而确定的。所以说这一点不用担心床单反过来也能铺的问题。
[0] | 总功是宏观解释，我们再来看微观解释。stokes公式说的是曲面上场的法向分量面积分（眼熟么？对了和前面那个只差2点，那就是这里的曲面不是闭合的。那里的曲面是个椰子，这里的曲面是张床单。那里是积分场自身，这里是积分他的旋度）等于场在曲面边界上切向分量的线积分。
保守场的旋度为零（关于保守场我们可以说很多，不过都等价）于是乎面积分为零，线积分为零。
我们把龙卷风加回来，绕龙卷风一周，龙卷风做功不为零。微观解释是龙卷风风立场不是保守的，旋度不为零，于是乎积分不为零，总功不为零。
后面的讨论与上面大同小异了，有一点不一样的就是在第二种情况，边界和曲面再给出的时候是没有定向的，而定向的规则是约定俗成而确定的。所以说这一点不用担心床单反过来也能铺的问题。
9楼
2014-10-23 16:34 阿达X-Ray 只看Ta
首先建议楼主：要想直观地理解旋度和散度地概念最好不要看国内的书尤其是教材。下面说一下我的理解。不全面，希望能帮到楼主。本人才疏学浅，以下内容尽量不会采用专业术语。
旋度：
首先考虑二维平面：想象一下平面向量场中水平（x轴）和竖直（y轴）分量分别是P（x，y）和Q（x，y）。即A＝P＊i＋Q＊j（i，j分别是水平和竖直方向地单位向量）。那么水平方向上地微增量dX会引起向量场A在竖直方向上地分量Q（x，y）地微增量dQ。这一变化会导致位于点（x，y）处的向量出现由x轴向y轴旋转地趋势，用右手定则判定，会出现一个垂直指向XOY平面外的向量。这个向量就是造成点（x，y）出现顺时针旋转地“漩涡源”（画一下图，可以很明显地看出来。）。同样地，dY会引起dP，但是依照右手定则方向与前者正好相反。那么点（x，y）在这两个“漩涡源”的作用下将如何“旋转”抑或是不旋转呢？很简单，将上述两个旋转向量相加即可。由于选用右手系，所以旋转向量为（（dQ／dX）－（dP／dY））＊k
其中的‘’d“应该是偏导数符号反写的”e“但是我没找到。”k“是z轴方向的单位向量（就是垂直指向纸外的方向）。
下面是3维的情况：向量场此时为A＝P＊i＋Q＊j＋R＊k
如上所述，XOY平面内求得的旋度是一个指向z轴的向量。同理得：指向x轴得旋度向量为（（dR／dY）－（dQ／dz））＊i ；指向y轴得旋度向量为（（dP／dZ）－（dR／dX））＊j 。
所以3为空间中得旋度向量为：（（dR／dY）－（dQ／dz））＊i ＋（（dP／dZ）－（dR／dX））＊j ＋（（dQ／dX）－（dP／dY））＊k 。
哈密顿算子的那个倒三角我敲不出来。
可以用右手形象的体验一下：将手掌伸平，四指指向x轴，y轴垂直与手掌竖直向上（好像手里托着一盘猜一样，OMG，我真佩服自己的想想像力！）设想以下，当dX沿x轴增长时，由于向量A沿y轴方向的增长dQ导致点（x，y）处的向量由x轴向y轴旋转，这时弯曲你的四根手指可以攥成一个拳头，大拇指的指向即旋度向量的方向。
dX同样也会引起水平分量变化dP，dY同样也会引起竖直分量变化dQ。怎么办？这个我就不知道了。不好意思。
散度比较简单，分别对三个变量的方向求偏导数。不说了。
旋度：
首先考虑二维平面：想象一下平面向量场中水平（x轴）和竖直（y轴）分量分别是P（x，y）和Q（x，y）。即A＝P＊i＋Q＊j（i，j分别是水平和竖直方向地单位向量）。那么水平方向上地微增量dX会引起向量场A在竖直方向上地分量Q（x，y）地微增量dQ。这一变化会导致位于点（x，y）处的向量出现由x轴向y轴旋转地趋势，用右手定则判定，会出现一个垂直指向XOY平面外的向量。这个向量就是造成点（x，y）出现顺时针旋转地“漩涡源”（画一下图，可以很明显地看出来。）。同样地，dY会引起dP，但是依照右手定则方向与前者正好相反。那么点（x，y）在这两个“漩涡源”的作用下将如何“旋转”抑或是不旋转呢？很简单，将上述两个旋转向量相加即可。由于选用右手系，所以旋转向量为（（dQ／dX）－（dP／dY））＊k
其中的‘’d“应该是偏导数符号反写的”e“但是我没找到。”k“是z轴方向的单位向量（就是垂直指向纸外的方向）。
下面是3维的情况：向量场此时为A＝P＊i＋Q＊j＋R＊k
如上所述，XOY平面内求得的旋度是一个指向z轴的向量。同理得：指向x轴得旋度向量为（（dR／dY）－（dQ／dz））＊i ；指向y轴得旋度向量为（（dP／dZ）－（dR／dX））＊j 。
所以3为空间中得旋度向量为：（（dR／dY）－（dQ／dz））＊i ＋（（dP／dZ）－（dR／dX））＊j ＋（（dQ／dX）－（dP／dY））＊k 。
哈密顿算子的那个倒三角我敲不出来。
可以用右手形象的体验一下：将手掌伸平，四指指向x轴，y轴垂直与手掌竖直向上（好像手里托着一盘猜一样，OMG，我真佩服自己的想想像力！）设想以下，当dX沿x轴增长时，由于向量A沿y轴方向的增长dQ导致点（x，y）处的向量由x轴向y轴旋转，这时弯曲你的四根手指可以攥成一个拳头，大拇指的指向即旋度向量的方向。
dX同样也会引起水平分量变化dP，dY同样也会引起竖直分量变化dQ。怎么办？这个我就不知道了。不好意思。
散度比较简单，分别对三个变量的方向求偏导数。不说了。
No comments:
Post a Comment