先从运动学开始说起。学习运动学是学习动力学的前提之一。动力学无非两点:受力与运动。
运动学就是处理后者的一个知识要点。它主要分为三块内容:质点运动学、刚体运动学、复合运动分析。
质点运动学是学习面的基础,主要是让你学习一下坐标法、矢量法和自然坐标系下的基本运动判定。高中时代的我们主要是学习这些内容的。
刚体运动学是大学理论力学区别于高中物理的主要部分。把单纯的一个质点看成是三维空间中的刚体,研究的问题就大大复杂了。其主要内容主要是研究如下几点:刚体的平面运动(学会速度的基点法公式)、刚体的定点运动(欧拉角以及Resal坐标系)、刚体的复合运动(复合速度、复合角速度、复合加速度)。
学会了如上的运动学知识可以说你对于物体运动的判定就已经到了一定的高度了(如果将来有机会学习弹性力学,那又会接触到刚体以外的弹性体的运动,物理嘛,就是这样不断拓展的过程。)
对于运动学还有一个重要的知识点,那就是受力分析。静力学就是让你学习受力分析而存在的。他的主要内容在于平面力系的平衡(主矢和主矩平衡的公式)还有摩擦力的一些内容这里不赘述。
现代物理学进步的第一个重要的里程碑就是运用到了能量,所以从能量角度来考虑静力学问题也是非常重要的,所以静力学还有一个重要问题就是虚位移原理(在结构力学中也经常用于平面桁架结构的求解)以及对于变分法的初步认识。这是后面学习最小作用量原理和第二类拉格朗日方程的基础。
最后就是重中之重的动力学了。动力学在高中阶段我们主要学习了质点的牛顿运动定律和三大守恒定律。这些内容需要拓展到刚体,也就是刚提的动量定理,动量矩定理(欧拉动力学方程)还有动能定理。这些要结合之前的运动学一起学习。
然后就是分析力学,也就是第二类拉格朗日方程的运用。这是体现物理学思想进步的一大方法。主要就是写出拉格朗日量然后代入方程求解出运动(需要注意系统的理想、完整、定常性质)
最后就是哈密顿动力学,从数学系学生的角度来看,这是数理结合最为紧密的一块。正如前几位所说的,如果你学习过一些微分几何的话你就会发现:广义坐标就是李群或者流形的参数化,广义速度是个切向量,广义动量是余切向量,泊松括号定义了一个相空间上的测度等等。这些内容还与数学的一个叫做动力系统的分支有关系。
可以说近代物理学有三个E开头的内容是引起物理学革命的,第一个就是理论力学中的Energy,你将会在大一的时候学到。第二个叫做Entropy,熵,你将会在大二学习热力学的时候学习到。第三点叫做Entanglement,纠缠,你将会在大三学习量子力学的时候学习到,经过这些学习,你将会对近代物理学有一个初步的认识。
而理论力学就是第一道难关
理论力学的核心是什么?
学习、学生、物理学专业
按投票排序按时间排序
11 个回答
什么是答案总结? 答案总结
Gongqiu Ting、知乎用户、知乎用户 等人赞同
应该是哈密顿方程及其数学结构。
理论力学里,广义坐标,哈密顿量,泊松括号等概念很不直观。并不像牛顿力学里,位置,速度,能量,动量那样可以由观察实验直接产生这些概念。引入这些抽象物理量的目的在于,它们更能反映经典力学系统中的数学结构,让守恒量的判据尽可能直接的表现在动力学方程中。
为了挖掘力学系统的数学结构,我们要使用很高级的数学语言。学习理论力学没有必要刻意寻找物理量的直觉意义。要先掌握其中的数学基础。强烈建议你学习微分几何与辛几何,然后再看理论力学,用数学语言重新表述一遍,你就会知道那些物理量的必要性了。比如广义坐标就是李群或者流形的参数化,广义速度是个切向量,广义动量是余切向量,泊松括号定义了一个相空间上的泊松代数(同时也是一个李代数)等等。
又看了几位同学的回答,都在谈最小作用量原理。这与我的答案互为补充,角度不同。最小作用量原理是理论力学乃至理论物理的基本假设,各种形式系统都是这一原理应用于在不同对象(质点,刚体,流体,场等)的情况下,按必要地数学语言(前两个是有穷维流形,后两个是无穷维流形)和合理的对称性假设,而构造出来的。
我的答案中强调哈密顿方程的数学结构,说的是在默认最小作用量原理情况下,如何选择最恰当的数学语言描述动力学方程。其实f=ma完全可以体现最小作用量原理,但是不直接,也没有直接呈现守恒量。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
待更新!
最近觉得对哈密顿-雅可比方程(HJE)理解不够深刻。我只看到了哈密顿方程的辛结构而没联系到其中的least-action。
理论力学里,广义坐标,哈密顿量,泊松括号等概念很不直观。并不像牛顿力学里,位置,速度,能量,动量那样可以由观察实验直接产生这些概念。引入这些抽象物理量的目的在于,它们更能反映经典力学系统中的数学结构,让守恒量的判据尽可能直接的表现在动力学方程中。
为了挖掘力学系统的数学结构,我们要使用很高级的数学语言。学习理论力学没有必要刻意寻找物理量的直觉意义。要先掌握其中的数学基础。强烈建议你学习微分几何与辛几何,然后再看理论力学,用数学语言重新表述一遍,你就会知道那些物理量的必要性了。比如广义坐标就是李群或者流形的参数化,广义速度是个切向量,广义动量是余切向量,泊松括号定义了一个相空间上的泊松代数(同时也是一个李代数)等等。
又看了几位同学的回答,都在谈最小作用量原理。这与我的答案互为补充,角度不同。最小作用量原理是理论力学乃至理论物理的基本假设,各种形式系统都是这一原理应用于在不同对象(质点,刚体,流体,场等)的情况下,按必要地数学语言(前两个是有穷维流形,后两个是无穷维流形)和合理的对称性假设,而构造出来的。
我的答案中强调哈密顿方程的数学结构,说的是在默认最小作用量原理情况下,如何选择最恰当的数学语言描述动力学方程。其实f=ma完全可以体现最小作用量原理,但是不直接,也没有直接呈现守恒量。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
待更新!
最近觉得对哈密顿-雅可比方程(HJE)理解不够深刻。我只看到了哈密顿方程的辛结构而没联系到其中的least-action。
实际上就是最小作用量原理。你可以看看朗道的理论力学,基于最小作用原理可以推出拉格朗日方程以及整个理论力学体系。
不过从工科角度而言,等价的原理还有很多,比如虚位移原理等。
要学好理论力学,很重要地就是明确约束是什么,其数学表达是怎么样的。
不过从工科角度而言,等价的原理还有很多,比如虚位移原理等。
要学好理论力学,很重要地就是明确约束是什么,其数学表达是怎么样的。
理论力学的本质是最小作用量原理。对于物理专业的本科生来说最重要的是需要熟练运用第二类拉格朗日方程解决力学问题。
理论力学有三大核心内容:运动学,静力学,动力学。
先上一张我以前总结的知识结构图
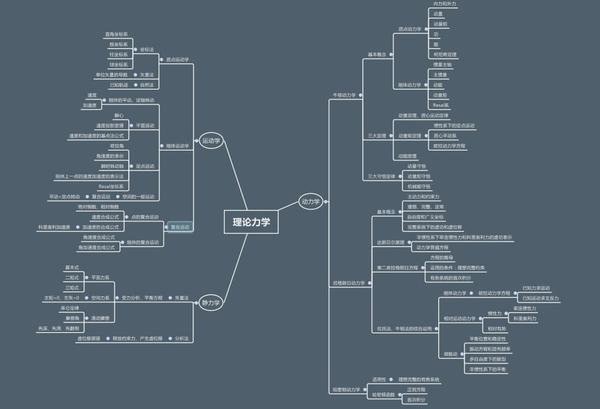
先从运动学开始说起。学习运动学是学习动力学的前提之一。动力学无非两点:受力与运动。
运动学就是处理后者的一个知识要点。它主要分为三块内容:质点运动学、刚体运动学、复合运动分析。
质点运动学是学习面的基础,主要是让你学习一下坐标法、矢量法和自然坐标系下的基本运动判定。高中时代的我们主要是学习这些内容的。
刚体运动学是大学理论力学区别于高中物理的主要部分。把单纯的一个质点看成是三维空间中的刚体,研究的问题就大大复杂了。其主要内容主要是研究如下几点:刚体的平面运动(学会速度的基点法公式)、刚体的定点运动(欧拉角以及Resal坐标系)、刚体的复合运动(复合速度、复合角速度、复合加速度)。
学会了如上的运动学知识可以说你对于物体运动的判定就已经到了一定的高度了(如果将来有机会学习弹性力学,那又会接触到刚体以外的弹性体的运动,物理嘛,就是这样不断拓展的过程。)
对于运动学还有一个重要的知识点,那就是受力分析。静力学就是让你学习受力分析而存在的。他的主要内容在于平面力系的平衡(主矢和主矩平衡的公式)还有摩擦力的一些内容这里不赘述。
现代物理学进步的第一个重要的里程碑就是运用到了能量,所以从能量角度来考虑静力学问题也是非常重要的,所以静力学还有一个重要问题就是虚位移原理(在结构力学中也经常用于平面桁架结构的求解)以及对于变分法的初步认识。这是后面学习最小作用量原理和第二类拉格朗日方程的基础。
最后就是重中之重的动力学了。动力学在高中阶段我们主要学习了质点的牛顿运动定律和三大守恒定律。这些内容需要拓展到刚体,也就是刚提的动量定理,动量矩定理(欧拉动力学方程)还有动能定理。这些要结合之前的运动学一起学习。
然后就是分析力学,也就是第二类拉格朗日方程的运用。这是体现物理学思想进步的一大方法。主要就是写出拉格朗日量然后代入方程求解出运动(需要注意系统的理想、完整、定常性质)
最后就是哈密顿动力学,从数学系学生的角度来看,这是数理结合最为紧密的一块。正如前几位所说的,如果你学习过一些微分几何的话你就会发现:广义坐标就是李群或者流形的参数化,广义速度是个切向量,广义动量是余切向量,泊松括号定义了一个相空间上的测度等等。这些内容还与数学的一个叫做动力系统的分支有关系。
可以说近代物理学有三个E开头的内容是引起物理学革命的,第一个就是理论力学中的Energy,你将会在大一的时候学到。第二个叫做Entropy,熵,你将会在大二学习热力学的时候学习到。第三点叫做Entanglement,纠缠,你将会在大三学习量子力学的时候学习到,经过这些学习,你将会对近代物理学有一个初步的认识。
而理论力学就是第一道难关。
理论力学有三大核心内容:运动学,静力学,动力学。
先上一张我以前总结的知识结构图

先从运动学开始说起。学习运动学是学习动力学的前提之一。动力学无非两点:受力与运动。
运动学就是处理后者的一个知识要点。它主要分为三块内容:质点运动学、刚体运动学、复合运动分析。
质点运动学是学习面的基础,主要是让你学习一下坐标法、矢量法和自然坐标系下的基本运动判定。高中时代的我们主要是学习这些内容的。
刚体运动学是大学理论力学区别于高中物理的主要部分。把单纯的一个质点看成是三维空间中的刚体,研究的问题就大大复杂了。其主要内容主要是研究如下几点:刚体的平面运动(学会速度的基点法公式)、刚体的定点运动(欧拉角以及Resal坐标系)、刚体的复合运动(复合速度、复合角速度、复合加速度)。
学会了如上的运动学知识可以说你对于物体运动的判定就已经到了一定的高度了(如果将来有机会学习弹性力学,那又会接触到刚体以外的弹性体的运动,物理嘛,就是这样不断拓展的过程。)
对于运动学还有一个重要的知识点,那就是受力分析。静力学就是让你学习受力分析而存在的。他的主要内容在于平面力系的平衡(主矢和主矩平衡的公式)还有摩擦力的一些内容这里不赘述。
现代物理学进步的第一个重要的里程碑就是运用到了能量,所以从能量角度来考虑静力学问题也是非常重要的,所以静力学还有一个重要问题就是虚位移原理(在结构力学中也经常用于平面桁架结构的求解)以及对于变分法的初步认识。这是后面学习最小作用量原理和第二类拉格朗日方程的基础。
最后就是重中之重的动力学了。动力学在高中阶段我们主要学习了质点的牛顿运动定律和三大守恒定律。这些内容需要拓展到刚体,也就是刚提的动量定理,动量矩定理(欧拉动力学方程)还有动能定理。这些要结合之前的运动学一起学习。
然后就是分析力学,也就是第二类拉格朗日方程的运用。这是体现物理学思想进步的一大方法。主要就是写出拉格朗日量然后代入方程求解出运动(需要注意系统的理想、完整、定常性质)
最后就是哈密顿动力学,从数学系学生的角度来看,这是数理结合最为紧密的一块。正如前几位所说的,如果你学习过一些微分几何的话你就会发现:广义坐标就是李群或者流形的参数化,广义速度是个切向量,广义动量是余切向量,泊松括号定义了一个相空间上的测度等等。这些内容还与数学的一个叫做动力系统的分支有关系。
可以说近代物理学有三个E开头的内容是引起物理学革命的,第一个就是理论力学中的Energy,你将会在大一的时候学到。第二个叫做Entropy,熵,你将会在大二学习热力学的时候学习到。第三点叫做Entanglement,纠缠,你将会在大三学习量子力学的时候学习到,经过这些学习,你将会对近代物理学有一个初步的认识。
而理论力学就是第一道难关。
我觉得学完理论力学,核心知识:找到多个不同于经典力学且可以相互证明的理论(拉格朗日方程,哈密顿方程)描述物体状态,并让你知道在力学(mechanics)中力(Force)不是一定要存在的,力只是人为规定的许多抽象量之一。不得不说说哈密顿理论,我感觉太抽象了,到后面的广义动量,广义坐标什么的正则化后都已经能够不具有现实物理意义了,但是经过数学的巧妙变换后适用的范围变广多了,但这时候我的物理三观早都毁掉了。。在学习理论力学间我最大的收获是找到一个理论将 几何光学与理论力学 相结合。这个应该是几何光学和力学统一。。。几何光学 的核心是 费马原理,又被称为“最短时间原理”。。与理论力学中第一性原理最小作用量原理 简直毫无违和感。。。这种感觉在高中看到楞次定律和勒夏特列原理一样,心花一下再开放了。专业物理大二,学的不多,如有错误,请及时指正,谢谢。
虚功原理和最小作用量原理吧,两者与牛顿力学都是等价的。
牛顿力学在描述体系时,一般需要用3N个变量来标定(N为质点数)。但是对于有约束情况,这3N个坐标并不是独立变量。所以理论力学非常漂亮的把因为约束而导致的非独立变量剔除掉,仅用s个可以独立变化的坐标来标定体系(s称为自由度,独立变化的坐标称为广义坐标)。
而如何能根据牛顿力学方程F=ma,推导出仅包含广义坐标的方程,需要依靠虚功原理或最小作用量原理。这两个原理都可以在理想约束的条件下(约束力在满足限制条件的的位移上不做功),通过引入虚位移的概念,在不引入约束力的情况下使得方程满足约束条件。进而可以推导出仅包含s个广义坐标和主动力(不用考虑约束力)的拉格朗日方程和哈密顿方程(两者等价,仅是换了一个自变量)。这种描述可以大大的简化牛顿力学在有约束体系的表达方式。
之后的能量积分、循环坐标、泊松括号等概念是建立在拉格朗日方程、哈密顿方程的基础上的。
牛顿力学在描述体系时,一般需要用3N个变量来标定(N为质点数)。但是对于有约束情况,这3N个坐标并不是独立变量。所以理论力学非常漂亮的把因为约束而导致的非独立变量剔除掉,仅用s个可以独立变化的坐标来标定体系(s称为自由度,独立变化的坐标称为广义坐标)。
而如何能根据牛顿力学方程F=ma,推导出仅包含广义坐标的方程,需要依靠虚功原理或最小作用量原理。这两个原理都可以在理想约束的条件下(约束力在满足限制条件的的位移上不做功),通过引入虚位移的概念,在不引入约束力的情况下使得方程满足约束条件。进而可以推导出仅包含s个广义坐标和主动力(不用考虑约束力)的拉格朗日方程和哈密顿方程(两者等价,仅是换了一个自变量)。这种描述可以大大的简化牛顿力学在有约束体系的表达方式。
之后的能量积分、循环坐标、泊松括号等概念是建立在拉格朗日方程、哈密顿方程的基础上的。
我自己的感觉是理论力学就是从各种角度考察系统随时间的演化。
牛顿力学说的是f=ma。
从最小作用量原理的角度,质点的实际运动轨迹要满足作用量取极值,要满足Lagrange方程,这是在位形空间中看。
从相空间看,就要用Hamilton那一套理论,可以把相点的运动当成不可压缩流体,也可以把系统的演化看成连续的以Hamiltonian为生成函数的无穷小正则变换。对于一个有界的系统,还有Poincare Recurrence Theorem这种不可思议的东西。在位形空间里就不是这么有意思。
最后Hamilton-Jacobi方程从某种程度上就是在求一个正则变换,直接把运动理解为对初始条件的一个正则变换。
另外从对称性推导守恒量是比较让人震惊的。关于守恒量我们也可以从几个方面理解,比如在Lagrange那一套理论里用Noether's Theorem,在Hamilton那一套理论里可以用无穷小正则变换和Poisson括号(参见Goldstein),在Hamilton-Jacobi那一套理论里我简单的理解为初始条件是不变的。
===========
以上为大二狗的一派胡言,如有不对还得批判一番。
牛顿力学说的是f=ma。
从最小作用量原理的角度,质点的实际运动轨迹要满足作用量取极值,要满足Lagrange方程,这是在位形空间中看。
从相空间看,就要用Hamilton那一套理论,可以把相点的运动当成不可压缩流体,也可以把系统的演化看成连续的以Hamiltonian为生成函数的无穷小正则变换。对于一个有界的系统,还有Poincare Recurrence Theorem这种不可思议的东西。在位形空间里就不是这么有意思。
最后Hamilton-Jacobi方程从某种程度上就是在求一个正则变换,直接把运动理解为对初始条件的一个正则变换。
另外从对称性推导守恒量是比较让人震惊的。关于守恒量我们也可以从几个方面理解,比如在Lagrange那一套理论里用Noether's Theorem,在Hamilton那一套理论里可以用无穷小正则变换和Poisson括号(参见Goldstein),在Hamilton-Jacobi那一套理论里我简单的理解为初始条件是不变的。
===========
以上为大二狗的一派胡言,如有不对还得批判一番。
135 人关注该问题
换一换
相关问题
- 牛顿摆的理论解释是什么? 5 个回答
- 如何学好热力学? 3 个回答
- 如何学好理论物理? 13 个回答
- 长尾理论有什么弊端? 7 个回答
- 《流体力学》难么,学之前要看些什么,《理论力学》? 39 个回答
- 长尾理论是一个骗局吗? 17 个回答
- 热力学中的压强到底是什么意思? 12 个回答
- 流体力学发展到现在为什么还要进行风洞试验?风洞试验能解决哪些理论计算解决不了的问题? 32 个回答
- 用热力学基本定律来解释物理现象是否等于没有解释? 16 个回答
- 相同材料,同样重量,同样长度,仅截面形状不同,它们的力学特性是否相同,为什么? 4 个回答
這是 Google 對 http://www.douban.com/group/topic/18649065/ 的快取。 這是該網頁於 2015年7月31日 19:09:35 GMT 顯示時的快照。
怎么由运动方程导出拉格朗日量?
来自: k1a2(但曾相见便相知,相见何如不见时) 2011-03-28 22:29:49
我看的是沈惠川的经典力学,带电粒子的拉格朗日量似乎是毫无目的地刚好碰巧凑出来的.电磁场更过分,直接就从不变量猜出来了。。有没有一些普遍一点的方法?
好吧,给个具体问题:
F_i =q ε_ijk β_j ∂_k φ
其中β = v/c
好吧,给个具体问题:
F_i =q ε_ijk β_j ∂_k φ
其中β = v/c
-
我是个怀疑论者.Lagrange方程的其中一个条件,在动力学中x与dx/dt独立.什么叫"独立"?既然可以在Lagrange中可以无限制地添加x,dx/dt,d2x/dt2..,那是否就可以往里面添加同样"动力学学独立"的(d/dt)^(1/2)x之类的东西?Lagrange方程真的可以包含一切吗?
k1a2 (但曾相见便相知,相见何如不见时) 2011-03-30 22:50:35
虽然是个初学者,但我也知道在历史上曾经有过各类微分方程解的存在性,唯一性(这点Lagrange量不满足),和稳定性的讨论.于是我想也应该有微分方程所对应的变分形式存在性类似的讨论吧?还有"形式一致性"(这个词是我自创的...实在不知道怎么表达),即保证整数阶的微分方程所对应的变分形式中不会出现分数阶的项.
-
嗯,我当时看Landau力学的时候就觉得速度和位移独立是不可理喻的。如果给定位移关于时间的函数,速度、加速度以及更高阶时间导数不是都确定了吗,为什么说它们是独立的呢?好吧,我们先听从Landau先生的教诲,那么马上要问的问题是,那加速度什么的是不是也可以放到Lagrangian里面去呢?我想这也是楼主的困惑。
Everett (╮(╯▽╰)╭ ~(= ̄ U  ̄=)~) 2011-03-31 14:14:37
正当我困惑着呢,Landau先生接下去写到:位移和速度已经完备动力学系统的自由度,加速度和更高级导数并不独立于位移和速度,因此Lagrangian只需作为位移和速度的函数,而不需要进一步包含加速度等自变量了。看到这里我顿时就崩溃了,同时开始崇拜Landau先生居然可以在写书的时候就知道读者要问的问题。接下来有一段话来分析支持这个论点,大意是知道位移和速度就可以预测下一个时刻的位移,如此就可以得到轨迹,加速度属于冗余信息。
后来我才知道,正是因为我们基于Lagrangian出发考虑,才会出现独立性疑难。因为如果位移和速度不独立,我们就不能理解什么叫Lagrangian对速度求偏导(而保持位移不变)。但是,如果我们直接从作用量入手,并且将作用量理解成位移的泛函,就可以避免这个问题。所谓泛函就是函数的函数。位移关于时间的变化是一个函数 x(t),作用量泛函的作用就是把这个函数映射到一个实数上去。这时候,位移就是作用量泛函唯一的自变量,速度、加速度等等都由位移函数决定,不是独立的。求运动方程的时候只要对作用量变分,并令结果等于0就可以了。在变分的过程中,加速度什么的都会自动跑出来,就没有什么偏导不偏导的烦恼了。
-
2011-03-31 14:14:37 Everett
眼鏡大俠 (不要再消磨时光了!) 2011-03-31 22:55:33
11楼
嗯,我当时看Landau力学的时候就觉得速度和位移独立是不可理喻的。如果给定位移关于时间的函数,速度、加速度以及更高阶时间导数不是都确定了吗,为什么说它们是独立的呢?好吧,我们先听从Landau先生的教诲,那么马上要问的问题是,那加速度什么的是不是也可以放到Lagrangian里面去呢?我想这也是楼主的困惑。
正当我困惑着呢,Landau先生接下去写到:位移和速度已经完备动力学系统的自由度,加速度和更高级导数并不独立于位移和速度,因此Lagrangian只需作为位移和速度的函数,而不需要进一步包含加速度等自变量了。看到这里我顿时就崩溃了,同时开始崇拜Landau先生居然可以在写书的时候就知道读者要问的问题。接下来有一段话来分析支持这个论点,大意是知道位移和速度就可以预测下一个时刻的位移,如此就可以得到轨迹,加速度属于冗余信息。
后来我才知道,正是因为我们基于Lagrangian出发考虑,才会出现独立性疑难。因为如果位移和速度不独立,我们就不能理解什么叫Lagrangian对速度求偏导(而保持位移不变)。但是,如果我们直接从作用量入手,并且将作用量理解成位移的泛函,就可以避免这个问题。所谓泛函就是函数的函数。位移关于时间的变化是一个函数 x(t),作用量泛函的作用就是把这个函数映射到一个实数上去。这时候,位移就是作用量泛函唯一的自变量,速度、加速度等等都由位移函数决定,不是独立的。求运动方程的时候只要对作用量变分,并令结果等于0就可以了。在变分的过程中,加速度什么的都会自动跑出来,就没有什么偏导不偏导的烦恼了。
---------------------------------------
E大的11樓讓我頓時有了看朗道顯示著作的興趣
-
物理体系,给出速度就已经确定状态了,轨迹也确定了(这个时候确定的是轨迹族),如果给出初始速度就唯一确定轨迹了,这是常微分方程的存在与唯一性定理保证的。
Tabris (人生的意义就是“等待与希望”) 2011-04-02 13:45:31
但相对性原理不需要给出一个初始位置,只需要相对位置就可以了(这是对于多粒子体系,单粒子体系连初始位置都不需要给定)
不过说到体系的状态,这个含义可能会很广, 比如带电或不带电的状态肯定不同,但在没有电磁场的情况下,他们的相轨迹可以相同,所以这里的状态包含了可观察的状态,或者说是你想要观察的状态,那么对于纯粹的运动,位移是唯一关注的量,所以确定位移速度与位移初始就成为一个完全集,如果你还要考虑能量,那么质量也必然应该引入,或者是把速度换成是动量。
到了量子状态,这个概念就会更加明确(力学量完全)
不知道是否解决了 cmp0xff 同学的疑惑
-
2011-04-02 11:00:15 点阵 回楼上,从没听说过这样的信仰,照你这样说,Lagrange方程不能导出Newton方程咯。
留空 2011-04-03 20:45:06
物理学的基本信仰是对称性和守恒律,一种对称性对应一种守恒量。不守恒的量严格来说应该驱逐出物理学。由对称性给出lagrangian,由lagrangian给出运动方程。
再问楼上,为什么要找lagrangian?
量子化呗。
牛顿力学中描述运动状态既需要位置,也需要速度。因此牛顿第二定律左边可以出现状态量(r,v),右边可以出现状态的时间变化率(v,a)。实际上物理学没有一个单一信仰,你所说的以对称性确定Lagrangian的方法在场论中常用,但是就像Weinberg I里的解释:对一个string theoretist来说,人们先需要观察到弦的一种振动模式,再由此导出满足规范对称性的effective field theory。
- 先不论量子化是不是找lagrangian的根本出发点,显然量子化是一条理由,但不充分。Hamiltonian也能量子化,而且守恒,况且量子化方法也不只这一种。
点阵 (Je veux seulement l'oublier) 2011-04-05 11:07:04
你定义的状态量本身就有问题,速度是状态量,加速度就是状态变化率了?一阶导数是状态量,高阶就不是了。“由于从拉氏量导出运动方程时会对t求一次导,因此我们一般假定拉氏量中只有速度而没有加速度。 ”
这么说导出的运动方程只能含有不超过2阶的导数。但在阻尼力的问题中,方程含高阶导数。所以我说照你的意思,lagrange方程导不出经典力学。
newton方程分左右,我也是第一次听说,求出处。
-
只看了两天拉格朗日方程的很惶恐的说道:
孤立奇点 2011-04-05 14:17:00
那个~~~我似乎觉得在牛顿动力学方程里是不会出现三阶或以上的高阶微分方程吧。那时候,世界没那么复杂,给一个“力”的概念就搞定全部。力就是位置对时间的二阶导数。
然后,拉格朗日函数给定后,世界就定了。假如体系里一个约束都没有,运动状态也是定下来的,至少拉格朗日等人时这样看的。我个人觉得这很符合直觉,就是,如果我啥都不知道,那我知道啥?“啥都不知道”也是一种状态。
当我们确定物理景观里的某种变化,(我们确实认为在变,但不是任意变),这时构成我们关心的物理运动。这个“不任意”,就是我们明确知道,他受到了某种约束。当体系受到一定约束后,他就只能做某一类运动了。
拉格朗日关注的是在那一类运动中,在所谓“主动力”情况下,构成的运动,他认为这就是我们见到的运动。若跟你见到的不一样的话,只能说明我们的约束没找齐,或主动力没找齐。所有经验和实验“都”表明,只要我们找的齐。拉格朗日方程就给的出来。若要从理论角度来证明,只要认为牛顿定律是正确的就行,可以证明拉格朗日动力学方程与牛顿动力学方程在数学上最后将给出相同的微分方程的解。(虚功原理等价于矢量受力平衡)+(达朗贝尔等效原理)使得拉格朗日的研究对象都是“平衡”的!而且和牛顿动力学方程构建的物理基础是一致的。拉格朗日还发现如果我们不是先知道“力”的情况,而是先知道体系“能”的情况,我们同样能得到体系运动情况。牛顿从来就不觉得“能”是必要的,“力”才是基础。但现在“能”也可以是基础了!
关于为什么在拉格朗日函数里,广义速度是独立于广义坐标,那是因为那是拉格朗日函数,他是表征着体系的能量情况,体系的能量当然和体系的所谓动能,和所谓势能有关,而且,我们的世界在无约束情况下是可以有任意的动能和势能的,总不能说这样的势能就一定是那样的势能。虽然这是事实,但是在得到拉格朗日方程之后。所谓速度与位矢相对独立,是一个存在于逻辑里的情况,而不是某个物理事实。
至于说到“加速度”这个东西,是没有的,因为一个显而易见的事实是,加速度是一种和力在数学上等价的东西。而现在“力”是没有的了。达朗贝尔原理,使得体系总是“平衡”。这种平衡,在牛顿看来是力的结果。但是拉格朗日认为,是拉格朗日函数,即体系能量的结果。
若你告诉牛顿,这个体系“力”的情况,原则上他就懂得在逻辑上认识了这个运动以前或以后是怎样的,而且事实跟其思想一致。你你告诉拉格朗日体系能量的话,他也可以得到同样的运动结论。
而最基本的是,他们都能看到的唯一东西是“运动”也是他们共同看到的事实。而事实是不为个人背后的思想而转移的。
牛顿为啥不搞个加加速度呢?因为他不觉得世界上有一个这样的客观事实(独立于位置的)来支配这个情况。而人类有能力“找到”他所谓的“力”,然后就好了。人类同样能“找到”拉格朗日函数。构造“力”就不可避免要用到加速度的概念,但是构造体系动能和势能却不需要。
大概就这样,我的初步理解~~~多谢指正。
-
说个这样的事情吧,或许对大家有帮助。
善龍 (吾心安处惟故宅) 2011-04-05 16:11:45
你们看标准的场论书上都极少出现外力这个概念,但这个量在你们的讨论中有很重要的意义,因为牛顿力学说了,外力是速度改变的原因,甚至还定量的给出了外力是如何改变速度的(牛二)。
但牛顿力学没有解释外力是如何来的,这样就有两种不同的看法,一种是外力是外部因素,于是我们可以建立起一整套拉格朗日力学,‘前人之述备矣’;当然还有不服气的人,他们把研究的系统扩充到将外力也包含进来,作为研究的对象,这样问题就难缠了,他们试图去解释力本身是如何随时间空间改变的,以及力的改变是如何随时间改变的....当然这就是你们说的三次及高次导。
似乎这是一个子子孙孙无穷尽矣的难题,让我们回到较为简单的问题:什么是力?在牛顿那个时代,有一个力是理解得比较清楚的,引力,至少比弹簧振子的弹力用胡克定律来描述这种东西要深刻得多,万有引力理论是一个很强大的理论,你看,它把这些子子孙孙无穷尽矣的难题全解决了(我是说它的各阶导数都可以明显的写出来),如果我们的世界只有万有引力就好了,但事实上没有这么简单:很显然,这个理论甚至无法解释弹力和摩擦力这些司空见惯的力。
这时候,我们不得不提库伦,安培,韦伯,法拉第这一帮人,他们研究了除了引力之外日常生活中可以接触到的力:电力和磁力。最后,集大成者,麦克斯韦将这两种力统一起来。这些理论,都能把那些高阶导数什么的一次性解决,不留下尾巴,比如说库伦定律就讲清楚了两个带电球之间的力作为时间空间的函数是平法反比定律。
在自牛顿开始的经典物理学(我主要是指微积分这个可以定量分析物理的工具出现之后)发展了200多年之后,我们生活中可以看到的力,引力和电磁力都很漂亮的被解决了,上帝好像也并不比我们强多少么,你看本来难缠的无穷阶导一次性就解决了。但故事还没有结束,实际上才刚刚开始,按照标准的书上的说法,飘来三朵乌云,革命了。
-
正则量子化都是从拉氏量出发,这是因为就算你能找到体系的能量表达式,没有Lagrangian你也找不到正则动量,于是就无法对其赋予正则对易关系。此外,如果不知道Lagrangian我们也无法知道体系有什么约束。
留空 2011-04-06 19:07:51
对经典力学来说,速度显然是状态量之一,表出系统能量、动量都需要速度,你总不能说这些都不是状态量吧。但加速度就不是状态量,也没有任何其它状态量需要加速度才能表出。
“但在阻尼力的问题中,方程含高阶导数。所以我说照你的意思,lagrange方程导不出经典力学。”
这我真没听说过,你说的是辐射阻尼?辐射阻尼不能严格看做一个力,这个我们都知道。更一般的说,假设某种力与质点速度的导数(即位矢高阶导数)有关,那么这种非保守力就可以质点自动加速,这将导致能量不守恒——这也是把辐射阻尼看做真实力时的困难之一。
-
用对称性当然是可以的,但仅限于非相对论量子力学。在场论里似乎并没有把共轭场算符看做场平移操作生成元的,因为我们实际上也基本不处理场算符的本征态。而在通常情况下,因为位置算符和动量算符的共轭性我们都知道,而单粒子Hamiltonian又常可以用p,q表出,确实可以直接从系统能量表达式过渡到Hamiltonian。但一般情况下这是不可能的,比如场的正则量子化中,能量表达式是用场量(如E,B)表达的,如果没有Lagrangian量我们就不知道如何用场量表出共轭场算符,因此就无法做正则量子化。更有甚者,如果我们要处理的体系具有singular Lagrangian(比如电磁场),那么从Lagrangian到Hamiltonian的过渡还能给出系统约束,而系统的约束条件直接影响了系统的规范不变性和对Poisson括号的修正,因此就算我猜出了共轭场算符的形式也无法直接进行正则量子化。
留空 2011-04-06 20:47:24
以上这些内容在Dirac的Lectures on Quantum Mechanics(这是一本专论约束体系正则量子化的书),和Weinberg I中都有详细论述。两本书都很明确地指出:正则量子化的出发点是Lagrangian
你的回应
回应请先 登录 , 或 注册推荐到广播
34409 人聚集在这个小组
加入小组 最新话题 ( 更多 )
- 申请读博,导师回复等问题求问 (数理小肥羊)
- 为什么光速c是一个最大值? (宇宙小顽童)
- 觉得初中物理可以和高中物理结结合看 求建议 (代三个表)
- 电磁波可以是纵波吗? (孤立奇点)
- 关于时空理论的一些新想法(总结) (质子)
勾选后,我们将限制其他用户的复制操作,并给予提醒
查看演示
禁止转载演示
这是你的回答正文
当其他人想复制你的一段回答
复制将受限,同时会弹出提醒
如需转载,请通过私信或评论联系我
选择语言










No comments:
Post a Comment