自发对称性破缺与Higgs机制
Author:
最早Higgs机制是在凝聚态物理中出现,早期并不想高能物理那样,凝聚态理论中的Higgs机制仍不是相对论形式。
我们不妨先从凝聚态物理的量子多体理论的角度来讨论Higgs机制。一个复标量场(Higgs场)具有两个自由度:振幅场 以及相位场
以及相位场 ,即分离变量形式为
,即分离变量形式为

我们可以首先对Higgs机制采用二次量子化的量子多体理论的语言来进行描述。对复标量场进行平移,我们可以来研究一下这种真空自发破缺的动力学行为(自发性的原因是因为并非哈密顿量造成真空的对称性破缺,也即非动力学因素,而是真空基态的简并使得它被破坏)。由于 场在哈密顿量中具有
场在哈密顿量中具有 自作用能,引起真空凝聚的时零点能是非零的,并使得真空发生相变(能谱由原来的抛物面变为“墨西哥帽”形状)而处于
自作用能,引起真空凝聚的时零点能是非零的,并使得真空发生相变(能谱由原来的抛物面变为“墨西哥帽”形状)而处于 场的Bose相干凝聚态。
场的Bose相干凝聚态。
你在这里面混淆了UV发散和IR发散的事情
辐射修正那是QED里面对树图的高阶修正过程(即计入真空极化影响),涉及内线动量圈积分(UV发散),因而要进行重整化。这所谓发散抵消实际上是一套流程手续,首先进行正规化(Pauli-Villars正规化或者维数正规化)分离出发散部分,对裸的Lagrangian引入抵消Lagrangian后边得到重整化Lagrangian,把发散部分吸收进重整化常数里头(也就是遮起来当作没看见;或者说归入一定能标下的本底部分,有限能标下根本无法激发仪器也探测不到)。于是裸量等于重整化常数乘以重整化量,我们测量的物理量实际上都是重整化量。见:http://www.blogbus.c
而IR发散则相对于UV发散来说良性得多,确实按照场论,IR发散是由于内线低能粒子所导致。在QED中其重要程度不如UV发散,毕竟在QED里面低能实光子和虚光子引起的IR发散是正好抵消的(在传播子分母处添加无穷小质量,然后圈图和树图抵消);QED里面这个对观察量没什么影响,长波极限的低能软光子根本没有任何仪器会探测到。对于相变物理则更为有意思,临界点附近,系统对称性破缺的那部分相互作用场激发的恢复模会软化(低至零动量就变成Goldstone模),长波涨落就导致长程序破坏使得关联长度发散。所以说长波涨落的存在是因为有零质量的Goldstone模。一般IR发散都和零质量粒子联系在一起。因为它能量没有能隙,在任何物理过程中都可能产生无穷无尽的零质量粒子,这些粒子能量低到实验探测不到。技术处理上的表现就如计算元激发传播子的时,软模的出现会使得涨落波矢为零时发散。序参量(如磁化强度)则是一定对称性破缺的软模凝聚形成。在大于3维的空间里IR发散就没有了(当然假设UV发散已经截断了),因为高维中涨落影响程度降低了,因此Wilson发展了$4-\epsilon$维数展开法(维数正规化)。传统的Landau理论其实是考虑最低标度(原子间)的涨落波矢积掉之后的平均场结果,认为短程涨落才起到作用,这一来没考虑更大标度(集团间)的涨落对长程序的影响;RG手续则相当于是对所有标度(关联长度发散)的涨落波矢都逐层积掉。
一些例子,譬如铁磁体的磁振子在居里点温度软化,以及气液相变点声子软化促使凝聚,表面张力近乎为零呈现两相不可分辨,Peirls相变在$2k_F$点声子软化....这些软模出现都导致响应发散,也就是一种IR发散。所以说实际上IR发散只不过是人为地使用了物理图像不正确的理论导致。见:http://www.douban.co
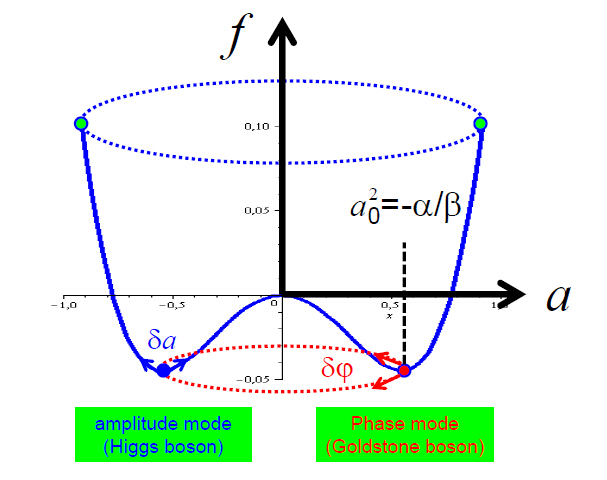
计算场激发的平方谱可发现正比于 场质量项平方,由于是复的场,因此还出现一支零质量Goldstone谱(在计入规范场耦合后会消失)。现在考虑单模复标量场与
场质量项平方,由于是复的场,因此还出现一支零质量Goldstone谱(在计入规范场耦合后会消失)。现在考虑单模复标量场与 电磁场耦合,利用超流体理论中的处理方法“Bogouliubov变换”,变到新的“准粒子”真空态来讨论。在新的真空本底上,中性
电磁场耦合,利用超流体理论中的处理方法“Bogouliubov变换”,变到新的“准粒子”真空态来讨论。在新的真空本底上,中性 场的元激发(经过变换后哈密顿量对角化,它对应于Green函数的极点)具有实质量。而原来横向极化的两个零质量光子变成了带有效质量的重光子,同时这个重光子还具有一个纵向极化自由度。从而原来无质量三个场:
场的元激发(经过变换后哈密顿量对角化,它对应于Green函数的极点)具有实质量。而原来横向极化的两个零质量光子变成了带有效质量的重光子,同时这个重光子还具有一个纵向极化自由度。从而原来无质量三个场: 场以及两个极化方向的电磁场分量,在经过真空相变合并为同一种重光子的三个极化自由度。从相互作用看,这个过程既依赖于
场以及两个极化方向的电磁场分量,在经过真空相变合并为同一种重光子的三个极化自由度。从相互作用看,这个过程既依赖于 场的自相互作用引起的真空相变,也依赖于
场的自相互作用引起的真空相变,也依赖于 场与
场与 场以及电磁场之间的相互作用耦合。从规范理论的角度来看,
场以及电磁场之间的相互作用耦合。从规范理论的角度来看, 场真空凝聚是导致
场真空凝聚是导致 规范不变性的破坏,因此产生恢复对称性的零能Goldstone模。在加入
规范不变性的破坏,因此产生恢复对称性的零能Goldstone模。在加入 规范场耦合后,通过规范变换后讲拉格朗日量重新规范化后,Goldstone谱消失,取而代之的有效理论中规范Boson变成具有有效质量的激发。这就是所谓规范Boson吃掉Goldstone粒子后产生了质量。开头说过Higgs机制其实来源于凝聚态物理。最早是Anderson在描述超导体时引入,其中电子对形成的Cooper对就相当于
规范场耦合后,通过规范变换后讲拉格朗日量重新规范化后,Goldstone谱消失,取而代之的有效理论中规范Boson变成具有有效质量的激发。这就是所谓规范Boson吃掉Goldstone粒子后产生了质量。开头说过Higgs机制其实来源于凝聚态物理。最早是Anderson在描述超导体时引入,其中电子对形成的Cooper对就相当于 复标量场的地位,其中相位场就是超导相干相位。其真空凝聚破坏
复标量场的地位,其中相位场就是超导相干相位。其真空凝聚破坏 对称性,形成电子系统BEC凝聚,这样一来,Goldstone模产生,意味着超导基态随相位变化是零能隙的,作用动量算后符产生相位梯度形成整体动量,因此产生超流性质的超导电流;它与电磁场耦合使得产生有效质量,由于光子带了有效质量了之后,拉格朗日量中就会多出
对称性,形成电子系统BEC凝聚,这样一来,Goldstone模产生,意味着超导基态随相位变化是零能隙的,作用动量算后符产生相位梯度形成整体动量,因此产生超流性质的超导电流;它与电磁场耦合使得产生有效质量,由于光子带了有效质量了之后,拉格朗日量中就会多出 的项,导出的Maxwell方程形式就会发生变化,Coulomb作用在导体中是Yukawa型的,磁场也指数衰减,从中就可得出穿透深度。于此同时,Goldstone模消失,超导电流在穿透区域也消失。这些也就是唯象理论London方程给出的内容,此即Minssner效应。此外,此理论还告诉人们穿透深度与超导能隙有关。
的项,导出的Maxwell方程形式就会发生变化,Coulomb作用在导体中是Yukawa型的,磁场也指数衰减,从中就可得出穿透深度。于此同时,Goldstone模消失,超导电流在穿透区域也消失。这些也就是唯象理论London方程给出的内容,此即Minssner效应。此外,此理论还告诉人们穿透深度与超导能隙有关。
在弱电统一模型中,真空手征对称性破缺也会产生真空相变,场的Yukawa型耦合赋予新真空下粒子质量。这也是通常高能物理里面所指的Higgs机制( 规范场的Higgs机制),电弱统一的GSW机制中规范对称性破缺方式是
规范场的Higgs机制),电弱统一的GSW机制中规范对称性破缺方式是 破缺为
破缺为 ,(手征对称性破缺)会产生三个Goldstone模,费米子场
,(手征对称性破缺)会产生三个Goldstone模,费米子场 通过Higgs机制中Yukawa型耦合
通过Higgs机制中Yukawa型耦合 (在标准模型中,可以证明这种耦合类型是费米子与标量场唯一可重整化耦合方式),由于Higgs场
(在标准模型中,可以证明这种耦合类型是费米子与标量场唯一可重整化耦合方式),由于Higgs场 具有非零真空期望值,因此这一耦合对真空态展开后就得到fermion质量项
具有非零真空期望值,因此这一耦合对真空态展开后就得到fermion质量项 ,这样一来使得其中三种粒子获得质量,即
,这样一来使得其中三种粒子获得质量,即 ;剩下一个维持零质量的即光子。 在标准模型中, 所有基本粒子的质量都来源于电弱统一理论中的规范对称性自发破缺。
;剩下一个维持零质量的即光子。 在标准模型中, 所有基本粒子的质量都来源于电弱统一理论中的规范对称性自发破缺。
这里面,系统的对称性自发破缺实际上是个很微妙的事情。一个物理系统的真空态是由 拉格朗日量所确定的,或者准确地说是由于其中含有的有效势 决定; 然而系统却不具有拉格朗日量所具有的对称性,这是为什么呢?其中的原因在于许多物理系统都具有简并的真空态,如果把所有这些简并的真空态视为一个集合,它的确与 拉格朗日量具有同样的对称性。 但物理上真实情况是真空态只是该集合中的一个态,这个态往往不具有整个集合所具有的对称性,这就造成了对称性的自发破缺。如果一个量子系统的基态是简并的,那么系统的物理基态难道不应该是这些简并态的某种量子叠加吗? 这种量子叠加态如在量子力学中所见到那样,往往会破除原有的基态简并性(我们通常做简并微扰就是这样),并且使真正的基态具有与原先简并基态的集合相同的对称性。在这种情况下,对称性自发破缺岂不是不存在了?对于有限体系来说确实如此(除非有什么机制,比如对称性禁止简并基态间的相互耦合)。但在量子场论中通常假定体系的空间体积趋于无穷(凝聚态物理里面的量子多体系统也满足这一点),这时不同真空态之间的相互耦合趋于零,严格的对称性自发破缺只发生在这种情形下。
决定; 然而系统却不具有拉格朗日量所具有的对称性,这是为什么呢?其中的原因在于许多物理系统都具有简并的真空态,如果把所有这些简并的真空态视为一个集合,它的确与 拉格朗日量具有同样的对称性。 但物理上真实情况是真空态只是该集合中的一个态,这个态往往不具有整个集合所具有的对称性,这就造成了对称性的自发破缺。如果一个量子系统的基态是简并的,那么系统的物理基态难道不应该是这些简并态的某种量子叠加吗? 这种量子叠加态如在量子力学中所见到那样,往往会破除原有的基态简并性(我们通常做简并微扰就是这样),并且使真正的基态具有与原先简并基态的集合相同的对称性。在这种情况下,对称性自发破缺岂不是不存在了?对于有限体系来说确实如此(除非有什么机制,比如对称性禁止简并基态间的相互耦合)。但在量子场论中通常假定体系的空间体积趋于无穷(凝聚态物理里面的量子多体系统也满足这一点),这时不同真空态之间的相互耦合趋于零,严格的对称性自发破缺只发生在这种情形下。
*Nambu-Goldstone定理
规范对称性破缺产生保护无能隙Goldstone激发,然后通过相应规范场耦合的加入,那么应该是都可以的。这就是所谓Nambu-Goldstone定理的内容,其适用于描述任意连续对称性破缺恢复模式。连续对称性的群代数结构是Lie群,破坏掉的对称性即是少掉了一些Lie代数生成元,减少的生成元个数对应着Goldstone粒子数目。规范场就是破坏了的生成元所构成的Lie导数,对应的场分量就可以“吃掉”那多出来的Goldstone粒子。
最早Higgs机制是在凝聚态物理中出现,早期并不想高能物理那样,凝聚态理论中的Higgs机制仍不是相对论形式。
我们不妨先从凝聚态物理的量子多体理论的角度来讨论Higgs机制。一个复标量场(Higgs场)具有两个自由度:振幅场
我们可以首先对Higgs机制采用二次量子化的量子多体理论的语言来进行描述。对复标量场进行平移,我们可以来研究一下这种真空自发破缺的动力学行为(自发性的原因是因为并非哈密顿量造成真空的对称性破缺,也即非动力学因素,而是真空基态的简并使得它被破坏)。由于
你在这里面混淆了UV发散和IR发散的事情
辐射修正那是QED里面对树图的高阶修正过程(即计入真空极化影响),涉及内线动量圈积分(UV发散),因而要进行重整化。这所谓发散抵消实际上是一套流程手续,首先进行正规化(Pauli-Villars正规化或者维数正规化)分离出发散部分,对裸的Lagrangian引入抵消Lagrangian后边得到重整化Lagrangian,把发散部分吸收进重整化常数里头(也就是遮起来当作没看见;或者说归入一定能标下的本底部分,有限能标下根本无法激发仪器也探测不到)。于是裸量等于重整化常数乘以重整化量,我们测量的物理量实际上都是重整化量。见:http://www.blogbus.c
而IR发散则相对于UV发散来说良性得多,确实按照场论,IR发散是由于内线低能粒子所导致。在QED中其重要程度不如UV发散,毕竟在QED里面低能实光子和虚光子引起的IR发散是正好抵消的(在传播子分母处添加无穷小质量,然后圈图和树图抵消);QED里面这个对观察量没什么影响,长波极限的低能软光子根本没有任何仪器会探测到。对于相变物理则更为有意思,临界点附近,系统对称性破缺的那部分相互作用场激发的恢复模会软化(低至零动量就变成Goldstone模),长波涨落就导致长程序破坏使得关联长度发散。所以说长波涨落的存在是因为有零质量的Goldstone模。一般IR发散都和零质量粒子联系在一起。因为它能量没有能隙,在任何物理过程中都可能产生无穷无尽的零质量粒子,这些粒子能量低到实验探测不到。技术处理上的表现就如计算元激发传播子的时,软模的出现会使得涨落波矢为零时发散。序参量(如磁化强度)则是一定对称性破缺的软模凝聚形成。在大于3维的空间里IR发散就没有了(当然假设UV发散已经截断了),因为高维中涨落影响程度降低了,因此Wilson发展了$4-\epsilon$维数展开法(维数正规化)。传统的Landau理论其实是考虑最低标度(原子间)的涨落波矢积掉之后的平均场结果,认为短程涨落才起到作用,这一来没考虑更大标度(集团间)的涨落对长程序的影响;RG手续则相当于是对所有标度(关联长度发散)的涨落波矢都逐层积掉。
一些例子,譬如铁磁体的磁振子在居里点温度软化,以及气液相变点声子软化促使凝聚,表面张力近乎为零呈现两相不可分辨,Peirls相变在$2k_F$点声子软化....这些软模出现都导致响应发散,也就是一种IR发散。所以说实际上IR发散只不过是人为地使用了物理图像不正确的理论导致。见:http://www.douban.co

计算场激发的平方谱可发现正比于
在弱电统一模型中,真空手征对称性破缺也会产生真空相变,场的Yukawa型耦合赋予新真空下粒子质量。这也是通常高能物理里面所指的Higgs机制(
这里面,系统的对称性自发破缺实际上是个很微妙的事情。一个物理系统的真空态是由 拉格朗日量所确定的,或者准确地说是由于其中含有的有效势
*Nambu-Goldstone定理
规范对称性破缺产生保护无能隙Goldstone激发,然后通过相应规范场耦合的加入,那么应该是都可以的。这就是所谓Nambu-Goldstone定理的内容,其适用于描述任意连续对称性破缺恢复模式。连续对称性的群代数结构是Lie群,破坏掉的对称性即是少掉了一些Lie代数生成元,减少的生成元个数对应着Goldstone粒子数目。规范场就是破坏了的生成元所构成的Lie导数,对应的场分量就可以“吃掉”那多出来的Goldstone粒子。
No comments:
Post a Comment