什么是分数量子霍尔效应？
按投票排序按时间排序
5 个回答
这个问题略犀利... 分数量子霍尔效应(Fractional Quantum Hall Effect ~ FQH)是霍尔效应家族里最复杂也是最 fancy 的之一... 下面是豆瓣物理组 E 大为霍尔效应家族做的一副图, FQH 就是最右下角的那个.
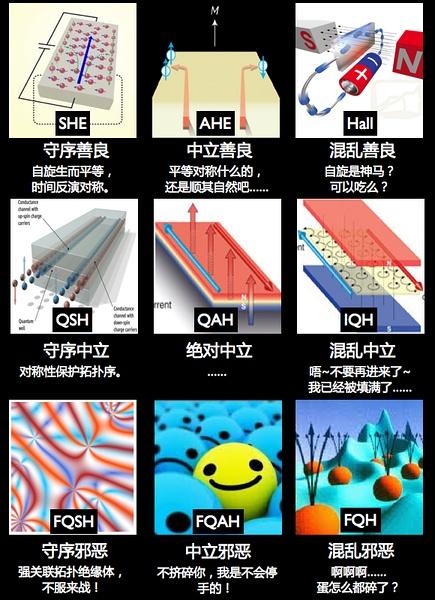
问这个问题的人想必没有太多凝聚态物理的背景, 我还是尽可能从头讲起.
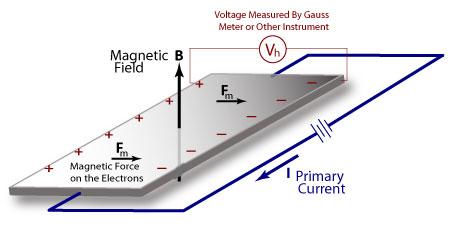造成这个现象的原因大家是熟知的: 电子在磁场中受到 Lorentz 力而偏转, 在导体两端积累, 在导体中建立起电场从而在产生电势差. 这个电压被称为霍尔电压. 霍尔效应一个显著的特征是霍尔电压与磁场强度成正比. 下面是 Hall 当年发现该效应时的原始数据:
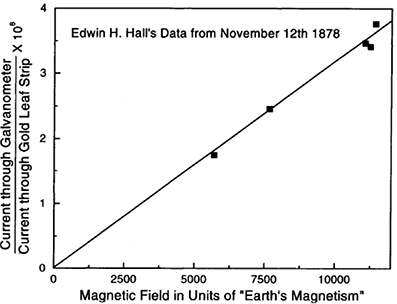
在整整一百多年后的1980年, 德国物理学家 von Klitzing 发现了所谓的量子霍尔效应. 之所以要等这么久才能实现这一效应, 主要是由于理想的二维电子气难以实现. 在半导体技术高度发展之后, 人们才能在"金属-氧化物-半导体场效应晶体管"(MOSFET)中实现比较理想的二维电子气. 除此之外, 观察到这一效应还需要极低温(1.5K)和强磁场(18T). von Klitzing 因此获得了1985年诺贝尔物理学奖.
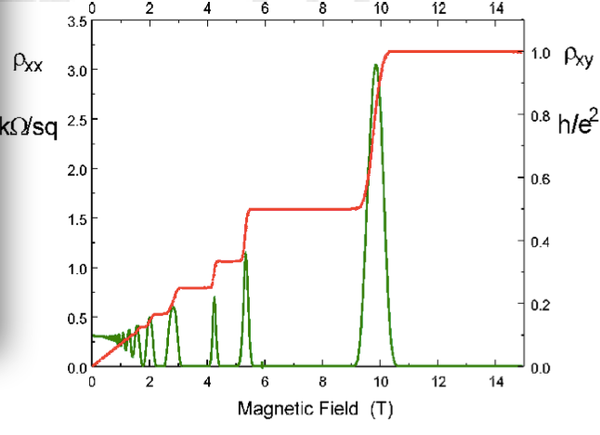
量子霍尔效应与霍尔效应最大的不同之处在于横向电压对磁场的响应明显不同. 横向电阻是量子化的, 由此我们称这一现象为量子霍尔效应:
尽管从整体趋势上看, 横向电阻(图中红线. 电阻的定义为电压/电流, 实验时电流恒定, 因此横向电阻就相当于横向电压)随着磁场强度增大而线性增大, 但在这一过程中却形成了若干横向电阻不变的平台. 这些平台所对应的电阻是"量子电阻"
除以一个整数 n, 对应图中平台的"1, 0.5, 0.33, 0.25, 0.2"等位置. 量子霍尔效应也称作整数量子霍尔效应(Integer Quantum Hall Effect ~ IQH). 原始霍尔效应所对应的区域是磁场强度 B 很小区域. 从图中可以看见磁场强度很小时横向电阻与磁场强度确实成线性关系.
除此之外, 量子霍尔效应中的纵向电阻(图中绿线)的随磁场的变化也很奇特: 在横向电阻达到平台时, 纵向电阻竟然为零! 在原始霍尔效应时, 纵向电阻随磁场几乎是不变化的, 这对应图中磁场强度很小时纵向电阻确实近似是一个常数.
量子霍尔效应其背后对应的物理机制, 通俗地说, 可以用下图来解释:
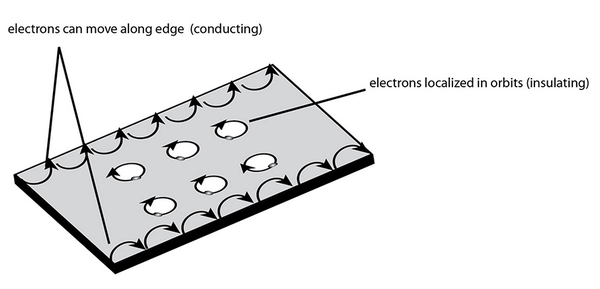在强磁场下, 导体内部的电子受 Lorentz 力作用不断沿着等能面转圈(Lorentz 力不做功!). 如果导体中存在杂质, 尤其是带电荷的杂质, 将会影响等能面的形状. 实际上, 导体内部的电子只能在导体内部闭合的等能面上做周期运动, 而不能参与导电. (因此在很纯净的样品中反而观察不到量子霍尔效应!)
在量子霍尔效应中, 真正参与导电的实际上是电子气边缘的电子. 而边缘的电子转圈转到一半就会打到边界, 受到反弹, 再次做半圆运动, 由此不断前进. 这种在边界运动的电子, 与通常在导体内部运动的电子不同, 它不是通过不断碰撞, 类似扩散的方式前进的. 而是几乎不与其他电子碰撞, 直接到达目的地, 像一颗子弹. 因此这种现象在物理学中被称为弹道输运(ballistic transport). 显然在这种输运机制中产生的电阻不与具体材料有关, 只与电子本身所具有的性质有关. 因此横向电阻总是
, 其中 n 是一个正整数. 之所以与 n 有关, 粗略地说, 是因为磁场小到一定的程度, 就会同时使更多的电子进行弹道输运. 进行的电子越多, 横向电阻越小.
量子霍尔效应中的这种参与导电的"边界态"是当今凝聚态物理重要的兴趣所在之一. "边界"和"表面"有其重要的拓扑性质, 所谓"拓扑绝缘体"也与它们紧密相关. 事实上, von Klitzing 是在德国的 Würzburg 大学发现的量子霍尔效应. 28年后, 同样是在 Würzburg 大学, 同样是 von Klitzing 之前所在的研究组, Molenkamp 等人第一次在实验上发现了拓扑绝缘体: 碲化汞. 由此也可以发现一项重要的工作的完成不是一蹴而就的, 其背后必然有着深厚的积累.
的 n 不仅可以取正整数, 还出现了 n=1/3 这样一个分数的平台! 这就是分数量子霍尔效应. 之后他们制造出了更纯的样品, 更低的温度, 更强的磁场. 85mK 和 280kG, 这是人类第一次在实验室中实现如此低的温度和如此强的磁场(地磁场是 mG 的量级). 这样的实验技术令人叹为观止.
他们也因此观察到了更加丰富的结构(下图不是原始结果而是实验技术进一步提高之后的结果. 参考: The Fractional Quantum Hall Effect. ):
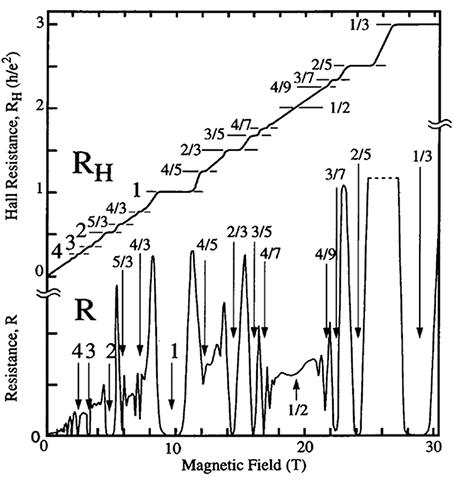根据之前对 n 的解释, n 不可能是分数, 因为不可能有分数个电子同时进行弹道输运. 之前的解释不适用! 最早美国物理学家 Laughlin 给出了一个比较令人信服的解释, 他因此和崔琦与 Stormer 分享了1998年诺贝尔物理学奖.
导体中电子中的相互作用主要有: 电子-杂质, 电子-电子. 之前在解释整数量子霍尔效应时, 我们忽略了电子与电子的相互作用. 而在现在这种样品极为纯净的情况下, 我们不能忽略这一相互作用. 因为电子之间的相互作用很强, 导致电子之间的关联也很强. "牵一发而动全身", 这时我们再用"一个电子"的图像去看问题就不合适了. 为了解决这一问题, 其中一种看法是"混合粒子". 就像质子是由三个夸克组成的一样, 我们可以人为地将处于磁场中的(电子)看作没有磁场时的(电子+量子磁通量). 我们将(电子+量子磁通)人为地看成一个整体, 即"混合粒子". 在这种看法下, 我们会发现"混合粒子"之间近似没有相互作用. 这样我们就将一个强相互作用的问题转化成了一个无相互作用的问题. 对于 n=1/3 的情形, 就是一个电子与三个量子磁通相结合成了一个"混合粒子". 这样所谓分数量子霍尔效应就是"混合粒子"的整数量子霍尔效应. 由于一个电子现在附着了三个量子磁通, 这就解释了分数量子霍尔效应中的 n=1/3. 示意图如下, 穿过电子的三根线即为三个量子磁通:
这一解释虽然看起来合理, 但至今也有很多争议. 分数化是强关联系统一个典型特征. 而强关联系统是当今凝聚态物理学重要的一个分支. 高温超导等许多重要的现象都被认为与此相关. 在这个领域还有大量问题等待人类去回答和探索.
有关量子霍尔效应有一篇十分入门的综述: http://arxiv.org/abs/0909.1998. 推荐给感兴趣的物理系同学.
问这个问题的人想必没有太多凝聚态物理的背景, 我还是尽可能从头讲起.
- 霍尔效应
造成这个现象的原因大家是熟知的: 电子在磁场中受到 Lorentz 力而偏转, 在导体两端积累, 在导体中建立起电场从而在产生电势差. 这个电压被称为霍尔电压. 霍尔效应一个显著的特征是霍尔电压与磁场强度成正比. 下面是 Hall 当年发现该效应时的原始数据: - 量子霍尔效应
在整整一百多年后的1980年, 德国物理学家 von Klitzing 发现了所谓的量子霍尔效应. 之所以要等这么久才能实现这一效应, 主要是由于理想的二维电子气难以实现. 在半导体技术高度发展之后, 人们才能在"金属-氧化物-半导体场效应晶体管"(MOSFET)中实现比较理想的二维电子气. 除此之外, 观察到这一效应还需要极低温(1.5K)和强磁场(18T). von Klitzing 因此获得了1985年诺贝尔物理学奖.
量子霍尔效应与霍尔效应最大的不同之处在于横向电压对磁场的响应明显不同. 横向电阻是量子化的, 由此我们称这一现象为量子霍尔效应:
尽管从整体趋势上看, 横向电阻(图中红线. 电阻的定义为电压/电流, 实验时电流恒定, 因此横向电阻就相当于横向电压)随着磁场强度增大而线性增大, 但在这一过程中却形成了若干横向电阻不变的平台. 这些平台所对应的电阻是"量子电阻"除此之外, 量子霍尔效应中的纵向电阻(图中绿线)的随磁场的变化也很奇特: 在横向电阻达到平台时, 纵向电阻竟然为零! 在原始霍尔效应时, 纵向电阻随磁场几乎是不变化的, 这对应图中磁场强度很小时纵向电阻确实近似是一个常数.
量子霍尔效应其背后对应的物理机制, 通俗地说, 可以用下图来解释:
在强磁场下, 导体内部的电子受 Lorentz 力作用不断沿着等能面转圈(Lorentz 力不做功!). 如果导体中存在杂质, 尤其是带电荷的杂质, 将会影响等能面的形状. 实际上, 导体内部的电子只能在导体内部闭合的等能面上做周期运动, 而不能参与导电. (因此在很纯净的样品中反而观察不到量子霍尔效应!)在量子霍尔效应中, 真正参与导电的实际上是电子气边缘的电子. 而边缘的电子转圈转到一半就会打到边界, 受到反弹, 再次做半圆运动, 由此不断前进. 这种在边界运动的电子, 与通常在导体内部运动的电子不同, 它不是通过不断碰撞, 类似扩散的方式前进的. 而是几乎不与其他电子碰撞, 直接到达目的地, 像一颗子弹. 因此这种现象在物理学中被称为弹道输运(ballistic transport). 显然在这种输运机制中产生的电阻不与具体材料有关, 只与电子本身所具有的性质有关. 因此横向电阻总是
量子霍尔效应中的这种参与导电的"边界态"是当今凝聚态物理重要的兴趣所在之一. "边界"和"表面"有其重要的拓扑性质, 所谓"拓扑绝缘体"也与它们紧密相关. 事实上, von Klitzing 是在德国的 Würzburg 大学发现的量子霍尔效应. 28年后, 同样是在 Würzburg 大学, 同样是 von Klitzing 之前所在的研究组, Molenkamp 等人第一次在实验上发现了拓扑绝缘体: 碲化汞. 由此也可以发现一项重要的工作的完成不是一蹴而就的, 其背后必然有着深厚的积累.
- 分数量子霍尔效应
他们也因此观察到了更加丰富的结构(下图不是原始结果而是实验技术进一步提高之后的结果. 参考: The Fractional Quantum Hall Effect. ): 根据之前对 n 的解释, n 不可能是分数, 因为不可能有分数个电子同时进行弹道输运. 之前的解释不适用! 最早美国物理学家 Laughlin 给出了一个比较令人信服的解释, 他因此和崔琦与 Stormer 分享了1998年诺贝尔物理学奖. 导体中电子中的相互作用主要有: 电子-杂质, 电子-电子. 之前在解释整数量子霍尔效应时, 我们忽略了电子与电子的相互作用. 而在现在这种样品极为纯净的情况下, 我们不能忽略这一相互作用. 因为电子之间的相互作用很强, 导致电子之间的关联也很强. "牵一发而动全身", 这时我们再用"一个电子"的图像去看问题就不合适了. 为了解决这一问题, 其中一种看法是"混合粒子". 就像质子是由三个夸克组成的一样, 我们可以人为地将处于磁场中的(电子)看作没有磁场时的(电子+量子磁通量). 我们将(电子+量子磁通)人为地看成一个整体, 即"混合粒子". 在这种看法下, 我们会发现"混合粒子"之间近似没有相互作用. 这样我们就将一个强相互作用的问题转化成了一个无相互作用的问题. 对于 n=1/3 的情形, 就是一个电子与三个量子磁通相结合成了一个"混合粒子". 这样所谓分数量子霍尔效应就是"混合粒子"的整数量子霍尔效应. 由于一个电子现在附着了三个量子磁通, 这就解释了分数量子霍尔效应中的 n=1/3. 示意图如下, 穿过电子的三根线即为三个量子磁通:
这一解释虽然看起来合理, 但至今也有很多争议. 分数化是强关联系统一个典型特征. 而强关联系统是当今凝聚态物理学重要的一个分支. 高温超导等许多重要的现象都被认为与此相关. 在这个领域还有大量问题等待人类去回答和探索.
有关量子霍尔效应有一篇十分入门的综述: http://arxiv.org/abs/0909.1998. 推荐给感兴趣的物理系同学.
知乎用户
收起
匿名用户、Zeng Junkai、易小丫 赞同
根据Laughlin的解释，说白了就是在散射极少的纯凈二维电子气中电子间相互作用变得重要了。形成的复合费米子构成了能量更低的基态。而低能量的基态的复合费米子比如带电荷3e，对应的霍尔平台就是三分之一。
真是想怎么解释就怎么解释。要不是搞了个极端条件也不可能看不到。于是乎为了闷声大发财，江湖各个门派都勤加修炼。最好能炼化出个奇葩毒物，再配合接近0k的寒冰真气，祭出38T紫霞神功。然后对着乱糟糟的数据折腾出看不见的平台和噪音一样的峰和谷，然后在science上搞出个大新闻。
然后其他门派谁也搞不出来，天朝于是一狠心也有了超低温和强磁场中心。强烈建议上太空再去搞一番，说不定能搞出个无理数霍尔效应
真是想怎么解释就怎么解释。要不是搞了个极端条件也不可能看不到。于是乎为了闷声大发财，江湖各个门派都勤加修炼。最好能炼化出个奇葩毒物，再配合接近0k的寒冰真气，祭出38T紫霞神功。然后对着乱糟糟的数据折腾出看不见的平台和噪音一样的峰和谷，然后在science上搞出个大新闻。
然后其他门派谁也搞不出来，天朝于是一狠心也有了超低温和强磁场中心。强烈建议上太空再去搞一番，说不定能搞出个无理数霍尔效应
第一次答题，只是个拙劣的搬运工
首先经典霍尔效应由德国物理学家Hall在1879年发现
然后 量子Hall效应-----1980年,德国物理学家冯.克利岑(Von Klitzing)发现
再然后 分数量子Hall效应-----1982年,普林斯顿大学的美籍华裔教授崔 琦和Stoemer 发现
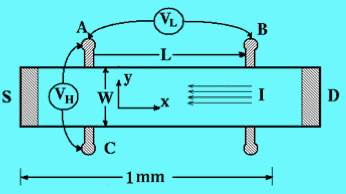
大家都知道量子效应产生的原理是导电板放置在垂直于它的磁场中，载流子在磁场中运动收洛伦兹力而偏转形成的导致了在垂直于原有电流和磁场方向上的电势差。设这个电势差为U，原有电流为I,定义霍尔电阻RH=U/I=I*B/(n*Q*d），其中d为导电板厚度，Q为载流子所带电荷量，n为载流子浓度。
那么基本定义就给出来了，下面先说经典量子霍尔效应，也就是整数型量子霍尔效应(nteger Quantum Hall Effect)
在1980年克里岑（Von Klitzing）在1.5K温度和18.9T磁场下测量金属-氧化物-半导体效应晶体管的霍尔电阻时发现，其霍尔电阻总是h/e^2的整数倍（h为普朗克常数，e为电子电量），这种现象称为量子霍尔效应。
1982年崔琦等人发现分数量子霍尔效应（Fractional Quantum Hall Effect），即RH可以是h/e^2的1/3、2/3、2/5……倍。
下面是一些实验数据
Integer Quantum Hall Effect in a GaAs-GaAlAs heterojunction, recorded at 30mK.
The diagonal component xx of resistivity, which shows regions of zero resistance corresponding to each QHE plateau xy.
xy=h/ne2
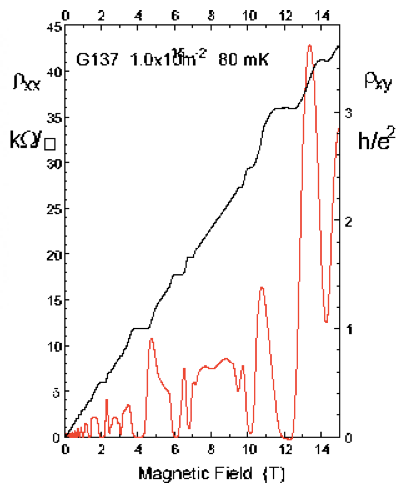
Fractional Quantum Hall Effect
In high mobility semiconductor heterojunctions the integer quantum Hall effect (IQHE) plateaux are much narrower than for lower mobility samples. Between these narrow IQHE more plateaux are seen at fractional filling factors, especially 1/3 and 2/3. This is the fractional quantum Hall effect (FQHE) whose discovery in 1982 was completely unexpected.
The figure shows the fractional quantum Hall effect in a GaAs-GaAlAs heterojunction, recorded at 30mK. Also included is the diagonal component of resistivity, which shows regions of zero resistance corresponding to each FQHE plateau.
Carriers density: 1.0X1015cm-2
The principle series of fractions that have been seen are listed below. They generally get weaker going from left to right and down the page:
参考资料
《电磁学》徐游
另外量子霍尔反常效应也很火，lz可以自行维基百科看看什么的
首先经典霍尔效应由德国物理学家Hall在1879年发现
然后 量子Hall效应-----1980年,德国物理学家冯.克利岑(Von Klitzing)发现
再然后 分数量子Hall效应-----1982年,普林斯顿大学的美籍华裔教授崔 琦和Stoemer 发现
大家都知道量子效应产生的原理是导电板放置在垂直于它的磁场中，载流子在磁场中运动收洛伦兹力而偏转形成的导致了在垂直于原有电流和磁场方向上的电势差。设这个电势差为U，原有电流为I,定义霍尔电阻RH=U/I=I*B/(n*Q*d），其中d为导电板厚度，Q为载流子所带电荷量，n为载流子浓度。
那么基本定义就给出来了，下面先说经典量子霍尔效应，也就是整数型量子霍尔效应(nteger Quantum Hall Effect)
在1980年克里岑（Von Klitzing）在1.5K温度和18.9T磁场下测量金属-氧化物-半导体效应晶体管的霍尔电阻时发现，其霍尔电阻总是h/e^2的整数倍（h为普朗克常数，e为电子电量），这种现象称为量子霍尔效应。
1982年崔琦等人发现分数量子霍尔效应（Fractional Quantum Hall Effect），即RH可以是h/e^2的1/3、2/3、2/5……倍。
下面是一些实验数据
Integer Quantum Hall Effect in a GaAs-GaAlAs heterojunction, recorded at 30mK.
The diagonal component xx of resistivity, which shows regions of zero resistance corresponding to each QHE plateau xy.
xy=h/ne2
Fractional Quantum Hall Effect
In high mobility semiconductor heterojunctions the integer quantum Hall effect (IQHE) plateaux are much narrower than for lower mobility samples. Between these narrow IQHE more plateaux are seen at fractional filling factors, especially 1/3 and 2/3. This is the fractional quantum Hall effect (FQHE) whose discovery in 1982 was completely unexpected.
The figure shows the fractional quantum Hall effect in a GaAs-GaAlAs heterojunction, recorded at 30mK. Also included is the diagonal component of resistivity, which shows regions of zero resistance corresponding to each FQHE plateau.
Carriers density: 1.0X1015cm-2
The principle series of fractions that have been seen are listed below. They generally get weaker going from left to right and down the page:
- 1/3, 2/5, 3/7, 4/9, 5/11, 6/13, 7/15...
- 2/3, 3/5, 4/7, 5/9, 6/11, 7/13...
- 5/3, 8/5, 11/7, 14/9...
- 4/3, 7/5, 10/7, 13/9...
- 1/5, 2/9, 3/13...
- 2/7, 3/11...
- 1/7....
参考资料
《电磁学》徐游
另外量子霍尔反常效应也很火，lz可以自行维基百科看看什么的
No comments:
Post a Comment