麦克斯韦-玻尔兹曼分布[编辑]
维基百科,自由的百科全书
这个分布可以视为一个三维向量的大小,它的分量是独立和正态分布的,其期望值为0,标准差为
 。如果
。如果 的分布为
的分布为 ,那么
,那么 。
。目录
[隐藏]麦克斯韦-玻尔兹曼分布的物理应用[编辑]
麦克斯韦-玻尔兹曼分布形成了分子运动论的基础,它解释了许多基本的气体性质,包括压强和扩散。麦克斯韦-玻尔兹曼分布通常指气体中分子的速率的分布,但它还可以指分子的速度、动量,以及动量的大小的分布,每一个都有不同的概率分布函数,而它们都是联系在一起的。麦克斯韦-玻尔兹曼分布可以用统计力学来推导(参见麦克斯韦-玻尔兹曼统计)。它对应于由大量不相互作用的粒子所组成、以碰撞为主的系统中最有可能的速率分布,其中量子效应可以忽略。由于气体中分子的相互作用一般都是相当小的,因此麦克斯韦-玻尔兹曼分布提供了气体状态的非常好的近似。
在许多情况下(例如非弹性碰撞),这些条件不适用。例如,在电离层和空间等离子体的物理学中,特别对电子而言,重组和碰撞激发(也就是辐射过程)是重要的。如果在这个情况下应用麦克斯韦-玻尔兹曼分布,就会得到错误的结果。另外一个不适用麦克斯韦-玻尔兹曼分布的情况,就是当气体的量子熱波長与粒子之间的距离相比不够小时,由于有显著的量子效应也不能使用麦克斯韦-玻尔兹曼分布。另外,由于它是基于非相对论的假设,因此麦克斯韦-玻尔兹曼分布不能做出分子的速度大于光速的概率为零的预言。
推导[编辑]
麦克斯韦最初的推导假设了三个方向上的表现都相同,但后来在玻尔兹曼的一个推导中利用分子运动论去掉了这个假设。现在,麦克斯韦-玻尔兹曼分布可以轻易地从能量的玻尔兹曼分布推出:动量向量的分布[编辑]
下列所述的推导,与詹姆斯·克拉克·麦克斯韦描述的推导和后来由路德维希·玻尔兹曼描述的具有较少假设的推导都有很大不同。它与玻尔兹曼在1877年的探讨比较接近。对于“理想气体”(由基态的非相互作用原子所组成)的情况,所有能量都是动能的形式。宏观粒子的动能与动量的关系为:
可以证明:
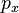 、
、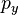 和
和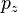 的乘积,其方差为
的乘积,其方差为 。此外,可以看出动量的大小呈麦克斯韦-玻尔兹曼分布,其中
。此外,可以看出动量的大小呈麦克斯韦-玻尔兹曼分布,其中 。
。能量的分布[编辑]
利用p² = 2mE,以及动量的大小的分布函数(参见以下速率分布的章节),我们便得出能量的分布:速度向量的分布[编辑]
认识到速度的概率密度函数fv与动量的概率密度函数成正比: 、
、 和
和 的乘积,但方差为
的乘积,但方差为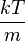 。还可以看出,对于速度向量[vx, vy, vz],麦克斯韦-玻尔兹曼速度分布是三个方向上的分布的乘积:
。还可以看出,对于速度向量[vx, vy, vz],麦克斯韦-玻尔兹曼速度分布是三个方向上的分布的乘积: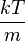 。正如所预料的,对于静止的气体,在任何方向上的平均速度都是零
。正如所预料的,对于静止的气体,在任何方向上的平均速度都是零


![\frac{N_i}{N} =
\frac{1}{Z}
\exp \left[
-\frac{p_x^2 + p_y^2 + p_z^2}{2mkT}
\right]
\qquad\qquad (3)](https://upload.wikimedia.org/math/8/f/5/8f527127e252ab832d3cae3e3ef3c2d3.png)
![f_\mathbf{p} (p_x, p_y, p_z) =
\frac{c}{Z}
\exp \left[
-\frac{p_x^2 + p_y^2 + p_z^2}{2mkT}
\right].
\qquad\qquad (4)](https://upload.wikimedia.org/math/a/b/b/abb62eba6fbe952980c6fa4d5f57618c.png)

![f_\mathbf{p} (p_x, p_y, p_z) =
\left( \frac{1}{2 \pi mkT} \right)^{3/2}
\exp \left[
-\frac{p_x^2 + p_y^2 + p_z^2}{2mkT}
\right].
\qquad\qquad (6)](https://upload.wikimedia.org/math/c/7/1/c719a3700cd88ff5886b1d1d002a0ba6.png)
![f_E\,dE=f_p\left(\frac{dp}{dE}\right)\,dE =2\sqrt{\frac{E}{\pi(kT)^3}}~\exp\left[\frac{-E}{kT}\right]\,dE. \qquad \qquad(7)](https://upload.wikimedia.org/math/0/b/d/0bd1fa1f40fdbca865f37627c98a7518.png)



![f_\mathbf{v} (v_x, v_y, v_z) =
\left(\frac{m}{2 \pi kT} \right)^{3/2}
\exp \left[-
\frac{m(v_x^2 + v_y^2 + v_z^2)}{2kT}
\right],
\qquad\qquad](https://upload.wikimedia.org/math/0/6/3/0632be7dcc1140795c8d8aa071ee70db.png)

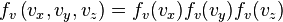
![f_v (v_i) =
\sqrt{\frac{m}{2 \pi kT}}
\exp \left[
\frac{-mv_i^2}{2kT}
\right].
\qquad\qquad](https://upload.wikimedia.org/math/2/9/5/295ead2949493bff9984603c3e07cd27.png)
No comments:
Post a Comment