http://www.docin.org/p-1078843457.html
若ω为1次微分形式,则dω为2次微分形式。一般地,1次微分形式可写为ω=f(x)dx,2次微分形式可写为
通常一个并矢具有九个分量。因此,有时也写成三个分量的形式,而每一分量为一矢量
[PPT]第四章:格林函数ppt
web.xidian.edu.cn/bailu/files/20130201_195401.ppt
轉為繁體網頁
2013年2月1日 - 这种求解数学物理方程的方法即经典的格林函数法,又称为点源函数法或 ... 2)通常结果用一个含有格林函数的有限积分表示,物理意义清晰,便于以 ...轉為繁體網頁
三个矢量格林函数的辐射条件结合在一起,构成了并矢格林函数的辐射条件
天氣是大氣分子的運動,政治是人的活動。氣候變化是物理現象,是無數大氣分子隨機運動的結果,可以預測;政治难以预测 因为人心叵測
微分形式与同调论浅析
通常一个并矢具有九个分量。因此,有时也写成三个分量的形式,而每一分量为一矢量
三个矢量格林函数的辐射条件结合在一起,构成了并矢格林函数的辐射条件
[PPT]第四章:格林函数ppt
并矢既不是点积,也不是叉积,而是矢量的直积或直乘。因为其结果已经超出了原来的矢量空间,所以属于外积的一种
通常一个并矢具有九个分量。因此,有时也写成三个分量的形式,而每一分量为一矢量
三个矢量格林函数的辐射条件结合在一起,构成了并矢格林函数的辐射条件
[PPT]第四章:格林函数ppt
web.xidian.edu.cn/bailu/files/20130201_195401.ppt
轉為繁體網頁
2013年2月1日 - 这种求解数学物理方程的方法即经典的格林函数法,又称为点源函数法或 ... 2)通常结果用一个含有格林函数的有限积分表示,物理意义清晰,便于以 ...轉為繁體網頁
并矢既不是点积,也不是叉积,而是矢量的直积或直乘。因为其结果已经超出了原来的矢量空间,所以属于外积的一种
前面已经介绍了一阶张量的概念,实际上二阶张量是最常用的张量。二阶以上(含二阶)的张量统称为高阶张量。在介绍高阶张量之前,我们先介绍一下矢量的直积。
矢量的直积是矢量之间最简单的一种乘法运算,其结果是张量,所以也叫做矢量的张量积,俗称并矢。举例说明如下:
设三维白线性空间中的任意两个矢量的线性表出分别为
与
则两个矢量的直积就是一个并矢,属于二阶张量的一种,可记为
注意:并矢的先后次序一般不可交换。即
并矢既不是点积,也不是叉积,而是矢量的直积或直乘。因为其结果已经超出了原来的矢量空间,所以属于外积的一种。所谓直积运算就是一个矢量的所有线性组合项遍乘另一个矢量的所有线性组合项,类似于多项式乘法。如上例即
可见三维空间中的一个二阶张量共有9个分量。本例的基矢都是自然基矢(协变基矢),分量都是逆变分量,所以这个张量属于一个二阶逆变张量。
如果用爱因斯坦求和约定,上述并矢(二阶张量)还可以简洁地表示为
注意:两对哑标相乘时必须区别开。
其中基矢的并矢 叫做基张量,本例中的基张量是两个基矢的并矢,所以属于二阶基张量。基张量对应的线性组合系数
叫做基张量,本例中的基张量是两个基矢的并矢,所以属于二阶基张量。基张量对应的线性组合系数 叫做张量的分量。对于两个n维矢量的并矢,有时也用完整的一组
叫做张量的分量。对于两个n维矢量的并矢,有时也用完整的一组 个分量表示其运算结果(一个二阶张量),即
个分量表示其运算结果(一个二阶张量),即
 叫做基张量,本例中的基张量是两个基矢的并矢,所以属于二阶基张量。基张量对应的线性组合系数
叫做基张量,本例中的基张量是两个基矢的并矢,所以属于二阶基张量。基张量对应的线性组合系数 叫做张量的分量。对于两个n维矢量的并矢,有时也用完整的一组
叫做张量的分量。对于两个n维矢量的并矢,有时也用完整的一组 个分量表示其运算结果(一个二阶张量),即
个分量表示其运算结果(一个二阶张量),即
矢量的直积运算还可以采用分量矩阵形式表示。如上例可表示为
一组9个基张量也可以用矩阵表示为
矢量的直积运算可以推广到多个矢量的并矢,即高阶张量。如三个矢量的直积(三重并矢)abc是一个三阶张量
四个矢量的并矢abcd是一个四阶张量
依此类推。为简便起见,张量可以只用一个大写字母(比如T)表示,代表阶数的横线通常可以省略。
当然最常用的是二阶张量,那么二阶张量的定义是什么?且听下回分解。
(作者:周法哲2009-10-21于广东)
(原创)什么是一阶张量?(图)
进入张量的概念
上一回说到,张量概念的前提是坐标变换,而坐标变换的核心关键是基矢变换矩阵(过渡矩阵)A。在同一空间里,当坐标变换时,所有的参量按照其变换规律可以分成两大类:随A协调一致地变换者叫做协变量;“逆转而变”者叫做逆变量。那么一阶张量究竟是什么样的量呢?本文先介绍一阶逆变张量的定义。
一般地,在n维空间的任一坐标系中给定一组有序的数
如果当坐标基矢按某个过渡矩阵A变换时,而这一组数X却按A的转置逆矩阵B变换,即变为
则称这一组数为一个一阶逆变张量。通常用上标变量表示。
矢量的坐标分量(或矢端点的坐标)就是这样的一组数。当坐标基矢变换时,它们却逆转而变,所以属于逆变张量。又因为它们的变换因子中只乘了一个矩阵,所以属于一阶张量。下面举例说明。
图:一阶逆变张量
通过前几回的讨论我们知道,当坐标变换时,两组基矢之间的变换关系体现为一个过渡矩阵A。仍以二维空间为例,假定可记为
或一般地对于n维空间写成
其中基矢变换矩阵(过渡矩阵)A为n×n阶方阵
一阶逆变张量的定义是说:当坐标基矢按如上矩阵A变换时,则矢量P的坐标分量却按矩阵B“逆转而变”成
对于二维空间中即
对于n维空间一般即
其中坐标变换矩阵B也是一个n×n的方阵
如果变换矩阵B恰是过渡矩阵A的转置逆矩阵
则这样的矢量(一组数)就属于逆变量,叫做一阶逆变张量。
注意:上式中矩阵元素的指标次序倒置表示矩阵的转置。
可见,张量是一组数,其中随坐标基矢变换“逆转而变”者属于逆变张量,变换因子中只乘一次矩阵者叫做一阶张量。矢量就是一阶张量的典型实例。
一阶张量的几何意义如上图。中国古代汉语中“张”字的本义是指把弦安装到弓上,拉的紧绷绷的。英语中“张量”一词tensor也是“拉紧”的意思。作为某个一阶张量的矢量实体,是个客观存在的不变量,但我们采用不同的坐标系来描述它时,却表现为不同的坐标分量组合,张成不同的平行四边形,然而两个平行四边形的对角线(矢量实体)始终不变,描述的对象是同一个“量”,这样的量就是张量。
值得提醒大家的是,矢量是一阶张量的典型实例,但一阶张量不仅仅只有矢量。况且上述举例的矢量是一阶逆变张量,只不过是一阶张量中的一类,实际中还存在一阶协变张量。究竟什么是一阶协变张量呢?且听下回分解。






















































































| 首页>>学科资源栏目>>学科教学资源>>高中物理>>物理博览>>大学物理(理论核心部分) | |
| | 加到收藏夹 添加相关资源 |
1.1 质点运动的描述
由于运动学的任务在于描写空间位置的改变,而不涉及物体相互作用和运动之间的关系.因此,我们重点讨论运动学中最为基本的质点的运动.本节介绍质点运动学的基本概念,着重讨论两个基本的物理量——速度和加速度.
1.1.1 质点
物体是研究对象的统称,实际物体总有其大小和形状,而且一般说来,它们在运动中可以同时有旋转、变形等等.但是,如果物体的大小和形状在所研究的问题中不起作用或作用很小,就可以忽略物体的大小和形状,而把物体抽象为只有质量的几何点,这样的研究对象在力学中称为质点,例如,当我们讨论地球公转问题时,并不涉及地球自转所引起的各部分运动的差别,地球的形状、大小无关紧要,因此可以把地球看作是一个质点.实际上所谓质点是一个从实际中抽象出来的理想模型,即具有质量的点.
应当指出,一个实际的研究对象能否看成是质点,不是依物体的大小而定,而是依问题的性质而定.如在有些问题中,大如恒星亦可视作质点,在另一些问题中小如分子、原子亦须考虑其形状、大小.还有,同一个物体在这个问题中可当作质点,在另一问题中却不能作为质点处理.总之,能否将物体视作质点,要根据问题的性质而定,要看把实际对象抽象为质点时是否能反映运动的主要特征.
质点是力学中最基本、最简单的理想模型,以后我们还将引入质点系等理想模型.掌握了质点的运动规律,就能用数学方法推导出质点系的运动规律,因此,研究质点的运动是研究更为复杂的运动的基础.实际上,在一定条件下,把实际研究对象抽象化、理想化为某种模型,这种研究方法在物理学中经常采用,它使我们能够把握住事物的主要方面,使我们对事物的认识更深刻、更正确、更全面.
1.1.2 参考系和坐标系
1.参考系
一切物体都在运动,即使看来“静止”的建筑物如房屋、桥梁等也正随着地球一起运动.地球不但自转,还围绕太阳公转;而太阳系相对于附近恒星说来,正朝着武仙星座运动;太阳又是银河系的成员,而银河系也在旋转着…….这些事实表明,运动是普遍的、绝对的,而“静止”只有相对的意义.
虽然运动具有绝对性,但是,对运动情况的具体描述则具有相对性.例如,在水平匀速前进的火车中,一乘客竖直向上抛出一个小球.车上乘客观察到这小球是沿直线运动,而地面上的人观察到的却是小球沿一条抛物线运动.这是因为车上乘客选择车厢为标准,而站台人员以地面为标准,从而得出不同结论.一个运动相对于不同的标准具有不同的运动描述,这就叫做运动描述的相对性.
由于机械运动具有相对性,因此,描述一个运动时,就必须选择其他物体作标准.描述运动时选作标准的物体(一个不变形的物体,或保持相对静止的几个物体),称为参考系.
在研究运动学问题时,参考系可以任意选择,看问题的性质和计算的方便而定.例如,描述太阳系行星运动时,如果使用太阳参考系,则行星作椭圆运动;但是,如果用地球参考系,它们将作复杂的曲线运动.因此,以太阳参考系描述行星的运动比较简单方便.而在描述地球上的物体运动时,常选择地球为参考系.
2.坐标系
参考系确定之后,要把质点在各个时刻相对于参考系的位置定量表示出来,还需要在参考系上固定一个坐标系,所讨论的这个质点的位置就由它在该坐标系中的坐标决定.因此,对于描述物体的位置变化来说,坐标系起着刻度尺的作用.
最常用的坐标系是直角坐标系,有时根据需要也可选用其他坐标系,如球坐标系、自然坐标等.
1.1.3 位置矢量 运动方程
1.位置矢量
要讨论质点位置随时间的变化,先要确切描述质点的位置.为了同时给出质点相对于参考点的距离和方位,可以引入位置矢量.由参考系上的坐标原点引向质点P所在位置的矢量称为质点的位置矢量.如图1-1所示,通常以r表示.
在国际单位制(SI)中,位置矢量大小的单位为米(m),与长度单位相同.

位置矢量可在直角坐标系Oxyz中用三个互相正交的分量来表示,如图1-1所示.若p点的位置矢量r在x,y,z轴上的分量(即坐标)分别为x,y,z,则位置矢量的正交分解式为
r=xi+yi+zk
(1.1)
式中i,j,k分别表示沿x,y,z轴正方向的单位矢量.x,y,z称做质点的位置坐标,也可用来描述质点的位置,与用位置矢量来描述是一致的.
位置矢量的大小(即r的模)为
位置矢量的方向,可由其方向余弦确定:

式中α,β,γ分别表示r与x,y,z轴正方向之间的夹角(取小于180°值),它们满足以下关系式:
cos2α+cos2β+cos2γ=1
故三个方向余弦中只有两个是独立的.
2.运动方程
在质点运动过程中,它的位置矢量随时间改变,每一时刻均有一定的位置矢量与之对应,如图1-2所示,即位置矢量r为时间t的函数
r=r(t)
上式称做质点的运动方程.它给出任意时刻质点的位置.下面讲了速度与加速度后,我们将看到,如已知质点的运动方程,就可以确定质点在任一时刻的速度和加速度,即掌握了质点运动的全部情况.因此,求出运动方程是质点运动学的中心问题.

运动方程在直角坐标系Oxyz中的正交分解式为
r=r(t)=x(t)i+y(t)j+z(t)k
(1.2)
质点运动时,坐标x,y,z都是时间t的函数,所以运动方程在直角坐标系中也可写成

(1.3)
称为质点运动方程的标量形式.
当质点被限制在一平面内运动,例如在xy平面内运动时,称为二维运动,其运动方程为
(1.4)
当质点被限制在一直线上,例如在x轴上运动时,称为一维运动,其运动方程为
x=x(t)
(1.5)
3.轨迹
质点在所选定的参考系中运动时,在空间所经过的路径称为质点运动的轨迹.随着质点的运动,其位置矢量的矢端也在空间运动,实际上,矢端的轨迹就是质点运动的轨迹,如图1-3所示.轨迹可用数学形式表示,以质点在平面上的运动为例,其运动方程为(1.4)式,消去t,得
y=y(x)
这就是质点在直角坐标系中的轨迹方程.实际上,式(1.3)也可以看作是以时间t为参数的质点轨迹的参数方程.

例1 已知一质点的运动方程为
r(t)=ati+(bt-ct2)j
a、b、c为常数,求该质点的轨迹.
解 该质点的运动方程在直角坐标系中的表达式为

所以它在xOy平面上运动,从第一式和第二式中消去t,便得
这就是该质点的轨迹方程,它是在xOy平面上的经过原点O的抛物线.
例2 已知一质点的运动方程为

式中时间和坐标值均采用国际单位制.求:
(1)t=2s和t=4s时质点的位置;
(2)质点的运动轨迹。
解 (1)质点在xOy平面上作二维运动.
t=2s时,

t=4s时
(2)由所给的运动方程消去时间t,得
x2+y2=25
这表明该质点的轨迹是以原点O为圆心,半径等于5m,在xOy平面上的圆.如图1-4所示.读者不难看出,质点是沿着顺时针方向作圆周运动.

1.1.4 速度
1.位移和路程
为了描述质点在一定时间间隔内位置的变动,我们引入位移矢量.参照图1-5,一运动着的质点,其位置在轨道上连续变化,设t时刻质点位于P点,t+△t时刻到达Q点,r(t)和r(t+△t)分别表示时刻t和t+△t的位置矢量.自质点初始位置引向△t时间后末位置的矢量△r称作质点在这段时间间隔内的位移.由图可以看出,位移也就等于质点在这段时间内位置矢量的增量:
△r=r(t+△t)-r(t)
(1.6)

写出△t始末的位置矢量在直角坐标系中的正交分解式:
r(t+△t)=x(t+△t)i+y(t+△t)j+z(t+△t)k
r(t)=x(t)i+y(t)j+(t)k
二式相减得位移
△r=[x(t+△t)-x(t)]i+[y(t+△t)-y(t)]j+[z(t+△t)-z(t)]k
=△xi+△yi+△zk
(1.7)
这是位移在直角坐标系中的正交分解式,它表明位移可由位置坐标的增量来决定.
应当指出,位移刻划出质点在一段时间内位置变动的总效果,但并未给出质点是沿什么路径由起点运动到终点的.因此一定要认清质点在一段时间内的位移△r和所经过的路程△s这二者的区别.就一般情况而言,位移并不表示质点在其轨迹上所走过路径的长度.例如长跑运动员绕400m跑道跑了25圈,他跑过的路程是10000m,但位移却是零!路程是在一段时间内,质点在其轨迹上经过的路径的总长度.位移是矢量,而路程是正的标量.一般说来,在同一时间间隔内,路程和位移的大小并不相等.
2.速度
为了描述质点运动的快慢和方向,我们引入速度这一物理量.
(1)平均速度
质点在t时刻到t+△t时刻这段时间内的位移是△r,我们可以用位移△r除以发生这段位移的时间△t,即单位时间内的位移△r/△t来近似地描述t时刻附近质点运动的快慢和方向.质点位移△r=r(t+△t)-r(t)与发生这一位移的时间间隔△t之比,称作质点在这段时间内的平均速度,记作v,
(1.8)
(2)瞬时速度
平均速度仅仅提供一段时间内位置总变动的方向和平均快慢,却不能精细地刻划质点在这段时间内发生的运动方向的改变和时快时慢的详细情况.显然,△t取得越短,近似的程度就越好,平均速度就越能反映出t时刻的真实运动情况.当△t→0,△r/△t趋近于一个确定的极限矢量,这个极限矢量确切地描述了质点在t时刻运动的快慢和方向,这就是质点在t时刻的瞬时速度,它等于t时刻至t+△t时刻一段时间内平均
(1.9)
即质点的瞬时速度等于位置矢量对时间的变化率或一阶层数,记作
(1.10)
速度的方向由位移△r的极限方向决定,当△t→0时,位移△r趋于轨道的切线方向.如图1-6所示.因此,质点在任一时刻的瞬时速度的方向和这个时刻质点所在处的轨道曲线相切并指向质点前进的方向。

此外,为了描述质点沿轨迹运动的平均快慢,又引入平均速率概念.质点经过的路程△s与经过这一段路程所用时间△t之比,称做这段时间的平均速率,用v表示,即
(1.11)
可见,平均速率是标量,它等于质点在单位时间内所通过的路程,因此平均速率和平均速度是两个不同的概念,只有当质点在直线上沿固定方向运动时,两者的量值才相等.
当△t→0时,弦长|△r|无限接近于对应的路程△s,故瞬时速率可以表示为
(1.12)
瞬时速率是标量,它反映质点在该时刻运动的快慢,其量值等于该时刻速度的大小.
速度和速率的单位同为米·秒-1(m·s-1).
(3)速度在直角坐标系中的表示
瞬时速度v在直角坐标系Oxyz中的正交分解式为
v=vxi+vyj+vzk
将(1.2)式对时间求导,得
(1.13)
与前式对比,得
即瞬时速度矢量的投影等于位置坐标对时间的一阶导数.vx,vy,vz为代数量,可取正值也可取负值.
瞬时速度的大小和方向余弦可表示如下:

例3 已知一质点沿x轴运动,其运动方程为
解 根据速度的定义,通过对质点的运动方程的徽分运算即可求出它的速度.
根据式(1.6),该质点的速度为

这个结果说明,质点的速度按正弦规律作周期性的变化,可正可负.若速度为正,则其方向沿x轴正方向;若速度为负,则其方向沿x轴负方向.所以,质点将在x轴上往复运动.这种按正弦或余弦规律的往复运动,叫作简谐振动.
1.1.5 加速度
质点运动时,瞬时速度大小和方向都可能变化,为了描述各个时刻速度矢量变化的情形,我们引入加速度的概念.
1.加速度
(1)平均加速度

设质点在t时刻的速度为v(t),经△t后速度变为v(t+△t),如图1-7所示,速度增量△v=v(t+△t)-v(t)与发生这一增量所用
(1.14)
平均加速度与一定时间间隔相对应,其大小反映△t时间内速度矢量的平均变化率,其方向沿着速度增量△v的方向.
(2)瞬时加速度
平均加速度只能近似地描述△t时间内速度变化的情况.显然,时间

称加速度,记作a.
(1.15)
即质点的瞬时加速度等于速度矢量对时间的变化率或一阶导数.又因
故得
(1.16)
即瞬时加速度等于位置矢量对时间的二阶导数.
加速度是矢量.加速度的方向为△v的极限方向,在一般情形下,△v的极限方向与速度v的方向并不一致,因而a的方向与v的方向不一致.例如在图1-8所示的斜抛运动中,质点在轨道上各点的速度都沿轨道切线方向,而加速度方向则总是向下的.从这个例子可以看出a的大致趋势:质点作曲线运动时,a的方向总是指向曲线凹的一侧.只有在质点的直线运动中,加速度的方向和速度的方向总是相同或相反.

加速度的大小,即
代表速度增量的大小随时间的变化率.值得提出的是,要正确理解加速度这一概念,必须注意它是与速度矢量增量△v密切相关的,因此,在运动过程中,不论速度的大小有改变或是速度的方向有改变,都是速度矢量有了变化。加速度都不等于零.例如,对匀速率曲线运动(例如匀速率圆周运动),虽然速度的大小保持不变,可是速度的方向不断变化,
在国际单位制中,加速度的单位是米/秒2(m·s-2).
2.加速度在直角坐标系中的表示式
将式(1.9)代入式(1.10),可得加速度在直角坐标系中的正交分解式

(1.17)
以ax,ay,az表示a在x,y,z轴上的投影:

(1.18)
即瞬时加速度在坐标轴上的投影等于位置坐标对时间的二阶导数.
由前面讨论得到了质点的位置矢量、速度和加速度在直角坐标系中的正交分解式.这些式子表明,任何一个曲线运动都可分解成为沿x,y,z三个方向的直线运动,每个方向上的运动是相互独立的,整个运动可看成是沿三个坐标轴直线运动的叠加,这就是运动的叠加原理.因为直线运动的描述最简单,每一个直线运动只需要用相应的坐标以及速度、加速度的投影就可以表示出来,所以利用直角坐标系可以把矢量问题化为较简单的标量问题处理.在分别研究了沿各个坐标轴方向的直线运动之后,整个运动可以由矢量叠加而求得.这样实际上对一般曲线运动的研究都可归结为对直线运动的研究.本节讨论的问题仅限于质点的二维或一维运动。
例4 如图1-9所示,已知物体由地面射出,其射出时相对于地面的速度为v0射角为θ0。,若不计空气阻力和风力等影响,试求:

(1)物体在任一时刻的速度和位置;
(2)到达最高点所需时间及最大飞行高度;
(3)由发射到落回地面所需时间和物体的射程;
(4)物体的运动轨迹.
解 建立直角坐标系Oxy,坐标原点在物体发射处,x轴滑水平方向,y轴竖直向上,发射物速度v0在Oxy平面内物体所作的抛体运动为平面运动(二维运动).如图1-9所示.
(1)物体飞行时的加速度为重力加速度g,故
ax=0,ay=-g.
对时间积分得

选择发射时为计时起点,则速度初始条件为
t=0,vox=v0cosθ0,voy=v0sinθ0
代入上式得任一时刻物体的速度为

计算vx和vy对时间的积分

根据以上计时起点和坐标系的选择,位置坐标的初始条件为
t=0,x0=y0=0
代入上式即得到任一时刻物体的坐标为

上式即为抛体运动方程的标量形式,也可写成矢量式
(2)设物体到达最高点所需的时间为tH,到达的最大高度为H,此时,速度的竖直分量为零,即vy=0,代入vy=v0sinθ0-gt,即得

的飞行总时间为
对应于y=0的另一个解t=0,表示物体在起点的时刻.
以T值代入x=v0cosθ0t,解得射程
(4)从函数x(t),y(t)中消去t,可以得到物体的轨迹方程
这就是真空中的弹道方程,表明物体飞行轨道是抛物线.上面的讨论没有考虑到空气阻力的影响,所得结论只有在空气阻力极小的情况下才比较符合实际.物体在空气中运动受到的阻力与物体本身的形状,空气的密度,特别是和物体的速率有关.物体速率越小,空气阻力的影响越小,抛体的运动越接近我们讨论的理想情况.
例5 已知一质点沿x轴运动,其位置矢量为
A、ω为常数,求该质点的加速度.
解 根据式(1.16),

前面在例3中已说过这种运动叫简谐振动.以上计算结果进一步说明,简谐振动的一个特点是,其加速度的方向与位量矢量的方向相反,加速度的大小与位置矢量的大小成正比.
3.切向加速度和法向加速度
质点运动的加速度,也可用自然坐标将a正交分解为切向加速度和法向加速度,如图1-10所示.如质点在A处,可在此处取一单位矢量沿切线方向,叫做切向单位矢量,记作τ,加速度沿此方向的投影称做切向加速度.另取一单位矢量沿曲线法线且指向曲线的凹侧,称做法向单位矢量,记作n,加速度沿此方向投影称做法向加速度.

我们首先就圆周运动讨论质点的法向加速度和切向加速度.然后推广至一般平面曲线运动.
质点作圆周运动,如图1-11所示.设在任一段时间内质点由P点运动到Q点,质点在这段时间内沿圆轨道所经过的路程即弧长为△s,它所对应的圆心角为θ,则
△s=Rθ
将上式代入式(1.12),可求得质点速度的大小,即速率等于

(1.19)
以,上式说明,质点作圆周运动时,其线速度等于圆周半径与其角速度的乘积.速度方向沿着运动轨迹在该点的切线并指向运动的前方.

质点作圆周运动时,如果其线速度的大小不随时间改变.则这种运动叫做匀速率圆周运动,否则就叫做变速率圆周运动.但是,不论质点运动的线速度的大小是否随时间改变,由于其速度矢量的方向总在不断地改变着,所以作圆周运动的质点的加速度不等于零.
现在先来讨论质点作匀速率圆周运动的加速度.
图1-12a中,设圆半径为R, t时刻质点位于P点,速度为v(t), t+△t时刻到达Q点,速度为v(t+△t).

为了计算出 a,可将矢量v(t)和v(t+△t)平移并画三角形 ABC,如图1-12b所示.因为v(t)重直于OP,v(t+△t)垂直于OQ,所以△t和v(t+△t)之间的夹角也是△θ,即在△t时间内速度方向转过了△θ角.可见,虽然速度大小不变,但因为速度的方向有变化,所以△v≠0.由加速度的定义式,t时刻(在P点)的加速度为
加速度的大小

故

因此加速度的大小为
(1.20)
由于v=ωR,代入上式,a又可以表示为
(1.21)
这就是说,在匀速率圆周运动中,质点的瞬时加速度的大小是一个

方向.于是,由上述得
(1.22)
由此可见,作匀速率圆周运动的质点具有指向圆心或沿法向单位矢
弯曲使速度方向发生变化引起的,是直线运动所没有的.
在变速率圆周运动中,质点速度的大小和方向都随时间改变,所以加速度a和速度v既不会象在直线运动中那样在同一直线上,也不会象在匀速率圆周运动中那样互相垂直,而是夹某一角度,如图1-13所示.这个夹角也可能随时间改变.
因此,在变速率圆周运动中,可将质点在任一时刻或质点在轨道上任一点的加速度正交分解为切向和法向两个分量,即
a=aτ+an
(1.23)
加速度的大小为
(1.24)
加速度的方向以a和该时刻的速度v之间的夹角α表示时,有
(1.25)

法向加速度an和向心加速度相同,它反映速度方向的变化率;切向加速度aτ反映质点速率(速度大小)的变化率,切向加速度可表示成
(1.26)
其大小为
(1.27)

这样,式(1.23)可写成
虽然以上结论是讨论圆周运动得到的,但也可应用到一般的曲线运动,因为一般曲线运动的每一小段都可看作是某一圆的一部分,只是不同小段所对应的圆半径不同而已,见图1-14.曲线上M点附近的一小段所对应的圆称为曲率圆,圆半径称为曲线在该处的曲率半径,用ρ表示.一般曲线运动的加速度可表示为

这种用法向分量和切向分量来表示加速度的方法叫作加速度在自然坐标中的表示法.
质点运动时,如果同时有法向加速度和切向加速度,则质点的速度大小和方向都改变.如果an=0,则a=aτ,质点作变速直线运动;如果aτ=0,则a=an,质点作匀速率曲线运动,若an只是方向改变而大小不变,即an=常量时,作匀速率圆周运动.因此,直线运动和匀速率圆周运动都是一般曲线运动的特例.
例6 列车出站时,由静止开始速率均匀增大,其轨道为半径R=800m的圆弧.已知离开车站一分钟时列车速率为24km·h-1(公里/小时),求在离开车站两分钟时的切向加速度、法向加速度和总加速度.
解 由于速率均匀增加,因此切向加速度大小不变,
已知在△t=1min内,速率增量△v=24km·h-1,故

欲求t=2min时的法向加速度an,应先求出这一时刻的速率v.因为初速为零,故
v=aτt.
t=2min时的法向加速度的大小

这一时刻的总加速度大小

a与v之间夹角

| |
李群、黎曼几何与纤维丛初探
Chern posted @ 2012年6月17日 01:04 in 数学物理 , 3859 阅读
李群、黎曼几何与纤维丛简介
由于量子力学与李群有关,广义相对论与黎曼几何有关,规范场与纤维丛有关,超弦与代数几何有关,所以物理学家要深入研究物理就必须对它们有所了解。在这篇文章中,我将对李群、黎曼几何与纤维丛做一个初步介绍(代数几何比较深奥,等我学完它的预备知识“交换代数与复分析”再说)。由于我是初学者,理解错误在所难免,所以外行请不要盲目相信,内行看出错误请指出来哪里错了,正确的理解是什么。就当我是抛砖引玉吧。
一、预备知识
1.切向量
设) 为一条光滑曲线,M、N为曲线上两点,坐标分别为
为一条光滑曲线,M、N为曲线上两点,坐标分别为 %3D x^i (t_0 )) ,
,
 %3D x^i (t_0 + \Delta t)) ,则曲线在M点的切向量就是N与M距离与Δt之比的极限:
,则曲线在M点的切向量就是N与M距离与Δt之比的极限:
 = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{x^i (t_0 %2B \Delta t) - x^i (t_0 )}}{{\Delta t}}\delta _i = \frac{{dx^i }}{{dt}}\delta _i)
为简化运算,上式使用了爱因斯坦求和约定,即重复出现的一对(上下)指标表示求和Σ.
但是,这样的定义依赖于欧式空间的线性结构。为了推广到一般的流形上去,我们必须给出另一种定义。我们假定读者已经熟悉流形的概念,不熟悉的可以看看我以前的拙作《现代微分几何的基本概念》。
设U为流形M上一个坐标邻域,p为U中一点。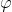 为M到
为M到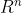 的光滑映射,它将U映为
的光滑映射,它将U映为) ,U中的p映为
,U中的p映为) 中的
中的) ,坐标为
,坐标为) . f为M上的光滑函数,即f为M到R的光滑映射,则从
. f为M上的光滑函数,即f为M到R的光滑映射,则从) 到R存在复合映射
到R存在复合映射 .
.
设γ: (- ε, ε) →M是光滑流形M中过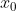 的一条光滑曲线,则从
的一条光滑曲线,则从) 到R存在复合映射
到R存在复合映射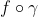 ,于是曲线γ确定了一个映射:
,于是曲线γ确定了一个映射:
 %3D \frac{d}{{dt}}(f \circ \gamma (t)) = \frac{d}{{dt}}(f \circ \varphi ^{ - 1} (x^i (t))))
} \cdot \frac{{dx^i }}{{dt}} = \frac{{dx^i }}{{dt}} \cdot \frac{\partial }{{\partial x^i }}(f))
即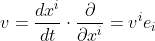
这说明任意向量v均可表示为 的线性组合,故
的线性组合,故 构成v空间的一组基,称为自然坐标基底。而
构成v空间的一组基,称为自然坐标基底。而 就相当于曲线的切向量v在自然坐标基底下的分量。可见,对于微分流形而言,切向量就等同于方向导数。
就相当于曲线的切向量v在自然坐标基底下的分量。可见,对于微分流形而言,切向量就等同于方向导数。
流形上某一点的所有切向量的集合称为该点的切空间,流形上所有切向量的集合称为切向量场。
2.诱导映射
设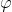 为流形M与N之间的映射,它将M中的x点映为N中的
为流形M与N之间的映射,它将M中的x点映为N中的) 点; f为光滑函数(N到R的光滑映射),它将N中的
点; f为光滑函数(N到R的光滑映射),它将N中的) 点映为R上的
点映为R上的) 点。则从x到
点。则从x到) 点可以定义映射
点可以定义映射 ,使得
,使得 %3D f \circ \varphi (x)) ,这样的映射
,这样的映射 就称为诱导映射。
就称为诱导映射。
除了流形之间可以定义可微映射,流形的切空间之间也可以定义诱导映射。
设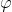 为流形M到N的映射,它将M中的x点映为N中的
为流形M到N的映射,它将M中的x点映为N中的) 点;f为N到R的映射;M的切空间到N的切空间的映射为
点;f为N到R的映射;M的切空间到N的切空间的映射为 %3D\varphi _ *) ,称为切映射,使得
,称为切映射,使得 %3D \varphi _ * (x) X(f)) ,如何确定
,如何确定 的具体形式(用
的具体形式(用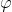 表达)呢?可以这样想:N中
表达)呢?可以这样想:N中) 经f映到R中一点,M中x经过
经f映到R中一点,M中x经过) 也映到R中同一点(因为
也映到R中同一点(因为) 是
是) 与f的复合映射,其总效果是将x映到R),所以N的切向量Y作用到f上与M的切向量作用到
与f的复合映射,其总效果是将x映到R),所以N的切向量Y作用到f上与M的切向量作用到) 上的效果是一样的,即
上的效果是一样的,即 %3D X(f \circ \varphi )) .又
.又 %3D \varphi _ * (x) X(f)) ,故
,故 X(f) %3D X(f \circ \varphi (x))) ,由于
,由于 %3D f \circ \varphi (x)) ,故有
,故有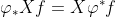 ,所以
,所以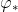 称为
称为 的对偶映射。
的对偶映射。
类似于切映射,还可定义余切空间(切空间的对偶空间)之间的余切映射。
设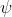 为流形N到M的映射,它将N中y点映为M中的
为流形N到M的映射,它将N中y点映为M中的) 点;g为M到R的映射;N的余切空间到M的余切空间的映射为
点;g为M到R的映射;N的余切空间到M的余切空间的映射为 %3D\psi ^ *) ,称为余切映射,使得
,称为余切映射,使得 %3D \psi ^ * (y) \theta (g)) ,如何确定
,如何确定 的具体形式(用
的具体形式(用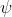 表达)呢?可以这样想:M中
表达)呢?可以这样想:M中) 经g映到R中一点,N中y经过
经g映到R中一点,N中y经过) 也映到R中同一点(因为
也映到R中同一点(因为) 是
是) 与g的复合映射,其总效果是将y映到R),所以M的余切向量ω作用到g上与N的余切向量θ作用到
与g的复合映射,其总效果是将y映到R),所以M的余切向量ω作用到g上与N的余切向量θ作用到) 上的效果是一样的,即
上的效果是一样的,即 %3D\theta (g \circ \psi )) . 又
. 又%3D \psi ^ *(y) \theta (g)) ,故
,故 \theta (g) %3D \theta (g \circ \psi (y))) ,由于
,由于 %3D g \circ \psi (y)) ,故有
,故有 ,所以
,所以 称为
称为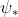 的对偶映射。
的对偶映射。
下面讲主丛上的联络时会用到余切映射这个结果,即_ *) .
.
注意,虽然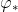 与
与 ,
, 与
与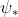 互为对偶映射,但
互为对偶映射,但 ,
, ,因为
,因为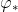 与
与 作用在切空间(向量场)上,而
作用在切空间(向量场)上,而 与
与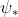 作用在余切空间(微分形式)上。
作用在余切空间(微分形式)上。
3.微分形式
微分形式我们已经在《微分形式与同调论浅析》中介绍过了。这里只是补充一个重要公式
dω(X,Y)=Xω(Y)-Yω(X)- ω([X,Y]),这个公式在李群的嘉当结构方程及黎曼几何的嘉当结构方程的证明中都是关键的一步。
为证明这个公式,我们先证明另一个重要公式df(X)=X(f). 设流形上的向量场为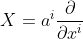 ,且
,且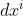 与
与 互为对偶:
互为对偶:
 %3D \frac{{\partial x^i }}{{\partial x^j }} = \delta _j^i)
 为克罗内克张量,当i=j时其值为1,当i与j不等时其值为零。
为克罗内克张量,当i=j时其值为1,当i与j不等时其值为零。
则
 %3D \frac{{\partial f}}{{\partial x^i }}dx^i (X) = \frac{{\partial f}}{{\partial x^i }}dx^i \left( {a^i \frac{\partial }{{\partial x^i }}} \right))
 = a^i \frac{\partial }{{\partial x^i }}f = X(f))
有了这个公式,就可以给出dω(X,Y)=Xω(Y)-Yω(X)- ω([X,Y])了。设有一次形式ω=fdg,其中f,g为函数(零次微分形式),则
dω(X,Y)=d(fdg)(X,Y)=(dfΛdg-fddg)(X,Y)=(dfΛdg)(X,Y)=df(X)dg(Y)-dg(X)df(Y)
=(Xf)(Yg)-(Xg)(Yf)=X(f(Yg))-Y(f(Xg))=X(f(Yg))-Y(f(Xg))-f(XYg-YXg)
=X(fdg(Y))-Y(fdg(X))-fdg(XY-YX)= Xω(Y)-Yω(X)-ω([X,Y])
4.向量场的积分曲线
既然每一根曲线在每一点都有一个切向量,那么是否任意给定一个向量场,就有可能从某一点P开始作出一条曲线,使该曲线上任意一点的切向量就是此向量场在这一点的向量?回答是,对于 向量场,这是可以的,我们把这种曲线称为该向量场的积分曲线。
向量场,这是可以的,我们把这种曲线称为该向量场的积分曲线。
该向量场的分量是) ,它是P的函数。在某一坐标系
,它是P的函数。在某一坐标系 中,有
中,有 %3D v^i (x^j )) 它是参数为λ的曲线的切向量,即
它是参数为λ的曲线的切向量,即) ,这正是
,这正是) 的一个一阶常微分方程组,它在初始点P的某个邻域中总存在一个唯一的解。因此,除
的一个一阶常微分方程组,它在初始点P的某个邻域中总存在一个唯一的解。因此,除 的点,不同积分曲线的路径是不会相交的。由于在每一点P总有一条积分曲线通过,因此积分曲线遍布M.这种遍布流形的曲线集合称为一个“线汇”。有时也把曲线的这一集合看做流形本身。
的点,不同积分曲线的路径是不会相交的。由于在每一点P总有一条积分曲线通过,因此积分曲线遍布M.这种遍布流形的曲线集合称为一个“线汇”。有时也把曲线的这一集合看做流形本身。
二、李群
1.李群
设G是一个非空集合,如果G是一个群,并且G还是一个光滑流形,则称G是一个李群。可见,李群集代数、几何性质于一身。
物理系的群论课程一般都会讲到李群的代数性质,但很少讲李群的几何方面,因为量子力学、量子场论的问题差不多都能在群论的框架下解决,而不必牵涉几何学;相对论对几何学依赖性比较大,但又不牵涉到群论。总之,群论的几何方面被一部分物理学家忽视了。然而,根据克莱因的观点,几何学与变换群密不可分。实际上,纤维丛就是这样一个既涉及流形、又涉及群的结构。本文最终是要定义主纤维丛上的联络,那么自然要在群论的几何方面多洒点笔墨。我们先简单回顾李群的代数性质,然后详细讲讲李群与微分几何的联系。
2.李代数
化难为易,把李群线性化,即寻找一个有限维的线性空间来近似代替它,通过对这个线性空间的深入研究来窥见李群的性质,便成为数学家的一个心愿。李代数就是这样一个线性空间。为了给出李代数的概念,先要定义李括号。
给定一个坐标系x^i ,那么用 作为向量场的基是很方便的。然而,向量场的任意线性无关集合都可以用来作基,并非所有基都能由坐标系得出。这是因为对所有的i和j,算子
作为向量场的基是很方便的。然而,向量场的任意线性无关集合都可以用来作基,并非所有基都能由坐标系得出。这是因为对所有的i和j,算子 与算子
与算子 是可交换的,但对任意两个向量场却不一定可交换。例如,对
是可交换的,但对任意两个向量场却不一定可交换。例如,对
 和
和 ,有
,有
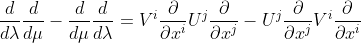
\frac{\partial }{{\partial x^j }})
所以,换位子(李括号)
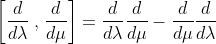
是一个非零向量场,它的分量一般不是零。
容易验证,李括号满足线性[aX+bY,Z]=a[X,Z]+b[Y,Z],反对易性[X,Y]+[Y,X]=0和雅克比恒等式[X,[Y,Z]]+[Y,[Z,X]]+[Z,[X,Y]]=0,故向量场关于李括号构成了一个李代数。李代数构成了量子力学的基础,例如角动量问题可以归结为求解SO(3)或SU(2)的李代数方程。一般的群论书在这方面讲的很详细,而且也很好理解,所以我就不再赘述了。下面开始讨论李群的几何方面。
3.李导数
在正式引出李群对几何的作用之前,先看看李群是怎么进入几何学的。
向量场的积分曲线汇给出了此流形到其自身中的一个自然映射。如果λ是这些曲线的参数,则任意足够小的数Δλ定义了一个映射,它把每一点映成线汇中同一根曲线上参数再增加Δλ的那一点。这种映射称为沿该线汇的一个“拉曳”。
有了拉曳的概念就使我们能沿着线汇定义导数。定义向量场和张量场导数的任何努力都有一个内在的困难.考虑一下,如果把向量场的导数定义为:不同点的向量之间的差除以这两点之间的距离,再取极限,那问题之一是如何去定义点之间的“距离”.如果这两点都在一根曲线上的话,则我们可以把这段距离取为这两点的参数值之间的差.(这就给出关于参数的导数,而在没有度规的流形上,能做到的就是这一点了.)更严重的问题是对不同点的向量的比较:不同点的两个向量“平行”与否,在欧几里得平面中,这是一个容易回答的简单问题.在弯曲的曲面上这一问题可能没有唯一的答案.在一个简单的可微流形上,在不同点的平行问题甚至是没有意义的,因为此时不存在标志或标尺,用以平行地移动向量.为了定义绝对平行,此时必须在流形上附加其他的结构,即所谓仿射联络,我们下面讲黎曼几何时再来研究这个问题.在这里我们将考虑另一种方法,它在线汇起主要作用的那些问题中是可用的.线汇本身能代替不同点平行的概念.也即当要比较同一曲线上位于点λ和λ+Δλ处得向量时,我们就可以把在λ+Δλ处得向量拉曳到λ处,这就在λ处定义了一个新向量,从λ处得原向量减去这个新向量就定义了两者之差。首先考虑一个标量函数f,求它在λ+Δλ的值,拉回到λ点,减去该标量函数在λ点的值,除以Δλ,并取极限Δλ→0.通过拉回映射我们定义了一个新标架场f*,它的值由df*/dλ=0定义,所以它在λ处的值与λ+Δλ处得值是一样的,即f*(λ)=f(λ+Δλ).于是Lv(f)=lim[f*(λ)-f(λ)]/ Δλ=lim[f(λ+Δλ)-f(λ)]=df/dλ.我们把Lv(f)称为f的李导数。
任意向量场由曲线的线汇所定义。设有两个线汇μ和λ,在d/dλ映射下,μ线汇的任意曲线映为一根新曲线,它是原来曲线上各点在李拉曳下的象构成的新点的集合,所形成的曲线就定义了参数为 的一个新的线汇,这个新线汇的切向量场为
的一个新的线汇,这个新线汇的切向量场为
 ,称为d/dμ在李拉曳下的象。
,称为d/dμ在李拉曳下的象。
向量场是用其对函数的作用来定义的。所以场U=d/dμ在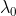 处给出导数
处给出导数
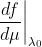 ,在
,在 处给出导数
处给出导数 ,将其拉曳
,将其拉曳) ,得新场U*=d/dμ*,则
,得新场U*=d/dμ*,则
f %3D \mathop {\lim }\limits_{\Delta \lambda \to 0} \frac{{U^ * (\lambda _0 ) - U(\lambda )}}{{\Delta \lambda }}f = \mathop {\lim }\limits_{\Delta \lambda \to 0} \frac{{\left( {\frac{d}{{d\mu ^ * }}f} \right)_{\lambda _0 } - \left( {\frac{d}{{d\mu }}f} \right)_{\lambda _0 } }}{{\Delta \lambda }})
由[U*,V]=0及 %3D U(\lambda _0 + \Delta \lambda )) 可得
可得

及
_{\lambda _0 %2B \Delta \lambda } %3D \left( {\frac{d}{{d\mu }}f} \right)_{\lambda _0 + \Delta \lambda })
则
_{\lambda _0 } %3D \left( {\frac{d}{{d\mu ^ * }}f} \right)_{\lambda _0 %2B \Delta \lambda } - \Delta \lambda \left[ {\frac{d}{{d\lambda }}\left( {\frac{d}{{d\mu ^ * }}f} \right)} \right]_{\lambda _0 } + o(\Delta \lambda ^2 ))
_{\lambda _0 %2B \Delta \lambda } - \Delta \lambda \left[ {\frac{d}{{d\mu ^ * }}\left( {\frac{d}{{d\lambda }}f} \right)} \right]_{\lambda _0 })
_{\lambda _0 } %2B \Delta \lambda \left[ {\frac{d}{{d\lambda }}\left( {\frac{d}{{d\mu }}f} \right)} \right]_{\lambda _0 } - \Delta \lambda \left[ {\frac{d}{{d\mu ^ * }}\left( {\frac{d}{{d\lambda }}f} \right)} \right]_{\lambda _0 })
于是
f %3D \mathop {\lim }\limits_{\Delta \lambda \to 0} \left( {\frac{d}{{d\lambda }}\frac{d}{{d\mu }}f - \frac{d}{{d\mu ^ * }}\frac{d}{{d\lambda }}f} \right))
由于μ*与μ只差Δλ的一次项,故可用d/dμ代替d/dμ*,于是
 %3D \frac{d}{{d\lambda }}\frac{d}{{d\mu }} - \frac{d}{{d\mu }}\frac{d}{{d\lambda }} = [V,U])
即两个向量场的李导数就是它们的李括号。而李括号构成李代数,所以李导数诱导了李代数。
4.李氏变换群
下面开始讨论李群对几何的作用。
设M是一个m维光滑流形,G是r维李群。若θ:M×G→M是光滑映射,记为θ(x,g)=x·g,使得对M中任意点x和G中任意元素g,h满足x·e=x,(x·g)·h=x·(g·h),则称G是右作用在M上的李氏变换群。类似地,若σ:G×M→M为σ(g,x)=g·x,满足e·x=x,g·(h·x)=(g·h)·x,则称G是左作用在M上的李氏变换群。
设G是右作用在M上的李氏变换群,若对G中任意一个非单位元素g,都有M中一点x,使得x·g≠x,则称G在M上的作用是有效的。特别地,若该变换为光滑同胚,则称G在M上的作用是自由的(或称G在M上的作用没有不动点)。
设G是左作用在M上的李氏变换群,若对于M中任意两点x,y,必有G中一个元素g使得y=g·x,则称G在M上的作用是可迁的。此时称M为齐性空间。令H={g ,满足 g·x=x},则H为G的闭子群,称为变换群G关于基点x的迷向群(亦称各向同性群)。
如果上述x不是M中的点,而是G中的元素,则把上述σ(g,x) 写成Lg(x),把θ(x,g)写成Rg(x),即Lg(x)=g·x , Rg(x)=x·g.由于Lg和Rg都是G到自身的光滑映射,由于 ,其中id为恒等映射,故
,其中id为恒等映射,故^{ - 1}) .同理
.同理^{ - 1}) .这意味着Lg和Rg有光滑的逆映射,故Lg和Rg为光滑同胚,分别称为李群G上的左移动和右移动。
.这意味着Lg和Rg有光滑的逆映射,故Lg和Rg为光滑同胚,分别称为李群G上的左移动和右移动。
设X为光滑切向量场中的一个切向量,若对G中任意g都有_ * X %3D X) ,则称X为李群G上的左不变向量场。在r为李群上全体左不变向量场构成一个r维向量空间,该空间中李括号是封闭的(即若X和Y为该空间的左不变向量场,则[X,Y]也是该空间的左不变向量场),因此该空间构成一个r维李代数,称为李群G的李代数。具体说来,设
,则称X为李群G上的左不变向量场。在r为李群上全体左不变向量场构成一个r维向量空间,该空间中李括号是封闭的(即若X和Y为该空间的左不变向量场,则[X,Y]也是该空间的左不变向量场),因此该空间构成一个r维李代数,称为李群G的李代数。具体说来,设 为该空间的一组基,
为该空间的一组基,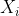 与
与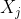 为该空间中任意两个左不变向量场,则
为该空间中任意两个左不变向量场,则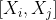 仍是该空间的左不变向量场,故可以表示成该空间中另一左不变向量场
仍是该空间的左不变向量场,故可以表示成该空间中另一左不变向量场 的线性组合,即
的线性组合,即 ,这就是著名的结构方程,其中,组合的系数
,这就是著名的结构方程,其中,组合的系数 称为李群的结构常数。我们利用李群定义了左移动,进而定义了左不变向量场,所以说李氏变换群诱导了左不变向量场;左移动就像前面定义李导数时所引入的李拉曳一样,所有的李拉曳变换构成一个变换群,即李氏变换群。由此可见,变换群诱导了向量场,向量场生成了变换群。
称为李群的结构常数。我们利用李群定义了左移动,进而定义了左不变向量场,所以说李氏变换群诱导了左不变向量场;左移动就像前面定义李导数时所引入的李拉曳一样,所有的李拉曳变换构成一个变换群,即李氏变换群。由此可见,变换群诱导了向量场,向量场生成了变换群。
设U是光滑流形M的一个开子集,若在U上每一点p都指定切空间TpM的一个h维子空间) ,则称
,则称 为U上的一个h维分布。如果属于该分布的任意两个切向量场
为U上的一个h维分布。如果属于该分布的任意两个切向量场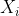 与
与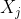 的李括号
的李括号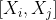 仍属于该分布,即
仍属于该分布,即 ,则称该分布是完全可积的。这就是著名的弗罗本尼斯定理,它给出了常微分方程组完全可积的条件(事实上,李群的基本理论就是Lie研究微分方程时给出的,但本文主要讨论李群与微分几何的关系,故不详细展开李群与微分方程的关系,感兴趣的读者可参阅相关书籍)。
,则称该分布是完全可积的。这就是著名的弗罗本尼斯定理,它给出了常微分方程组完全可积的条件(事实上,李群的基本理论就是Lie研究微分方程时给出的,但本文主要讨论李群与微分几何的关系,故不详细展开李群与微分方程的关系,感兴趣的读者可参阅相关书籍)。
我曾在《微分形式与同调论浅析》中介绍过微分形式,并且上面还补充了一个公式dω(X,Y)=Xω(Y)-Yω(X)- ω([X,Y]). 现在,我们就用它研究李群和黎曼几何。这一节先讨论李群上的微分形式,黎曼几何的微分形式在下面讲到活动标架法时再介绍。设ω为李群流形G上的一次微分形式,若(Lg)* ω=ω,则称ω为李群G上的左不变一次微分形式。与_ * X %3D X) 联立,可得
联立,可得
)g %3D \omega (g)X(g) = \omega (g)(L_g )_ * X(e))
^ * \omega (g)X(e) = \omega (e)X(e) = (\omega (X))e = const)
即ω(X)是G上的常值函数(下面讲纤维丛上联络的曲率时会用到这一结果)。
若ω为1次微分形式,则dω为2次微分形式。一般地,1次微分形式可写为ω=f(x)dx,2次微分形式可写为dx^i \wedge dx^j) .由外积的特点αΛβ= —βΛα,可以对上式进行反对称化,即
.由外积的特点αΛβ= —βΛα,可以对上式进行反对称化,即
dx^i \wedge dx^j %2B \frac{1}{2}f_{ji} (x)dx^j \wedge dx^i)
 - f_{ji} (x))dx^i \wedge dx^j)
设 ,
, ,
, ,则上式可简化为
,则上式可简化为 . 将dω用格拉斯曼空间Λ*(M)的基矢
. 将dω用格拉斯曼空间Λ*(M)的基矢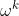 表示,即
表示,即
设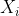 为Λ(M)的一组基,由于ω(X) 与ω(Y)为常数0或1(克罗内克δ张量),故公式dω(X,Y)=Xω(Y)-Yω(X)- ω([X,Y])简化为dω(X,Y)+ω([X,Y])=0
为Λ(M)的一组基,由于ω(X) 与ω(Y)为常数0或1(克罗内克δ张量),故公式dω(X,Y)=Xω(Y)-Yω(X)- ω([X,Y])简化为dω(X,Y)+ω([X,Y])=0
由于
 %3D \frac{1}{2}\gamma _{ij}^k \omega ^i \wedge \omega ^j (X_s ,X_t ))
} {\omega ^j (X_t )}- {\omega ^i (X_t )})
{\omega ^j (X_s )})
)
 = \gamma _{st}^k)
而 %3D \omega ^k (c_{st}^i X_i ) = c_{st}^i \omega ^k (X_i ) = c_{st}^i \delta _i^k = c_{st}^k)
于是 成为
成为
这就是著名的嘉当结构方程。这是李群的嘉当结构方程,后面我们还会谈到黎曼几何的嘉当结构方程、纤维丛的嘉当结构方程。
5.单参数变换群
假定我们有一个解析流形,同时假定向量场V=d/dλ的积分曲线上点的坐标为) 为λ的解析函数。于是,参数为λ和λ+ε的两个点的坐标由泰勒级数相联系:
为λ的解析函数。于是,参数为λ和λ+ε的两个点的坐标由泰勒级数相联系:
 %3D x^i (\lambda ) + \varepsilon \left( {\frac{{dx^i }}{{d\lambda }}} \right) + \frac{1}{{2!}}\varepsilon ^2 \left( {\frac{{d^2 x^i }}{{d\lambda ^2 }}} \right) + \cdots)
x^i = \exp \left( {\varepsilon \frac{d}{{d\lambda }}} \right)x^i)
所以,通过指数运算exp(εV ),我们把) 点映射为
点映射为) 点。εV是沿V的积分曲线的无穷小运动,它的指数运算exp(εV )给出一个有限转动。这与我们在高等量子力学中讨论有限转动算符的方法是一样的(参见:席夫《量子力学》,方励之 译)。
点。εV是沿V的积分曲线的无穷小运动,它的指数运算exp(εV )给出一个有限转动。这与我们在高等量子力学中讨论有限转动算符的方法是一样的(参见:席夫《量子力学》,方励之 译)。
考察过e的左不变向量场V的积分曲线,它在e处有唯一的切向量Ve,并且有唯一的参数t,当t=0对应e. 曲线上的点可用V的指数映射exp(tV)来定位。这正好包含由向量场V生成的变换群G到自身的微分同胚。不像一般的向量场,V完全由Ve确定,因此我们把G在此曲线上的点用 %3D \exp (tV)) 表示。根据指数运算性质
表示。根据指数运算性质\exp (t_1 V) %3D \exp [(t_1 %2B t_2 )V]) ,所以在这些积分曲线上的点构成一个群:
,所以在这些积分曲线上的点构成一个群:
 %3D \left. {\exp [(t_1 + t_2 )V]} \right|_e)
\exp (t_1 V)} \right|_e = g_{V_e } (t_2 )g_{V_e } (t_1 ))
这个群就称为G的单参数子群。这很简单,因为指数化乘为加,群乘法相当于参数值的加法。切空间中每一个向量都有唯一的一个子群;而且,因为每一个单参数子群都是G中通过e(子群总包括单位元素)的一根光滑曲线,所以在G的单参数子群与G的李代数元素之间有一个一一对应。
6.李群的伴随表示
李群和李代数的表示论已经成为一个非常深刻的专门理论,它在李群、李代数的结构理论,齐性空间、对称空间上的调和分析,泛函分析,微分几何以及物理学等各个方面有着广泛的应用,这里我们只介绍李群及其李代数的一种自然的、因而十分重要的表示,称为伴随表示,其表示空间是李群的李代数本身,它在我们下面定义纤维丛上的联络时起着关键的作用。
对于G中任意的g、h,定义映射ad(g):G→G如下: %3D ghg^{ - 1}) 即
即
 由此不难想到,当把g换成
由此不难想到,当把g换成 时,就有
时,就有
 %3D g^{ - 1} hg = L_{g^{ - 1} } R_g (h))
我们已经定义了Lg*ω=ω,很自然的问题便是,Rg*ω=?这就是我们在引入主丛联络时要讲的。实际上,它就是ω的伴随表示 ,即
,即 .这不难理解,如果ω与g可交换,那么
.这不难理解,如果ω与g可交换,那么 就变成
就变成 ,于是Rg*ω=ω.另一方面,联立Lg*ω=ω与
,于是Rg*ω=ω.另一方面,联立Lg*ω=ω与 ,可得
,可得 ,由ω任意性知
,由ω任意性知 ,再利用
,再利用^{ - 1}) 就得到
就得到 ,这个有点像厄米算符<Fφ, ψ>=<φ,Fψ>,其中*就相当于F,而φ、ψ分别类似于R、L. 当然,由上式也可以导出
,这个有点像厄米算符<Fφ, ψ>=<φ,Fψ>,其中*就相当于F,而φ、ψ分别类似于R、L. 当然,由上式也可以导出 .
.
如果说满足Lg*ω=ω的ω为左不变微分形式,那么满足Rg*ω=ω的ω就可以叫做右不变微分形式。同时满足左不变和右不变的ω就可以称为双不变微分形式。呵呵,上帝是个左撇子,对左不变比较偏爱,所以历史上并不曾有人定义右不变向量场和右不变微分形式,虽然有人定义了双不变,但那是指李群的双不变黎曼度量,即_ * X_y ,(L_x )_ * Y_y ) %3D g_y (X_y ,Y_y )) ,
,_ * X_x ,(R_y )_ * Y_x ) %3D g_y (X_x ,Y_x )) ,而不是双不变微分形式。
,而不是双不变微分形式。
设F是李群(流形)M到李群(流形)N的同态(映射),满足 %3D ghg^{ - 1}) ,则对于M的单参数子群exp(tX),有F(exp(tX))=exp(tY);根据前面关于切映射的讨论,N的切向量场Y与M的切向量场X之间满足Y=dF(X),故F(exp(tX))=exp(tY)= exp(tdF(X)).切映射是一种普遍的情形,当我们从一般到特殊时,dF就变成Ad.设d(Ad)记作ad,即ad=F,由此可证明(参见黄宣国《李群基础》),adX(Y)=[X,Y],ad[X,Y](Z)=[adX,adY](Z).即利用指数映射,通过伴随表示给出了李括号。我们前面曾利用李拉曳,通过李导数给出了李括号。实际上,还可以通过单参数变换群定义李导数(或通过单参数变换群定义伴随表示)来给出李括号(参见陈维桓《微分流形初步》)。这些不同的定义是等价的,因为李拉曳是一种特殊的指数映射,而指数映射生成了单参数变换群,伴随表示又是通过左右移动定义的。数学家要细致研究各种定义,物理学家只要掌握一种定义就够了,所以这里就不再赘述了。
,则对于M的单参数子群exp(tX),有F(exp(tX))=exp(tY);根据前面关于切映射的讨论,N的切向量场Y与M的切向量场X之间满足Y=dF(X),故F(exp(tX))=exp(tY)= exp(tdF(X)).切映射是一种普遍的情形,当我们从一般到特殊时,dF就变成Ad.设d(Ad)记作ad,即ad=F,由此可证明(参见黄宣国《李群基础》),adX(Y)=[X,Y],ad[X,Y](Z)=[adX,adY](Z).即利用指数映射,通过伴随表示给出了李括号。我们前面曾利用李拉曳,通过李导数给出了李括号。实际上,还可以通过单参数变换群定义李导数(或通过单参数变换群定义伴随表示)来给出李括号(参见陈维桓《微分流形初步》)。这些不同的定义是等价的,因为李拉曳是一种特殊的指数映射,而指数映射生成了单参数变换群,伴随表示又是通过左右移动定义的。数学家要细致研究各种定义,物理学家只要掌握一种定义就够了,所以这里就不再赘述了。
唉,一个通宵就写了这么点,太累了,剩下的下午再写吧。先把提纲列出来:
三、黎曼几何
弯曲空间中最重要的概念是曲率,要给出曲率必须先定义导数。但是,我们通常熟悉的长度、角度等与度规有关的几何概念,在流形中是没有的,它们不是流形的内禀性质,也不可能在流形的微分结构中自然产生。要定义导数,必须在流形上附加新的结构。前面定义的李导数是一种附加结构(线汇),这里我们给出另一种附加结构——联络。确切地说,就是通过曲面上的平行移动定义列维-奇维塔联络。弯曲空间的平行移动和列维-奇维塔联络在拙作《现代微分几何的基本概念》中已经介绍过了,这里不再重复。这里来讲讲比较现代的活动标架法和公理化方法。当然,为了照顾初学者,让我们从欧式空间的曲线坐标讲起。这是通常张量分析的内容,熟悉张量分析(主要是张量的协变导数)的读者可以跳过曲线坐标这一节,直接进入活动标架法。
1.曲线坐标
假定在欧式空间 中取定单位正交标架
中取定单位正交标架 ,相应直角坐标为
,相应直角坐标为) ,U为该欧式空间的开集,局部坐标为
,U为该欧式空间的开集,局部坐标为.) 若
若 是光滑同胚,即它在区域V上给出曲线坐标系
是光滑同胚,即它在区域V上给出曲线坐标系) ,坐标变换为
,坐标变换为
) . 则
. 则 曲线(
曲线( 变动,i≠j的
变动,i≠j的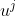 固定不动所得的曲线)的切向量是
固定不动所得的曲线)的切向量是 ,V中任意一点Q处得切向量
,V中任意一点Q处得切向量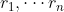 是线性无关的,因而
是线性无关的,因而 是欧式空间中Q点的一个标架,称为曲线坐标系诱导的自然标架。
是欧式空间中Q点的一个标架,称为曲线坐标系诱导的自然标架。
因为在不同点的自然标架不是互相平行的,所以计算它从一点过渡到邻近点的变差就很重要,特别是自然标架场沿坐标曲线的微商。设v,w是定义在区域V上的两个向量场,用自然标架表示为 ,注意到切向量
,注意到切向量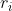 是
是 的函数,它关于
的函数,它关于 的导数仍是区域V上的向量场,因而可以看做V上向量r_k的线性组合,即
的导数仍是区域V上的向量场,因而可以看做V上向量r_k的线性组合,即 . 于是
. 于是
r_i)
即
r_i = \left( {dv^i + v^k \Gamma _{kl}^i du^l } \right)r_i)
设l(t)为一条光滑曲线,t为该曲线的参数(当该参数t选为弧长s时,该曲线就称为测地线)。设l(t)上每点的切向量为 ,沿曲线l(t)的向量场记为
,沿曲线l(t)的向量场记为 %3D v^i (t)r_i = v^i (t)\frac{\partial }{{\partial u^i }}) ,则
,则
\frac{\partial }{{\partial u^i }})
如果 ,就称为向量沿曲线的平行移动。
,就称为向量沿曲线的平行移动。
将参数t改成弧长s,此时平行移动的方程称为测地线方程。上述方程可以写成
v^i %3D 0)
有点像薛定谔方程\Psi %3D 0)
有人说薛定谔方程是一种特殊的测地线方程,但各项的物理意义是什么我不清楚。尤其是,为什么哈密顿量为 ?
?
我们讨论了半天 ,还不知
,还不知 的具体形式。下面我们就试着求出
的具体形式。下面我们就试着求出 的显示表达式。设w是定义在区域V上的另一个向量场,用自然标架表示为
的显示表达式。设w是定义在区域V上的另一个向量场,用自然标架表示为 ,那么v和w的内积为
,那么v和w的内积为 ,其中
,其中 . 于是
. 于是 . 于是
. 于是
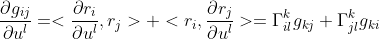
同理可得 和
和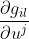 .
.
假定二阶混合偏导与次序无关,即
 ,则
,则 ,即
,即 .
.
由此可推导出
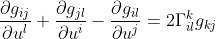
令^{ - 1}) ,则
,则
)
我们把 称为克里斯托菲符号,它其实就是《现代微分几何的基本概念》中引入的联络系数。
称为克里斯托菲符号,它其实就是《现代微分几何的基本概念》中引入的联络系数。 称为黎曼度量,引入了黎曼度量的流形就称为黎曼流形,(古典)黎曼几何就是研究黎曼流形性质的几何学。从上面的讨论可见,联络系数是由黎曼度量定义的,称为由黎曼度量诱导的黎曼联络。
称为黎曼度量,引入了黎曼度量的流形就称为黎曼流形,(古典)黎曼几何就是研究黎曼流形性质的几何学。从上面的讨论可见,联络系数是由黎曼度量定义的,称为由黎曼度量诱导的黎曼联络。
2.活动标架法
为了容易理解,在正式给出活动标架法之前,先看看大部分读者比较熟悉的仿射空间(定义了仿射坐标系,即斜角坐标系的欧式空间)上的微分形式。
设A³是一个3维仿射空间,它的一个标架是指A³中一点P及其与之相伴的向量空间(伴随向量空间)V的一个基底 组成的复合体
组成的复合体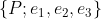 . A³中全体标架的集合记作
. A³中全体标架的集合记作 . 根据仿射空间的定义,对于每一个
. 根据仿射空间的定义,对于每一个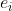 ,存在唯一的一点
,存在唯一的一点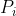 ,使得
,使得 ,所以标架
,所以标架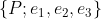 可以看作A³中以P为顶点的三棱形
可以看作A³中以P为顶点的三棱形 .
.
在标架空间 中取定一个元素
中取定一个元素 ,则A³中任意一个标架
,则A³中任意一个标架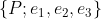 可表示为:
可表示为:




横看成岭侧成峰。从标架空间 看,dP,
看,dP, 无非是
无非是 ,它们给出
,它们给出 上余切标架场;但从仿射空间A³角度看,dP,
上余切标架场;但从仿射空间A³角度看,dP, 是A³中的切向量,它们能用基底
是A³中的切向量,它们能用基底 表示出来:
表示出来:




即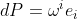 ,
, ,其中ω是
,其中ω是 上的一次微分形式。
上的一次微分形式。
对上式求外微分,得
 %3D d(\omega ^i e_i ) = d\omega ^i \wedge e_i %2B ( - 1)^1 \omega ^i \wedge de_i)
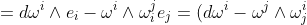e_i)
 %3D d(\omega _i^j e_j ) = d\omega _i^j \wedge e_j - \omega _i^j \wedge de_j)
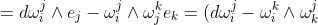e_j)
由于 ,故上式成为
,故上式成为


这就是仿射空间的结构方程。
考虑曲线坐标) ,
,\delta _i) ,令
,令
 ,
, ,前面讲曲线坐标时已经推出
,前面讲曲线坐标时已经推出
 ,故
,故 . 与
. 与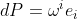 及
及 相比,可令
相比,可令 ,
,
 . 根据前面在微分形式中所讲的反对称化,有
. 根据前面在微分形式中所讲的反对称化,有
du^j \wedge du^k)

du^l \wedge du^k)
定义


 和
和 就是通常张量分析课程中所讲的挠率张量和曲率张量。
就是通常张量分析课程中所讲的挠率张量和曲率张量。
故


意味着挠率和曲率为零,这是平直空间的基本特征。对于弯曲空间,曲率一般不为零;并且,有时候挠率也不为零。与前面对曲线坐标的讨论对比可知,二阶混合偏导为零时联络是对称的,挠率为零。
推而广之,可以定义挠率形式和曲率形式为:
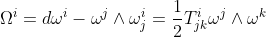
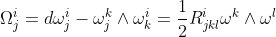
利用前面证明的公式dω(X,Y)=Xω(Y)-Yω(X)- ω([X,Y])
及外积定义
 %3D {\alpha (X)} {\beta (Y)}- {\alpha (Y)} {\beta (X)})
设 ,则在局部坐标下,上面定义的挠率和曲率形式化为:
,则在局部坐标下,上面定义的挠率和曲率形式化为:
 %3D d\omega ^i - \omega ^j \wedge \omega _j^i)
 - \omega ^j \wedge \omega _j^i (e_m ,e_n ))
) - e_n (\omega ^i (e_m )) - \omega ^i ([e_m ,e_n ]))
\omega _j^i (e_n ) - \omega ^j (e_n )\omega _j^i (e_m )))
 - e_n (\delta _m^i ) - \omega ^i ([e_m ,e_n ]) - \delta _m^j \Gamma _{jn}^i %2B \delta _n^j \Gamma _{jm}^i)
 - \Gamma _{mn}^i %2B \Gamma _{nm}^i)
 %2B \Gamma _{nm}^i \omega ^i (e_i ))
 - \omega ^i (\Gamma _{mn}^i e_i ) %2B \omega ^i (\Gamma _{nm}^i e_i ))
 - \omega ^i (\nabla _{e_n } e_m ) %2B \omega ^i (\nabla _{e_m } e_n ))
)
由此可定义 %3D \nabla _{e_m } e_n - \nabla _{e_n } e_m - [e_m ,e_n ]) ,使得
,使得
) %3D T_{mn}^i = \Omega ^i (e_m ,e_n )) ,这就是下面要讲的公理化定义。同样地,利用
,这就是下面要讲的公理化定义。同样地,利用
e_i %3D \omega ^h ([e_k ,e_l ])\Gamma _{jh}^i e_i)
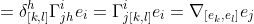
则对于曲率形式有
e_i %3D (d\omega _j^i - \omega _j^h \wedge \omega _h^i )(e_k ,e_l )e_i)
e_j)
并定义 %3D \nabla _{e_k } \nabla _{e_l } - \nabla _{e_l } \nabla _{e_k } - \nabla _{[e_k ,e_l ]}) .
.
3.公理化
前面已经提到,挠率和曲率可以不必依赖于空间的度量性质,而定义为
 %3D \nabla _{e_m } e_n - \nabla _{e_n } e_m - [e_m ,e_n ])
 %3D \nabla _{e_k } \nabla _{e_l } - \nabla _{e_l } \nabla _{e_k } - \nabla _{[e_k ,e_l ]})
事实上,按量子力学的看法,所有算子都是一种变换,作用在一个函数上给出另一个函数。所以,曲率、挠率乃至协变导数等其实都可以定义为一种映射(集合之间的变换)。算子本身可以看做附加在流形上的一种结构,而不必要求这种结构是从黎曼度量张量诱导出来的。下面我们就来介绍公理化方法。
设M是一个光滑流形,若有一个映射▽,对于任意向量场X,Y,Z和函数f均有:
(1) %3D \nabla _X Y + \nabla _X Z)
(2) %3D f \cdot \nabla _X Y %2B X(f) \cdot Y)
(3)
(4)
则称▽为光滑流形M上的一个联络。
之所以能公理化,是因为联络是不依赖于度量的;之所以要公理化,是为了运算简洁和符号美观。例如,设 ,
, ,
,

则
 = X^j \nabla _{\frac{\partial }{{\partial x^j }}} \left( {Y^i \frac{\partial }{{\partial x^i }}} \right))
 = X^j \left( {\frac{{\partial Y_i }}{{\partial x^j }} + Y^k \Gamma _{kj}^i } \right)\frac{\partial }{{\partial x^i }})
这是黎曼几何最美的公式之一,要问如何三步写出测地线方程?呵呵,除此之外,别无捷径。
黎曼几何还有许多美丽的公式,比如:
挠率 %3D \nabla _X Y - \nabla _Y X - [X,Y]) 或T=dθ-ω∧θ
或T=dθ-ω∧θ
曲率 %3D [\nabla _X ,\nabla _Y ] - \nabla _{[X,Y]}) 或R=dω-ω∧ω
或R=dω-ω∧ω
黎曼几何基本定理
比安基恒等式R(X,Y)Z+R(Y,Z)X+R(Z,X)Y=0或R∧θ=0
▽R(X,Y,Z,W,T)+▽R(X,Y,W,T,Z)+▽R(X,Y,T,Z,W)=0或dR=ω∧R-R∧ω
4.爱因斯坦方程
下面我们简单介绍下爱因斯坦的引力场方程。我们已经定义了曲率张量,它是一个逆变指标(上标)和三个协变指标(下标)的四阶张量。利用协变黎曼度量张量(二阶),可以把上标降下来(逆变度量张量将下标升上去),得到四个协变指标的四阶张量。根据张量运算规律,如果有一对(一上一下)指标相同,则约定求和,为哑标。所以,逆变度量张量与曲率张量的协变指标有两对相同时,通过缩并(有的书称为求迹,即矩阵元之和)运算就可以将四阶曲率张量变成一个二阶的新张量,这个新张量称为里奇张量。用同样办法将里奇张量再缩并一次,就得到一个标量,称为曲率标量R. 用二阶逆变曲率张量R^(μυ)减去逆变度量张量g^(μυ)与曲率标量R之积的一半定义了一个二阶对称张量G^(μυ),称为爱因斯坦张量。则G^(μυ)=KT^(μυ)就是引力场方程,其中K=-8πG/(c)^4为常数,T^(μυ)为能量动量张量。
如果粒子受到力的作用,则粒子运动的轨道就不是R³中的短程线了。更精确地说,如果我们坚持从平直空间的几何来看问题。则受力作用的粒子在该空间中就不是直线了.但是,我们也可从另一个角度来看问题,即把力几何化,认为现在空间不再是平直空间.而粒子运动轨道是这一新的几何中的短程线.
略为认真考虑一下,我们就会发现,力的几何化使我们必须从3维几何转到4维的几何上去。这一点可以阐明如下:例如我们在地面上的同一地点、以同样的角度而两种不同的速率发射两颗子弹,它们在地球引力的作用下显然将沿不同的轨道运动.现在,我们试图把引力场几何化,而给予3维空间某种新的结构,这样做是否能使这两条轨道都是该3维几何学中的短程线呢?仔细分析一下。就可以知道这是不行的,这是因为上述两条不同的轨道。出发于同一点,且在该点有相同的切线,所以如果它们是该3维几何中的短程线,则它们将是重合的,这就矛盾了.因此这一问题的出路是把时间放到我们的几何中来。引力的几何化使这个4维空间有了一个弯曲的结构,即黎曼曲率张量不为零。而这两条轨道现在都是该4维儿何中的短程线。现在。这是可能的,因为这两颗子弹的初速度是不同的.在此4维空间中,在开始时刻也不再是相切的了。可以各自成为一条短程线.以上正是广义相对论的基本思想之一。
把这种思想梢加引伸,我们也可以再考虑电磁力的几何化问题,举个简单的例子就会使我们看出解决问题的出路了.我们把上面的例子再扩展一些,假定地球是带正电的,那么在地球上同一点以同样速度发射各带正电和负电的两颗子弹,我们在R3中会得到两条不同的轨道。为了要使它们都是短程线,则原有的4维几何又待“改进了”.此时,我们要再加“电磁”这一维,才能使电磁力也几何化,这正是卡鲁扎-克莱因在本世纪二十年代提出引力和电磁力统一的理论思想,目前已成为一个广为研究的理论.我们下面就讨论它们的数学基础-一一纤维丛理论.
四、纤维丛
1.纤维丛
我们已经在《现代微分几何的基本概念》中介绍过切丛,即流形M与它在每一点的切空间T所构成的乘积流形TM. 下面我们介绍其他类型的纤维丛。
切空间是向量构成的集合,它的对偶空间称为余切空间,是由微分形式构成的集合。类似于切丛,可以把流形M与它的余切空间T*黏在一起定义,所得到的积流形T*M就称为余切丛。由于向量和微分形式都是张量的一种特殊情况(向量是具有一个上标的逆变张量,微分形式是具有一个下标的协变张量,一般的张量同时具有上下标),所以自然有张量丛的概念,而切丛和余切丛都是它的特例。
一般地,我们把上述积流形(即纤维丛)称为丛空间E(或全空间),M称为底流形(或底空间),而把切空间称为纤维型(或纤维空间)F. 由丛空间到底空间有投影映射(也称拉回映射)π,称为丛投影;由底空间到丛空间有推进映射s,并把满足复合映射π·s=id(id为恒等映射)的s称为纤维丛的截面。一般的纤维丛还包含结构群G,它作用于丛空间,从纤维上一点移到另一点,移动方法就是李群的左右移动。当纤维空间F为向量空间时,E就称为向量丛;当纤维空间F与结构群G相等(同构)时,E就称为主丛(为避免混淆,主丛记作P);把流形M上x点的切空间的一组有序基称为M的一个标架,x点及其这些标架构成的集合称为M上的线性标架主丛,简称线丛,记作L(M),其结构群为一般线性群GL(n,R),即所有n×n矩阵构成的集合。每个主丛P都有一个与之相伴的纤维丛E=(P×F)/G,称为伴丛,例如流形上的切丛就是线丛的伴丛。
我们曾比较过柱面与莫比乌斯带,前者是圆周与R的直积,后者不是直积。我们称满足直积的丛为平凡丛,不满足就称为非平凡丛。一般的纤维丛大多是非平凡丛。就像流形M局部同胚于欧式空间一样,虽然一个纤维丛整体上是非平凡的,不存在整体截面,但局部上是直积空间,这就导致局部平凡化和局部截面的概念。不同的纤维之间是无关的,为了联系它们,就要定义转移函数(也称变换函数)。转移函数的集合称为转移函数族,它正是纤维丛E的结构群G,在构造纤维丛时起着关键的作用。
在这里要强调一点:Do mathematics by picture!这个思想是阿诺尔德《经典力学的数学方法》讲的。关于映射最好的理解方法就是作图,这些抽象的逻辑推理一旦用图形画出来就变得非常简单。比如前面讲切向量的公理化定义,还有诱导切映射和余切映射,用图形思考就比用逻辑推理简单得多。这里也一样。考虑一个向量丛E. 我们可以建立一个平面直角坐标系,x轴表示底空间M,y轴表示向量空间(纤维空间)F,那么xy平面就是丛空间E. 于是x轴上的一个区间U就表示M的一个局域,x轴上一点m表示M上一点,y轴上一点n表示F中一点,xy平面内一点(m,n)表示E中一点。那么,什么是局部平凡化呢?什么是转移函数呢?就是在x轴上取区间U1与U2,假定交集非空,q为交集中一点,投影π将xy平面内一点(m,n)映射为x轴上一点m,π的逆映射π^(-1)将q点沿x=q提升到平面内(q,n)点,将区间U映射为y=n直线上的一个线段L. 设ψ为U×F到L的映射,U×F就是局部平凡化,即全空间局部上是底空间局域与纤维空间的乘积;ψ^(-1)为从L到U×F的映射。于是,ψ1为U1×F到L1的映射,ψ2为U2×F到L2的映射,(ψ2)^(-1)与ψ1的复合映射g=(ψ2)^(-1)·ψ1(q)将U1与U2交集中x=q上(q,0)点与(q,n)点之间的线段(q点处一根纤维)映射为(q,n)点,然后又将(q,n)点映射为(q,0)点与(q,n)点之间的线段(q点处一根纤维),总体效果是从一根纤维映射到一根纤维,所以复合映射g12就是上面所说的转移函数。纤维空间是向量空间,纤维之间的变换就像向量之间的变换矩阵(如我们早就熟悉的,两个向量之间通过二阶张量相联系)。所有变换矩阵g12构成一个群,它就是向量丛的结构群。
2.纤维丛上的联络
我们只介绍主丛上的联络,这个对于理论物理最为重要。一般纤维丛的联络可类似定义,有兴趣读者可参考相关书籍。
黎曼联络可以公理化,主丛联络也可以:主丛P(M,G)上的一个联络是一个线性映射,即对P中任意点p,M中任意点x,π(p)=x,[π^(-1)]x=Fx满足dπ·Γp=idTx(M)和
_ * \Gamma _p) ,Rg为李群上的右移动,dRg为Rg的切映射(或称推进映射)。
,Rg为李群上的右移动,dRg为Rg的切映射(或称推进映射)。
设切空间Tp(Fx)=Vp是切于纤维Fx的向量空间,称为竖直子空间(或垂直子空间),则主丛P中的联络Γ是对P中每个p点指定一个切空间Tp的水平子空间Hp,使得切空间分解为Tp=Hp+Vp,切映射满足dRgHp=Hpg. 对于M中每个向量场X,在P中都存在唯一的向量场 ,称为X的水平提升。
,称为X的水平提升。
任取P上的光滑向量场X,在P中每点p,X可分解为X=vX+hX,其中vX和hX分别称为X的竖直分量和水平分量。竖直分量恒为零的向量场称为水平向量场,水平分量恒为零的向量场称为竖直向量场。在P(M,G)上给定一个联络Γ,则在P上存在一个g值(g代表结构群G的李代数)一次形式ω,称为联络形式,满足
(1)ω(X)=vX,即若X属于水平子空间Hp,则ω(X)=0
(2) %3D R_g^ * \omega (X) = ad_{g^{ - 1} } \omega (X))
我们不做证明,只说明一下。第一条中的ω(X)为常数,这在讲微分形式中证明过;第二条中前一个等式我们在余切映射中讲过,后一个等式在李群的伴随表示中讲过。对证明感兴趣的读者可参阅陈维桓《黎曼几何引论》(下)。
3.联络的曲率
设P(M,G)为主丛,Γ为其中一个联络。考虑P上的一个与Γ相伴的p次形式ω,它在有限维向量空间中取值,则我们可以定义一个p+1次形式Ω=▽ω,它是一个g值(g为李代数)2次形式,称为联络的曲率形式(也称为称为外协变微分或外协变导数),为
 %3D d\omega (hX, \cdots ,hX_{p + 1} ))
简写为Ω=▽ω=dω·h. 其中X为P上光滑向量场,d为外微分,h为主丛P的切空间Tp到它的水平子空间Hp的投影(所以,如果这些X中有一个是竖直的,则▽ω=0)。这个曲率2次形式满足
(1)嘉当结构方程Ω(X,Y)=dω(X,Y)+[ω(X),ω(Y)]
(2)比安基恒等式▽Ω(X,Y,Z)=0.
证明:(1)将向量场分解为水平分量和竖直分量,分类讨论:
①X,Y都是水平的,则ω(X)=ω(Y)=0,于是嘉当方程化为Ω=dω,这正是Ω的定义;
②X,Y都是竖直的,则Ω(X,Y)=0(前面说了,这些X中有一个是竖直的,则▽ω=0),故只需证明dω(X,Y)+[ω(X),ω(Y)]=0;另外,前面讲微分形式时说过,ω(X), ω(Y)为常数,由于X,Y为切向量,而切向量等同于方向导数,故X(ω(Y))=Y(ω(X))=0;前面讲微分形式时证明了一个重要公式,即dω(X,Y)=Xω(Y)-Yω(X)-ω([X,Y]),故dω(X,Y)+[ω(X),ω(Y)]= dω(X,Y)+ω([X,Y])=Xω(Y)-Yω(X)=0-0=0=Ω(X,Y),所以嘉当方程成立
③X为竖直的,Y为水平的,则与②类似仍有Ω(X,Y)=0(X中有一个是竖直的则▽ω=0),故只需证明dω(X,Y)+[ω(X),ω(Y)]=0,结合dω(X,Y)=Xω(Y)-Yω(X)-ω([X,Y]),即只需证明Xω(Y)-Yω(X)-ω([X,Y]) +[ω(X),ω(Y)]=0;且Y为水平的使得ω(Y)=0,X为竖直的使得ω(X)为常数,从而Yω(X)=0,故只需证明ω([X,Y])=0. 下面我们就来证明。设φ(t)是由X生成的单参数子群,由于Y是水平的,故右移动的推进映射 也是水平的,从而X与Y李括号
也是水平的,从而X与Y李括号
是水平的,于是有ω([X,Y])=0.
注:有的书定义[φ,ψ](X,Y)=[φ∧ψ](X,Y)=[φ(X),ψ(Y)]-[φ(Y),ψ(X)],于是[ω∧ω](X,Y)=[ω,ω] (X,Y)=2[ω(X),ω(Y)],这样嘉当方程简写为Ω=dω+(1/2) [ω,ω]或Ω=dω+(1/2) [ω∧ω].
(2)将嘉当结构方程代入,得▽Ω(X,Y,Z)=▽dω(X,Y,Z)+(1/2)▽[ω,ω](X,Y,Z). 由于▽dω(X,Y,Z)=ddω(hX,hY,hZ)=0,且在水平向量上ω恒为零,[ω,ω]是一个垂直的2次形式,故▽[ω, ω]=d[ω,ω]·h=0.
为什么上述方程称为嘉当结构方程呢?下面就把它与前面在李群中讲的结构方程和活动标架法中讲的嘉当结构方程联系起来。设Γ是线丛L(M)上的联络,对应的联络形式为ω,它是取值于李代数gl(n,R)的1形式。根据李代数基的不同选择,有两种证明方法:
(1)设gl(n,R)的基为) ,其中
,其中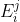 是n×n矩阵,它的第i行第j列的元素为1,其余为零。
是n×n矩阵,它的第i行第j列的元素为1,其余为零。
(2)基为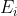 ,满足
,满足
后一种角标少,运算简洁,我们只介绍后一种。令 和
和 分别是P中关于基
分别是P中关于基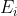 的一个联络的联络形式和曲率形式。于是
的一个联络的联络形式和曲率形式。于是
,\omega (Y)] %3D \omega (X)\omega (Y) - \omega (Y)\omega (X))
E_i \omega ^j (Y)E_j - \omega ^j (Y)E_j \omega ^i (X)E_i)
\omega ^j (Y)[E_i ,E_j ] = \omega ^i (X)\omega ^j (Y)c_{ij}^k E_k)
\omega ^j (Y) - \omega ^j (X)\omega ^i (Y))c_{ij}^k E_k)
)
所以,通过李代数的基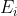 ,纤维丛的结构方程就成为
,纤维丛的结构方程就成为

对于j<k,上式简化为

将外微分d作用于该方程,对于2次形式Ω和一次形式ω,得
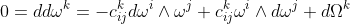
利用
 %3D \frac{1}{{2!1!}}\delta _{123}^{i_1 i_2 i_3 } [\Omega (X_{i_1 } ,X_{i_2 } ),\omega (X_{i_3 } )])
,\omega (Z)]\delta _{123}^{231} [\Omega (Y,Z),\omega (X)])
,\omega (Y)]\delta _{123}^{132} [\Omega (X,Z),\omega (Y)])
,\omega (Z)]\delta _{123}^{321} [\Omega (Z,Y),\omega (X)])
及
 %3D \frac{1}{{1!2!}}\delta _{123}^{i_1 i_2 i_3 } [\omega (X_{i_1 } ),\Omega (X_{i_2 } ,X_{i_3 } )])
注意到对于水平向量X,Y,Z有ω(X)=ω(Y)=ω(Z)=0
即可证明 %3D \omega ^i \wedge d\omega ^j (X,Y,Z) = 0)
于是 %3D 0) . 这就是比安基恒等式。
. 这就是比安基恒等式。
无处不在的嘉当结构方程。
4.规范场
酝酿已久的革命终于到来了。不过这篇文章中不准备广泛讨论各种规范场,只讲讲最简单的规范场——电磁场,因为我刚本科毕业,还没学量子场论,所以杨米尔斯场等问题以后再说。
假定有粒子场ψ(x),它是复数场。规范在很多时候是指模为1,即规范变换
 \to \psi '(x) %3D e^{i\omega (x)} \psi (x))
这相当于在闵可夫斯基空间 中的每一点x处,选取U(1)群中的一个元素
中的每一点x处,选取U(1)群中的一个元素}) ,并将它作用于ψ,这导致了底流形为
,并将它作用于ψ,这导致了底流形为 ,结构群为U(1)的纤维丛,其中
,结构群为U(1)的纤维丛,其中
} \psi (x) \to \psi (x)) 为丛投影,
为丛投影, \to e^{i\omega (x)} \psi (x))
为局部截面。对于联络一次形式ω,定义 ,其中U为M上一个局域,
,其中U为M上一个局域, 诱导出拉回映射
诱导出拉回映射) \to \Lambda (U)) ,使我们由楼上(丛空间)到楼下(底空间),
,使我们由楼上(丛空间)到楼下(底空间),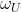 是M的局域U上的g值(g为李代数)一次形式,称为(局部)规范势。形象地说,我们利用拉回映射将联络形式ω从楼上拉到楼下成为
是M的局域U上的g值(g为李代数)一次形式,称为(局部)规范势。形象地说,我们利用拉回映射将联络形式ω从楼上拉到楼下成为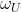 ,就是规范势。
,就是规范势。
对于闵可夫斯基流形上的U(1)主丛,纤维F=结构群G=U(1)={exp(iθ)},对U(1)丛有一个自然的右乘作用。对于主丛P上的联络ω,从李群G=U(1)= {exp(iθ)}的李代数g=u(1)={iθ}可知,对于局部截面 而言,
而言, 是U上
是U上
的{iθ}值1形式,可令) . 由于一次形式均可表示为
. 由于一次形式均可表示为
 故
故 .
.
设 为另一局部截面,
为另一局部截面,) 为U与V中的一点。前面说了,结构群就是转移函数构成的集合,故对于U(1)丛,转移函数为
为U与V中的一点。前面说了,结构群就是转移函数构成的集合,故对于U(1)丛,转移函数为 %3D e^{i\theta (x)} \in U(1)) . 对
. 对 两边微分,得
两边微分,得 . 令
. 令 %3D e^{i\theta (x)}) ,则
,则 %3D 0) . 这说明
. 这说明 是一个1次闭微分形式。由于
是一个1次闭微分形式。由于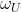 与
与 均为1次微分形式,它们可能只相差一个1次闭微分形式,所以可假定
均为1次微分形式,它们可能只相差一个1次闭微分形式,所以可假定
 . 代入
. 代入 %3D e^{i\theta (x)}) ,注意到
,注意到 可得
可得 ,这就是我们在经典电动力学中熟知的规范变换。所以说规范变换就是通过结构群(转移函数的集合)从一个联络形式(规范势)到另一个联络形式(规范势)。
,这就是我们在经典电动力学中熟知的规范变换。所以说规范变换就是通过结构群(转移函数的集合)从一个联络形式(规范势)到另一个联络形式(规范势)。
对于U(1)丛上的联络形式ω,可以定义物理上的场强F=i▽ω=iΩ. 由此,对于局部截面
 ,利用U(1)为阿贝尔群(可交换)得
,利用U(1)为阿贝尔群(可交换)得 .于是
.于是
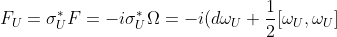 = - id\omega _U = - dA_U)
 = \frac{1}{2}(\partial _j A_{U_i } - \partial _i A_{U_j } )dx^i \wedge dx^j = \frac{1}{2}F_{ij} dx^i \wedge dx^j)
 正是电磁场张量。而
正是电磁场张量。而
 = d( - id\omega _U ) = - id\Omega _U = - i[\Omega _U ,\omega _U ] = 0)
就是齐次麦克斯韦方程。类似地,设 ,则
,则 就是非齐次麦克斯韦方程,其中δF表示F的余微分,是外微分d的对偶运算。
就是非齐次麦克斯韦方程,其中δF表示F的余微分,是外微分d的对偶运算。
由于量子力学与李群有关,广义相对论与黎曼几何有关,规范场与纤维丛有关,超弦与代数几何有关,所以物理学家要深入研究物理就必须对它们有所了解。在这篇文章中,我将对李群、黎曼几何与纤维丛做一个初步介绍(代数几何比较深奥,等我学完它的预备知识“交换代数与复分析”再说)。由于我是初学者,理解错误在所难免,所以外行请不要盲目相信,内行看出错误请指出来哪里错了,正确的理解是什么。就当我是抛砖引玉吧。
一、预备知识
1.切向量
设
为简化运算,上式使用了爱因斯坦求和约定,即重复出现的一对(上下)指标表示求和Σ.
但是,这样的定义依赖于欧式空间的线性结构。为了推广到一般的流形上去,我们必须给出另一种定义。我们假定读者已经熟悉流形的概念,不熟悉的可以看看我以前的拙作《现代微分几何的基本概念》。
设U为流形M上一个坐标邻域,p为U中一点。
设γ: (- ε, ε) →M是光滑流形M中过
即
这说明任意向量v均可表示为
流形上某一点的所有切向量的集合称为该点的切空间,流形上所有切向量的集合称为切向量场。
2.诱导映射
设
除了流形之间可以定义可微映射,流形的切空间之间也可以定义诱导映射。
设
类似于切映射,还可定义余切空间(切空间的对偶空间)之间的余切映射。
设
下面讲主丛上的联络时会用到余切映射这个结果,即
注意,虽然
3.微分形式
微分形式我们已经在《微分形式与同调论浅析》中介绍过了。这里只是补充一个重要公式
dω(X,Y)=Xω(Y)-Yω(X)- ω([X,Y]),这个公式在李群的嘉当结构方程及黎曼几何的嘉当结构方程的证明中都是关键的一步。
为证明这个公式,我们先证明另一个重要公式df(X)=X(f). 设流形上的向量场为
则
有了这个公式,就可以给出dω(X,Y)=Xω(Y)-Yω(X)- ω([X,Y])了。设有一次形式ω=fdg,其中f,g为函数(零次微分形式),则
dω(X,Y)=d(fdg)(X,Y)=(dfΛdg-fddg)(X,Y)=(dfΛdg)(X,Y)=df(X)dg(Y)-dg(X)df(Y)
=(Xf)(Yg)-(Xg)(Yf)=X(f(Yg))-Y(f(Xg))=X(f(Yg))-Y(f(Xg))-f(XYg-YXg)
=X(fdg(Y))-Y(fdg(X))-fdg(XY-YX)= Xω(Y)-Yω(X)-ω([X,Y])
4.向量场的积分曲线
既然每一根曲线在每一点都有一个切向量,那么是否任意给定一个向量场,就有可能从某一点P开始作出一条曲线,使该曲线上任意一点的切向量就是此向量场在这一点的向量?回答是,对于
该向量场的分量是
二、李群
1.李群
设G是一个非空集合,如果G是一个群,并且G还是一个光滑流形,则称G是一个李群。可见,李群集代数、几何性质于一身。
物理系的群论课程一般都会讲到李群的代数性质,但很少讲李群的几何方面,因为量子力学、量子场论的问题差不多都能在群论的框架下解决,而不必牵涉几何学;相对论对几何学依赖性比较大,但又不牵涉到群论。总之,群论的几何方面被一部分物理学家忽视了。然而,根据克莱因的观点,几何学与变换群密不可分。实际上,纤维丛就是这样一个既涉及流形、又涉及群的结构。本文最终是要定义主纤维丛上的联络,那么自然要在群论的几何方面多洒点笔墨。我们先简单回顾李群的代数性质,然后详细讲讲李群与微分几何的联系。
2.李代数
化难为易,把李群线性化,即寻找一个有限维的线性空间来近似代替它,通过对这个线性空间的深入研究来窥见李群的性质,便成为数学家的一个心愿。李代数就是这样一个线性空间。为了给出李代数的概念,先要定义李括号。
给定一个坐标系x^i ,那么用
所以,换位子(李括号)
是一个非零向量场,它的分量一般不是零。
容易验证,李括号满足线性[aX+bY,Z]=a[X,Z]+b[Y,Z],反对易性[X,Y]+[Y,X]=0和雅克比恒等式[X,[Y,Z]]+[Y,[Z,X]]+[Z,[X,Y]]=0,故向量场关于李括号构成了一个李代数。李代数构成了量子力学的基础,例如角动量问题可以归结为求解SO(3)或SU(2)的李代数方程。一般的群论书在这方面讲的很详细,而且也很好理解,所以我就不再赘述了。下面开始讨论李群的几何方面。
3.李导数
在正式引出李群对几何的作用之前,先看看李群是怎么进入几何学的。
向量场的积分曲线汇给出了此流形到其自身中的一个自然映射。如果λ是这些曲线的参数,则任意足够小的数Δλ定义了一个映射,它把每一点映成线汇中同一根曲线上参数再增加Δλ的那一点。这种映射称为沿该线汇的一个“拉曳”。
有了拉曳的概念就使我们能沿着线汇定义导数。定义向量场和张量场导数的任何努力都有一个内在的困难.考虑一下,如果把向量场的导数定义为:不同点的向量之间的差除以这两点之间的距离,再取极限,那问题之一是如何去定义点之间的“距离”.如果这两点都在一根曲线上的话,则我们可以把这段距离取为这两点的参数值之间的差.(这就给出关于参数的导数,而在没有度规的流形上,能做到的就是这一点了.)更严重的问题是对不同点的向量的比较:不同点的两个向量“平行”与否,在欧几里得平面中,这是一个容易回答的简单问题.在弯曲的曲面上这一问题可能没有唯一的答案.在一个简单的可微流形上,在不同点的平行问题甚至是没有意义的,因为此时不存在标志或标尺,用以平行地移动向量.为了定义绝对平行,此时必须在流形上附加其他的结构,即所谓仿射联络,我们下面讲黎曼几何时再来研究这个问题.在这里我们将考虑另一种方法,它在线汇起主要作用的那些问题中是可用的.线汇本身能代替不同点平行的概念.也即当要比较同一曲线上位于点λ和λ+Δλ处得向量时,我们就可以把在λ+Δλ处得向量拉曳到λ处,这就在λ处定义了一个新向量,从λ处得原向量减去这个新向量就定义了两者之差。首先考虑一个标量函数f,求它在λ+Δλ的值,拉回到λ点,减去该标量函数在λ点的值,除以Δλ,并取极限Δλ→0.通过拉回映射我们定义了一个新标架场f*,它的值由df*/dλ=0定义,所以它在λ处的值与λ+Δλ处得值是一样的,即f*(λ)=f(λ+Δλ).于是Lv(f)=lim[f*(λ)-f(λ)]/ Δλ=lim[f(λ+Δλ)-f(λ)]=df/dλ.我们把Lv(f)称为f的李导数。
任意向量场由曲线的线汇所定义。设有两个线汇μ和λ,在d/dλ映射下,μ线汇的任意曲线映为一根新曲线,它是原来曲线上各点在李拉曳下的象构成的新点的集合,所形成的曲线就定义了参数为
向量场是用其对函数的作用来定义的。所以场U=d/dμ在
由[U*,V]=0及
及
则
于是
由于μ*与μ只差Δλ的一次项,故可用d/dμ代替d/dμ*,于是
即两个向量场的李导数就是它们的李括号。而李括号构成李代数,所以李导数诱导了李代数。
4.李氏变换群
下面开始讨论李群对几何的作用。
设M是一个m维光滑流形,G是r维李群。若θ:M×G→M是光滑映射,记为θ(x,g)=x·g,使得对M中任意点x和G中任意元素g,h满足x·e=x,(x·g)·h=x·(g·h),则称G是右作用在M上的李氏变换群。类似地,若σ:G×M→M为σ(g,x)=g·x,满足e·x=x,g·(h·x)=(g·h)·x,则称G是左作用在M上的李氏变换群。
设G是右作用在M上的李氏变换群,若对G中任意一个非单位元素g,都有M中一点x,使得x·g≠x,则称G在M上的作用是有效的。特别地,若该变换为光滑同胚,则称G在M上的作用是自由的(或称G在M上的作用没有不动点)。
设G是左作用在M上的李氏变换群,若对于M中任意两点x,y,必有G中一个元素g使得y=g·x,则称G在M上的作用是可迁的。此时称M为齐性空间。令H={g ,满足 g·x=x},则H为G的闭子群,称为变换群G关于基点x的迷向群(亦称各向同性群)。
如果上述x不是M中的点,而是G中的元素,则把上述σ(g,x) 写成Lg(x),把θ(x,g)写成Rg(x),即Lg(x)=g·x , Rg(x)=x·g.由于Lg和Rg都是G到自身的光滑映射,由于
设X为光滑切向量场中的一个切向量,若对G中任意g都有
设U是光滑流形M的一个开子集,若在U上每一点p都指定切空间TpM的一个h维子空间
我曾在《微分形式与同调论浅析》中介绍过微分形式,并且上面还补充了一个公式dω(X,Y)=Xω(Y)-Yω(X)- ω([X,Y]). 现在,我们就用它研究李群和黎曼几何。这一节先讨论李群上的微分形式,黎曼几何的微分形式在下面讲到活动标架法时再介绍。设ω为李群流形G上的一次微分形式,若(Lg)* ω=ω,则称ω为李群G上的左不变一次微分形式。与
即ω(X)是G上的常值函数(下面讲纤维丛上联络的曲率时会用到这一结果)。
若ω为1次微分形式,则dω为2次微分形式。一般地,1次微分形式可写为ω=f(x)dx,2次微分形式可写为
设
设
由于
{\omega ^j (X_s )})
而
于是
这就是著名的嘉当结构方程。这是李群的嘉当结构方程,后面我们还会谈到黎曼几何的嘉当结构方程、纤维丛的嘉当结构方程。
5.单参数变换群
假定我们有一个解析流形,同时假定向量场V=d/dλ的积分曲线上点的坐标为
所以,通过指数运算exp(εV ),我们把
考察过e的左不变向量场V的积分曲线,它在e处有唯一的切向量Ve,并且有唯一的参数t,当t=0对应e. 曲线上的点可用V的指数映射exp(tV)来定位。这正好包含由向量场V生成的变换群G到自身的微分同胚。不像一般的向量场,V完全由Ve确定,因此我们把G在此曲线上的点用
这个群就称为G的单参数子群。这很简单,因为指数化乘为加,群乘法相当于参数值的加法。切空间中每一个向量都有唯一的一个子群;而且,因为每一个单参数子群都是G中通过e(子群总包括单位元素)的一根光滑曲线,所以在G的单参数子群与G的李代数元素之间有一个一一对应。
6.李群的伴随表示
李群和李代数的表示论已经成为一个非常深刻的专门理论,它在李群、李代数的结构理论,齐性空间、对称空间上的调和分析,泛函分析,微分几何以及物理学等各个方面有着广泛的应用,这里我们只介绍李群及其李代数的一种自然的、因而十分重要的表示,称为伴随表示,其表示空间是李群的李代数本身,它在我们下面定义纤维丛上的联络时起着关键的作用。
对于G中任意的g、h,定义映射ad(g):G→G如下:
我们已经定义了Lg*ω=ω,很自然的问题便是,Rg*ω=?这就是我们在引入主丛联络时要讲的。实际上,它就是ω的伴随表示
如果说满足Lg*ω=ω的ω为左不变微分形式,那么满足Rg*ω=ω的ω就可以叫做右不变微分形式。同时满足左不变和右不变的ω就可以称为双不变微分形式。呵呵,上帝是个左撇子,对左不变比较偏爱,所以历史上并不曾有人定义右不变向量场和右不变微分形式,虽然有人定义了双不变,但那是指李群的双不变黎曼度量,即
设F是李群(流形)M到李群(流形)N的同态(映射),满足
唉,一个通宵就写了这么点,太累了,剩下的下午再写吧。先把提纲列出来:
三、黎曼几何
弯曲空间中最重要的概念是曲率,要给出曲率必须先定义导数。但是,我们通常熟悉的长度、角度等与度规有关的几何概念,在流形中是没有的,它们不是流形的内禀性质,也不可能在流形的微分结构中自然产生。要定义导数,必须在流形上附加新的结构。前面定义的李导数是一种附加结构(线汇),这里我们给出另一种附加结构——联络。确切地说,就是通过曲面上的平行移动定义列维-奇维塔联络。弯曲空间的平行移动和列维-奇维塔联络在拙作《现代微分几何的基本概念》中已经介绍过了,这里不再重复。这里来讲讲比较现代的活动标架法和公理化方法。当然,为了照顾初学者,让我们从欧式空间的曲线坐标讲起。这是通常张量分析的内容,熟悉张量分析(主要是张量的协变导数)的读者可以跳过曲线坐标这一节,直接进入活动标架法。
1.曲线坐标
假定在欧式空间
因为在不同点的自然标架不是互相平行的,所以计算它从一点过渡到邻近点的变差就很重要,特别是自然标架场沿坐标曲线的微商。设v,w是定义在区域V上的两个向量场,用自然标架表示为
即
设l(t)为一条光滑曲线,t为该曲线的参数(当该参数t选为弧长s时,该曲线就称为测地线)。设l(t)上每点的切向量为
如果
将参数t改成弧长s,此时平行移动的方程称为测地线方程。上述方程可以写成
有点像薛定谔方程
有人说薛定谔方程是一种特殊的测地线方程,但各项的物理意义是什么我不清楚。尤其是,为什么哈密顿量为
我们讨论了半天
同理可得
假定二阶混合偏导与次序无关,即
由此可推导出
令
我们把
2.活动标架法
为了容易理解,在正式给出活动标架法之前,先看看大部分读者比较熟悉的仿射空间(定义了仿射坐标系,即斜角坐标系的欧式空间)上的微分形式。
设A³是一个3维仿射空间,它的一个标架是指A³中一点P及其与之相伴的向量空间(伴随向量空间)V的一个基底
在标架空间
横看成岭侧成峰。从标架空间
即
对上式求外微分,得
由于
这就是仿射空间的结构方程。
考虑曲线坐标
定义
故
意味着挠率和曲率为零,这是平直空间的基本特征。对于弯曲空间,曲率一般不为零;并且,有时候挠率也不为零。与前面对曲线坐标的讨论对比可知,二阶混合偏导为零时联络是对称的,挠率为零。
推而广之,可以定义挠率形式和曲率形式为:
利用前面证明的公式dω(X,Y)=Xω(Y)-Yω(X)- ω([X,Y])
及外积定义
设
由此可定义
则对于曲率形式有
并定义
3.公理化
前面已经提到,挠率和曲率可以不必依赖于空间的度量性质,而定义为
事实上,按量子力学的看法,所有算子都是一种变换,作用在一个函数上给出另一个函数。所以,曲率、挠率乃至协变导数等其实都可以定义为一种映射(集合之间的变换)。算子本身可以看做附加在流形上的一种结构,而不必要求这种结构是从黎曼度量张量诱导出来的。下面我们就来介绍公理化方法。
设M是一个光滑流形,若有一个映射▽,对于任意向量场X,Y,Z和函数f均有:
(1)
(2)
(3)
(4)
则称▽为光滑流形M上的一个联络。
之所以能公理化,是因为联络是不依赖于度量的;之所以要公理化,是为了运算简洁和符号美观。例如,设
则
这是黎曼几何最美的公式之一,要问如何三步写出测地线方程?呵呵,除此之外,别无捷径。
黎曼几何还有许多美丽的公式,比如:
挠率
曲率
黎曼几何基本定理
比安基恒等式R(X,Y)Z+R(Y,Z)X+R(Z,X)Y=0或R∧θ=0
▽R(X,Y,Z,W,T)+▽R(X,Y,W,T,Z)+▽R(X,Y,T,Z,W)=0或dR=ω∧R-R∧ω
4.爱因斯坦方程
下面我们简单介绍下爱因斯坦的引力场方程。我们已经定义了曲率张量,它是一个逆变指标(上标)和三个协变指标(下标)的四阶张量。利用协变黎曼度量张量(二阶),可以把上标降下来(逆变度量张量将下标升上去),得到四个协变指标的四阶张量。根据张量运算规律,如果有一对(一上一下)指标相同,则约定求和,为哑标。所以,逆变度量张量与曲率张量的协变指标有两对相同时,通过缩并(有的书称为求迹,即矩阵元之和)运算就可以将四阶曲率张量变成一个二阶的新张量,这个新张量称为里奇张量。用同样办法将里奇张量再缩并一次,就得到一个标量,称为曲率标量R. 用二阶逆变曲率张量R^(μυ)减去逆变度量张量g^(μυ)与曲率标量R之积的一半定义了一个二阶对称张量G^(μυ),称为爱因斯坦张量。则G^(μυ)=KT^(μυ)就是引力场方程,其中K=-8πG/(c)^4为常数,T^(μυ)为能量动量张量。
如果粒子受到力的作用,则粒子运动的轨道就不是R³中的短程线了。更精确地说,如果我们坚持从平直空间的几何来看问题。则受力作用的粒子在该空间中就不是直线了.但是,我们也可从另一个角度来看问题,即把力几何化,认为现在空间不再是平直空间.而粒子运动轨道是这一新的几何中的短程线.
略为认真考虑一下,我们就会发现,力的几何化使我们必须从3维几何转到4维的几何上去。这一点可以阐明如下:例如我们在地面上的同一地点、以同样的角度而两种不同的速率发射两颗子弹,它们在地球引力的作用下显然将沿不同的轨道运动.现在,我们试图把引力场几何化,而给予3维空间某种新的结构,这样做是否能使这两条轨道都是该3维几何学中的短程线呢?仔细分析一下。就可以知道这是不行的,这是因为上述两条不同的轨道。出发于同一点,且在该点有相同的切线,所以如果它们是该3维几何中的短程线,则它们将是重合的,这就矛盾了.因此这一问题的出路是把时间放到我们的几何中来。引力的几何化使这个4维空间有了一个弯曲的结构,即黎曼曲率张量不为零。而这两条轨道现在都是该4维儿何中的短程线。现在。这是可能的,因为这两颗子弹的初速度是不同的.在此4维空间中,在开始时刻也不再是相切的了。可以各自成为一条短程线.以上正是广义相对论的基本思想之一。
把这种思想梢加引伸,我们也可以再考虑电磁力的几何化问题,举个简单的例子就会使我们看出解决问题的出路了.我们把上面的例子再扩展一些,假定地球是带正电的,那么在地球上同一点以同样速度发射各带正电和负电的两颗子弹,我们在R3中会得到两条不同的轨道。为了要使它们都是短程线,则原有的4维几何又待“改进了”.此时,我们要再加“电磁”这一维,才能使电磁力也几何化,这正是卡鲁扎-克莱因在本世纪二十年代提出引力和电磁力统一的理论思想,目前已成为一个广为研究的理论.我们下面就讨论它们的数学基础-一一纤维丛理论.
四、纤维丛
1.纤维丛
我们已经在《现代微分几何的基本概念》中介绍过切丛,即流形M与它在每一点的切空间T所构成的乘积流形TM. 下面我们介绍其他类型的纤维丛。
切空间是向量构成的集合,它的对偶空间称为余切空间,是由微分形式构成的集合。类似于切丛,可以把流形M与它的余切空间T*黏在一起定义,所得到的积流形T*M就称为余切丛。由于向量和微分形式都是张量的一种特殊情况(向量是具有一个上标的逆变张量,微分形式是具有一个下标的协变张量,一般的张量同时具有上下标),所以自然有张量丛的概念,而切丛和余切丛都是它的特例。
一般地,我们把上述积流形(即纤维丛)称为丛空间E(或全空间),M称为底流形(或底空间),而把切空间称为纤维型(或纤维空间)F. 由丛空间到底空间有投影映射(也称拉回映射)π,称为丛投影;由底空间到丛空间有推进映射s,并把满足复合映射π·s=id(id为恒等映射)的s称为纤维丛的截面。一般的纤维丛还包含结构群G,它作用于丛空间,从纤维上一点移到另一点,移动方法就是李群的左右移动。当纤维空间F为向量空间时,E就称为向量丛;当纤维空间F与结构群G相等(同构)时,E就称为主丛(为避免混淆,主丛记作P);把流形M上x点的切空间的一组有序基称为M的一个标架,x点及其这些标架构成的集合称为M上的线性标架主丛,简称线丛,记作L(M),其结构群为一般线性群GL(n,R),即所有n×n矩阵构成的集合。每个主丛P都有一个与之相伴的纤维丛E=(P×F)/G,称为伴丛,例如流形上的切丛就是线丛的伴丛。
我们曾比较过柱面与莫比乌斯带,前者是圆周与R的直积,后者不是直积。我们称满足直积的丛为平凡丛,不满足就称为非平凡丛。一般的纤维丛大多是非平凡丛。就像流形M局部同胚于欧式空间一样,虽然一个纤维丛整体上是非平凡的,不存在整体截面,但局部上是直积空间,这就导致局部平凡化和局部截面的概念。不同的纤维之间是无关的,为了联系它们,就要定义转移函数(也称变换函数)。转移函数的集合称为转移函数族,它正是纤维丛E的结构群G,在构造纤维丛时起着关键的作用。
在这里要强调一点:Do mathematics by picture!这个思想是阿诺尔德《经典力学的数学方法》讲的。关于映射最好的理解方法就是作图,这些抽象的逻辑推理一旦用图形画出来就变得非常简单。比如前面讲切向量的公理化定义,还有诱导切映射和余切映射,用图形思考就比用逻辑推理简单得多。这里也一样。考虑一个向量丛E. 我们可以建立一个平面直角坐标系,x轴表示底空间M,y轴表示向量空间(纤维空间)F,那么xy平面就是丛空间E. 于是x轴上的一个区间U就表示M的一个局域,x轴上一点m表示M上一点,y轴上一点n表示F中一点,xy平面内一点(m,n)表示E中一点。那么,什么是局部平凡化呢?什么是转移函数呢?就是在x轴上取区间U1与U2,假定交集非空,q为交集中一点,投影π将xy平面内一点(m,n)映射为x轴上一点m,π的逆映射π^(-1)将q点沿x=q提升到平面内(q,n)点,将区间U映射为y=n直线上的一个线段L. 设ψ为U×F到L的映射,U×F就是局部平凡化,即全空间局部上是底空间局域与纤维空间的乘积;ψ^(-1)为从L到U×F的映射。于是,ψ1为U1×F到L1的映射,ψ2为U2×F到L2的映射,(ψ2)^(-1)与ψ1的复合映射g=(ψ2)^(-1)·ψ1(q)将U1与U2交集中x=q上(q,0)点与(q,n)点之间的线段(q点处一根纤维)映射为(q,n)点,然后又将(q,n)点映射为(q,0)点与(q,n)点之间的线段(q点处一根纤维),总体效果是从一根纤维映射到一根纤维,所以复合映射g12就是上面所说的转移函数。纤维空间是向量空间,纤维之间的变换就像向量之间的变换矩阵(如我们早就熟悉的,两个向量之间通过二阶张量相联系)。所有变换矩阵g12构成一个群,它就是向量丛的结构群。
2.纤维丛上的联络
我们只介绍主丛上的联络,这个对于理论物理最为重要。一般纤维丛的联络可类似定义,有兴趣读者可参考相关书籍。
黎曼联络可以公理化,主丛联络也可以:主丛P(M,G)上的一个联络是一个线性映射,即对P中任意点p,M中任意点x,π(p)=x,[π^(-1)]x=Fx满足dπ·Γp=idTx(M)和
设切空间Tp(Fx)=Vp是切于纤维Fx的向量空间,称为竖直子空间(或垂直子空间),则主丛P中的联络Γ是对P中每个p点指定一个切空间Tp的水平子空间Hp,使得切空间分解为Tp=Hp+Vp,切映射满足dRgHp=Hpg. 对于M中每个向量场X,在P中都存在唯一的向量场
任取P上的光滑向量场X,在P中每点p,X可分解为X=vX+hX,其中vX和hX分别称为X的竖直分量和水平分量。竖直分量恒为零的向量场称为水平向量场,水平分量恒为零的向量场称为竖直向量场。在P(M,G)上给定一个联络Γ,则在P上存在一个g值(g代表结构群G的李代数)一次形式ω,称为联络形式,满足
(1)ω(X)=vX,即若X属于水平子空间Hp,则ω(X)=0
(2)
我们不做证明,只说明一下。第一条中的ω(X)为常数,这在讲微分形式中证明过;第二条中前一个等式我们在余切映射中讲过,后一个等式在李群的伴随表示中讲过。对证明感兴趣的读者可参阅陈维桓《黎曼几何引论》(下)。
3.联络的曲率
设P(M,G)为主丛,Γ为其中一个联络。考虑P上的一个与Γ相伴的p次形式ω,它在有限维向量空间中取值,则我们可以定义一个p+1次形式Ω=▽ω,它是一个g值(g为李代数)2次形式,称为联络的曲率形式(也称为称为外协变微分或外协变导数),为
简写为Ω=▽ω=dω·h. 其中X为P上光滑向量场,d为外微分,h为主丛P的切空间Tp到它的水平子空间Hp的投影(所以,如果这些X中有一个是竖直的,则▽ω=0)。这个曲率2次形式满足
(1)嘉当结构方程Ω(X,Y)=dω(X,Y)+[ω(X),ω(Y)]
(2)比安基恒等式▽Ω(X,Y,Z)=0.
证明:(1)将向量场分解为水平分量和竖直分量,分类讨论:
①X,Y都是水平的,则ω(X)=ω(Y)=0,于是嘉当方程化为Ω=dω,这正是Ω的定义;
②X,Y都是竖直的,则Ω(X,Y)=0(前面说了,这些X中有一个是竖直的,则▽ω=0),故只需证明dω(X,Y)+[ω(X),ω(Y)]=0;另外,前面讲微分形式时说过,ω(X), ω(Y)为常数,由于X,Y为切向量,而切向量等同于方向导数,故X(ω(Y))=Y(ω(X))=0;前面讲微分形式时证明了一个重要公式,即dω(X,Y)=Xω(Y)-Yω(X)-ω([X,Y]),故dω(X,Y)+[ω(X),ω(Y)]= dω(X,Y)+ω([X,Y])=Xω(Y)-Yω(X)=0-0=0=Ω(X,Y),所以嘉当方程成立
③X为竖直的,Y为水平的,则与②类似仍有Ω(X,Y)=0(X中有一个是竖直的则▽ω=0),故只需证明dω(X,Y)+[ω(X),ω(Y)]=0,结合dω(X,Y)=Xω(Y)-Yω(X)-ω([X,Y]),即只需证明Xω(Y)-Yω(X)-ω([X,Y]) +[ω(X),ω(Y)]=0;且Y为水平的使得ω(Y)=0,X为竖直的使得ω(X)为常数,从而Yω(X)=0,故只需证明ω([X,Y])=0. 下面我们就来证明。设φ(t)是由X生成的单参数子群,由于Y是水平的,故右移动的推进映射
是水平的,于是有ω([X,Y])=0.
注:有的书定义[φ,ψ](X,Y)=[φ∧ψ](X,Y)=[φ(X),ψ(Y)]-[φ(Y),ψ(X)],于是[ω∧ω](X,Y)=[ω,ω] (X,Y)=2[ω(X),ω(Y)],这样嘉当方程简写为Ω=dω+(1/2) [ω,ω]或Ω=dω+(1/2) [ω∧ω].
(2)将嘉当结构方程代入,得▽Ω(X,Y,Z)=▽dω(X,Y,Z)+(1/2)▽[ω,ω](X,Y,Z). 由于▽dω(X,Y,Z)=ddω(hX,hY,hZ)=0,且在水平向量上ω恒为零,[ω,ω]是一个垂直的2次形式,故▽[ω, ω]=d[ω,ω]·h=0.
为什么上述方程称为嘉当结构方程呢?下面就把它与前面在李群中讲的结构方程和活动标架法中讲的嘉当结构方程联系起来。设Γ是线丛L(M)上的联络,对应的联络形式为ω,它是取值于李代数gl(n,R)的1形式。根据李代数基的不同选择,有两种证明方法:
(1)设gl(n,R)的基为
(2)基为
后一种角标少,运算简洁,我们只介绍后一种。令
所以,通过李代数的基
对于j<k,上式简化为
将外微分d作用于该方程,对于2次形式Ω和一次形式ω,得
利用
及
注意到对于水平向量X,Y,Z有ω(X)=ω(Y)=ω(Z)=0
即可证明
于是
无处不在的嘉当结构方程。
4.规范场
酝酿已久的革命终于到来了。不过这篇文章中不准备广泛讨论各种规范场,只讲讲最简单的规范场——电磁场,因为我刚本科毕业,还没学量子场论,所以杨米尔斯场等问题以后再说。
假定有粒子场ψ(x),它是复数场。规范在很多时候是指模为1,即规范变换
这相当于在闵可夫斯基空间
为局部截面。对于联络一次形式ω,定义
对于闵可夫斯基流形上的U(1)主丛,纤维F=结构群G=U(1)={exp(iθ)},对U(1)丛有一个自然的右乘作用。对于主丛P上的联络ω,从李群G=U(1)= {exp(iθ)}的李代数g=u(1)={iθ}可知,对于局部截面
的{iθ}值1形式,可令
设
对于U(1)丛上的联络形式ω,可以定义物理上的场强F=i▽ω=iΩ. 由此,对于局部截面
就是齐次麦克斯韦方程。类似地,设




































No comments:
Post a Comment