(C严格凸意味着边界不存在直线段,具体说来就是任意x,y属于C,那么对于t属于(0,1),tx+(1-t)y一定是C的内点)
P是到C的投影算子(也就是说任意一点x,P(x)是C中到x最近的点)
问题是,现在取定空间中一点y,那么是否存在一个常数0<a<1,使得任意点z,都有
||P(y)-P(z)||<=a||y-z||
一些可以帮助思考的事实:
1、投影算子P一定是非扩张的,也就是说任意y,z,都有||Ty-Tz||<=||y-z||
2、因为C是给定的,且是有界严格凸的,所以C的边界的曲率应该在一个闭区间的范围内。我感觉这个a的大小应该和曲率的范围有关。
以上问题,如果哪位大神能给予解答,不胜感激!
这个问题已经在别人帮助下解决,答案是肯定的。
方法是借助截面曲率。
射影几何- 维基百科,自由的百科全书
https://zh.wikipedia.org/zh-hk/射影几何
在數學裡,投影幾何(projective geometry)研究在投影變換下不變的幾何性質。 ... 個例子為投影代數幾何(研究投影簇)及投影微分幾何(研究投影變換的微分不變量)。几何学- 维基百科,自由的百科全书
https://zh.wikipedia.org/zh-hk/几何学
透视投影的理論讓人們知道,幾何學不只是物體的度量屬性而已,透视投影後來衍生 ... 物件本體性質的研究,使幾何的主題繼續擴充,最後產生了拓扑学及微分幾何。凸組合、凸包與凸集| 線代啟示錄
https://ccjou.wordpress.com/2013/05/09/凸組合、凸包與凸集/
2013年5月9日 - 線代膠囊──正交投影矩陣 ... 幾何座標空間 \mathbb{R}^n ... 下面是凸集的基本定理,它說明純量乘法、向量加法和交集運算保留凸性(convexity)。外平行凸体的Minkowski均质积分 - 学位论文下载,博士论文
cdmd.cnki.com.cn/Article/CDMD-10663-2007214687.htm
轉為繁體網頁
轉為繁體網頁
由 赵雪华 著作 - 2007
三角恒等式凸集凸体凸表面曲率表面积体积正交投影均质积分外平行凸体平行 ... 几个三角恒等式的,这些恒等式是在证明和推广微分几何中经典的Euler公式时得到的.從歐幾里得到微分幾何(第5 頁)
episte.math.ntu.edu.tw/articles/sm/sm_18_06_1/page5.html
2002年2月17日 - 在幾何學的發展之中,有許許多多幾何學,像歐幾里得幾何學、投影幾何學……及其他種種幾何學,自然就要有一個人把它綜合集結起來,那就是德國 ...【简单问题】设X是n维欧式空间,C是X中一个有界严格凸的闭 ...
tieba.baidu.com/p/1344971051
轉為繁體網頁
微分几何吧 关注:1,410贴子:5,093 ... 设X是n维欧式空间,C是X中一个有界严格凸的闭凸集(C严格凸意味着边界不存在直线段,具体说来就是任意x,y属于C,那么 ...轉為繁體網頁
吴大任_百度百科
baike.baidu.com/view/251047.htm
轉為繁體網頁
研究领域涉及积分几何、非欧几何、微分几何及其应用(齿轮理论)。... ... 与陈省身成为同窗学友。1932年秋,吴大任应姜立夫之约回母校任助教,除批改学生作业外,轉為繁體網頁
O1 数学 - 上海交通大学图书馆
oldweb.lib.sjtu.edu.cn/view.do?id=603
轉為繁體網頁
... 实分析、实变函数O174.11 描述理论O174.12 测度论O174.13 凸函数、凸集理论O174.14 ... 射影(投影)几何O185.2 画法几何O186 微分几何、积分几何O186.1 微分 ... O186.16 大范围微分几何O186.17 直接微分几何O186.5 积分几何O187 代数 ...轉為繁體網頁
[DOC]变分几何、度量正则性及在非光滑优化中的应用 - 云南大学 ...
www.sto.ynu.edu.cn/docs/.../20140811112514781441.do...
轉為繁體網頁
轉為繁體網頁
2014年8月11日 - 二、Hilbert空间上闭凸集的投影定理是泛函分析中重要的几何定理,它是凸分析和 ... 三、收敛光滑函数列之导数序列的收敛性是微分学的基本性质。
凸組合、凸包與凸集
本文的閱讀等級:初級
幾何座標空間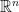 的一向量
的一向量 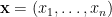 表示該向量端點的座標。點與座標向量具有一對一的對應關係,因為這個緣故,我們經常以座標向量代表點。本文介紹一種別於子空間與仿射空間 (子空間的平移) 的向量集。我們稱一向量集
表示該向量端點的座標。點與座標向量具有一對一的對應關係,因為這個緣故,我們經常以座標向量代表點。本文介紹一種別於子空間與仿射空間 (子空間的平移) 的向量集。我們稱一向量集  是凸集 (convex set),若給定任兩點
是凸集 (convex set),若給定任兩點  和
和  ,點
,點 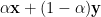 屬於
屬於  。淺白地說,在凸集中,任兩個點皆可「看見」彼此,連接這兩點的直線段不含集合以外的點。見下圖的例子。比較特別的是,
。淺白地說,在凸集中,任兩個點皆可「看見」彼此,連接這兩點的直線段不含集合以外的點。見下圖的例子。比較特別的是,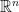 所包含的子空間與仿射空間都是凸集。
所包含的子空間與仿射空間都是凸集。
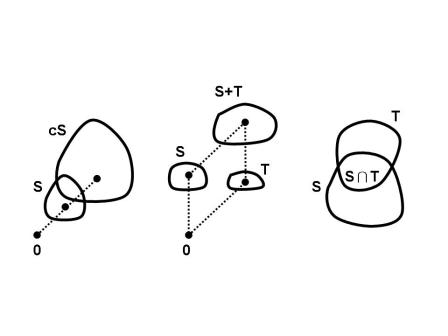
下面是凸集的基本定理,它說明純量乘法、向量加法和交集運算保留凸性 (convexity)。
定理一:對於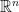 裏的凸集,下列性質成立:
裏的凸集,下列性質成立:
 且
且  ,可知
,可知  屬於
屬於  與
與  。因為
。因為  和
和  是凸集,
是凸集,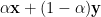 同時屬於
同時屬於  與
與  ,也就有
,也就有  ,證明
,證明  是一凸集。下圖顯示這三個凸集性質。
是一凸集。下圖顯示這三個凸集性質。
考慮幾何座標空間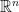 中
中 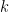 個點
個點 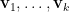 。我們定義
。我們定義 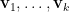 的凸組合 (convex combination) 為
的凸組合 (convex combination) 為
 ,
其中
,
其中  且每一
且每一 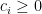 。凸組合是在線性組合的基礎下,加入係數和等於
。凸組合是在線性組合的基礎下,加入係數和等於 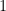 ,並限定係數不為負值。以
,並限定係數不為負值。以 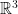 的兩個線性獨立向量
的兩個線性獨立向量 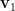 和
和  為例,所有的線性組合
為例,所有的線性組合  構成一穿越原點且包含
構成一穿越原點且包含 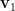 和
和  的平面。如果限制
的平面。如果限制 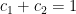 ,則稱為仿射組合;所有的仿射組合構成穿越
,則稱為仿射組合;所有的仿射組合構成穿越 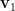 和
和  的直線 (見“仿射組合與仿射空間”)。再加入
的直線 (見“仿射組合與仿射空間”)。再加入  和
和  ,即為凸組合;所有的凸組合構成連接
,即為凸組合;所有的凸組合構成連接 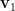 和
和  的直線段。對於一向量集
的直線段。對於一向量集  ,凸包 (convex hull) 是指
,凸包 (convex hull) 是指  所含向量的所有凸組合形成的集合,記作
所含向量的所有凸組合形成的集合,記作  。明顯地,單一點
。明顯地,單一點  的凸包為向量本身。下圖顯示
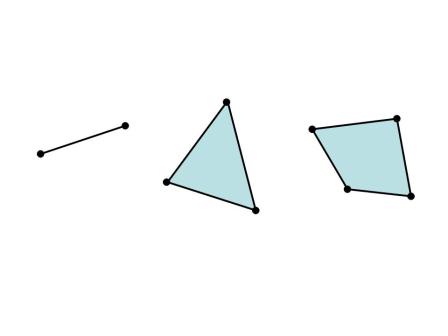
的凸包為向量本身。下圖顯示 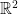 平面上二點、三點和四點產生的凸包。
平面上二點、三點和四點產生的凸包。
凸包 是一凸集嗎?是的。凸包
是一凸集嗎?是的。凸包  由向量集
由向量集  構成,可知
構成,可知 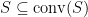 。定理二說明:若
。定理二說明:若  ,則
,則  是一凸集。因為
是一凸集。因為  的凸包為其自身,故可推論
的凸包為其自身,故可推論  是一凸集。
是一凸集。
定理二:若 中任何點的凸組合都屬於
中任何點的凸組合都屬於  ,即
,即  ,則
,則  是一凸集;相反陳述亦成立。
是一凸集;相反陳述亦成立。
我們用數學歸納法來證明。令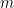 表示從
表示從  選取的點數。當
選取的點數。當 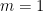 ,顯然該點是一凸集。當
,顯然該點是一凸集。當  ,兩點連成的直線段為一凸集。假設當
,兩點連成的直線段為一凸集。假設當 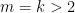 時,命題成立。考慮
時,命題成立。考慮 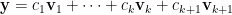 ,其中
,其中  且所有
且所有  。分開兩個情況討論。若
。分開兩個情況討論。若  ,則
,則  屬於
屬於  ,這時
,這時 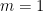 ,命題成立。若
,命題成立。若  ,令
,令  。因此
。因此  ,就有
,就有
 。
因為
。
因為  且每一
且每一  ,由歸納假設可知
,由歸納假設可知 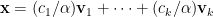 屬於
屬於  ,且
,且 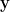 是
是  和
和  的凸組合,這時
的凸組合,這時  ,命題成立。
,命題成立。
給定一向量集 ,凸包
,凸包  有甚麼直觀意義呢?從幾何面來看,凸包
有甚麼直觀意義呢?從幾何面來看,凸包  是包含
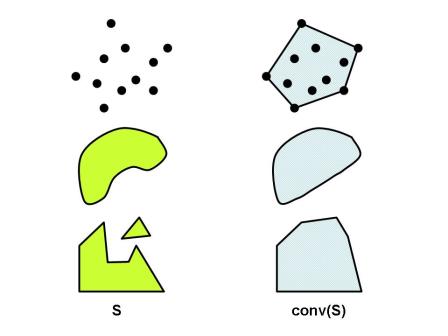
是包含  的「最小」凸集 (見定理三)。下圖描繪平面上的向量集
的「最小」凸集 (見定理三)。下圖描繪平面上的向量集  與對應的凸包
與對應的凸包  。
。
定理三:對於任意向量集 ,凸包
,凸包  等於包含
等於包含  的所有凸集的交集。
的所有凸集的交集。
令 表示包含
表示包含  的所有凸集的交集。定理一 (3) 指出
的所有凸集的交集。定理一 (3) 指出  是一凸集。因為
是一凸集。因為  是一凸集且
是一凸集且 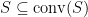 ,可知
,可知  。另一方面,
。另一方面, 包含
包含  推得
推得 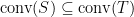 。因為
。因為  是一凸集,定理二說明
是一凸集,定理二說明  ,故
,故 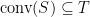 。合併以上結果即證明
。合併以上結果即證明  。
。
若 屬於凸包
屬於凸包  ,那麼
,那麼  可以寫成
可以寫成  中某些點的凸組合。但需要多少個點才足夠呢?定理四告訴我們:如果
中某些點的凸組合。但需要多少個點才足夠呢?定理四告訴我們:如果  ,最多只要
,最多只要 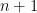 個點便可寫出凸包
個點便可寫出凸包  中任一點的凸組合表達式。以
中任一點的凸組合表達式。以 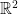 平面為例,對於任一
平面為例,對於任一  ,只要找到向量集
,只要找到向量集  中三個點使得
中三個點使得  位於此三點構成的三角形內即可;或找到二個點使得
位於此三點構成的三角形內即可;或找到二個點使得  位於這兩點連成的直線段上;甚至,如果
位於這兩點連成的直線段上;甚至,如果  ,則該點即為自身的凸組合。
,則該點即為自身的凸組合。
定理四:若 是一非空向量集,則任一屬於
是一非空向量集,則任一屬於  的向量必可表示成
的向量必可表示成  中
中 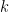 個點的凸組合,
個點的凸組合,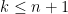 。
。
給定 ,我們要證明下列表達式存在[1]:
,我們要證明下列表達式存在[1]: ,其中
,其中 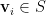 ,
, ,
,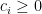 ,
,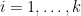 ,且
,且 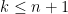 。若
。若  ,則
,則  必是仿射相依 (見“仿射獨立”,定理三),也就是說,存在不全為零的數組
必是仿射相依 (見“仿射獨立”,定理三),也就是說,存在不全為零的數組  使得
使得
 且
且  。考慮
。考慮
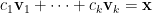 。
因為第一式乘以
。
因為第一式乘以 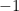 不造成影響且
不造成影響且  不全為零,故存在
不全為零,故存在 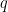 使得
使得 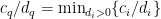 。置換指標
。置換指標 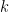 和
和 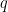 ,如此可使
,如此可使  且當
且當  時,
時, 。將第二式減去第一式通乘
。將第二式減去第一式通乘  的結果,消去
的結果,消去 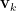 項,如下:
項,如下:
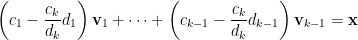 令
令 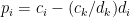 ,
, ,且
,且  。使用
。使用 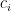 和
和  的性質,
的性質,
 ,
而且每一
,
而且每一 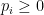 。理由如下:若
。理由如下:若 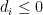 ,則
,則 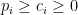 。若
。若  ,則
,則 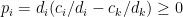 。所以,
。所以,
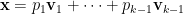 是
是 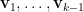 的一個凸組合。重複此程序至到
的一個凸組合。重複此程序至到 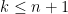 停止,因為這時仿射相依未必成立。
停止,因為這時仿射相依未必成立。
參考來源:
[1] 證明修改自 David C. Lay, Linear Algebra and its Applications, 4th ed., 2012, pp 457-458.
幾何座標空間
下面是凸集的基本定理,它說明純量乘法、向量加法和交集運算保留凸性 (convexity)。
定理一:對於
- 若
是一凸集且
是一實數,則
是一凸集。
- 若
和
是凸集,則
是一凸集。
- 若
和
是凸集,則
是一凸集。
考慮幾何座標空間
凸包
定理二:若
我們用數學歸納法來證明。令
給定一向量集
定理三:對於任意向量集
令
若
定理四:若
給定
參考來源:
[1] 證明修改自 David C. Lay, Linear Algebra and its Applications, 4th ed., 2012, pp 457-458.

No comments:
Post a Comment