Matrix67: The Aha Moments
经典证明:向量叉积的几何意义
为什么以向量 (a, b) 和 (c, d) 为邻边,构成的平行四边形的面积正好是 ad – bc 呢?下图是一个非常漂亮的无字证明。
 这是我在阅读 The Mathematical Mechanic: Using Physical Reasoning to Solve Problems 一书时受到启发并制作完成的。
这是我在阅读 The Mathematical Mechanic: Using Physical Reasoning to Solve Problems 一书时受到启发并制作完成的。
http://blog.sina.com.cn/s/blog_9283b6f601017hfw.html

http://blog.sina.com.cn/s/blog_9283b6f601017hfw.html
所谓点乘(也常称作内积),数学定义如下:
根据公式,我们可以得出 a·b=|a| |b|cosθ
定义向量 c = a - b 这样就形成了一个封闭的三角形,c向量为他的第三边
由于余弦定理我们可以知道c² = a² + b² - 2abcos(θ) (这里的a,b,c全部都是每一边的具体长度)
根据定义我们可以推导出c·c=c²(有兴趣的朋友可以去试着推导一下)
所以: c·c = a·a + b·b - 2abcos(θ)因为向量的点乘满足分配率:a·(b+c)=a·b+a·c
c = a - b
c·c = (a -b)·(a - b)
c·c = (a·a - 2a·b + b·b)
(a·a - 2a·b + b·b) = a² + b² - 2abcos(q)
约掉 a·a=a²,b·b=b²;
-2a·b = -2abcos(θ)
a·b = abcos(θ)
因为 a=|a|
所以 a·b=|a| |b|cosθ
跟据这个公式,我们能拿到两个向量之间的夹角,这对于判断两个向量是否同一方向,是否正交(也就是垂直),很有用处。具体判断如下:
a·b>0
a·b=0
a·b<0
所以,点乘的几何意义和用处就是计算两个向量之间的夹角,以及在某一方向上的投影。至于为什么要判断两个向量是否方向一致,这在3D中很有用处。比如:3D技术中的光栅化(光栅化的任务是为了绘制每个三角形单元,如何计算构成三角形单元的每个像素的颜色值)过程中,我们可以根据两个面的法向量的点乘判断两个面是否处于同一面,如果不是,那么只要光栅化其中需要显示出来的一面,而另一面我们就不用光栅化它(因为我们根本看不到被遮住的面),这样就节省了很多很多计算,能加快效率。
向量的叉乘(也叫做叉积)
为什么是这样,上面已经说过,规定就这样。
同样,我们给出叉乘的几何解释:
在3维几何中,我们可以一眼看出来,叉乘的结果也是一个向量,而且这个向量不是一般的向量,而是大名鼎鼎的"法向量",3D技术中法向量有多重要我就不吹了,反正是个VIP概念。
在2维集合中,axb等于由向量组成的平行四边形的面积(证明很简单,你们可以自己试着证明)
总之:向量的叉积最重要的应用就是创建垂直于平面,三角形,或者多边形的向量。
三维向量叉乘推导
一直以来,我都记不住向量叉乘的结果,每次都要查询。其根本原因在于,我没有去研究过叉乘是如何推导出来的。于是,这次想彻底解决一下。首先要感谢维基百科,它已经把所有问题都描述清楚了。
http://en.wikipedia.org/wiki/Cross_product
而下面的文字,只是我的读书笔记,以加深自己的印象。
首先我们知道 ,对于向量u和v, u x v的结果,是得到一个既垂直于u又垂直于v的向量,假设记作n.
则有下面公式
n = u x v;
而n的方向,是由右手法则决定的。 即伸出右手,四个手指方向从u绕到v. 此时,大姆指的方向,就是n的方向。 我们通常叫做右向量。
引用一下维基百科的图来说明问题,有兴趣的兄弟可以照图比划一下。 (注:图中向量是用的a x b来表示)
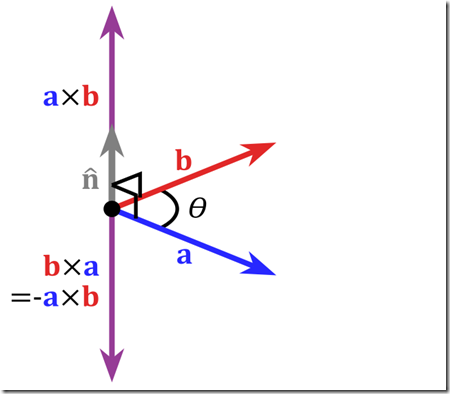
有了上面的知识,我们继续向下看。
我们假设向量 u,v,n分别用三个标量来表示。即
u = (Xu,Yu,Zu)
v = (Xv,Yv,Zv)
n = (Xn,Yn,Zn)
则,它们的关系为
Xn = Yu*Zv – Zu*Yv;
Yn = Zu*Xv – Xu*Zv;
Zn = Xu*Yv – Yu*Xv;
即 n = (Yu*Zv – Zu*Yv,Zu*Xv – Xu*Zv,Xu*Yv – Yu*Xv);
而为了验证n与u和v的垂直性,可以使用点乘进行
点乘法则比这个简单多了, u*v = (Xu*Xv + Yu*Yv + Zu*Zv) = dotUV;
如果两个向量垂直,则dotUV = 0;
代入验证一把
u*n = (Xu*(Yu*Zv – Zu*Yv) + Yu*(Zu*Xv – Xu*Zv) + Zu*(Xu*Yv – Yu*Xv));
= Xu*Yu*Zv – Xu*Zu*Yv + Yu*Zu*Xv – Yu*Xu*Zv + Zu*Xu*Yv – Zu*Yu*Xv;
把正负号的因式仔细比对一下,发现刚好可以低消。 结果为0.
v*n 同理可证。
于是,也验证了n与u,v垂直的特性。
如果只是为了应用的话,走到这一步就可以停下了。后面的知识,只是为了满足一下好奇心。
那我们就来看看,这个结论是怎么来的呢? 我们接着来推导。
为了更好地推导,我们需要加入三个轴对齐的单位向量。
i,j,k.
i,j,k满足以下特点
i = j x k; j = k x i; k = i x j;
k x j = –i; i x k = –j; j x i = –k;
i x i = j x j = k x k = 0; (0是指0向量)
由此可知,i,j,k是三个相互垂直的向量。它们刚好可以构成一个坐标系。
这三个向量的特例就是 i = (1,0,0) j = (0,1,0) k = (0,0,1)。
好,那对于处于i,j,k构成的坐标系中的向量u,v我们可以如下表示
u = Xu*i + Yu*j + Zu*k;
v = Xv*i + Yv*j + Zv*k;
那么 u x v = (Xu*i + Yu*j + Zu*k) x (Xv*i + Yv*j + Zv*k)
= Xu*Xv*(ixi) + Xu*Yv*(i x j) + Xu*Zv*(i x k) + Yu*Xv*(j x i) + Yu*Yv*(j x j) + Yu*Zv*(j x k) + Zu*Xv*( k x i ) + Zu*Yv(k x j) + Zu*Zv(k x k)
由于上面的i,j,k三个向量的特点,所以,最后的结果可以简化为
u x v = (Yu*Zv – Zu*Yv)*i + (Zu*Xv – Xu*Zv)j + (Xu*Yv – Yu*Xv)k;
于是,在i,j,k构成的坐标系中。集就是上面的结果。
当i = (1,0,0) j = (0,1,0) k = (0,0,1)时,我们通常省略i,j,k的写法。最终也就得到了我们的右向量。
叉乘的意义
叉乘表示垂直于uxv的右向量。
使用的地方
可以通过叉乘,修正向量关系,从而构建坐标系。 常见的有 摄相机矩阵和TBN空间转换矩阵的构建。
叉乘的矩阵表示法。
很多书上,包括 3D游戏大师编程技巧 上面,都是用的矩阵表示法来说明叉乘。
如下。
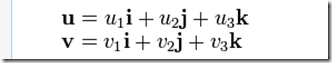
它对应的矩阵表示法为
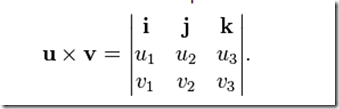
求其代数余子式,可以表示为如下
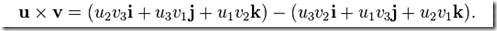
有了这个,那我们合并公因式i,j,k,则可以得到矩阵表示法
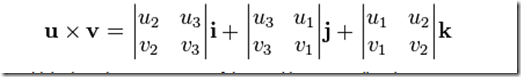
到此,叉乘的内容基本OK了。 值得说明的是,如果对方程组表示成矩阵不熟悉,就会感到不习惯,但是如果多多练习,我想应该是会习惯成自然吧。。。
根据公式,我们可以得出 a·b=|a| |b|cosθ
定义向量 c = a - b 这样就形成了一个封闭的三角形,c向量为他的第三边
由于余弦定理我们可以知道c² = a² + b² - 2abcos(θ) (这里的a,b,c全部都是每一边的具体长度)
根据定义我们可以推导出c·c=c²(有兴趣的朋友可以去试着推导一下)
所以: c·c = a·a + b·b - 2abcos(θ)因为向量的点乘满足分配率:a·(b+c)=a·b+a·c
c = a - b
c·c = (a -b)·(a - b)
c·c = (a·a - 2a·b + b·b)
(a·a - 2a·b + b·b) = a² + b² - 2abcos(q)
约掉 a·a=a²,b·b=b²;
-2a·b = -2abcos(θ)
a·b = abcos(θ)
因为 a=|a|
所以 a·b=|a| |b|cosθ
跟据这个公式,我们能拿到两个向量之间的夹角,这对于判断两个向量是否同一方向,是否正交(也就是垂直),很有用处。具体判断如下:
a·b>0
a·b=0
a·b<0
所以,点乘的几何意义和用处就是计算两个向量之间的夹角,以及在某一方向上的投影。至于为什么要判断两个向量是否方向一致,这在3D中很有用处。比如:3D技术中的光栅化(光栅化的任务是为了绘制每个三角形单元,如何计算构成三角形单元的每个像素的颜色值)过程中,我们可以根据两个面的法向量的点乘判断两个面是否处于同一面,如果不是,那么只要光栅化其中需要显示出来的一面,而另一面我们就不用光栅化它(因为我们根本看不到被遮住的面),这样就节省了很多很多计算,能加快效率。
向量的叉乘(也叫做叉积)
为什么是这样,上面已经说过,规定就这样。
同样,我们给出叉乘的几何解释:
在3维几何中,我们可以一眼看出来,叉乘的结果也是一个向量,而且这个向量不是一般的向量,而是大名鼎鼎的"法向量",3D技术中法向量有多重要我就不吹了,反正是个VIP概念。
在2维集合中,axb等于由向量组成的平行四边形的面积(证明很简单,你们可以自己试着证明)
总之:向量的叉积最重要的应用就是创建垂直于平面,三角形,或者多边形的向量。
三维向量叉乘推导
一直以来,我都记不住向量叉乘的结果,每次都要查询。其根本原因在于,我没有去研究过叉乘是如何推导出来的。于是,这次想彻底解决一下。首先要感谢维基百科,它已经把所有问题都描述清楚了。
http://en.wikipedia.org/wiki/Cross_product
而下面的文字,只是我的读书笔记,以加深自己的印象。
首先我们知道 ,对于向量u和v, u x v的结果,是得到一个既垂直于u又垂直于v的向量,假设记作n.
则有下面公式
n = u x v;
而n的方向,是由右手法则决定的。 即伸出右手,四个手指方向从u绕到v. 此时,大姆指的方向,就是n的方向。 我们通常叫做右向量。
引用一下维基百科的图来说明问题,有兴趣的兄弟可以照图比划一下。 (注:图中向量是用的a x b来表示)

有了上面的知识,我们继续向下看。
我们假设向量 u,v,n分别用三个标量来表示。即
u = (Xu,Yu,Zu)
v = (Xv,Yv,Zv)
n = (Xn,Yn,Zn)
则,它们的关系为
Xn = Yu*Zv – Zu*Yv;
Yn = Zu*Xv – Xu*Zv;
Zn = Xu*Yv – Yu*Xv;
即 n = (Yu*Zv – Zu*Yv,Zu*Xv – Xu*Zv,Xu*Yv – Yu*Xv);
而为了验证n与u和v的垂直性,可以使用点乘进行
点乘法则比这个简单多了, u*v = (Xu*Xv + Yu*Yv + Zu*Zv) = dotUV;
如果两个向量垂直,则dotUV = 0;
代入验证一把
u*n = (Xu*(Yu*Zv – Zu*Yv) + Yu*(Zu*Xv – Xu*Zv) + Zu*(Xu*Yv – Yu*Xv));
= Xu*Yu*Zv – Xu*Zu*Yv + Yu*Zu*Xv – Yu*Xu*Zv + Zu*Xu*Yv – Zu*Yu*Xv;
把正负号的因式仔细比对一下,发现刚好可以低消。 结果为0.
v*n 同理可证。
于是,也验证了n与u,v垂直的特性。
如果只是为了应用的话,走到这一步就可以停下了。后面的知识,只是为了满足一下好奇心。
那我们就来看看,这个结论是怎么来的呢? 我们接着来推导。
为了更好地推导,我们需要加入三个轴对齐的单位向量。
i,j,k.
i,j,k满足以下特点
i = j x k; j = k x i; k = i x j;
k x j = –i; i x k = –j; j x i = –k;
i x i = j x j = k x k = 0; (0是指0向量)
由此可知,i,j,k是三个相互垂直的向量。它们刚好可以构成一个坐标系。
这三个向量的特例就是 i = (1,0,0) j = (0,1,0) k = (0,0,1)。
好,那对于处于i,j,k构成的坐标系中的向量u,v我们可以如下表示
u = Xu*i + Yu*j + Zu*k;
v = Xv*i + Yv*j + Zv*k;
那么 u x v = (Xu*i + Yu*j + Zu*k) x (Xv*i + Yv*j + Zv*k)
= Xu*Xv*(ixi) + Xu*Yv*(i x j) + Xu*Zv*(i x k) + Yu*Xv*(j x i) + Yu*Yv*(j x j) + Yu*Zv*(j x k) + Zu*Xv*( k x i ) + Zu*Yv(k x j) + Zu*Zv(k x k)
由于上面的i,j,k三个向量的特点,所以,最后的结果可以简化为
u x v = (Yu*Zv – Zu*Yv)*i + (Zu*Xv – Xu*Zv)j + (Xu*Yv – Yu*Xv)k;
于是,在i,j,k构成的坐标系中。集就是上面的结果。
当i = (1,0,0) j = (0,1,0) k = (0,0,1)时,我们通常省略i,j,k的写法。最终也就得到了我们的右向量。
叉乘的意义
叉乘表示垂直于uxv的右向量。
使用的地方
可以通过叉乘,修正向量关系,从而构建坐标系。 常见的有 摄相机矩阵和TBN空间转换矩阵的构建。
叉乘的矩阵表示法。
很多书上,包括 3D游戏大师编程技巧 上面,都是用的矩阵表示法来说明叉乘。
如下。
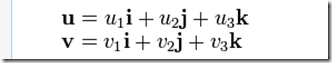
它对应的矩阵表示法为
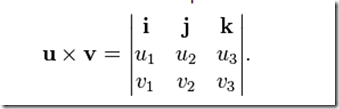
求其代数余子式,可以表示为如下
有了这个,那我们合并公因式i,j,k,则可以得到矩阵表示法
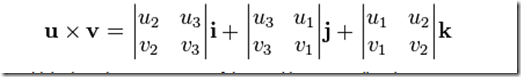
到此,叉乘的内容基本OK了。 值得说明的是,如果对方程组表示成矩阵不熟悉,就会感到不习惯,但是如果多多练习,我想应该是会习惯成自然吧。。。
posted on 2013-05-09 00:50 麒麟子 阅读(2660) 评论(0) 编辑 收藏 引用
[更新]将向量乘法“退化”到复数
作者:苏剑林 | 发布时间:February 4, 2011
向量有两个乘法:点乘和叉乘,其结果又分别叫做数量积和向量积。在很多情况下,用这两个定义的乘法运算都能够给我们带来很大的方便(其实它就是在实际问题中抽象出来的)。不过,也有相当一部分的二维问题用复数来描述更为简洁。于是,为了整合两者的巧妙之处,有必要把向量的两个乘法运算“退化”到复数中去(为什么用“退化”?因为向量是多维的,可以是3维、4维等,而复数运算只是二维的,很明显这是一种“退化”而不是“拓展”^_^)
运算法则:
点乘:
总法则:Z1∗Z2=|Z1||Z2|cos(argZ2Z1)
1∗i=0
i∗i=1
exp(iθ)∗exp(iφ)=cos(φ−θ)
iexp(iθ)∗exp(iφ)=−sin(θ−φ)
Z1∗Z2=Z1Z¯2+Z2Z¯1
叉乘:
由于二维向量的叉积都指向第三维,所以可以认为复数的叉积结果都是一个数。
总法则:Z1×Z2=|Z1||Z2|sin(argZ2Z1)
1×i=1
i×i=0
exp(iθ)×exp(iφ)=sin(φ−θ)
iexp(iθ)×exp(iφ)=−cos(θ−φ)
Z1×Z2=(Z1Z¯2−Z2Z¯1)i
变换关系:
Z1×Z2=−Z2×Z1
Z1×(iZ2)=Z1∗Z2
Z1∗(iZ2)=−Z1×Z2
微分恒等关系:
Z∗dZ=|Z|d|Z|
Z∗(idZ)=−(iZ)∗dZ=+−|Z|dZ∗dZ−(d|Z|)2−−−−−−−−−−−−−−√
(正负待定)
于是,复数便有了三种乘法了。它们代表的意义都不一样!复数原来的乘法是一种旋转和伸长,而点积和叉积分别是有关两个复数的夹角的余弦和正弦。
这是用复数研究三体问题周期轨道时所悟到的思想,特此记录!
读书频道 > 设计开发 > 其它开发 > 4.5.7 叉积
运算法则:
点乘:
总法则:
叉乘:
由于二维向量的叉积都指向第三维,所以可以认为复数的叉积结果都是一个数。
总法则:
变换关系:
微分恒等关系:
于是,复数便有了三种乘法了。它们代表的意义都不一样!复数原来的乘法是一种旋转和伸长,而点积和叉积分别是有关两个复数的夹角的余弦和正弦。
这是用复数研究三体问题周期轨道时所悟到的思想,特此记录!
读书频道 > 设计开发 > 其它开发 > 4.5.7 叉积
4.5.7 叉积
《3D游戏编程大师技巧(上、下册)》第4章三角学、向量、矩阵和四元,本章介绍了很多数学知识:向量、矩阵、参数化方程、复数、四元数等;这只是当今编写视频游戏所需数学知识的冰山一角。本节为大家介绍叉积。
AD:
4.5.7 叉积
另一种向量乘法是叉积。然而,仅当向量包含3个或更多分量时,叉积才有意义。因此,这里将以3D向量为例进行讨论。给定u = <ux,uy,uz>和v = <vx,vy,vz>,叉积u v的定义如下:
u v = |u|*|v|*sin( ) * n
下面逐项分析这个公式。|u|为向量u的长度,|v|为向量v的长度,sin( )是两个向量之间夹角的正弦。因此,|u|*|v|*sin( )是一个标量,即是一个数值。然后,我们将它与n相乘,但n是什么呢?n是一个单位法线向量,即它与向量u和v都垂直,且长度为1.0。图4.23图示了这种乘法。
因此,根据叉积可以知道向量u和v之间的夹角以及u和v的法线向量。然而,如果没有另一个公式,将无法得到任何信息。问题是,如何计算u和v的法线向量呢?答案是使用叉积的另一种定义。
叉积还定义为一种非常特殊的向量积。然而,如果不使用矩阵,将难以描述这种定义。要计算u和v的叉积(u v),可以建立一个这样的矩阵:
其中i、j、k分别是与x轴、y轴、z轴平行的单位向量。
要计算u和v的叉积,执行下面的乘法:
n = (uy*vz-vy*uz)*i - (ux*vz-vx*uz)*j + (ux*vy-vx*uy)*k
n是三个标量分别乘以三个相互垂直(即分别与x轴、y轴和z轴平行)的单位向量的线性组合。因此,可以省略i、j、k,将上述公式表示为:
n = <uy*uz-vy*uz, -ux*vz+vx*uz, ux*vy-vx*uy>
n是向量u和v的法线向量,但不一定是单位向量(如果u和v都是单位向量,n也将是单位向量),因此必须归一化以得到n。完成这一步后,就可以其代入到前面的叉积方程中,执行所需的计算。
然而,在实际应用中,很少有人使用公式u v=|u|*|v|*sin( )*n,而只是使用矩阵形式来计算法线向量,因为 通常是未知的。这里再次表明了对向量进行归一化在3D图形学中的重要性,您将使用归一化向量来进行光照计算、定义平面、比较多边形朝向、进行碰撞检测等。
叉积的乘法定律
下面列出叉积满足的乘法定律。
给定向量u、v和w以及标量k:
(a)u v =-(v u)(非常重要)
(b)u (v + w)=(u v)+(u w)
(c)(u+v) w=(u w)+(v w)
(d)k*(u v)=(k*u) v=u (k*v)
另一种向量乘法是叉积。然而,仅当向量包含3个或更多分量时,叉积才有意义。因此,这里将以3D向量为例进行讨论。给定u = <ux,uy,uz>和v = <vx,vy,vz>,叉积u v的定义如下:
u v = |u|*|v|*sin( ) * n
下面逐项分析这个公式。|u|为向量u的长度,|v|为向量v的长度,sin( )是两个向量之间夹角的正弦。因此,|u|*|v|*sin( )是一个标量,即是一个数值。然后,我们将它与n相乘,但n是什么呢?n是一个单位法线向量,即它与向量u和v都垂直,且长度为1.0。图4.23图示了这种乘法。
因此,根据叉积可以知道向量u和v之间的夹角以及u和v的法线向量。然而,如果没有另一个公式,将无法得到任何信息。问题是,如何计算u和v的法线向量呢?答案是使用叉积的另一种定义。
叉积还定义为一种非常特殊的向量积。然而,如果不使用矩阵,将难以描述这种定义。要计算u和v的叉积(u v),可以建立一个这样的矩阵:
 |
 |
| 图4.23 叉积 |
要计算u和v的叉积,执行下面的乘法:
n = (uy*vz-vy*uz)*i - (ux*vz-vx*uz)*j + (ux*vy-vx*uy)*k
n是三个标量分别乘以三个相互垂直(即分别与x轴、y轴和z轴平行)的单位向量的线性组合。因此,可以省略i、j、k,将上述公式表示为:
n = <uy*uz-vy*uz, -ux*vz+vx*uz, ux*vy-vx*uy>
n是向量u和v的法线向量,但不一定是单位向量(如果u和v都是单位向量,n也将是单位向量),因此必须归一化以得到n。完成这一步后,就可以其代入到前面的叉积方程中,执行所需的计算。
然而,在实际应用中,很少有人使用公式u v=|u|*|v|*sin( )*n,而只是使用矩阵形式来计算法线向量,因为 通常是未知的。这里再次表明了对向量进行归一化在3D图形学中的重要性,您将使用归一化向量来进行光照计算、定义平面、比较多边形朝向、进行碰撞检测等。
叉积的乘法定律
下面列出叉积满足的乘法定律。
给定向量u、v和w以及标量k:
(a)u v =-(v u)(非常重要)
(b)u (v + w)=(u v)+(u w)
(c)(u+v) w=(u w)+(v w)
(d)k*(u v)=(k*u) v=u (k*v)
【责任编辑:book
TEL:(010)68476606】
| 回书目 上一节 下一节 |

No comments:
Post a Comment