Thermal energy qm01 原子的化学性质，取决于它的核电荷数，而不是传统认为的原子量。The quantum of energy for a photon is not Planck's constant h itself, but the product of h and the frequency. The quantization implies that a photon of blue light of given frequency or wavelength will always have the same size quantum of energy. For example, a photon of blue light of wavelength 450 nm will always have 2.76 eV of energy. It occurs in quantized chunks of 2.76 eV, and you can't have half a photon of blue light - it always occurs in precisely the same sized energy chunks.

上帝掷骰子吗--量子物理史话 - 360Doc个人图书馆 www.360doc.com/content/08/.../80736_1981409.sht... Cached Translate this page Nov 22, 2008 - 在那个时代，他在力学和光学方面是仅次于牛顿的伟大科学家，可是似乎他 ..... 罗杰·彭罗斯（Roger Penrose）在他的名著《皇帝新脑》（The Emperor's ..... 普朗克再一次地注视他的公式，它究竟代表了一个什么样的物理意义呢？ ...... 人们现在已经知道，原子的化学性质，取决于它的核电荷数，而不是传统认为的原子量。   Early Photoelectric Effect Data Electrons ejected from a sodium metal surface were measured as an electric current. Finding the opposing voltage it took to stop all the electrons gave a measure of the maximum kinetic energy of the electrons in electron volts.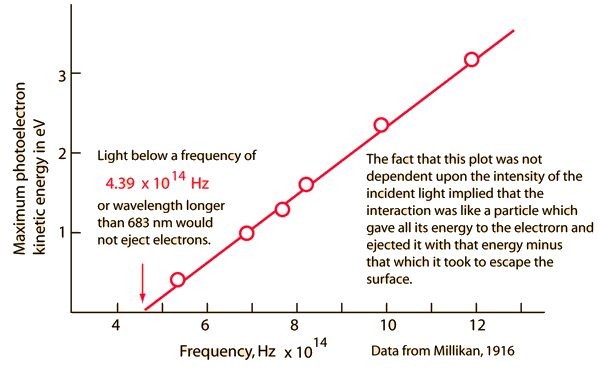 The minimum energy required to eject an electron from the surface is called the photoelectric work function. The threshold for this element corresponds to a wavelength of 683 nm. Using this wavelength in the Planck relationship gives a photon energy of 1.82 eV. Further analysis Table of photoelectric effect work functions

Index Millikan reference Photoelectric effect

HyperPhysics***** Quantum Physics R Nave

Go Back

Early Photoelectric Effect Data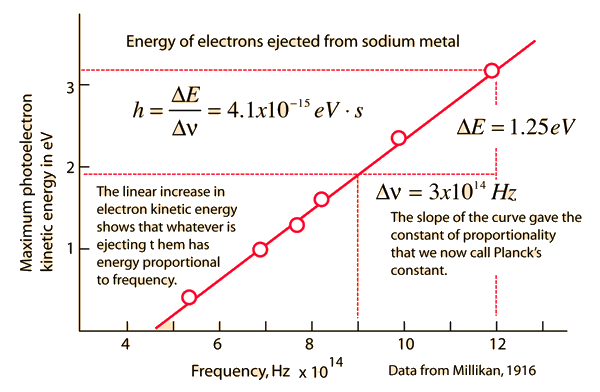 Planck hypothesis	Index Millikan reference Photoelectric effect
HyperPhysics***** Quantum Physics R Nave	Go Back

The Planck Hypothesis In order to explain the frequency distribution of radiation from a hot cavity (blackbody radiation) Planck proposed the ad hoc assumption that the radiant energy could exist only in discrete quanta which were proportional to the frequency. This would imply that higher modes would be less populated and avoid the ultraviolet catastrophe of the Rayleigh-Jeans Law.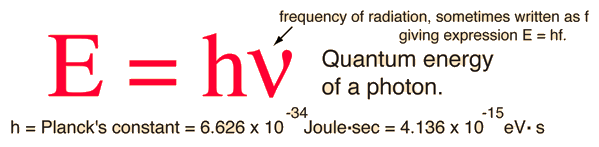 The quantum idea was soon seized to explain the photoelectric effect, became part of the Bohr theory of discrete atomic spectra, and quickly became part of the foundation of modern quantum theory. Calculation Interaction of radiation with matter Electromagnetic spectrum Basic quantum processes Are there limits on the frequency of a photon?

Index Photoelectric effect

HyperPhysics***** Quantum Physics R Nave

Go Back

Photon Energies for EM Spectrum Quantum energy hυ = x 10^ eV Quantum energy hυ = eV =MeV =GeV Wavelength x 10^m = m = nm = microns Frequency x 10^Hz = kHz = MHz = GHz = 1/cm (wavenumber) Planck hypothesis Interaction of radiation with matter Energies in electron volts Thermal energy for comparison	Index
HyperPhysics***** Quantum Physics R Nave	Go Back

Photons: The Quanta of Light According to the Planck hypothesis, all electromagnetic radiation is quantized and occurs in finite "bundles" of energy which we call photons. The quantum of energy for a photon is not Planck's constant h itself, but the product of h and the frequency. The quantization implies that a photon of blue light of given frequency or wavelength will always have the same size quantum of energy. For example, a photon of blue light of wavelength 450 nm will always have 2.76 eV of energy. It occurs in quantized chunks of 2.76 eV, and you can't have half a photon of blue light - it always occurs in precisely the same sized energy chunks. But the frequency available is continuous and has no upper or lower bound, so there is no finite lower limit or upper limit on the possible energy of a photon. On the upper side, there are practical limits because you have limited mechanisms for creating really high energy photons. Low energy photons abound, but when you get below radio frequencies, the photon energies are so tiny compared to room temperature thermal energy that you really never see them as distinct quantized entities - they are swamped in the background. Another way to say it is that in the low frequency limits, things just blend in with the classical treatment of things and a quantum treatment is not necessary. Thermal energy is the energy that comes from heat. This heat is generated by the movement of tiny particles within an object. The faster these particles move, the more heat is generated. 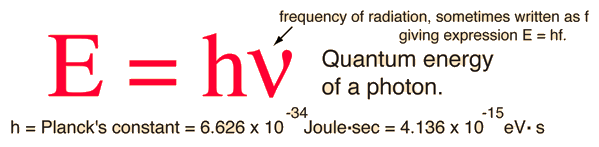Calculation Interaction of radiation with matter Electromagnetic spectrum Basic quantum processes

Index Photoelectric effect

HyperPhysics***** Quantum Physics R Nave

Go Back

[PDF]THE PLANCK SCALE

www.colorado.edu/philosophy/vstenger/.../PlanckScale.pd...

• 頁庫存檔
• 類似內容

翻譯這個網頁

the time, t, it takes for light to travel between the points in a vacuum, multiplied by a constant, c: ... Physicists and astronomers often work in units where c = 1, ... uncertainty in a measurement of energy in that time interval, AE, can be no less.

The temperature of photon and its energy

up vote5down votefavorite 3

Do photons have temperature? If not, does it mean that photon lose energy while travelling through space? As the planets farther away from the sun are comparatively cooler than the one that are closer to it, does it imply that photon also lose energy? thermodynamics energy photons temperature thermal-radiation share|cite|improve this question edited Nov 8 at 13:54 Qmechanic♦ 51.3k766170 asked Mar 30 '13 at 2:48 idiosincrasia23 58831226

I could have sworn we have a existing question on the smallest system to which thermodynamics could be reasonably applied, which I think is very much related, but I can't find it. – dmckee♦ Mar 30 '13 at 4:38 add a comment |

5 Answers 5

activeoldestvotes

up vote5down vote

This is really just an extension to JKL's answer since I wanted to pick up on his point about the microwave background, but first it's worth mentioning that although individual photons do not have a temperature EM radiation can be assigned a temperature. The EM radiation emitted by an object has a spectrum that depends on its temperature through Planck's law. So if you measure the spectrum of radiation it is sometimes possible to assign it a temperature through Planck's law, and indeed this is how the cosmic microwave background is assigned the temperature of 2.7 degrees. But back to the CMB: I would guess your question is asking if an individual photon can lose energy by radiating away like a cooling object, and the answer is no. However light can cool if the spacetime through which it is travelling is expanding. The light cools because it's energy is spread out over a larger volume of space. This is how the cosmic microwave background has cooled from it's original very high temperature of about 3,000K to its current value of 2.7K. share|cite|improve this answer answered Mar 30 '13 at 7:13 John Rennie 159k16271448

Indeed, the maximum in the spectrum connects the radiation wavelength, λ max   at the maximum, and temperature of the hot object as λ max T=2.9×10 −3   mK (Wien's Displacement Law). – JKL Mar 30 '13 at 20:33 add a comment |

up vote4down vote

The photons themselves do not have temperature as such. However, photons do contribute to the temperature of objects since they carry energy. A very good example is the microwave background radiation which is known to contribute a temperature to the universe at about 3K. One can work out the frequency of these photons using the basic relation k B T mwb =hf  where k B =1.381×10 −23   JK −1   and h=6.63×10 −34   Js, so that the requency turns out to be in the microwave part of the electromagnetic spectrum. Photons contribute to the temperature of your body when you sit in the sunshine and absorb the sunlight. The farther you go from the sun the cooler, correct, but this is because the intensity of solar light is inversely proportional to the square of the distance from the sun. On Earth we receive about 1350 W/m 2   of solar power. But on Mars, which is about 1.52 the Earth-Sun distance, it is only about 584 W/m 2   . share|cite|improve this answer answered Mar 30 '13 at 3:32 JKL 2,330413

add a comment |

up vote1down vote

Assume the sun emits a certain number of photons, such that, at 1m from the sun's surface 1 million photons go through each square meter. As the photons spread radially out from the sun, their number stays the same, but they have to cover larger and larger areas. At 10m from the sun, those 10 6   photons will cover an area of 10  x 10=100m 2   . So the density of the photons will be 100 times smaller than at 1 m. This shows how, as you travel away from the sun, the density of photons decreases inversely proportional to the square of the distance from the sun. That is what causes the temperatures of the planets to reduce with their distance from the sun. share|cite|improve this answer answered Mar 30 '13 at 10:05 hdhondt 3,1841411

add a comment |

up vote1down vote

At thermal equilibrium temperature T  is defined by 1T =∂S∂U   Where S  is the entropy and U  is the total energy. Since a system composed of photons has a well-defined energy and entropy, photons can be said to have a particular temperature if the whole ensemble could be in thermal equilibrium with some hypothetical environment. Planets further from the sun are cooler than close ones because the same photon flux is spread out over a greater area compared to the size of the planet: Earth's cross sectional area is a greater fraction of the surface area of a sphere the size of it's orbit than Neptune's for it's orbit. This means fewer photons per unit area hit Neptune than Earth. Photons do lose some energy going out that far (redshift from the sun's gravity, this is from general relativity), but this effect is tiny. share|cite|improve this answer edited Oct 21 at 23:53 answered Mar 30 '13 at 7:27 Dan 3,88321841

Can't a cavity in thermal equilibrium be looked upon as a gas of photons at some particular temperature? – Charuhas Mar 30 '13 at 12:59 @Charuhas: Exactly! – Dan Mar 30 '13 at 16:53 add a comment |

up vote-1down vote

Well it is not the total energy alone which determines temperature but the "quality" of energy as well. Temperature is a measure of average kinetic energy or also related to the wavelength of the photon. If you have enormous quantity of microwave range of photons the temperature anywhere may not rise above 3K. Classically and close to reality it is Weins displacement law that determines temperature in a spectrum.