"本征值是该力学量的宏观可就是宏观上测量该力学量的结果,就是微观上通过计算该力学量本征方程得到的本征值中的一个 。
道学文化的新科学观(上)
"另一个理论是多世界理论,是休·艾弗雷特三世(Hugh Everett III)在1957年提出的量子力学的一种解释。在量子力学中,我们知道,任何一个事件是否发生是有概率的,由波函数决定。传统的哥本哈根学派解释认为,当一个观测者作测量时,他以及仪器与被测量的系统发生相互作用,导致被测量的系统波函数发生塌缩,塌缩到某个物理量具有固定值的那个波函数。塌缩理论与量子力学的其他要素完全不同,是一种非幺正过程,或者说损失信息的过程。在艾弗雷特的解释中,波函数没有塌缩,每作一次测量,测量者和被测量者将处于纠缠态中,而且有无限多个纠缠态。测量一次,每个纠缠态都实现了,只是处于不同的世界。因此,这个解释叫做多世界解释。"
[PDF]有限耦合系统上的信息和能量的量子操控 - 中国科学院理论 ...
www.itp.ac.cn/~suncp/thesis/Hui_Dong_2011.pdf
[PDF]量子密码协议理论研究 - 国防科技大学
jpkc2010.nudt.edu.cn/xxlybmjc/introduction/wj/0.pdf
中國社會科學院哲學系教授
胡孚琛 教授
资料来源:哲学研究
21世纪的人类正处在一场新科学革命的前夜,这场革命必然也会在哲学领域发生。有趣的是,这场新科学革命将有可能再次回到曾经做出火药、指南针、造纸、印刷术四大发明的中国,向老子的道学文化汲取智慧。人们发现,21世纪的新科学将是整体的科学,是揭示宇宙、生命和心灵三者“大统一”规律的科学,这种新科学我们称之为新道学。
一
什么是道?老子《道德经》云:“有物混成,先天地生。寂兮寥兮,独立而不改,周行而不殆,可以为天地母。吾不知其名,强字之曰‘道’,强为之名曰‘大’。大曰逝,逝曰远,远曰反。”“道,可道,非常道;名,可名,非常名。‘无’,名天地之始;‘有’,名万物之母。”这两段话描述了三层意思,其一讲“道”是自本自根的宇宙最高的绝对本体;其二讲道不能用语言来描述,不能用人的感官或仪器直接观察,但却可以从“有”和“无”两个方面体认它的玄妙;其三讲道化生宇宙万物、宇宙万物又复归于道的“大循环”规律,是道“周行而不殆”的根本规律。由此可知,老子的道论把道当作哲学上永恒的形而上的最高本体,又当作科学上宇宙的起始点和终结点:道是自然界、生命界、人类社会、心灵世界等万事万物的总根源,并贯穿和永存于万事万物之中,是一切“存在”的根据。道是宇宙的本原,它有体有用。所谓道体,即是宇宙万事万物之原始本体,它呈现“有”和“无”两种状态的统一。首先是“无”,即宇宙创生之前的“虚无空灵”状态,称为“天地之始”,具有质朴性和绝对性。然后是“有”,即宇宙创生之际具有生化功能的全息的混沌状态,称为“万物之母”,具有潜在性和无限性。所谓道用,是宇宙所有运动和变化的驱动力,是创生宇宙万事万物的“合目的性”的模本,是宇宙的根本节律和法则秩序,是宇宙万事万物中普遍存在的客观规律,称为“常道”。
什么是道?老子《道德经》云:“有物混成,先天地生。寂兮寥兮,独立而不改,周行而不殆,可以为天地母。吾不知其名,强字之曰‘道’,强为之名曰‘大’。大曰逝,逝曰远,远曰反。”“道,可道,非常道;名,可名,非常名。‘无’,名天地之始;‘有’,名万物之母。”这两段话描述了三层意思,其一讲“道”是自本自根的宇宙最高的绝对本体;其二讲道不能用语言来描述,不能用人的感官或仪器直接观察,但却可以从“有”和“无”两个方面体认它的玄妙;其三讲道化生宇宙万物、宇宙万物又复归于道的“大循环”规律,是道“周行而不殆”的根本规律。由此可知,老子的道论把道当作哲学上永恒的形而上的最高本体,又当作科学上宇宙的起始点和终结点:道是自然界、生命界、人类社会、心灵世界等万事万物的总根源,并贯穿和永存于万事万物之中,是一切“存在”的根据。道是宇宙的本原,它有体有用。所谓道体,即是宇宙万事万物之原始本体,它呈现“有”和“无”两种状态的统一。首先是“无”,即宇宙创生之前的“虚无空灵”状态,称为“天地之始”,具有质朴性和绝对性。然后是“有”,即宇宙创生之际具有生化功能的全息的混沌状态,称为“万物之母”,具有潜在性和无限性。所谓道用,是宇宙所有运动和变化的驱动力,是创生宇宙万事万物的“合目的性”的模本,是宇宙的根本节律和法则秩序,是宇宙万事万物中普遍存在的客观规律,称为“常道”。
常道(或曰“常”)是宇宙一切生化运动的总规律和总原因,包括亚里士多德的动力因、形式因、质料因、目的因。世界各民族的先哲千百年来一直体悟和趋进某种无限本体,例如柏拉图的“最高理念”、普罗提诺的“上帝”、佛陀的“心”,直至18世纪黑格尔的“绝对理念”,而老子的“道”是人类智慧不可超越的最高宇宙本体。道既是宇宙的本原,又是人类的本我(真我)。作为宇宙的本原,道是一种绝对的真知,因而是为符号指称所难以描述的最终存在。语言符号的指称和数字只能描述相对知识,而道是只能体悟难以言传的绝对知识(智慧)。老子《道德经》云:“为学日益,为道日损。”人们学习各门科学知识,须不断积累,增强自己的“理性思维”能力,称之“为学日益”。人们要修道,则须不断排除世俗社会名利色权的干扰,逐渐放下自己内心的各种执著,开发自己“灵性思维”的智慧,谓之“为道日损”。前者为“知识”的积累,靠的是“理性思维”后者为“智慧”的创发,靠的是“灵性思维”,得道就是求得大彻大悟圆满无碍的大智慧。作为人类心灵的本我(真我),道是“知觉者”,因而具有不可被知、不可当作测量和计算的对象,即“不可名”、“不可道”的性质。道是自本自根、自生自化的无分别相,因而具有不能被创造、不能被区分的性质,是宇宙创生之前的“无极”状态。
二
老子《道德经》云:“道生一,一生二,二生三,三生万物。万物负阴而抱阳,中气以为和。”这段话是新道学文化的宇宙创生和演化图式。它的意思是说,宇宙间万事万物据其“全息原理”皆开端于一;万物都是阴阳互补的统一体,遵循阴极生阳、阳极反阴的“太极原理”。
“道生一”中的“一”,在道学中指元始先天一,是宇宙创生之始的一片混沌状态。它是宇宙初始状态下隐藏着的秩序,是产生宇宙根本节律的信息源。“一”是最初的宇宙蛋,是种子,是原型,是基因,是宇宙中万事万物全息的“模本”。天下万事万物都有一个最初的全息“模本”,都是由“一”开端,掌握了开端的“模本”,由此展开,就掌握了事物整个过程的要害。
“一生二”中的“二”,指阴阳二性,即易学中的“两仪”。道学中的“阴阳”,即黑格尔所谓普遍存在的“矛盾”,即马克思描述的“对立统一”规律,也即恩格斯所谓引力和斥力、正物质和反物质的相互作用状态。“二”中隐含着宇宙创生和演化的涡旋式的内在驱动力。在科学上,“二”即量子场理论中的“零点场” (zeropoint field)、“费米子真空” (fermion vacuum)或“狄拉克海”,也就是欧文•拉兹洛描述的那种“量子虚空全息场”,或称“挠场”(又译“扭力场”)。道学的“二”是各向同性的“标量场”,而“三生万物”是“矢量场”。
“二生三”中的“三”,是指有象、有气、有质的信息、能量、物质三大要素。物质是宇宙以粒子性存在的方式,它标志着部分和整体、个别和一般之间的区别;能量是宇宙以波动性存在的方式,它标志着运动和静止、间断和连续之间的区别;信息是宇宙以选择性存在的方式,它标志着有序和无序、方向性与合目的性。必须指出,物质、能量、信息都是可分为不同层次和不同形态的,人的心灵则是信息的最高形态。
“三生万物”,就是说宇宙从无机界到有机界,从生物界到人,都是由信息、能量、物质三大基本要素组成的。当量子虚空全息场的基态受到“激发”,打破“虚无空灵”的虚时间和虚空间,标量场在涡旋中变为矢量场,能量和物质也脱离潜在的“虚”状态,信息则呈现为物质和能量的形式或结构。“三生万物”是宇宙大爆炸的起始点,宇宙由此从先天突变为后天,现实世界的万物由信息、能量、物质因缘和合而生。必须指出,信息、能量、物质这三大要素皆没有西方哲学中“实体”的机械论含义,而是有如佛陀的缘起法所说的那种“关系”的实在,是这些实在的“关系”生成“万物”,物是缘起于这三大要素的“关系”的。因之道学所谓“生”,皆“依缘而生”、“因缘所生”。
当代中国哲学界一些学者将老子哲学中“三生万物”的“三”解释为阴气、阳气、冲气,这是对老子的天才智慧的曲解。“三”为信息、能量、物质三要素,这是老子智慧的真义。“万物负阴而抱阳”是道的“太极原理”;“中气以为和”是德的“中和原理”。根据道的“生化原理”,宇宙中万物无阴阳不生,无阴阳不化,一阴一阳之谓道,阴阳平衡之谓德。世界上万事万物都有在不断震荡、螺旋式变化和发展的运动中最终靠向中和态的趋势,中和态即阴平阳秘的稳定态。
三
1980年,我发现了一个新的物理常数H,其数值等于玻尔兹曼常数k和自然对数ln2之积,并推导出“可用能”与“信息”之间相互转化的数学关系式,现将其基本内容介绍如下:
科学史上力学和热学曾经分家达一个世纪之久,这并不是因为力学家一点也看不到热现象往往伴随着力现象以俱生,而只不过是因为他们认为这不在其研究范围之内罢了。在过去百余年中,热力学家不注意信息,似乎是这一现象的历史重复。既然过去把力学和热学结合起来曾经改变了整个力学的面貌,现在如果我们直接把信息引入热力学,也必将大大开阔人们的眼界,从而促使热力学和信息论在科学史上趋向统一。
我们不难理解,热只能从高温传向低温,这首先是因为消除了热传导方向上的不确定性,产生了信息。物理系统的自发不可逆过程,也是因为不同过程留下了不同的痕迹,付出了依赖过程变化的信息量。世界上任何自发过程都是不能不留痕迹的,它不能自动复原正是因为它在外界残留下信息。其实,任何热力学过程都伴随着信息的变换和传递,只不过这一点以前长期被人忽视而已。所谓第二类永动机,是想不付出能量的质在信息传递中发生退化的代价而白得到功,当然是不可能制造的。太阳的热辐射,是一种熵增过程,同时这种辐射又是地球上信息的来源;如果太阳熄灭,地球上的生命马上终止。当两个氢原子核聚合时,总质量的一部分转化为进入恒星外层空间的辐射能(根据爱因斯坦公式E =mc2),这些能量也携带了一定的信息量,使整个过程的熵也增加了,因为束缚在原子核内的能量向空间传播这一过程可以被认为是无序程度增大。由此可知,在宇宙中,不和信息相联系的纯粹能量变化是没有的。
我们知道,一个热力学系统中的内能U只有一部分可以产生机械功,这一部分叫作可用能E。在孤立系统的等温变化中,可用能也就是自由能,这时系统内部有均匀的温度T,据热力学第一定律,当系统的温度与四周温度趋于相等时,E =U - JTS。J为热功当量,JTS也叫束缚能。既然束缚能和熵的联系早已明确,那么可用能和信息的联系能否给出呢?
我们已知信息量I和热熵S的关系式为:
I =(Smax - S)/(k ln2)
Smax为系统最大可能的熵,S为系统的实际熵。如果把Smax和S分别用物理系统的理想气体在可逆过程的热温商和在等温膨胀达到平衡时的实际热温商来表示,则
由于ΔQ在这里表示恒温条件下可逆过程吸收的热能和不可逆过程吸收的热能之差,我们知道,最大功只能在可逆过程中得到,不可逆过程等于浪费了功,ΔQ实为不可逆过程浪费的可以用来做功的可用能E。于是,我们推演出信息量I、可用能E和绝对温度T的关系式:
E =H IT
当信息量的单位取比特(bit),H = 0. 975×10- 16尔格0 K- 1,为玻尔兹曼常数k和自然对数ln2之积。这样,信息和熵不仅在统计学的概率表达形式上是一致的,而且在物理内容上和能量的联系形式也是对应的。上式的物理意义是:
热力学系统储存的信息量I和该系统的可用能E成正比,和其绝对温T成反比。
这样,结合第一定律,我们还可得到下面孤立系统内能、信息转化和守恒的关系式:
U =H IT + JTS
这说明在系统的内能不变时,要增加能量的信息储存,就需要做功以减少系统的熵,使其可用能增加。反之,在系统的熵增加时,可用能就减少。在自然界天然变化中发射自由信息的熵增过程,都是可用能减少的过程。这时系统的内能在量上虽然守恒,但在质上要发生退化,可用能会转化为束缚能。热能的价值决定于它所能产生的功有多少,当系统的熵增加时,热能的价值便降低,变得愈来愈不中用。由此看来,熵不但是热分子混乱程度的标志,而且是能的不可用程度的量度。反之,信息则是系统结构的有序性及其能量的有序性或可用程度的量度。这样,我们就可弥补原来能量只从量上量度的缺陷,给出能量从质上比较的标准。宇宙中万物的熵自发增加的趋势,同时也决定了它们在相互作用中自动发射信息的属性。孤立系统的内能和信息是守恒的。
上述观点完成了一项本来应该在19世纪由玻尔兹曼作出的科学结论,在现代物理学家早已视为经典的热力学定律中打开了缺口。实际上,19世纪至20世纪奠基的物理学大厦并非无懈可击,其中有几个重要的关系式和物理常数的发现透露出自然界更深层的奥秘,它们包括:普朗克常数h,玻尔兹曼常数k,光速C。海森堡测不准关系式:(1)能量和时间ΔE•Δt≥h,(2)位移和动量Δx•ΔPx ≥h。还有两个基本关系式:(3)E =mc2 ,(4)E = hυ。将(3)、(4)式联系起来得到(5)m = hυ/ c2 (包括物质波公式λ= h /mυ)。
再结合我给出的信息和能量关系式(6)E =H IT,可以得出结论:
这样,我们再把虚数i代入到这些关系式中,采用求极限(n→±∞,n→0)等数学运
宇宙中的信息、能量、物质是可以按一定数学关系相互转化的,它们在孤立系统中是守恒的。这就推导出新道学的宇宙中物质、能量、信息相互转化和守恒定律。
算方法,将其扩展到无限大的宇观宇宙或无穷小的微观世界(包括虚世界),就可推导出一些有重大物理意义的新关系式,解决科学界很多悬而未决的物理难题。我们由此指出,一些最小最轻的基本粒子(特别是玻色子)必然同时具有波动性、粒子性、选择性三种基本特征。通过科学实验不仅可以证实这些基本粒子具有波粒二象性,而且可以证实它们存在物质(粒子性)、能量(波动性)、信息(选择性)三象性。选择性本质上是一种心灵特征,宇宙小至基本粒子大至银河系,自创生起就有“合目的性”的选择趋势。基本粒子携带的信息就是一种“原初的心灵”,由基本粒子进化成原子、分子、有机物、细胞、生命体直至人的大脑,信息组合的层次越来越高,进化至最高层次则为人的心灵。这就是说,宇宙从基本粒子到星系团本身都是有生命的和有心灵的,宇宙的演化和生命的进化都是“合目的”的,因之,地球上生命现象的出现和人类心灵的花朵盛开决不是偶然的!道学一直将宇宙视为一个生生不息的大生命体。宇宙本身是一个有“记忆”、会“学习”的全息的超巨系统。欧文•拉兹洛《微漪之塘》中讨论的“量子真空零点全息场”,实际上是以“灵子”为中介的“灵子场”的衍生物。“灵子”为心灵信息的“载体”。新道学的宇宙图景消除了西方哲学笛卡尔心和物二元论的对立,给出了心、物、能一元论的宇宙观。
保守力和非保守力
保守力和非保守力
高雄市中正高工物理科代理教師、現任聯華電子工程師 蘇益弘
高雄市中正高工物理科代理教師、現任聯華電子工程師 蘇益弘
本文將循序漸進,從國中、高中、大學的角度說明保守力和非保守力,重點以紅字與粗體先行標示,緊接著的後文則進一步說明。以下是本文大綱:
- 通俗的說法,以國中的角度來看保守力和非保守力
- 嚴謹的說法,以高中來說,我們要知道的保守力和非保守力的定義
- 數學的說法,以大學來說,你會以數學(微積分)的角度重新了解保守力
- 國中角度來看保守力和非保守力
- 保守力:作功可以轉換成位能儲存,非保守力:沒有位能的概念,自然也談不上位能的儲存。
- 物體只受保守力,力學能守恆。物體受到非保守力,力學能通常會損耗。
所以,保守力指的是對物體作功後可以轉換成位能儲存的力。前一段講的,物體越高能量越高(重力位能U=mgh),隱含了重力是保守力這個概念。彈簧越緊能量越高(彈力位能U=1/2kx2),彈簧力也是保守力。而相反的,如摩擦力就無法討論對應的位能,因為這個力做了功之後化成熱能,結果我們無法把此能量取回來、重新做功。因此,摩擦力非保守力。你平常在推東西的力,也不是透過體內儲存的某種位能之改變而造成,所以它也是非保守力。下面整理高中常見保守力的實例:
保守力:重力、彈簧力、靜電力
非保守力:摩擦力、阻力(空氣.水)、推力、拉力
再來看第二點。國中時候的你一定有學過力學能守恆。先釐清它跟能量守恆有什麼不一樣?讓我們複習下,力學能=動能(K)+位能(U)。所以它指的是單純力學運動中會碰到的能量,我們不考慮電能.熱能.化學能…等,那是能量守恆要去想的事。
所以力學能要守恆,代表動能+位能要固定,代表受力過程中動能位能要能互相轉換。代表受力做功要能儲存成位能,也就是受到的力是保守力。舉個例,像重力。想像小球從高處落下時,高度越低(位能下降)、速度越快(動能上升),這是位能轉動能,力學能守恆。或者往天空用力丟小球,高度越高(位能上升)、速度越慢(動能下降),這是動能轉位能,力學能同樣守恆。而如果受的是非保守力,那只會損耗力學能而不會守恆。像摩擦力,一個小球在地面滾動,速度越變越慢,但高度不變,只會有熱散失到空氣中(動能轉熱能)。
下面我們看個你一定很熟悉的題目:有一個靜止小球10kg在10m高的台階上,當受到重力順著斜坡(光滑無摩擦)滑下來,到達地面時速率多少?(圖一)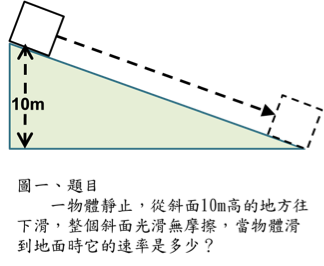

簡單吧,是不是很熟悉的用K初+U初=K末+U末,然後答案解出,輕鬆得分。這裡用的觀念就是力學能守恆,但它有兩個前提,受到重力跟光滑無摩擦。力學能守恆的前提就是:你受到的力要是保守力才會力學能守恆,如果是非保守力則否。所以整個過程只受重力(保守力),而沒有非保守力(摩擦力),所以可以用力學能守恆。如果題目說斜坡是粗糙有摩擦,則非保守力(摩擦力)會造成力學能損耗,就不能用K初+U初=K末+U末去算,必須另外計算摩擦力做功造成多少損耗。下面補充箱子受力圖,與各力的作功。
到這邊再重新歸納一次。保守力:有位能,力學能守恆,重力,彈簧力都是。非保守力:沒有位能,力學能通常會損耗,推力.摩擦力.阻力都是。這些是比較通俗的講法,下面我們講講較嚴謹的定義。 - 高中須知道保守力的定義
- 一個力對物體作功,經過一段路徑,從A點到B點。如果作功大小與經過路徑無關的是保守力,有關的是非保守力。
- 一個物體從A點出發,經任一路徑又回到原點A,我們稱此為封閉路徑。如果力對物體作功,經任一封閉路徑後,總作功恆為0,則此力為保守力。
什麼叫作功與路徑無關?請看圖三,物體從A點到B點有三個路徑1、2、3,如果對物體施力走這三條的做功都相同,代表作功與路徑無關,這種力就是保守力。反之則為非保守力。
下面讓我們分別以重力(保守力)、摩擦力(非保守力)做例子,用簡單的題目和數字來算算看,什麼叫與路徑無關。
重力(保守力):題目:今天有一個箱子重量mg,小明把它抬高d公尺。小華無聊又白目,所以他抬高箱子d公尺後又把它放到地上,再抬一次。請問這兩種過程中,重力對箱子的作功各是多少?
解答: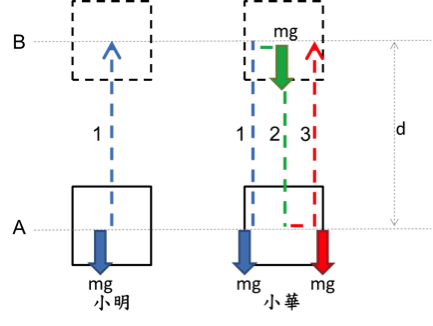

先講一點,在這裡箱子往上抬的過程(位移1、3),因為重力往下位移往上,方向相反,所以作的是負功(W1、W3)。
那注意到裡面的運算嗎?雖然小華比小明多抬了一下,但因為重力一直是向下的,所以箱子被放下時重力作正功(W2),抬起時作負功(W3),放下和抬起的作功剛好抵銷。即使小華今天想勤練肌肉,把箱子抬上抬下N次,總重力作功(W華)一樣是 – mgd,箱子本身的高度就只會上升d,不會有更多位能。只要箱子是從A點移到B點,不管過程中箱子被抬多少下,重力作功都相同,與過程路徑無關,所以重力是一種保守力。
摩擦力(保守力):題目:同樣的明、華二人組。今天小明把開學裝書的箱子從樓梯口推到A教室門口(與樓梯口相距d公尺)。情竇初開的小明,偏偏要把箱子推到隔壁教室B(與教室A相距d公尺),看一眼最愛的阿花,再把箱子推回A教室門口。請問這兩種過程中,摩擦力(fk)對箱子的作功各是多少?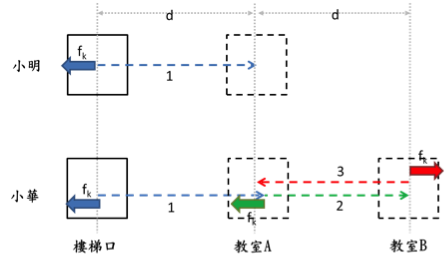

同樣提醒一點,在這裡摩擦力和位移都是反方向,不管位移1、2、3,摩擦力都作負功(W1、W2、W3)。
從運算裡可以看到,因為摩擦力一直作負功,所以小華推去B教室又推回A教室的途中(W2+W3),摩擦力作的功不會像重力一樣抵銷,而是產生更多的負功。小華只要夠無聊,他每多推一次摩擦力就會多作–2fkd,這部分能量會轉變成熱能散失在周遭。結論:同樣是箱子從樓梯口到教室A,但只要繞的路徑越長,摩擦力作功就越多。摩擦力做功與過程路徑有關,所以摩擦力是非保守力。
那在最後,我們把定義換個說法來複習一下。保守力做功大小只和移動的初位置和末位置(位移)有關與移動路徑無關,而非保守力做功大小則要考慮物體走的是哪條移動路徑。
到這邊我們已經了解高中保守力需要知道的東西了,但我們只要上網路一查,常會查到一些不熟悉的數學符號,這部分是在大學學會微積分後,我們就可以用數學(微積分)去把保守力作定義。下面我們不談數學,只簡單講講這些數學在表示什麼物理意義。 - 數學上保守力(F)的定義
第一點,F的旋度是0,旋度這東西很特別,它指的意思就是這個物理量(F)他會圍繞著一個點旋轉(通俗的說法)。舉個熟悉的例子,我們國中有學安培右手定則:一個通電流的導線,它周遭會有同心圓旋轉的磁場。所以對於這根導線來說,磁場是圍繞著它旋轉,這個磁場就有旋度(相對於導線)。如果世界上有一種力的分佈就像上述磁場一樣,則此力就不可能是保守力,因為沿圓周繞一圈回到原點後,此力會做淨功。這與前面提到的定義2,封閉路徑作功為0不符。做因此,保守力的條件就是旋度為零。
第二點,這應該很熟悉吧。沒錯,它就是高中我們學到的定義2,只是用數學形式表示。
第三點,這其實剛剛也提到,它是國中說法裡面的第一點,只要是保守力就會有對應的位能,Φ代表的就是位能。這個式子只是換句話說,你一定找得到一個位能Φ,他的梯度能對應到保守力(F)。特別提一下這裡的負號,我們高中會學到重力位能差的定義:重力位能差等於負的重力做功。這邊的負號代表的就是位能差定義裡提到的負的。
以下補充解釋下梯度,梯度是描述物理量(Φ)的陡峭(變化)程度。這個式子說的是,今天你有一個位能Φ (假設是重力位能),那位能的梯度基本上就是物體所受到的力(亦即,算重力位能的梯度就可得到重力)。倒過來想更好理解,今天你抬物體上升一固定高度h,那物體的重力位能一定是變大了。既然高處的位能Φ高處大於低處的位能Φ低處,Φ顯然是有一個梯度(=(Φ高處-Φ低處)/h)。由於Φ高處-Φ低處就等於你以力量F (恰等於重力)去抬高物體所做的功F·h ,因此的Φ梯度就是F。
对一个粒子的空间波函数进行
某种测量时,塌缩将导致其空间波函数的改变,比如
从ψ(x) →φ(x) . 显然,这是涉及整个空间分布的改
变,而不是局域变化和局域变化在空间中的传播. 就
是说,这里同样也不存在局域发生的“空间波函数的
塌缩波”的“空间传播”,而是一种全空间的、瞬时的、
不可阻断的、也就是超空间的突变. 据此完全可以
说,空间波函数测量所产生的塌缩同样也具有非定
量子测量与时空塌缩
X
张永德
(中国科技大学近代物理系, 合肥, 230026)
摘 要 在综述量子Zeno 效应和量子态超空间传送(它包括量子Teleportation 和Swapping) 的同时, 着重
分析了它们与量子力学基本原则以及时空性质之间的关连. 强调指出,量子测量将导致空间广延性的消失和
时间流淌性的停滞,而所述的三个奇妙量子现象正是这种时空塌缩的物理表现.
关键词 量子Zeno 效应; 量子Teleportation ; Swapping
中图分类号: O413 文献标识码: A 文章编号: 1005 - 7188 (2000) 04 - 0187 - 07
1 量子测量理论摘要
量子测量理论十分庞杂、异常丰富,未解决的问
题很多,成为量子理论中最重要的悬而未决的问题.
这里根据本文的需要,作为引言仅阐述它的轮廓和
摘要论述其中最基本的问题. 事实上,这里涉及的许
多问题,诸如,测量中量子熵的改变、测量中时间不
可逆问题、塌缩的非定域性、塌缩随机性的本质、量
子力学的双重因果性问题、广义测量和混态系统演
化的各种理论、各种类型的非完整的量子测量等等,
都是有待研究的问题.
1. 1 量子测量公设———量子力学第三公设
1. 1. 1 量子力学5 大公设:
量子态公设
力学量算符公设
量子测量公设
量子态演化方程公设
全同性原理公设
1. 1. 2 量子测量公设
对任一(归一) 量子态|ψ〉观测力学量A ,相应于
将被测态|ψ〉按A 的对应厄米算符^A 的本征态族{|
ψn〉| ^A|ψn〉= an|ψn〉}展开
| ψ〉= Σn
Cn | ψn〉; ( Σn
| Cn | 2 = 1)
单次测量中所得A 的数值可能不确定, 但必为算符
^A 本征值{an}中的一个;多次测量所得A 的平均值
为
珔Aψ ≡〈ψ| ^A | ψ〉= Σn | Cn | 2 an ,
其中, A 取an 值的几率为
Pn =| Cn | 2 .
测量完成之后,系统即以塌缩后的态为初态,在测量
后的环境中作新一轮演化.
1. 1. 3 附加分析
a) 若| ψ〉是^A 的一个本征态,展开结果只有一
项,相应测量结果就是确定的.
b) 测得的所有an 和珔Aψ 值均是实的;
c) ^A 、^B 可同时测量的条件为[ ^A , ^B ] = 0
此时,力学量A、B 之间不存在量子因果关系]
量子测量互不干扰;
d) {|ψn〉}的完备性与A 的可观测性之间的关
系:
“(物理实验上) 力学量A 是可观测的”等价于
“(数学上) 算符^A 的本征矢族是完备的”. 因为, 只
当^A 的本征矢族完备, 才可以对任给的被测态作谱
分解,如此才谈得上对其进行关于A 的观测;能对任
意态进行关于A 的观测,才可以说力学量A 是可观
测的[1 ] .
1. 2 量子测量理论纲要
1. 2. 1 量子测量过程的三个阶段[2 ] :
量子态谱分解
(| ψ〉= Σn
Cn | ψn〉) ;
将被测态按所测力学量算符本征态族展开———|ψ〉
187
X 收稿日期:2000 - 07 - 30
作者简介: 张永德(1939~) ,男,安徽人,教授,博士生导师, 奥地利科学院外籍通讯院士,中国量子力学研究会理
事长. 主要从事近代量子理论及其应用和近代量子场论中的数学问题的研究.
第9 卷第4 期
2000 年10 月
云南民族学院学报(自然科学版)
Journal of Yunnan University of the Nationalities (Natural Sciences Edition)
Vol . 9 No. 4
Oct . 2000
相干分解(保持原有相干性)
量子态坍缩
( Pn =| Cn | 2 , | ψn〉) ;
坍缩是一次斩断原有相干性的、随机的“选择”(“投
影”) (详细见下)
初态制备
(| ψn〉=| ψ(0) 〉) ;
坍缩制备初态(在新^H 下,开始一轮新的演化) ;但
制备初态并非必定要通过塌缩
1. 2. 2 量子态坍缩(Collapse , reduction) 的四大特
征[3~4 ] :
a. 坍缩结果的随机性 (非本征态) 单次测
量结果的不可预测性. 这是原则性的,并非量子力学
描述不完备的体现.
b. 坍缩总是斩断相干性的 坍缩不继承位
相,坍缩是一种“投影”(Von Neumann) ,是一种“选
择”(Feynman) ———它破坏旧的相干性,建立新的相
干性.
c. 坍缩方向的不可逆性 是量子理论中唯一
体现“量子时间之箭”的场合. 坍缩使上一代的熵增
加,下一代的熵减少. 微观世界的总熵不会因大量不
断的量子测量而改变.
d. 坍缩总是非定域的. 因为
空间波函数坍缩: (ψ(珋x) →φ(珋x) ,由于珋x: 全空
间,所以是全空间的同时塌缩.
自旋波函数坍缩:自旋态本来就不含位置变数,
当然也是全空间的同时塌缩.
虽然量子测量通常是局域的,但它造成的坍缩
总是全空间的.
1. 2. 3 量子力学因果关系的两种形式[3~4 ] :
a. 决定论性的因果关系:
态的第一类变化———Schrodinger 方程演化:
“初条件|ψ(0) 〉+ 哈密顿量^H ”决定论,可预
测, 可逆,保持相干性,定域性.
b. 统计性因果关系:
态的第二类变化———测量造成的坍缩:随机性、
不可逆性、斩断相干性、非定域性. 两者的有机结合
构成量子力学的因果论.
1. 2. 4 测量的地位:
a. 什么情况的相互作用就算作量子测量———
如果此相互作用的结果是向某一力学量本征态塌
缩,这种相互作用过程便可以看作是对这一力学量
的量子测量过程.
b. 把测量仪器也包括进来作统一描述———从
量子信息论的角度来看,这个“测量仪器”是广义的.
它包括被我们(不得不) 忽略掉的系统的其余部分
(其余方面) 或是另外相关的更大系统. 统一描述的
结果将会产生许多新的情况,所以十分重要. 这方面
有大量的叙述,其中较早的一个便是下面关于量子
测量的Von Neumann 模型.
c. 微观的量子系统\宏观的测量仪器
1. 3 Von Neumann 正交测量模型[5 ]
为了测量子系统的可观测量A ,要修正“世界哈
密顿量”. 办法是连通子系统的可观测量A 和(作为
测量仪器的) 指示器X. 在A 和X 之间的这种耦合,
在可观测量的本征态和指示器的可区分态之间建立
起量子交缠,正是这种量子交缠,使我们能够通过观
测指示器变数X 去制备可观测量A 的本征态.
设初始时刻子系统处于A 的一个叠加态| ψ〉
= Σn
an | an〉,而指示器波包的关于X 变量的状态
为| ψ( x) 〉, 它们合成的大系统处于尚未交缠的可
分离态,
|ψ〉á |ψ(x) 〉= Σ
n
an| an〉á |ψ(x) 〉(1 - 1)
由于“世界哈密顿量”中A 和X 的耦合项存在,在t
时刻后,这个量子态将从可分离态演化成为交缠态,
U ( t) { Σn
an | an〉á | ψ( x) 〉} = Σn
{ an | an〉
á | ψ( x - λant) 〉} (1 - 2)
这种交缠使指示器的位置变量X 的数值和可观测
量A 的数值(即x 和an) 关联起来. 如果位置变量X
的观测精度足以分辨A 的全部本征值, 就实现了通
过测量X 的值来给出A 的相应本征值. 因为,测得数
值( x - λant) 的同时,将造成关联塌缩并给出A 的本
征态| an〉.
一个典型例子是Stern - Gerlach 装置, 为测1
2
自旋粒子的σz ,使它通过一个z 轴方向非均匀磁场:
Bz = λz . 粒子磁矩μ珋σ,它和磁场之间的耦使项(“世
界哈密顿量”中的耦合项) 为H′= - λμzσz . 这里是
可观测量σz 和位置z 相耦合. 由于H′中含z ,不同z
值处附加能数值不同,这产生一个力
F = -
5 H′
5z
= λμσz (1 - 3)
188
云南民族学院学报(自然科学版) 第9 卷
它沿z 轴,正负视σz 值而定. 于是在测量时间Δt 内
ΔP = FΔt (1 - 4)
这种耦合将传送一个冲量给粒子—指示器. 由此,可
以通过观察粒子向z 轴正向、反向的偏转,来投影给
出粒子自旋态| ↑z 〉或| ↓z〉, 从而测知可观测量
———粒子的自旋. 这里U(t) = exp{
i¶
λμzσzt} ,而
U(t) {[ Σ
2
i =1
αi | i〉] á | 0〉位置指示} = Σ
2
i = 1
{αi | i〉á |
hi〉位置指示} (1 - 5)
这里| hi | ≈ P
m
Δt ≈ FΔt2
m
.
小结上面Von Neumann 模型的基本思想:正是
被测系统和测量仪器的相互作用,造成两者的量子
纠缠. 于是,由测量仪器读数导致的仪器状态塌缩,
会使被测系统关联塌缩并给出被测力学量的一个本
征态,从而得到相应的本征值. 最后应当指出,Von
Neumann 模型有其局限性:它仅限于正交(投影) 测
量,这只适合于孤立量子系统的测量. 如果对一个含
有子系统的更大系统进行正交测量,这时在它的某
个子系统上所实现的投影操作(或直接对一个大系
统的一部分进行测量) 称为对这个子系统(一部分)
的广义测量. 一般说,广义测量不一定是正交(投影)
测量. 严格说来,所有能够实际实现的量子测量都应
当是广义测量.
2 量子力学的非定域描述与量子态塌缩的
非定域性质
2. 1 什么叫非定域性和非定域描述
研究微观粒子状态及其运动中,采用时空变数
x = (珋x , t) 对它们所作的描述, 称为对它们的定域
描述. 一个相互作用物理过程,如果它的进行依赖于
时空变数并且只和当时当地的时空变数(至多包含
无限小邻域) 有关,就称它为定域的物理过程, 表明
它不仅是一个时空中的过程, 而且是一个集合着局
域作用的定域过程. 比如,电磁波波包在时空中的传
播就是一个定域的物理过程, 对它有时空传播过程
的描述就是定域的描述. 再比如,两个粒子a 与b 的
相互作用,按量子场论的观点, 正比于它们(与粒子
相联系) 量子场A ( x) 和B ( x) (或其导数) 的乘积.
这样一来,在时空点x 处的相互作用就只依赖于x
点的A ( x) 与B ( x) (及x 点的无限小邻域) ,而与其
他时空点x′上的A ( x′) 和B ( x′) 无关. 这就是一个
定域的相互作用过程, 对它的描述也是一个定域的
描述. 这里面包括了,将粒子a 的量子场写为A ( x) ,
使得我们有权利说“在x 点上a 的场量”等等,这本
身就是一种定域的描述.
在物理学中,包括在量子理论中,几乎都是定域
的描述. 有没有非定域的描述呢?有. 通常所说的,对
某种性质的非定域描述,区分为两层不同的含义. 其
一,带某种弥散性的描述:对过程的描述还是借助时
空变数进行,只是此时的描述是对时空变数的某种
弥散(比如, 相互作用带某种积分核的时空积分变
换) ,使得在x 处的相互作用也以一定方式在一定程
度上依赖于别处x′的场量. 其二,拓扑性描述:在一
个势场中,粒子所受的力常常以势场的各类微分量
来表示,微分量的计算总是在局域范围内进行的,只
能涉及场的局域性质; 但这个势场也许还有非平庸
的整体性质,这是场的非局域性质,是一类难以用定
域描述方式确切表达的拓扑性质. 例如双缝干涉实
验中,设想紧靠缝屏之后放置一根无穷长细螺旋管,
管中产生一束细磁弦, 其作用是改变屏后空间矢势
场的整体拓扑性质:从曲面单连通区域变为曲面多
连通区域. 这使相因子只依赖于从磁弦的上方还是
下方绕过,而不依赖于上方或下方路径的种种具体
变形,因为在磁场强度为零的区域,路径可以连续变
形,而不会影响位相. 再比如,粒子的自旋态,由于它
直接依赖于联立的量子场方程的旋量结构而并不直
接依赖于空间变数(在非相对论量子力学中,由于常
常可以直接分离出自旋波函数, 对此看得更为清
楚) ,从而它表现出是旋量场的一种非定域的性质,
这是一种我们尚未从实质上把握的拓扑性质, 简单
说就是一种未知的超空间的性质(尽管我们早已知
晓它的运动规律) . 还可参见下节讨论.
2. 2 自旋态及其塌缩的非定域性质
EPR 佯谬的分析清楚显示,构成自旋EPR 对的
两个反飞行的粒子,经过足够长的时间之后,它们的
空间波包肯定已不再交叠,但它们的自旋态依然彼
此关联,各自的自旋取向均依赖于对方而处于一种
不确定的状态上. 这种关联是一种不依赖于空间变
数的关联,一种非定域的关联,一种超空间的关联.
一旦对其中某一粒子进行自旋取向测量,使其产生
塌缩,比如塌缩向上,则另一粒子虽处于遥远而未知
的地方,也将瞬时地发生自旋态朝下的塌缩. 这里不
存在什么“自旋态塌缩波”的“空间传播”,而是发生
着一种瞬时的、非定域的、不可阻断的、也就是超空
间的关联塌缩. 上面已经指出,这种非定域的关联塌
缩揭示出自旋态的拓扑性质. 它最清楚地表明了,自
旋和自旋态是该粒子的量子场的一种整体拓扑性
189
第4 期张永德: 量子测量与时空塌缩
质,是不能以定域的方式加以描写的. 从空间定域的
观点来看,由于测量导致非定域自旋态的塌缩,它把
空间的广延性也塌缩掉了.
2. 3 空间波函数塌缩的非定域性质
如果说,自旋态及其塌缩的空间非定域性质早
已为人们所注意的话,空间波函数塌缩的非定域性
质还远未引起人们应有的重视.
事实是,当人们对一个粒子的空间波函数进行
某种测量时,塌缩将导致其空间波函数的改变,比如
从ψ(x) →φ(x) . 显然,这是涉及整个空间分布的改
变,而不是局域变化和局域变化在空间中的传播. 就
是说,这里同样也不存在局域发生的“空间波函数的
塌缩波”的“空间传播”,而是一种全空间的、瞬时的、
不可阻断的、也就是超空间的突变. 据此完全可以
说,空间波函数测量所产生的塌缩同样也具有非定
域的性质.
3 量子Zeno 效应和量子力学公设之间的关
连———时间均匀流淌性的停滞
3. 1 含时系统初始衰变率的一个普遍结论[2 ]
对于包括粒子衰变在内的任何含时系统,一般
可写成(¶ = 1)
i
d | ψ( t) >
dt
= H( t) | ψ( t) >
| ψ( t) >| t =0 =| ψ(0) >
(3 - 1)
可以普遍证明:任一含时系统初始时刻的衰变
(或跃迁) 速率必为零. 就是说,有
dP( t)
dt
| t =0 = 0
P( t) =| < ψ(0) | ψ( t) >| 2
(3 - 2)
这里, P( t) 是演化到t 时刻系统仍存活(或保持) 在
初态的几率.
证:由于
d | ψ( t) >
dt
=
1
i
H( t) | ψ( t) > 和d < ψ( t) |
dt
= - < ψ( t) |
1
i
H( t)
于是
dP( t)
dt
= < ψ(0) | {
d
dt
| ψ( t) >} +{
d
d
< ψ( t)
| } | ψ(0) > =
1
i
< ψ(0) | H( t) | ψ( t) > -
1
i
<
ψ( t) H( t) | ψ(0) >
令t →0 取极限,即得
dP( t)
dt
| r =0 = 0 (3 - 3)
这是含时系统的一个普遍结论,当然也是各类
含时微扰论的共同特征. 从表面上看,这里的量子力
学结论和放射源负指数衰减的统计规律互相抵触.
然而,后者是描述处于统计平衡的量子系统(在时间
上“先先后后”被制备出的大量同一种不稳定粒子) ,
因而在dt 时间内的衰变数dN 必定正比于当时的粒
子数N ,并且可以认为这个比例系数(一般它应当与
该粒子已存活的时间无关, 但对长长短短的存活时
间作了统计平均后可以假定它为常数) 与t 无关,这
样一来对t 积分自然就得到负指数衰减的统计规
律;与此相对照, 前者是假定“在同一时刻”被制备
出的(大量同一种不稳定) 粒子的衰变规律, 每一时
刻粒子的衰变几率(也即这个比例系数) 一般和它
已经存活的时间有关. 由于两者研究的量子系统不
同,并不相互矛盾.
3. 2 量子Zeno 效应存在性的理论论证[2 ]
理论研究发现,频繁地对一个不稳定系统进行
量子测量将会抑制或阻止它的衰变(或跃迁) . 极端
而言,连续的量子测量将使不稳定系统稳定地保持
在它的初态上,完全不发生衰变或跃迁. 这种不稳定
初态的存活几率随测量频率增加而增加的现象就是
量子Zeno 效应[6 ] . 这个效应其实就是量子测量理论
的SchrÊdinger 方程的一个直接推论,是一个不存在
经典对应的纯量子现象. 应当强调指出,这里的量子
测量是完整意义上的量子测量,也即上一节所论述
的那一类可以分解为谱分解、随机坍缩和初态演化
三个阶段的量子测量.
设一个含时量子系统的初态为| ψ(0) > ,按照
Riemann - Lebesque 定理,随着这个不稳定系统的演
化, 其初态的存活几率P( t) =| < ψ(0) | ψ( t) >| 2
将越来越小. 当然,这个P( t) 按它的物理含义应当
只适用于自t = 0 开始演化之后,直到t 时刻才执行
检验初态存活与否的量子测量, 在(0 , t) 时间间隔
内不另进行任何这类量子测量. 现在问:如果在(0 ,
t) 之间再附加若干次这类量子测量, 到t 时刻初态
存活几率的实测值会不会发生变化?下面根据量子
测量理论所作的分析表明, 这时初态存活几率的实
测值应当增加. 具体如下:
将[0 , t ] 区间等分为N 份,在每一时刻tn =
nt
N
进行一次量子测量,以确认体系是否仍在| ψ(0) >
上. 按上面关于P( t) 含义的叙述,第一次在t
N
时刻
测量时,初态存活几率为P( t
N
) . 按测量理论, 除跃
190
云南民族学院学报(自然科学版) 第9 卷
迁或衰变掉的已经不予计入以外, 剩下的这P( t
N
)
部分将坍缩成为初态| ψ(0) 〉, 并以此时刻t
N
为初
始时刻再次重新开始演化,演化到2 t
N
时刻,再次作
类似测量,于是,经两次测量后到2 t
N
时刻, 总计的
初态存活几率成为[ P(
t
N
) ]2 . 如此继续推论下去,
最后可得:在[0 , t ] 内经受N 次等时间隔的测量后,
初态| ψ(0) > 的存活几率为
PN ( t) = [ P(
t
N
) ] N (3 - 4)
当N 足够大时t
N
足够小,可将P( t
N
) 展开并保留到
一阶项
P(
t
N
) ≈ 1 + P′(0)
t
N
如果令N → ∞,就过渡到在[0 , t ] 内为连续测量的
理想极限情况. 设这时存活几率为Pc ,有
Pc = lim
N →∞
(1 + P′(0) t
N
) N = eP′(0) t (3 - 5)
利用上面1 中的结论: P′(0) = 0 ,最后得到
Pc = 1 (3 - 6)
这就是说,一个不稳体系在经受连续量子测量时,会
一直处于它的初态而不发生(本应发生的) 衰变或
跃迁. 当然,尽管连续测量在原则上是存在的, 但实
验上常常不易实现, 因此应当给出有限次测量情况
下的结果. 为此,将上面P 的展开式近似到二阶项,
P( t
N
) ≈ 1 +
1
2 P″(0) t2
N2 注意P″(0) = - 2〈0 |
H(0) 2 | 0〉< 0 以及函数f ( x) = [1 -
c
x2 ] x ( c > 0)
在物理的条件下是单调上升的,即可得知:关于存活
几率与测量次数之间有如下不等式关系,
PN2 ( t) > PN1 ( t) , (当N2〉N1) (3 - 7)
于是,实验检验此效应是否存在只需做到:对于给定
的区间[0 , t ] ,用不同分次的实验来检验这个不等式
即可.
应当指出,以上关于量子测量及相关的讨论当
然是理想化的、概念性的. 尽管如此,上面叙述还是
足以令人相信:量子Zeno 效应揭示,在量子测量过
程中时间实际上是停滞了,就是说,量子测量导致时
间的塌缩[7 ] ! 这一深邃而难以捉摸的现象竟然直接
蕴含在量子理论的公设,特别是第三公设(测量公
设) 、第四公设(SchrÊdinger 方程公设) 这两个公设之
中,这是令人兴奋而又使人费解的.
4 量子态的超空间传送(量子Teleportation
及Swapping) ———空间均匀广延性的塌缩
4. 1 Quantum Teleportation 的六人方案[8 ]
1993 年Bennett 等六人开创性的提出了量子态
的Teleportation 这一概念,并设计了如下的单个两能
级量子态的teleportation 方案.
Alice 和Bob 两人分开不定的一段距离.
a. 现状是:Alice 有粒子1 和粒子2. 其中粒子
1 —处于信息态:
| <〉1 =α| 0〉1 +β| 1〉1 , (α,β) (4 - 1)
α、β是Alice 本人也不知道的任意两个未知的复系
数(满足归一条件) ———需要传送的信息. Bob 有粒
子2. 这里,粒子2 与粒子3 组成一个纠缠态———Bell
基中的|ψ- 〉23 ,它们构成Alice 和Bob 之间的一条量
子通道,
|ψ- 〉23 =
1
2
(| 0〉2| 1〉3 - | 1〉2| 0〉3)
于是,这三个粒子的总状态为
|ψ〉123 =
α
2
(| 0〉1 | 0〉2 | 1〉3 - | 0〉1| 1〉2 | 0〉3) +
β
2
(| 1〉1| 0〉2| 1〉3 - | 1〉1| 1〉2| 0〉3) (4 - 2)
现在的任务是: Alice 要将粒子1 的| <〉1 量子态(信
息态,实质是α、β两个系数) 传给Bob ,使他手中的粒
子3 的状态成为| <〉3α| 0〉3 +β| 1〉3 .
b. 开始动作是:Alice 对手中的粒子1 和2 作
关于Bell 基的联合测量,这相当于用下面的粒子1
和2 的完备基
|ψ±〉12 =
1
2
(| 0〉1| 1〉2 ±| 1〉1| 0〉2)
|ψ±〉12 =
1
2
(| 0〉1| 0〉2 ±| 1〉1| 1〉2)
对|ψ〉123作展开,可得|ψ〉123的展开式为
|ψ〉123 =
1
2
{|ψ- 〉12 ( - α| 0〉3 - β| 1〉3 ) + |ψ+〉12
( -α| 0〉3 +β| 1〉3) + | <- 〉12 (α| 1〉3 +β| 0〉3) + | <+〉12
(α| 1〉3 -β| 0〉3) }
并产生态的塌缩. 这些随机塌缩(投影) 的结果有四
种,它们的几率相等.
c. 接下来,Alice 用经典办法广播测量结果.
d. Bob 根据Alice 的广播,来选择对手中粒子
3 所作的幺正变换,最终实现未知量子态的转移: |
<〉1 →| <〉3 . 这四种情况是:
第一种情况,若Alice 宣布她得到|ψ- 〉12 (即|
191
第4 期张永德: 量子测量与时空塌缩
ψ〉123
坍缩到
展式的第一项) ,与此相应,Bob 手上粒
子3 的态必定关联坍缩为(α| 0〉3 +β| 1〉3) . 这时Bob
无须作任何操作即可获得(Alice 手上粒子1 原先所
处的) 信息态.
第二种情况,若Alice 宣布测得|ψ+ 〉12 (即|ψ〉123
坍缩到
展式的第二项) ,则粒子3 的态必定关联坍
缩为( -α| 0〉3 +β| 1〉3) . 这时Bob 只要对手中的粒子
3 施以σz 变换,
σz ( -α| 0〉3 +β| 1〉3) =
1 0
0 - 1
β
-α 3
=
α| 0〉3 +β| 1〉3 ,
他就可以获得Alice 手中的信息态.
第三种情况,若Alice 宣布测得|ψ- 〉12 (即|ψ〉123
坍缩到
展式的第三项) ,则粒子3 的态必为(α| 1〉3 +
β| 0〉3) . 这时Bob 对粒子3 施以σz 变换,
σx (α| 1〉3 +β| 0〉3 ) =
0 1
1 0
α
β 3
=α| 0〉3 +
β| 1〉3
Bob 就能得到信息态.
第四种情况,Alice 宣布测得|ψ+ 〉12 (即| ψ〉123
坍缩到
展式的第四项) ,粒子3 的态必为(α| 1〉3 -
β| 0〉3) . 这时Bob 对粒子3 施以σy 变换
σy (α| 1〉3 -β| 0〉3) =
0 - i
i 0
α
-β 3
=
i (α| 0〉3 +β| 1〉3)
即可获得信息态.
4. 2 Quantum Teleportation 的几点注记:
a. 过程不违背非克隆定理[9 ] . Alice 手上的
粒子1 在测量后已不处于原来状态. 过程只是原来
信息态的转移(1 # →3 # ) ,不是信息态的复制.
b. 不存在信息的瞬时传递 Bob 必须等候收
听Alice 测量的结果. 所以不违背狭义相对论原理.
这一过程中信息分为两部分:量子信息(瞬时的超空
间的传递,见下) 和经典信息( ≤光速) . 最终信息传
递速度≤光速. 注意,Bob 在收听之前,甚至不知道
Alice 做了测量与否,更谈不上知道Alice 的测量结
果(或自己手中粒子的状态) 如何.
c. 借助交缠态传送量子信息,这是量子交缠
的重要实际应用之一.
d. 贝尔基测量: Hadamard 门加C - NOT 操
作. 目前只能实验证认两个Bell 基. 此实验首次于
1997 年由Bowmeester 、潘建伟和Zeilinger 等人所实
现[10 ] .
e. 这个Teleportation 方案可以从理论上推广.
对于n 个粒子每个粒子有s 个能级的普遍情况,以
及受控的Teleportation 方案均已拟出[11 ] .
4. 3 量子纠缠交换(Entanglement Swapping) 实验
量子纠缠是量子理论中又一个具有基本特征性
的实验现象. 从前以为,只有通过相互作用才能产生
它. 现在,这个实验表明,它既可以在无直接相互作
用的情况下以间接方式产生,又可以通过超空间方
式来制造和传递.
众所周知,在给定一组基矢之后,任一量子态的
基本特征是展开式中各项系数以及各项间的纠缠方
式这两点(后者还依赖于前者) . 因此,任一量子态的
超空间传送也就归结为这两种内容的传送. 关于这
一点,最简单的原型是量子Teleportation 实验;关于
第二点,最简单的原型便是Sweapping 实验.
由于量子纠缠的形式有无限多种,所以量子纠
缠的超空间传送也就有无限多种. 最简单的一种就
是现在常说的entanglement swapping. 这个方案的原
理很简单,如下:
Alice 是发送者,她与两个可能相距很远(并且
可能也不知道他们在何处) 的接收者Bob 和Charlie
分别共享两对EPR 粒子(1 和2) 和(3 和4) . 其中粒
子1 为Bob 所有,粒子2 和3 为Alice 所有,粒子4 为
Charlie 所有. 于是构成了Alice - Bob 和Alice - Char2
lie 两个量子通道. 由于态|ψ- 〉便于实验辩认(见下
面叙述) ,选取两个EPR 对均为态|ψ- 〉. 于是系统的
初始态矢为
|ψ〉1234 = |ψ- 〉12|ψ- 〉34 =
1
2
(| 0〉1| 1〉2 -
| 1〉1| 0〉2) (| 0〉3| 1〉4 - | 1〉3| 0〉4) (4 - 4)
对于光子情况,这里的| 0〉和| 1〉分别表示极化方向
为垂直| V〉和水平| H〉的态. 此时Alice 对手中粒子2
和3 执行Bell 基的联合测量. 这相当于将(4 - 4) 式
按粒子2 和3 的Bell 基|ψ±〉23和| <±〉23展开
|ψ〉1234 =
1
2
{ψ+〉14|ψ+〉23 - |ψ- 〉14|ψ- 〉23 -
| <+〉14| <+〉23 + | <- 〉14| <- 〉23}
并且向四项中的任一项作等几率的随机塌缩(投
影) . 如果粒子2 和3 的状态塌缩向| <+〉23 ,粒子1
和4 便塌缩向| <+〉14 ;如果粒子2 和3 的状态塌缩
向|ψ- 〉23 ,粒子1 和4 便塌缩向|ψ- 〉14 ,等等. 总之,
由粒子2 和3 的纠缠状态便可以知道粒子1 和4 的
纠缠状态. 这说明,尽管粒子1 和4 离开粒子2 和3
很远,并且可能彼此相距也很远,而且也从未发生过
192
云南民族学院学报(自然科学版) 第9 卷
直接的相互作用,却能彼此纠缠起来. 这种做法等于
摇控制造已知的量子纠缠,或者更确切说,是量子纠
缠的超空间传送,也即量子纠缠交换(entanglement
swapping) .
1998 年,量子交缠的超空间传送实验也首次由
潘建伟等人所完成[12~13 ] . 实验中证认的是|ψ- 〉23和
|ψ- 〉14 . 这是因为,在四个Bell 基{|ψ±〉,| <±〉}中,
目前实验只能辩认它们四个中的|ψ- 〉(和|ψ+ 〉}. 关
于Bell 态|ψ- 〉的控测原理是这样的:|ψ- 〉是四个基
中唯一一个极化状态为反对称的基,其余均为对称
的. 由于光子是玻色子,双光子态的总波函数必定是
对称的,既然总自旋态是反对称的,总的空间波函数
就必定也是反对称的. 当两个入射光子入射到分束
器(beam splitter) 时,出射的两个光子必定分开出现
在分束器的两个不同的出射端. 于是,在分束器后的
不同出射端放置两个探测器并计录它们的符合计
数,这样的实验安排就等于只探测四个Bell 中的|
ψ- 〉. 在此基础上, 按理整个实验是对| ψ- 〉23 和|
ψ- 〉14态中的两对光子进行四重符合计数. 但由于他
们的实验是着重说明:在对光子2 和3 做了|ψ- 〉的
测量安排并得到计数之后,光子1 和4 将处在量子
纠缠态|ψ- 〉中并且极化相互正交,所以采用让光子
1 再通过一个极化分束器以形成D+
1 (45。极化) 和
D-
1 ( - 45。极化) 两个输出,接着测量在D4 (极化方
向θ可变) 和D+
1 以及D4 和D-
1 之间的两个双重即
四重符合计数曲线(符合计数率———θ) . 实验用的光
子源是:钛- 蓝宝石激光器产生的激光,在非线性
LBO(LiB3O5) 中被倍频以得到紫外UV 脉冲. 然后此
UV 脉冲借助反射先后两次穿过一块BBO(βBaB2O4)
晶体,分别产生全都处于|ψ- 〉态的两个光子关联对
2 - 3 和1 - 4.D+
1 - D4 和D-
1 - D4 对θ的实验符合曲
线清楚显示光子1 和4 已处于Bell 态|ψ- 〉14上.
由于这个实验的成功,到此可以认为,量子态的
超空间传送已经完全实现.
5 量子Zeno 效应
一方面,鉴于在任何物理理论中,特别是在任何
量子理论中,时间都是连续变化的参量,因此以前总
认为:在同一个Lorents 参考系中看来,任何相互作
用都不会影响时间的均匀流淌的性质. 换句话说,时
间是任何相互作用所不能动摇的. 但现在, 量子
Zeno 效应表明:测量中,系统的时间竟然不流淌了,
时间停滞了,或者说,时间塌缩了. 另一方面,量子
Teleportation 实验和进一步的Swapping 实验表明:
(不是信息传送过程,而是) 系数α、β以及各类量子
交缠的传送总是瞬时的. 更准确地说,塌缩使量子态
从甲到乙的传送具有以下三个奇异特征:i . 瞬时的;
ii . 不必事先知道乙在何处;iii . 也决不会为甲乙之间
传送途中任何障碍所阻隔. 依据这三个奇异特征,我
们完全有理由说,在量子态塌缩时,空间的广延性被
塌缩了. 简单地说,空间塌缩了.
将这两方面结合起来,可以总结为:量子测量所
造成的塌缩,不仅(本质上就是) 随机的、不可逆的、
斩断相干性的,而且是非定域的,具有超时空的性
质. 一句话,量子测量既可以使时间的均匀流淌性消
失,又可以使空间的均匀广延性消失! 如此奇妙的
物质结论竟然早就蕴含在量子力学的前提公设中,
这确实是让人费解而又令人兴奋的.
当然,如前面所说,上面对量子测量及塌缩的分
析是理想化和简单化的. 尽管如此,这里所作的分析
和所得的结论,就基本概念而言无疑是正确的. 特别
是,这些奇妙结论已经逐步对近几年来的实验所证
实. 按照目前量子理论发展的形势可知,从实验和理
论两个方面开展对量子测量和塌缩现象的直接研究
是一个基础性的、十分重要的大课题. 这方面的任何
进展都将从根本上改变和丰富我们对所处时空的认
识.
参考文献
1. P.A.M. 狄拉克量子力学原理[M] ,科学出版社,1965
第4章基因表达.doc 全文文档投稿网 - max上传文档投稿赚钱
max.book118.com › 海量文档 › 临时分类 - 轉為繁體網頁
《生命是什么》(英语:What Is Life?)是物理学家薛定谔的一本生物学著作,發表於1944年。著作完成的时候生物的遺傳物質結構尚未被發現,但是薛丁格在该書中講述許多關於遺傳分子的理論性推測。許多早期的分子生物學家皆曾表示自己受這本書的影響。
而你的精神的火热般想象的飞腾默从了一个映象,一个比喻。——歌德
32. 古典物理学无法解释的不变性
借助于X射线的精密仪器(物理学家会记得,这种仪器在三十年前揭示了晶体的详细的原子晶格结构),在生物学家和物理学家的共同努力下,最近已成功地把负责个体的某一宏观特性的显微结构的体积--“基因的体积”--的上限降低了,并且降低到远远低于第19节得出的估计数。我们现在严肃地面临着的问题是:从统计物理学的观点来看,基因结构似乎只包含了很少量的原子(一般是一千个,也可能还要少)可是它却以奇迹般的不变性表现了最有规律的活动,我们如何使这两方面的事实协调起来呢?
让我再一次把这种确实令人惊奇的情况说得形象化些。哈布斯堡王朝的一些成员有一种特别难看的下唇(哈布斯堡唇)。在王室的赞助下,维也纳皇家学院仔细地研究了它的遗传,并连同完整的历史肖像一并发表了。已证明这种特征是正常唇形的一个真正的孟德尔式的“等位基因”。如果我们注意到十六世纪时该家族中一个成员的肖像,和他的生活在十九世纪的后代的肖像,我们完全可以肯定,决定这种畸形特征的物质性的基因结构,已经世代相传经历了几个世纪,每一代之间细胞分裂的次数不是很多的,可是每一次细胞分裂都忠实地复制了。此外,这个基因结构所包含的原子数目很可能同X射线试验测得的原子数目是同一个数量级。在所有时间里,基因保持华氏98度左右的温度。它能够不受热运动的无序趋向的干扰保持了几个世纪,这一点我们又如何理解呢?
上世纪末的一位物理学家,如果他只打算根据他所能解释的、他真正理解的那些自然界的定律去解释这个问题,他将是一筹莫展的。在对统计学的情况稍加考虑以后,他也许会作出回答(如我们将看到的是正确的回答):这些物质结构只能是分子。关于这些原子的集合体的存在,它有时是高度温定的,对此,当时的化学已有了广泛的了解。不过这种了解是纯粹经验的。对分子的性质还不了解——使分子保持一定形状的、原子间强有力的作用键,对每个人来说,完全是个谜。事实上,这个问答证明是正确的,可是,它只是把这种莫名其妙的生物学稳定性追溯到同样莫名其妙的化学稳定性,所以是无济于事的。根据同一个原理去证明两种特性在表明上是相似的,只要这个原理本身还是未知的那个证明就永远是靠不住的。
33. 可以用量子论来解释
在这种情况下,量子论弥补了不足之处。根据现在的了解,遗传的机制是同量子论的基础密切相关的,不,是建立在量子论的基础之上的。量子理论是马克斯?普朗克于1900年发现的。现代遗传学可以从德弗里斯、科伦斯和切尔玛克(1900年)重新发现孟德尔的论文,以及从德弗里斯关于突变的论文(1901—1903年)那时算起。因此,这两大理论几乎是同时诞生的,而且它们两者一定要在相当成熟后才会发生联系,这也是不足为奇的。在量子论方面,化了四分之一世纪多的时间,直到1926—1927年W.海特勒和F.伦敦才制定出化学键的量子论的一般原理。海特勒—伦敦理论包含了量子论最新进展的最精细而错综复杂的概念(叫做“量子力学”或“波动力学”)。不用微积分的描述几乎是不可能的,否则至少要写象本书一样的另一本小册子。不过,好在是全部工作现在都已完成了,并有助于澄清我们的思想,看来有可能以更直截了当的方式指出“量子跃迁”同突变之间的联系,立即搞清楚最主要的项目。我们在这里就是试图做到这一点。
34. 量子论——不连续状态——量子跃迁
量子论的最大启示是在“自然界的圣典”里发现了不连续性的特点,而当时的观点却认为自然界中除了连续性外全都是荒谬的。
第一个这样的例子涉及到的是能量。一个物体在很大范围内连续地改变着它的能量。例如一个摆,它的摆动由于空气的阻力逐渐缓慢下来。十分奇怪的是,它却证明了,必须承认在原子这一级上的系统的行为是不同的。根据我们不能在这里详细说明的那些理由,我们必须假定一个小的系统由于它自己的性质,只能具有某种不连续的能量,称为它的特殊的能级。从一种状态转变为另一种状态,是一种相当神秘的事情,通常称之为“量子跃迁”。
不过能量并不是一个系统的唯一的特征。再以我们的摆为例但是把它想象成能够作出各种运动的摆,如天花板上悬下一根绳子,挂上一个重球,它能够作南北向、东西向或任何其他方向上的摆动,或者作圆形或椭圆形的摆动。用一只风箱轻轻地吹这只球,便能是它从运动的一种状态连续地转变到任何另一种状态。
对于微观系统来说,这些特征或相似的特征——对此我们不能详细地讨论了——的大多数都是不连续地发生变化的。它们是“量子化”的,能量恰恰就是如此。
结果是许多个原子核,包括它们的电子卫兵,当发现它们自己(彼此)靠拢形成“一个系统”时,原子核是无法通过自己的性质来选择一种我们所能想象到的任何适宜的构型的。它们的性质使它们可以选择的只是大量的、但是不连续的“状态”系列。我们通常称它们为级或能级,因为能量是这种特征的十分重要的部分。但是必须懂得,对它的完整的描述,要包括能量以外的更多的东西。认为一种状态是意味着全部微粒的一种确定的构型,这种想法实际上是正确的。
一种构型转变为另一种构型就是量子跃迁。如果第二种构型具有更大的能量(“是较高的能级”),那么,外界至少要供给这个系统以两个能级间的能量差额,才能使转变成为可能。它也可以自发地变到较低的能级,通过辐射来消耗多余的能量。
35. 分子
在原子选定的一组不连续状态中间,不一定是、但可以是使核彼此紧密靠拢的最低能级。在这种状态中,原子组成了分子。这里有一点是要着重指出的,即分子必须具有一定的稳定性;除非外界供给它以“提高”到邻近的较高能级所需的能量差额,否则,构型是不会改变的。因此,这种数量十分确定的能级差是定量地决定了分子的稳定程度。我们将会观察到,这个事实同量子论的基础本身,也就是同能级图式的不连续性的联系是多么的密切。
我必须请读者姑且认为这些观点的体系已经被化学事实彻底地核实过了;而且它已经证明在解释化学原子价的基本事实和关于分子结构的许多细节,如它们的结合能,它们在不同温度下的稳定性等方面是成功的。我是无法详细地加以检验的。
36. 分子的稳定性有赖于温度
我们必须因考察了生物学问题中最有兴趣的一点,即不同温度下的分子稳定性而感到满足。假定我们的原子系统一开始确实是处在它的最低能级的状态。物理学家称之为绝对零度下的分子。要把它提高到相邻的较高的状态或能级,就需要供给一定的能量。最简单的供给能量的方式是给分子“加热”。把它带进一个高温环境(“热浴”),让别的系统(原子,分子)冲击它。考虑到热运动的完全不规则性,所以不存在一个可以肯定的、并立即引起“提高”的、截然分明的温度界限。更确切地说,在任何温度下(只要不是绝对零度),都有出现“提高”的机会,这种机会是有大有小的,而且当然是随着“热浴”的温度而增加的。表达这种机会的最好的方式是,指出在发生“提高”以前你必须等待的平均时间,即“期待时间”。
根据M.波拉尼和E.维格纳的研究,“期待时间”主要取决于二种能量之比,一种能量正好就是为了“提高”而需要的能量差额本身(我们用W来表示),另一种能量是描述在有关的温度下热运动强度的特性(我们用T表示绝对温度,kT表示特有的能量)。有理由认为,实现“提高”的机会愈小,期待时间便愈长,而“提高”本身同平均热能相比也就愈高,就是说,W:kT之比值的相当小的变化,会大大地影响期待时间。例如(按照德尔勃留克的例子),W是kT的三十倍,期待时间可能只短到1/10秒;但当W是kT的五十倍时,期待时间将延长到十六个月;而当W是kT的六十倍时,期待时间将延长到三万年!
对于那些对数学感兴趣的读者来说,可以用数学的语言来说明这种对于能级或温度变化高度敏感的理由,同时再加上一些类似的物理学的说明。其理由是,期待时间(称之为t)是通过指数函数的关系依赖于W/kT之比的;于是
t=cEXP(W/kT)
c是10的-13或-14次方秒这么小的数量级的常数。这个特定的指数函数并不是一种偶然的特性。它一再出现在热的统计学理论中,似乎构成了该理论的基本内容。它是在系统的某个部分中,偶然地聚集象W那么大的能量的不可能性的几率的一种度量。当需要有好几倍的“平均能量”kT时,增加得如此巨大的就是这种不可能性的几率。
实际上,W=30kT(见上面引用的例子)已经是极少有的了。当然,它之所以还没有导致很长的期待时间(在我们的例子中只有1/10秒),是由于c因子是很小的缘故。这个因子具有物理学的意义。它是整个时间内,在系统里发生的振动周期的数量级。你可以非常概括地描述这个因子,认为它是积聚起所需要的W总数的机会,它虽然很小,可是在“每一次振动”里是一再出现的,就是说,每秒大约有10的13或14次方次。
38. 第一个修正
提出这些理由作为分子稳定性理论时,就已经是默认了我们称之为“提高”的量子跃迁如果不是导致完全的分解,至少也是导致相同的原子构成了本质上不同的构型——一种同分异构分子,正如化学家说的,那是由相同的一些原子按不同的排列所组成的分子(应用到生物学上时,它就代表同一个“位点”上的不同的“等位基因”,量子跃迁则代表突变)。
对这个解释,必须作两点修正,为了使人们易于了解,我有意把它说得简单化些。根据我所讲的,可能会认为只有在极低的能量状态下,一群原子才会组成我们所说的分子,而下一个比较高的状态已经是“别的一些东西”了。并不是这样的。事实上,即使在最低能级的后面,还有着一系列密集的能级,这些能级并不涉及到整个构型的任何可以察觉的变化,而只是对应于原子中间的那些微小的振动,这种振动我们在第37节里已经讲了。它们也都是“量子化”的,不过是以较小的不子从一个能级跳到相邻的能级。因此,在低温下,“热浴”粒子的碰撞已足以造成振动。如果分子是一种伸展的结构,你可以把这些振动想象为穿过分子而不发生任何伤害的高频声波。
所以,第一个修正并不是十分重大的:我们可以不去理会能级图式的“振动的精细结构”。“相邻的较高能级”这个术语可以这样来理解,即与构型的改变相对应的相邻的能级。
39. 第二个修正
第二个修正解释起来更加困难,因为它关系到各种能级图式的某种重要而又复杂的特性。两个能级之间的自由通道也许被阻塞了,更谈不上供给所需要的能量了;事实上,甚至从比较高的状态到比较低的状态的通路也可能阻塞了。
让我们从经验事实谈起吧。化学家都知道,相同的原子团结合组成分子的方式不止一种。这种分子叫做同分异构体(“由同样的成分组成的”)。同分异构现象不是一种例外,而是一种规律。分子愈大,提供的同分异构体也就愈多。一种最简单的情况,即同样由三个碳原子八个氢原子和一个氧原子所组成的两种丙醇。氢和碳之间氧都能够插入,但只有两种情况才是不同的物质。它们确实也是如此。它们所有的物理常数和化学常数都是明显不同的。它们的能量也不同,代表了“不同的能级”。
值得注意的是两个分子都是完全稳定的,它们的行为就象它们都是处于“最低状态”。不存在从一种状态到另一种状态的自发转变。
理由是两种构型并不是相邻的构型。要从一种构型转变为另一种构型,只能通过介乎两者之间的中间构型才能发生,这种中间构型的能量比它们当中的任何一种构型都要高。粗浅地说,氧必须从一个位置抽出来,插到另一个位置上。如果不经过能量相当高的构型,看来是无法完成这种转变的。
现在可以提出我们的“第二修正”了,即这一类“同分异构体”的变化,是在生物学应用中我们唯一感到兴趣的一种变化。这些变化就是我们在第35节到37节中解释“稳定性”时所必须牢记的。我们所说的“量子跃迁”,就是从一种相对稳定的分子构型变到另一种构型。供给转变所需的能量(其数量用W表示)并不是真正的能级差,而是从初级能量上升到阈的步阶。
在初态和终态之间不介入阈能的转变是毫无意义的,这不仅在生物学应用上是如此。这种转变对分子的化学稳定性确实是毫无作用的,为什么呢?因为它们没有持久的效应,它们是不引人注意的。由于没有什么东西阻止它们的回路,所以当它们发生转变时,几乎就立刻回复到初态了。
确实的,正如光明显出了它自身,也显出了黑暗一样,于是,真理是它自身的标准,也是谬误的标准。
——斯宾诺莎《伦理学》第二部分,命题43
40. 遗传物质的一般图景
根据这些事实,可以很简单地回答我们的问题,就是说:由少量原子组成的这些结构,能否长时间地经受住象遗传物质不断受到的那种热运动的干扰影响?我们将假定一个基因的结构是一个巨大的分子,只能发生不连续的变化,这种变化是在于原子的重新排列并导致一种同分异构的分子。这种重新排列也许只影响到基因中的一小部分区域,大量的各种不同的重新排列也许是可能的。从任何可能的同分异构体中,把实际的构型分离出来的阈能一定是很高的(这是同一个原子的平均热能相比),以致使这种变化成为一种罕有事件。这种罕有事件我们认为就是自发突变。
本章的以后几部分将致力于检验基因和突变的一般描述(主要应归功于德国物理学家M.德尔勃留克),把它同遗传学事实作详细的比较。在此之前,我们可以对这一理论的基础和一般性质适当地作些评论。
41. 图景的独特性
为生物学问题去穷根究底,并把图景建立在量子力学的基础之上,这是绝对必要的吗?基因是一个分子,这样的猜测,我敢说,在今天已是老生常谈了。不管他是不是熟悉量子论,不同意这种猜测的生物学家是很少的了。在第32节中,我们大胆地适用了量子论问世以前的物理学家的语言,作为观察到的不变性的唯一合理的解释。随后是关于同分异构性,阈能,W:kT在决定同分异构体变化几率中的重要作用等因素的理由——所有这一切理由,都可以在纯粹经验的基础上很好地加以说明;不管怎样,反正都不是来源于量子论的。既然在这本小册子里,我不能真正地把它讲清楚,而且还可能使许多读者感到厌烦,那我为什么还要如此强烈地坚持量子力学的观点呢?
量子力学是根据一些最好的原理来说明自然界中实际碰到的、原子的各种集合体的第一个理论方法。海特勒-伦敦键是这个理论的一个独特的特点,但是这个理论并不是为了解释化学键而发明的。它是以一种十分有趣而且费解的方式出现的,是根据完全不同的理由强加给我们的。现已证明,这个理论同观察到的化学事实是十分吻合的,而且,正如我所说的,这是一个独特的特点,由于对这个特点有足够的了解,所以可以相当肯定地说,在量子论的进一步发展中,“不可能再发生这样的事情了”。
因此,我们可以满有把握地断言,除了遗传物质的分子解释外,不再有别的解释了。在物理学方面不再有别的可能性可以解释遗传物质的不变性。如果德尔勃留克的描述是不管用的,那么,我们将不得不放弃作进一步的尝试。这是我想说明的第一点。
42. 一些传统的错误概念
但是,也许可以问:除了分子以外,难道真的就没有由原子构成的、其他的可以持久的结构了吗?比如,埋在坟墓里一、二千年的一枚金币,难道不是保留着印在它上面的人像的模样吗?这枚金币确实是由大量原子构成的,但在这个例子中,我们肯定不会把这种形象的保存归因于巨大数字的统计。这种说法同样也适用于我们发现蕴藏在岩石里的、经过几个地质时代而没有发生变化的一批明莹的晶体。
这就引出了我要说明的第二点。一个分子,一个固体,一块晶体的情况并没有真正的差别。从现代的知识来看,它们实质上是相同的。不幸的是,学校的教学中还保持着好多年前就已过时了的传统观念,从而模糊了对实际事态的了解。
其实,我们在学校里学到的有关分子的知识,并没有讲到分子对固态的相似程度比对液体或气态更为接近的观点。相反,教给我们的是要仔细地区分物理变化和化学变化;物理变化如熔化或蒸发,在这种变化中,分子是保持着的(比如酒精,不管它是固体、液体还是气体,总是由相同的分子C2H6O组成的)。化学变化如酒精的燃烧,在那里,一个酒精分子同三个氧分子经过重新排列生成了二个二氧化碳分子和三个水分子。
关于晶体,我们学到的是它们形成了周期性的三向堆叠的晶格,晶格里的单个分子的结构有时是可以识别的,酒精和许多有机化合物就是如此;在其他的晶体中,比如岩盐(氯化钠,NaCl),氯化钠分子是无法明确地区分界限的,因为每个钠原子被六个氯原子对称地包围着,反过来也是如此;所以说,如果有钠氯原子对的话,那么,不管哪一对都可以看作是氯化钠分子的组成。
最后,我们还学到,一个固体可以是晶体,也可以不是晶体,后一种情况,我们称之为无定形的固体。
43. 物质的不同的“态”
目前,我还没有走得那么远,想把所有这些说法和区别都说成是错误的。它们在实际应用中往往是有用的。但在物质结构的真实性方面,必须用完全不同的方法划清一些界限。基本的区别在下面的“等式”的等号之间:
分子=固体=晶体
气体=液体=无定形的固体
对这些说法,我们必须作简要的说明。所谓无定形的固体,要么不是真正的无定形,要么不是真正的固体。在“无定形的”木炭纤维里,X射线已经揭示出石墨晶体的基本结构。所以,木炭是固体,但也是晶体。在我们还没有发现晶体结构的地方,我们必须把它看作是“粘性”(内摩擦)极大的一种液体。这样一种没有确定熔化温度和熔化潜热的物质,表明它不是一种真正的固体。将它加热时,它逐渐地软化,最后液化而不存在不连续性(我记得在第一次世界大战末期,在维也纳曾经有人给我们象沥青那样的东西作为咖啡的代用品。它是这么硬,必须在它出现光滑的贝壳似的裂口时,用凿子或斧头把它砸成碎片。可是,过一段时间后,它会变成液体,如果你很蠢地把它搁上几天,它就会牢牢地粘在容器的底部)。
气态和液体的连续性是非常熟悉的事情。可以用“围绕”所谓临界点的方法,使任何一种气体液化,也就没有什么不连续性。但这个问题我们在这里不准备多谈了。
44. 真正重要的区别
这样,上述图式中除了主要之点外,我们都已证明是有道理的;这个主要之点就是我们想把一个分子看成是一种固体=晶体。
这一点的理由是,把一些原子,不管它有多少,结合起来组成分子的力的性质,同把大量原子结合起来组成真正的固体——晶体的力的性质是一样的。分子表现出同晶体一样的结构稳固性。要记住,我们正是从这种稳固性来说明基因的不变性的!
物质结构中真正重要的区别在于原子是不是被那种“起稳固作用的”海特勒-伦敦力结合在一起。在固体中和在分子中,原子是这样结合的。在单原子的气体中(比如水银蒸气),它们就不是那样了。在分子组成的气体中,只是在每个分子中,原子才是以这种方式结合在一起的。
45. 非周期性的固体
一个很小的分子也许可以称为“固体的胚”。从这样一个小的固体胚开始,看来可以有两种不同的方式来建造愈来愈大的集合体。一种是在三个方向上一再重复同一种结构的、比较乏味的方式。这是一个正在生长中的晶体所遵循的方式。周期性一旦建立后,集合体的大小就没有一定的限度了。另一种方式不用那种乏味的重复的图样,而是建造愈来愈扩大的集合体。那就是愈来愈复杂的有机分子,这种分子里的每一个原子,以及每一群原子都起着各自的作用,跟其他的原子起的作用(比如在周期性结构里的原子)是不完全相同的。我们可以恰当地称之为一种非周期性的晶体或固体,并且可以用这样的说法来表达我们的假说:我们认为,一个基因——也许是整个染色体纤丝——是一种非周期性的固体。
46. 压缩在微型密码里的内容的多样性
经常会碰到这样的问题:象受精卵细胞核这样小的物质微粒,这么能包含了涉及有机体未来的全部发育的精细的密码正本呢?一种赋予足够的抗力来永久地维持其秩序的、秩序井然的原子结合体,看来是一种唯一可以想象的物质结构,这种物质结构提供了各种可能的(“异构的”)排列,在它的一个很小的空间范围内足以体现出一个复杂的“决定”系统。真的,在这种结构里,不必有大量的原子就可产生出几乎是无限的可能的排列。为了把问题讲清楚,就想到了莫尔斯密码。这个密码用点(“?”)、划(“-”)两种符号,如果如果每一个组合用的符号不超过四个,就可以编成三十种不同的代号。现在如果你在点划之外再加上第三种符号,每一个组合用的符号不超过十个,你就可以编出88572个不同的“字母”;如果用五种符号,每一个组合用的符号增加到25个,那编出的字母可以有37529846191405个。
可能有人会不同意,他们认为这个比喻是有缺点的,因为莫尔斯符号可以有各种不同的组合(比如,?--和??-)因此与同分异构体作类比是不恰当的。为了弥补这个缺点,让我们从第三种情况中,只挑出25个符号的组合,而且只挑出由五种不同的符号、每种符号都是五个所组成的那种组合(就是由五个点,五个短划……等组成的组合)。粗粗地算一下,组合数是62330000000000个,右边的几个零代表什么数字,我不想化气力去算它了。
当然,实际情况决不是原子团的“每一种”排列都代表一种可能的分子;而且,这也不是任意采用什么样的密码的问题,因为密码正本本身必定是引起发育的操纵因子。可是,另一方面,上述例子中选用的数目(25个)还是很少的,而且我们也只不过设想了在一条直线上的简单排列。我们希望说明的只不过是,就基因分子的图式来说,微型密码是丝毫不错地对应于一个高度复杂的特定的发育计划,并且包含了使密码发生作用的手段,这一点已经不再是难以想象的了。
47. 与事实作比较:稳定性的程度;突变的不连续性
最后,让我们用生物学的事实同理论的描述作比较。第一个问题显然是理论描述能否真正说明我们观察到的高度不变性。所需要的阈值数量--平均热能kT的好多倍--是合理的吗?是在普通化学所了解的范围之内吗?这些问题是很寻常的,不用查表据可肯定地回答。化学家能在某一温度下分离出来的任何一种物质的分子,在那个温度下至少有几分钟的寿命(这是说得少一点,一般说来,它们的寿命要长得多)。这样,化学家碰到的阈值,必定正好就是解释生物学家可能碰到的那种不变性所需要的数量级;因为根据第36节的描述,我们会记得在大约1:2的范围内变动的阈值,可以说明从几分之一秒到几万年范围内的寿命。
为了今后的参考,我提一些数字。第36节的例子里提到的W/kT之比,是:W/kT=30,50,60,分别产生的寿命是1/10秒,16个月,30000年。在室温下,对应的阈值是0.9,1.5,1.8电子伏。必须解释一下“电子伏”这个单位,这对物理学家来说是很方便的,因为它是可以具体化的。比如,第三个数字(1.8)就是值被2伏左右的电压所加速的一个电子,将获得正好是足够的能量去通过碰撞而引起转变(为了便于作比较,一个普通的袖珍手电筒的电池有3伏)。
根据这些理由可以想象到,由振动能的偶然涨落所产生的、分子某个部分中的构型的一种异构变化,实际上是十足的罕有事件,这可以解释为一次自发突变。因此,我们根据量子力学的这些原理,解释了关于突变的最惊人的事实,正是由于这个事实,突变才第一次引起了德弗里斯的注意,就是说,突变是不出现中间形式的,而是“跃迁式”的变异。
48. 自然选择的基因的稳定性
在发现了任何一种电离射线都会增加自然突变率以后,人们也许会认为自然率起因于土壤和空气中的放射性,以及宇宙射线。可是,与X射线的结果作定量的比较,却表明“天然辐射”太弱了,只能说明自然率的一小部分。
倘若我们用热运动的偶然的涨落来解释罕有的自然突变,那么,我们就不会感到太惊奇了,因为自然界已成功地对阈值作出了巧妙的选择,这种选择必然使突变成为罕见的。因为频繁的突变对进化是有害的,这是在前几节中已经得出的结论。一些通过突变得到不很稳定的基因构型的个体,它们那些“过分频繁的”、迅速地在发生突变的后代能长期生存下去的机会是很小的。物种将会抛弃这些个体,并将通过自然选择把稳定的基因集中起来。
49. 突变体的稳定性有时是较低的
至于在我们的繁育试验中出现的、被我们选来作为突变体以研究其后代的那些突变体,当然不能指望它们都表现出很高的稳定性。因为它们还没有经受过“考验”--或者,如果说是已经受过“考验”了,它们却在野外繁殖时被“抛弃”了--可能是由于突变可能性太高的缘故。总而言之,当我们知道有些突变体的突变可能性比正常的“野生”基因要高得多的时候,我们是一点也不感到奇怪的。
50. 温度对不稳定基因的影响小于对稳定基因的影响
这一点使我们能够检验我们的突变可能性的公式:t=cEXP(W/kT)(我们还记得,t是对于具有阈能W的突变的期待时间。)我们问:t是如何随温度而变化的?从上面的公式中,我们很容易找到温度为T+10时的t值同温度为T时的t值之比的近似值=EXP(-10W/kT)。
指数是负数,比率当然小于1。温度上升则期待时间减少,突变可能性就增加。现在可以检验了,而且已经在果蝇受得了的温度范围内,用果蝇作了检验。乍看起来,这个结果是出乎意料的。野生基因的低的突变可能性明显地提高了,可是一些已经突变了的基因的较高的突变可能性却并未增加,或者说,增加很少。这种情况恰恰是我们在比较两个公式时预期到的。根据第一个公式,要想使t增大(稳定的基因)就要求W/kT的值增大;而根据第二个公式,W/kT的值增大了,就会使算出来的比值减小,就是说,突变可能性将随着温度而有相当的提高。(实际的比值大约在1/2到1/5之间。其倒数2-5是普通化学反应中所说的范霍夫因子。)
51. X射线是如何产生突变的
现在转到X射线引起的突变率,根据繁育试验我们已经推论出,第一(根据突变率和剂量的比例),一些单一事件引起了突变;第二(根据定量的结果,以及突变率取决于累积的电离密度而同波长无关的事实),为了产生一个特定的突变,这种单一事件必定是一个电离作用,或类似的过程,它又必须发生在只有大约边长10个厘米距离的立方体之内。根据我们的描述,克服阈值的能量一定是由爆炸似的过程,如电离或激发过程所供给的。我所以称它为爆炸似的过程,是因为一个电离作用花费的能量(顺便说一下,并不是X射线本身花费的,而是它产生的次级电子所耗用掉的),有30个电子伏,大家很清楚,这是相当大的。这样,在放电点周围的热运动必定是大大地增加了,并且以原子强烈振动的“热波”形式从那里散发出来。这种热波仍能供给大约10个原子距离的平均“作用范围”内所需的一、二个电子伏的阈能,这也不是不可想象的。话虽这么说,一个没有偏见的物理学家也许会预料到,存在着一个更小的作用范围。在许多情况下,爆炸的效应将不是一种正常的异构转变,而是染色体的一种损伤,通过巧妙的杂交,使得没有受到损伤的那条染色体(即第二套染色体中与受损伤的染色体对应配对的那一条),被相应位点上的基因是病态的一条染色体所替换时,这种损伤就是致死的。所有这一切,全是可以预期的,而且观察到的也确是如此。
52. X射线的效率并不取决于自发的突变可能性
其他一些特性,如果并没有象图式所预言的那样出现,那么,供给上面讲的致死损伤也就容易理解了。例如,一个不稳定的突变体的X射线突变率,平均起来并不高于稳定的突变体。现在,就拿供给30个电子伏那里的爆炸来说,所需的阈能不管是大还是小,比如说,1伏或1.3伏,你肯定不能指望30个电子伏会造成许多差别。
53. 回复突变
有些情况下,转变是从两个方向上来研究的,比如说,从一个确定的“野生”基因变到一个特定的突变体,再从那个突变体变回到野生基因。这种情况下,自然突变率有时几乎是相等的,有时却又很不相同。乍看起来,这是难以理解的,因为这两种情况下要克服的阈似乎是相等的。可是,它当然不是这种情况,因为它必须根据开始时的构型的能级来计算,而且野生基因和突变基因的能级可能是不同的。
总之,我认为德尔勃留克的“模型”是经得起检验的,我们有理由在进一步的研究中应用它。

No comments:
Post a Comment