| |
數學沒有物理是瞎子,物理沒有數學是跛子。
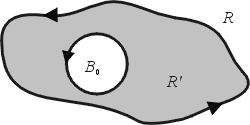
電通量 (flux) 或流體流通過曲線 C 之通量,
學習數學的經驗告訴自己「數學是很容易忘的」。這其中的原因乃是因為我們所學的數學是定義、定理、證明,這種三段式的數學。沒有動機,缺乏直觀,如此的數學如果你不曾打退堂鼓我還真的佩服,在這篇文章我們將以直觀的角度從幾何與物理的觀點來討論 Green 定理。 微積分基本定理可說是微積分最重要的結果之一,而線積分是一維積分的推廣, 因此我們面對線積分是否有相類似的結果:
線積分與雙重積分 (double integral) 之關係為何?
其答案是肯定的──Green 定理:
沿著封閉曲線 C 之線積分可化為 C 所圍區域  之一般雙重積分(面積分)。 之一般雙重積分(面積分)。
這個定理最早出現是由英國自我教育的數學物理學家 George Green(1793~1841)於1828年研究電學 (electricity) 與磁學 (magnetism) 所發現的,當然後來高斯 (Gauss) 等人也發現這結果,Green 的結果讓我們覺得非常之興奮,也更體會伽利略所言
數學是瞭解大自然的語言。
學數學若知道一些物理讓妳(你)永遠不曾感到孤單。 Green 定理是數學分析中最重要的定理之一,而在三維與更高維空間的推廣──Stokes 定理與散度定理 (Divergence Theorem) 則構成了應用數學的基礎
Green 定理與應用 (第 2 頁) 林琦焜
| |
.原載於數學傳播第二十一卷第四期
.作者當時任教於成功大學數學研究所
‧對外搜尋關鍵字 |
| |
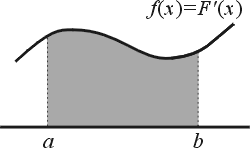
微分與積分的關係這是微積分的主要房角石,實際上這正是牛頓與萊布尼茲對微積分最重要的貢獻,透過這個重要結果──微積分基本定理 (fundamental theorem of calculus),我們明白微分與積分實際上是互為一體兩面,彼此是互相可逆的 (inverse)。 微積分基本定理:
![$f : [a,b] \rightarrow \mathbf{R}$](http://episte.math.ntu.edu.tw/articles/mm/mm_21_4_03/img2.gif) 為一連續函數且 F'=f 則 為一連續函數且 F'=f 則
這定理告訴我們要計算積分值 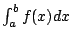 僅需求得函數 f 之原函數 (primitive, 或 antiderivative) F 即可。另外也說明了底下之事實: 僅需求得函數 f 之原函數 (primitive, 或 antiderivative) F 即可。另外也說明了底下之事實:
一個函數之微分的積分值等於該函數之邊界值的差。
換句話說方程式(1)把區間的積分與作用於其「零維」(zero dimension) 邊界之上的「積分」(零維的積分是該點之值)連繫起來,這零維的邊界是兩個端點 a 與 b。
| | |
| |
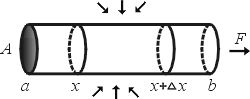
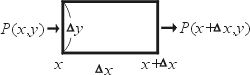
公式(1)我們可以比擬如下:如圖所示,假設有一根直的管子其截面積等於 A 是固定不變,有水在管內流動與流速為 F(X),另外由於管壁非完全封閉因此管壁四周同時也有水滲入(或滲出),我們想問的是此滲入率為多少?(假設水的密度始終等於 1)我們取其中一段 ![$[x,x+\Delta x]$](http://episte.math.ntu.edu.tw/articles/mm/mm_21_4_03/img5.gif) 來看,在單位時間內滲入到這段管子的水量必須等於沿管子方向流出的水量與流進的水量之差 來看,在單位時間內滲入到這段管子的水量必須等於沿管子方向流出的水量與流進的水量之差
因此單位管長內水的滲入率為
若是整個區間 [a,b] 則全部滲入管內之水量為
故
由以上之分析可知微積分基本定理之物理本質就是守恆律 (conservation law)。
|
Green 定理與應用 (第 3 頁) 林琦焜
| |
.原載於數學傳播第二十一卷第四期
.作者當時任教於成功大學數學研究所
‧對外搜尋關鍵字 |
| |
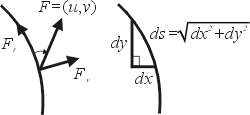
一質點受一變化的力作用而沿一已知曲線移動,而求其所作的功 (work),就自然導致所謂的線積分。 平面上任意向量 F=(u,v),而其沿著曲線切向量 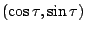 , 法向量 , 法向量 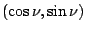 之分量分別為 之分量分別為
因為 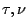 為互餘 為互餘
而單位切向量、單位法向量為
如果將 F 視為力,則線積分
所代表的意義就是功 (work)。其次是若將 F 視為電流密度 (current density) 或流體速度,則線積分
所代表的意義就是電通量 (flux) 或流體流通過曲線 C 之通量,我們在後面還會針對這兩個量作更深入之探討。
|
---------------
Green 定理與應用 (第 4 頁) 林琦焜
| |
.原載於數學傳播第二十一卷第四期
.作者當時任教於成功大學數學研究所
‧對外搜尋關鍵字 |
| |
Green 定理基本上是線積分與面積分之關係,實際上就是微積分基本定理的推廣。 Green 定理:
令 C 為平面上一分段平滑的封閉曲線而其所圍區域為  ,假設函數 P(x,y), Q(x,y) 為連續且一次偏導數也連續則等式成立 ,假設函數 P(x,y), Q(x,y) 為連續且一次偏導數也連續則等式成立
| | |
| |
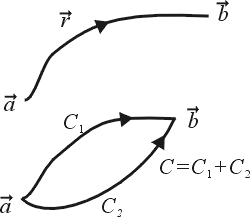
由於曲線 C 的變化可大可小一般而言並沒有明顯的參數式,因此無法直接求線積分,然而我們可利用逼近 (approximation) 的概念來處理,這正是數學尤其是分析 (analysis) 的主要技巧。
長方形 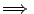 多邊形 多邊形 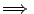 
I.  為一長方形 為一長方形
 之邊界 C = C1 + C2 + C3 + C4 之邊界 C = C1 + C2 + C3 + C4
因此利用微積分基本定理可得
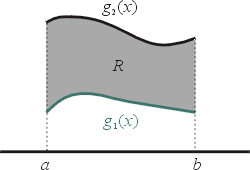
II. 假設  可表為 可表為
我們分別處理 P(x,y) , Q(x,y)
同理可得
兩者合併
這就是 Green 定理,提供了我們關於線積分與面積分之關係,但這個逼近方法有個限制就是曲線 C 必須是有長度曲線 (rectifiable curve),而且還要用到一致收斂 (uniformly convergent) 的概念。對於更一般的區域 Green 定理仍然是對的,但已經超過微積分的範圍,讀者有興趣可參考微分幾何方面的書。
- 例題 1: 利用 Green 定理計算線積分
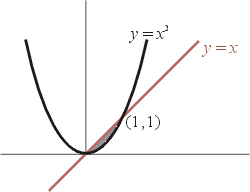
其中曲線 C 是由拋物線 y=x2 與直線 y=x 所圍區域之邊界。
解:要直接計算線積分勢必要將 C 化為參數式,然而利用 Green 定理取
則
因此
Green 定理說明一封閉曲線 C 之線積分與 C 所圍區域之面積分(雙重積分)之關係,因此在特殊情形之下,線積分之幾何意義為「面積」;例如取
則由 Green 定理知
通常可取 P,Q 如下:
- 系: 區域
 由分段平滑的封閉曲線 C 所圍成,其面積為: 由分段平滑的封閉曲線 C 所圍成,其面積為:
- 例題2: 試求橢圓
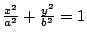 之面積。 之面積。
解:將橢圓表為參數式
利用系之結果得
為著更深入討論 Green 定理,我們再計算一個例題並從其中得到靈感。
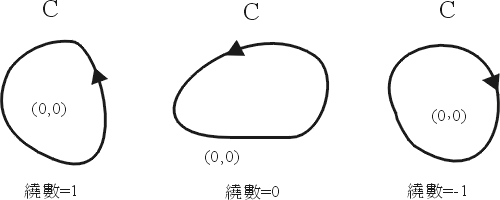
- 例題 3: 已知 C 為任意封閉平滑曲線,試求線積分
解:首先假設 (0,0) 並不包含在 C 之內部,則
因此由 Green 定理知
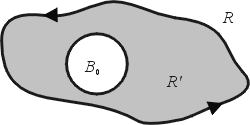
其次,若 (0,0) 在 C 之內部,此時 (0,0) 為一奇異點 (singularity),克服這點的方法就是「避開它」,作一個半徑為 ρ,以 (0,0) 為圓心的圓  考慮區域 考慮區域
由於  並不包含 (0,0),因此利用前面的推論; 並不包含 (0,0),因此利用前面的推論;
但  ,故 ,故
註 1:此處積分值為 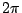 表示曲線 C 繞了奇異點 (0,0) 一圈,而積分值等於 0 則是沒有繞到 (0,0),這所對應的便是複變函數理論的繞數 (winding number),在流體力學則是環流 (circulation)。 表示曲線 C 繞了奇異點 (0,0) 一圈,而積分值等於 0 則是沒有繞到 (0,0),這所對應的便是複變函數理論的繞數 (winding number),在流體力學則是環流 (circulation)。
註 2:證明的過程中我們發現沿著曲線 C 之線積分等於沿著圓周 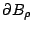 之線積分,這裡面的數學本質就是同倫理論 (homotopy theory),因此 Green 定理可推廣到單連通區域 (simply connected region),而這正是複變函數論研究的一重要主題,同時也說明複雜的曲線之線積分可化為簡單的曲線之線積分(例如圓周的線積分),這就是數學的精神──將複雜的問題化為簡單的問題。 註 3:若 C1,C2 為任二條不相交的分段平滑封閉曲線而且都繞過原點 (0,0),則 之線積分,這裡面的數學本質就是同倫理論 (homotopy theory),因此 Green 定理可推廣到單連通區域 (simply connected region),而這正是複變函數論研究的一重要主題,同時也說明複雜的曲線之線積分可化為簡單的曲線之線積分(例如圓周的線積分),這就是數學的精神──將複雜的問題化為簡單的問題。 註 3:若 C1,C2 為任二條不相交的分段平滑封閉曲線而且都繞過原點 (0,0),則
這除了同倫理論之外,直接的意義就是該線積分對於形變 (deformation) 是一不變量。另外我們可透過極座標 (polar coordinate) 來看;令
則被積分函數 (integrand) 成為
因此這個線積分實際上就是在測量沿著曲線 C(逆時針方向)角度之變化量,當然若是繞了一圈則其變化量為 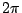 ,若是順時針方向繞了一圈則其變化量為 ,若是順時針方向繞了一圈則其變化量為 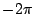 ,這個概念就是前面所說的繞數 (winding number)。 ,這個概念就是前面所說的繞數 (winding number)。 | | |
| |
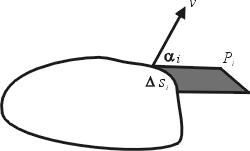
Green 定理也可透過物理的角度來認識:令  為平面上的平滑曲線 C所圍之單連通區域,設 C 可表為 x=x(t), y=y(t) 之參數式,而向量 為平面上的平滑曲線 C所圍之單連通區域,設 C 可表為 x=x(t), y=y(t) 之參數式,而向量
表示流體的速度,我們想計算流體經過邊界 C 之通量 (flux),仿照線積分將曲線 C 分為若干小段而看其中一段;首先是 x 分量通過  之通量(斜線部分之面積)為 之通量(斜線部分之面積)為
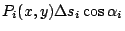 ,其中 ,其中 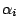 為朝外法向量 ν 與 x 軸之夾角,再將各部份全部加起來並利用 Riemann 和,知 x 軸部分之分量為 為朝外法向量 ν 與 x 軸之夾角,再將各部份全部加起來並利用 Riemann 和,知 x 軸部分之分量為
同理 y 軸之分量為
因此全部之通量為
另一方面我們看小矩形,由於由這矩形左側垂直邊上的流速為 P(x,y),因此單位時間內有 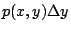 的水流入,而同一時間則約有 的水流入,而同一時間則約有 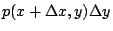 的水流出,所以沿 x 軸方向之單位淨流量為 的水流出,所以沿 x 軸方向之單位淨流量為
令 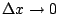 ,得極限 ,得極限 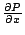 同理沿 y 軸之單位淨流量為 同理沿 y 軸之單位淨流量為 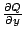 因此單位淨流量為 因此單位淨流量為 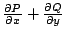 而通過整個區域 而通過整個區域  之全部通量為 之全部通量為
因為水是不可壓縮(假設的),同一時間的水量必須從邊界 C 流出去(質量守恆),故
這再次說明 Green 定理之物理意義為「守恆律」。
|
-------------
Green 定理與應用 (第 5 頁) 林琦焜
| |
.原載於數學傳播第二十一卷第四期
.作者當時任教於成功大學數學研究所
‧對外搜尋關鍵字 |
| |
由(9)與(16)兩式,我們自然而然引進向量的概念:
另外向量場 F 的旋度 (curl) 為
散度 (divergence) 則為
所以 Green 定理((9),(16))可改寫為
分別表示切向量與法向量形式的 Green 定理,而其物理則分別是「功」(work) 與「通量」(flux),(20),(21) 兩式可推廣至更高維數空間,就是通稱的 Stokes 定理與散度定理 (Divergence Theorem)。 為何 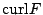 , ,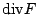 會被稱為旋度與散度呢?我們考慮特殊的區域 會被稱為旋度與散度呢?我們考慮特殊的區域  是以 (x0,y0) 為圓心,半徑是 r 的圓,則由連續性知 是以 (x0,y0) 為圓心,半徑是 r 的圓,則由連續性知
所以旋度是單位面積內之最大環流 (circulation),而散度則是單位面積內之通量(流量之變化),這個形式最大的好處不受座標的影響,如(18),(19)兩式,而且透過(22)式(即利用 Green 定理)我們可證明旋度和散度是與座標無關。 註 1: 如果 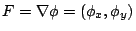 ,向量 (vector) F 為純量(scalar) ,向量 (vector) F 為純量(scalar) 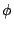 之梯度 (gradient) 則(21)式可改寫為 之梯度 (gradient) 則(21)式可改寫為
函數 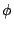 稱為位能函數 (potential function) 而 稱為位能函數 (potential function) 而
則是出名的 Laplace 算子,這是偏微分方程中最重要的算子。 註 2: 若取 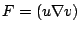 ,則由向量之計算得 ,則由向量之計算得
因此(21)式成為 Green 第一等式
若 u,v 互換,後兩式相減則可得 Green 第二等式
這些等式在偏微分方程中扮演著非常重要的角色。 註 3: Green 定理的最好處理手法是利用微分形式 (differencial forms),我們簡單說明如下:線積分
之被積函數 (integrand) 為一階微分形式 (first order differential form)
L 之全微分 (total differential form) 為
因此 Green 定理可重新寫為微分形式 (differential form)
這個公式同時也說明在區域  之積分及其邊界之積分兩者之關係,而實際上就是微積分基本定理之推廣,當然其精神則是──分部積分 (integration by part)。 之積分及其邊界之積分兩者之關係,而實際上就是微積分基本定理之推廣,當然其精神則是──分部積分 (integration by part)。 |
--------------
|
Green 定理與應用 (第 6 頁) 林琦焜
| |
.原載於數學傳播第二十一卷第四期
.作者當時任教於成功大學數學研究所
‧對外搜尋關鍵字 |
| |
在第五節我們引進了位能函數 (potential function) 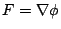 之概念,實際上可經由全微分 (total differential) 來理解 之概念,實際上可經由全微分 (total differential) 來理解
因此
換為微分方程的語言則是「正合」(exact)。 線積分的微積分基本定理: 假設 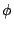 為一可微分函數,且其梯度 為一可微分函數,且其梯度 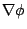 為連續, 為連續, 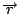 為連接 為連接 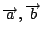 兩點之任意曲線,則 兩點之任意曲線,則
這定理的物理意義(電學的角度):沿著電場上兩點間任一曲線電場所作的功為兩點的電位差,由 Green 定理可知若 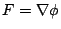 ,C1,C2 為連接 ,C1,C2 為連接 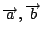 之任意兩條曲線則 之任意兩條曲線則
因此
即線積分與路徑無關 (path-independent),換句話說,將一物體(或質點)由位置 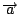 移至位置 移至位置 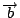 ,力對物體(質點)所作的功,僅和物體(質點)起點位置及終點位置有關,而與其運動所遵循的運動路徑無關,此時我們稱向量場 F 為保守的 (conservative),而 ,力對物體(質點)所作的功,僅和物體(質點)起點位置及終點位置有關,而與其運動所遵循的運動路徑無關,此時我們稱向量場 F 為保守的 (conservative),而 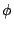 則稱為 F 之位能函數,這定理也告訴我們 則稱為 F 之位能函數,這定理也告訴我們
即位能函數可藉由保守力的線積分而得。
| | |
| |
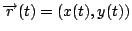 可視為位置向量函數,則速度與加速度分別是: 可視為位置向量函數,則速度與加速度分別是:
設物體的質量為 m,其所受外力的合力為 F,則由牛頓定律知
則對 F 而言從 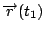 至 至 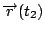 所作的功為 所作的功為
其中 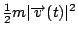 為動能 (kinetic energy), 因此(35)式就是「動能定理」,其物理意義: 為動能 (kinetic energy), 因此(35)式就是「動能定理」,其物理意義:
合力對物體所作的功等於動能的改變量。
如果 F 為一保守力場, 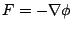 則由線積分的微積分基本定理知: 則由線積分的微積分基本定理知:
則(32)式改寫為
其中 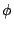 為位能 (potential energy),因此(37)式就是能量守恆定律 (conservation of energy)。 為位能 (potential energy),因此(37)式就是能量守恆定律 (conservation of energy)。 | | |
| |
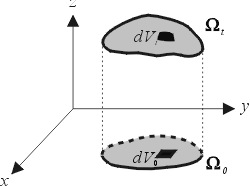
有了速度的概念之後,我們覺得這是很好的時機來闡釋散度 (divergence) 的物理意義。我們可以這麼想像:假設正在喝咖啡,將奶精倒入杯內,最初形成的圖形為  ,而後經由攪拌或其他因素使得 ,而後經由攪拌或其他因素使得  變化,其位置向量為 變化,其位置向量為 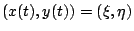 ,速度則為 ,速度則為 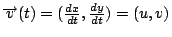 ,經過 t 時間之後 ,經過 t 時間之後 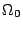 轉換為 轉換為 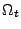 ,我們有興趣的問題是 ,我們有興趣的問題是 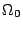 與 與 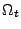 兩者之面積變化為何?(實際上牛頓力學本身就是一種座標變換)我們看其中一小塊 兩者之面積變化為何?(實際上牛頓力學本身就是一種座標變換)我們看其中一小塊 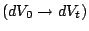 兩者關係為 兩者關係為
其中 J(t) 就是 Jacobian
因此 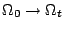 之變化情形,等於是探討 J(t) 的變化,我們假設 之變化情形,等於是探討 J(t) 的變化,我們假設 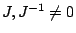 ,即沒有退化的情形(可設 ,即沒有退化的情形(可設  ):由全微分 (total differential) 知 ):由全微分 (total differential) 知
同理可得
J(t) 對 t 微分並利用行列式之性質可得
所以 J(t) 滿足一階微分方程; Euler 展開公式:
這公式稱為 Euler 展開公式 (Euler expansion formula),由微分方程知
由此式顯然可得
因此我們稱一流體為不可壓縮 (incompressible) 其真實意義:
流體經過任何的變換其形狀雖然改變了,但其面積(或體積)卻始終保持不變。
| | |
| |
由例題3 的經驗知線積分
為向量場 F=(u,v) 環繞封閉曲線 C 之環流,利用等式
我們可將前一式表為
假設  為包含 P0(x0,y0) 之區域,則 為包含 P0(x0,y0) 之區域,則
表示單位面積之環流,因此
所以向量場 F 之旋度 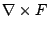 (在 (x0, y0) 之旋度)就是單位面積產生最大環流的量且其方向垂直於 (在 (x0, y0) 之旋度)就是單位面積產生最大環流的量且其方向垂直於 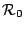 。 。
|
林琦焜
| |
.原載於數學傳播第二十一卷第四期
.作者當時任教於成功大學數學研究所
‧對外搜尋關鍵字 |
| |
- Cauchy 定理:
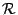 為複數平面上之單連通區域 (simply connected domain),f 為定義在 為複數平面上之單連通區域 (simply connected domain),f 為定義在 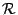 上之單值 (single value) 連續可微且解析的函數,則 上之單值 (single value) 連續可微且解析的函數,則
其中 C 為包含在 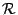 內之任意分段平滑之 Jordan 曲線。 內之任意分段平滑之 Jordan 曲線。
解:假設 f=u+iv , z=x+iy 則複變積分(實際上就是線積分)為
但 f 可微且
因為 u,v 之偏導數為連續,因此可利用 Green 定理分別作用到實部與虛部得
由 Cauchy-Riemann 方程(f 為解析函數)
知上面兩個積分為零,故可結論
複變積分的物理意義可由第三節的討論而得,仿 Cauchy 定理之證明;
當然可以利用 Green 定理將之化為二重積分,(比較(9),(16))
f 之複變積分轉化為向量場 F=(u,v) 之旋度與散度的二重積分,換句話說,透過對向量場 F=(u,v) 的旋度與散度的研究可幫助我們對函數 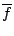 或 f 的認識,實際上 Cauchy-Riemann 方程就是散度與旋度的組合: 或 f 的認識,實際上 Cauchy-Riemann 方程就是散度與旋度的組合:
在近代分析中極負盛名的補償緊緻法 (comnpensated compactness method) 之精神便是,如果向量場之散度與旋度有很好的性質,則原向量場可以得到更好的緊緻性(就是所謂的散度旋度引理 (div-curl lemma))。 | | |
| |
(40)式可視為複數形式的 Green 定理;我們先看看座標變換: 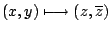
由全微分或連鎖律 (chain rule) 可得
因此Laplace 算子可表為
現在考慮可微分函數 (differentiable function), 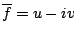 ,則 ,則
另一方面利用微分型式 (differential form) 之公式可得
複數形式的 Green 定理: 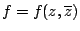 為連續且其偏導數亦為連續則 為連續且其偏導數亦為連續則
其中 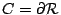 , , 滿足 Green 定理之要求。 如果 f 為解析函數 (analytic function) 則 滿足 Green 定理之要求。 如果 f 為解析函數 (analytic function) 則
分別取實部與虛部等於零,這就是著名的 Cauchy-Riemann 方程式:
再一次得到 Cauchy 定理
因此我們可以說 Green 定理的推廣就是 Cauchy 定理的推廣。 | | |
| |
Cauchy 積分公式:假設 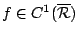 ,則 ,則
這個公式顯然是在一般大學部複變函數理論之 Cauchy 積分公式之推廣。
證明:我們仿前面之例題3計算線積分之方法考慮區域
並且取函數
則由 Green 定理(50)知
因此
令 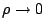 且由連續性之特性可得 且由連續性之特性可得
另一方面由極座標知
所以(55)成為 Cauchy 積分公式(令 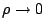 ) )
註 1:Cauchy 積分公式是個古老且優美的結果,通常我們極容易就認定,這就是其終極形式,然而這個「神話」卻於1978年代由 Kerzman 與 Stein 在研究多複變函數 (Several Complex Variables) 所打破,這個結果,我們稱為 Kerzman-Stein 公式,有興趣之讀者可參閱相關資料。 註 2:如果 f 為解析函數 (analytic function), 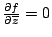 ,則該公式就回到傳統的 Cauchy 積分公式,它告訴我們,對 ,則該公式就回到傳統的 Cauchy 積分公式,它告訴我們,對  內任一點 內任一點 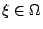 ,函數值 ,函數值 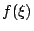 ,可由表為邊界 ,可由表為邊界 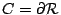 之路徑積分,而這個表現定理 (representation theorem) 也提供了 Cauchy-Riemann 方程 之路徑積分,而這個表現定理 (representation theorem) 也提供了 Cauchy-Riemann 方程 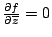 解的公式。 解的公式。 | | |
| |
如果考慮微分方程( 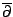 問題) 問題)
Cauchy 積分公式(53)告訴我們右邊第一式可視為齊次解 (homogeneous solution),因此 Cauchy 積分公式(53)同時提議 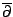 問題(58)之解為 問題(58)之解為
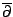 -問題: 假設 -問題: 假設  ,則非齊次 Cauchy-Rieman 微分方程 ,則非齊次 Cauchy-Rieman 微分方程
之解可表為
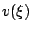 為任意的解析函數 (analytic function) 解:這問題是解決可由複變函數之理論而來,但我們比較喜歡用偏微分方程的技巧,由 Cauchy 積分方式,直觀而言,我們需要處理的是 為任意的解析函數 (analytic function) 解:這問題是解決可由複變函數之理論而來,但我們比較喜歡用偏微分方程的技巧,由 Cauchy 積分方式,直觀而言,我們需要處理的是
顯然可知
因此我們可以假設
c 為一待求之常數,不失一般性可 z0=0 則
直接微分得
因此
換句話說
所以 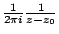 故一基本解 (fundamental solution) 故 故一基本解 (fundamental solution) 故 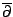 問題之解為 問題之解為
| | |
| |
在複變函數論的發展歷史中,是與流體力學有非常密切之關係,特別是二維穩定、不可壓縮、無旋度、不具黏性的流體 (steady two-dimensional flow of an incompressible, irrotational, inviscid fluid) 其中最著名的是 Bernoulli 定律,這定律說明了飛機飛行的原理,是航空史第一個最重要的定律: Bernoulli 定律:
假設 Ω 為 xy-平面上的一個單連通區域 (simply connected domain) 而曲線
則代表 Ω 中一條有長度分段平滑的封閉區線,因此曲線 C 上任一點之單位切向量與單位朝外法向量為
另外假設流體的速度為
則由(43)式可知
實部表示沿曲線 C 之環流,虛部則表示曲線內面積之變化率,由於我們所考慮的是特殊的流體(穩定、不可壓縮、無旋度、不具黏度性)這個假設告訴我們在曲線 C 內唯一作用到流體的力是流體本身的壓力(法向量方向)必須等於通過 C 之動量通量 (momentum flux),因此
ρ 表示流體之密度,P 為其壓力,利用關係式
可以將(65)改寫為
最後我們假設流體是均勻的 (homogeneous) 因此  常數,因為 常數,因為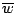 是解析函數,所以 是解析函數,所以  也是解析函數,故由 Cauchy 定理可知 也是解析函數,故由 Cauchy 定理可知
所以(66)式化簡為
由 Morera 定理可結論被積分函數 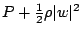 為解析函數, 但由 Green 定理(51)式,可知唯一可能的實值解析函數 (real-valued analytic function) 是常數函數,因此可結論 為解析函數, 但由 Green 定理(51)式,可知唯一可能的實值解析函數 (real-valued analytic function) 是常數函數,因此可結論
- 1. 數學之內容方法及意義(I, II, III);徐氏基金會出版(1970)。
- 2. The Cauchy Transform, Potential Theory and Conformal Mapping; Steven R. Bell; CRC PRESS (1992).
- 3. Introduction to Calculus and Analysis (I, II); R. Courant and F. John; Springer-Verlag (1989).
- 4. Complex Variables; G. Polya and G. Latta; John Wiley and Sons, Inc. (1974).
- 5. Vector and Tensor Analysis; 2nd ed., E.C. Young; Marcel Dekker, Inc. (1993).
|
球面上的測地線和一個平面幾何的問題
張海潮
一八五四年, 年僅二十八歲的黎曼, 在
七十七歲的高斯面前就職演講「論幾何學之
基礎假說」。在這篇演講中, 他解釋了在流形
上為什麼要定出測距的微量元素ds2, 並且
要「建立一個自一原點出發的測地線或最短
曲線系統。」(註一) 用現在的術語來說, 就是
利用測量在局部畫出測地線, 並且利用這些
測地線所形成的座標來(至少) 了解局部的幾
何。
更具體的說, 以地球表面為例,從北極出
發, 沿各條經線往南方走, 這些經線就是測地
線, 它們走了多長可以緯度 表, 走的方向
可以經度 表, 因此ds2 可以d 和d 表成
d 2 + sin2 d 2。(註二) 如果我們觀察一個
緯圓, 亦即等緯度的一個圓, 它等於是由 等
於常數所定義的, 因此d 為0, 此時ds2 就
變成sin2 d 2, 這說明了緯圓的周長會因緯
度而變; 當 是九十度的時候, 它代表赤道,
此時sin 等於1, 說明了赤道緯圓的圓周最
長。(同註二)。
許多微分幾何的教本都會花點篇幅說明
測地線這個名詞並不等價於連結兩點之間的
最短曲線, 原因是測地線起源於局部的測量,
如果只管局部, 那測地線確代表兩點之間的
最短距離。一旦走遠了就不一定是最短的。比
方說, 大家都知道經線是球面上的測地線, 在
同一條經線上的兩點, 有兩個方式連結(圖
一)
.
. . . . . . .
. . .
. . .
. .
. .
. ..
. ..
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
..
..
..
...
................................................................................................................................... ... .. . ..
...
..
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
..
.
..
..
..
...
...
...............
....
..
...
.
..
..
.
..
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
..
..
.
..........................................................................................................................................
....
...
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
. .
.
. .
. . .
. .
. . . .
. . . . . . •
P •
Q
劣
弧
優
弧
圖一
左邊的那一段較短稱為劣弧, 右邊的那一段
較長稱為優弧, 劣弧是最短距離, 但兩個弧都
是測地線。
因此曲面上測地線的意義在數學上就乾
脆定成是滿足測地線方程式的曲線。我以為
這個定義方程式是伯努利在一六九八年給萊
布尼茲的信裡首先提出的。(註三)
這個定義原來是針對在三度空間中的曲
面所提出的, 它把測地線定義為「若將單位切
向量微分則不會有曲面上的分量」。直觀來看,
我們可以把一條曲線想像成是質點以單位速
度(即速率為一) 所走的路徑, 如果它的加速
度向量與曲面垂直, 那麼此時質點速度上的
改變只是為了適應地形而爬上爬下,
對距離來說始終是走最經濟的路線; 換句話
說, 因為加速度的方向即受力的方向, 這個方
向和曲面垂直的時候表示質點唯一的受力來
自曲面對質點的束縛(Constraint) 這樣的
力不會對質點做功, 質點是處在自由運動的
狀態, 自然應該經歷最短的距離。(所以愛因斯
坦在廣義相對論裡認為光走的路徑就是測地
線)。
對一些簡單的曲面, 利用這個定義很容
易發現測地線。拿球面來說, 我們看看經線,
沿經線畫單位長的切向量, 這些切向量微分
以後當然指向經圓的圓心, 也就是球心, 所
以和球面垂直, 因此不僅是經線, 只要是大圓
(圓心和球心重合的圓) 都是測地線。可是要
看出大圓上的劣弧是連結兩端點的最短曲線
其實並不是那麼明顯。雖然我在前段談到伯
努利一六九八年的定義方程式時從物理的角
度出發說明了這個數學定義的合理性, 但是
實際上如果我們硬要在球面上連結甲乙兩點
的大圓之劣弧是甲乙兩點間的最短距離並不
那麼容易證明。
讓我們看一看這個問題的一個比較簡單
的形式: 假設甲乙兩點在一個緯圓上, 而同
時它們也在一個大圓上, 為什麼緯圓上之劣
弧會比大圓上之劣弧長呢? 請看下圖(圖二,
大圓並未畫出)
.
. . . . . .
. . . .
. . .
. . .
. .
. .
. .
. .
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
..
..
...
.................................................................................................................................................... ....... ... ... .. . ...
....
..
..
.
.
..
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
..
.
..
.
..
.
..
..
...
...
....
................
....
...
..
..
..
..
.
..
.
..
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
..
..
...
.....
...................................................................................................................................................................
...
..
..
..
.
..
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
. .
.
. .
. .
.
. .
. .
. . .
. . .
. . . . .
. . . . . ......................................................................................................................................................................................................
•
•
•
•
丁
丙
甲
乙
.
.
.
.
..
.
..
.
.
..
.
..
.
.
.
.
.
.
.
..
.
..
.
.
.
.
.
.
.
..
.
..
.
.
.
.
..
.
.
..
.
.................................................................
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . .
圖二
甲, 乙在緯圓(圓心為丙) 上, 又在以丁
同時為球心和圓心的大圓上, 丙圓小半徑短,
因此以甲乙連線段為軸把丙轉到甲乙丁這個
平面上則丙會落在三角形甲乙丁中, 如圖(圖
三)
..
..
.
.
..
.
.
.
..
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
..
.
.
.
..
.
.
...............................................................................................................................................
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
.
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
甲乙
丙
丁
圖三
圖中有兩個等腰三角形,一大一小, 現在
要證明甲丙·(角丙) 大於甲丁·角丁, 也就是
相應的兩個劣弧之間應有的大小關係。這個
證明不難, 可是一定要用微積分, 雖然表面上
看來不牽涉到。再變形一下, 看看下圖(圖四,
可以說是圖三的左半邊), |
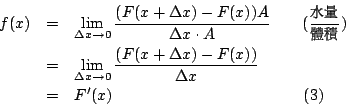
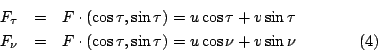
![\begin{displaymath}
\begin{array}[t]{c}
\oint_{C} F_\nu ds = \oint_C udy - vdx \...
...\fontseries{m}\selectfont \char 190}) }
\end{array} \eqno{(8)}
\end{displaymath}](http://episte.math.ntu.edu.tw/articles/mm/mm_21_4_03/img17.gif)

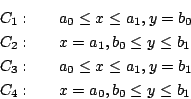
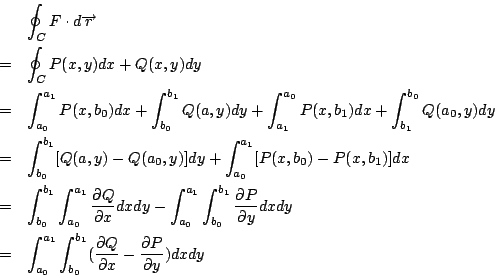
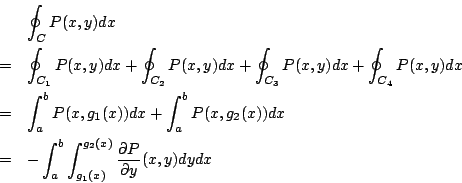

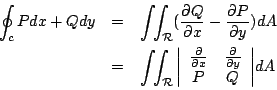
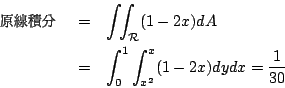
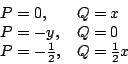
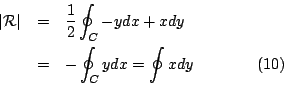
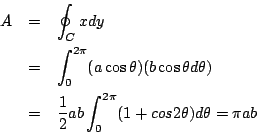
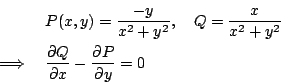
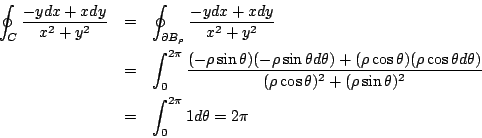
![\begin{eqnarray*}
& &\oint_C[P(x,y) \cos(\nu,x) + Q(x,y) \cos (\nu,y)]ds \\
&=&...
...=&\oint_C F \cdot \nu ds , \; v=(\frac{dy}{ds},- \frac{dx}{ds})
\end{eqnarray*}](http://episte.math.ntu.edu.tw/articles/mm/mm_21_4_03/img57.gif)

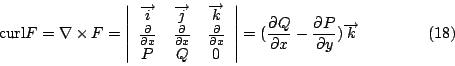

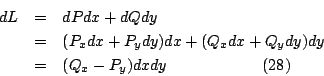
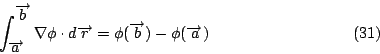
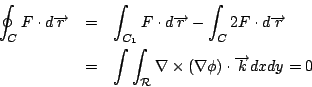
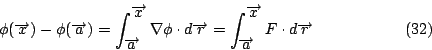
![\begin{displaymath}
\begin{array}[b]{lll}
\overrightarrow{v}(t) = & \frac{d\over...
...2x}{dt^2} , \frac{d^2y}{dt^2} \right )
\end{array} \eqno{(33)}
\end{displaymath}](http://episte.math.ntu.edu.tw/articles/mm/mm_21_4_03/img101.gif)
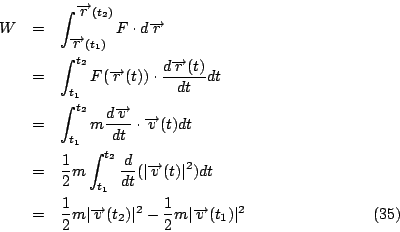
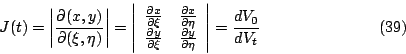
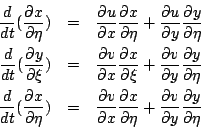

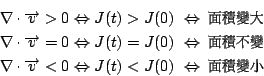
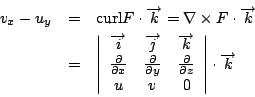
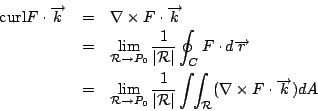


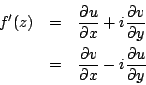
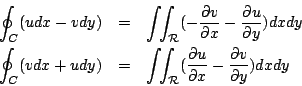
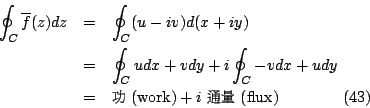
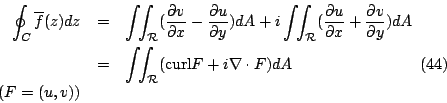
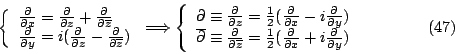
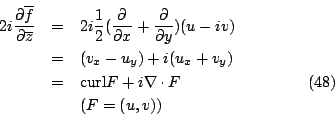
![\begin{eqnarray*}
d[fdz]&=&\frac{\partial f}{\partial z} dz \wedge dz
+ \frac{\p...
...rline{z}} dxdy
\qquad\qquad\qquad\qquad\qquad\qquad \eqno{(49)}
\end{eqnarray*}](http://episte.math.ntu.edu.tw/articles/mm/mm_21_4_03/img150.gif)
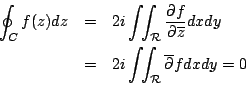
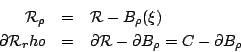


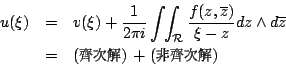
![\begin{displaymath}
\begin{array}[t]{c}
P+ \frac{1}{2}\rho\vert w\vert^2 = \mbox...
...}\fontseries{m}\selectfont \char 98})}
\end{array} \eqno{(60)}
\end{displaymath}](http://episte.math.ntu.edu.tw/articles/mm/mm_21_4_03/img188.gif)

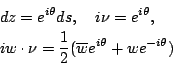
No comments:
Post a Comment