量子物理里面波函数的复振幅是 exp(-E i t / \hbar)
而且计算物理量的平均值的公式也是相似的。
所以引入虚时间 t = - i \hbar / k T，就把量子力学转成了统计力学。而欧式空间转为闵氏空间的方法之一，就是引入虚时间。
这个变换叫 Wick rotation https://en.wikipedia.org/wiki/Wick_rotation ，在此基础上发展出了统计场论，把量子力学和统计力学紧密联系起来。
从基本的统计物理出发的推导请见右边的链接：Boltzmann factor
下面我就不谈推导，只谈理解，我将先给出很初等且极不严谨的理解：
（一）不严谨版。从熵的微观定义说起，S=klnΩ：
在非统计物理的领域，例如在信息学的领域，在统计推断的领域，我们同样会谈到熵，同样可以见到这样的指数形式。熵在统计物理里面意味着无序的程度，在统计推断的领域则意味着系统不确定的程度，如果知道的信息对刻画一个具体的系统只能起很小的作用，那么说明这个信息的质量并不太高，熵是很大的。如果你喜欢这一角度，不妨尝试参考一种理解，这一理解不但可以从统计物理的角度帮助理解这一问题，也可以从统计推断的角度来理解这一问题。统计物理中可以证明，不论在哪种系综下，熵总可以表示为：S=-p ln(p) 的形式。这一定义在统计推断中同样适用。我们根据已知的信息，希望得到一个模型，要让这个模型的约束是最少的，那么就要尝试使系统的熵极大化。在给定几个Lagrangian乘子的约束下，利用变分使熵极大，同样可以得到这一形式，只是这里的系数可能不再是Boltzmann系数而已，指数形式的长相依然存在。这一方法可以参考：Maximum entropy probability distribution，在各类统计学的著作中也有说明。
（三）深入理解的角度
在题主的问题中还出现了对Bose分布理解上的困惑，在初学的阶段，你可以把Bose分布看成是对Boltzmann分布的一个等比级数的求和。
随着学习的深入，再要来真正要来推导Bose分布，Fermi分布，还用能级求和的方法似乎总是显得不够优雅。在对易关系的基础上，考虑算子的含时演化，再将时间替换成t = - i \hbar /kT，整理整理，很自然就得到了Fermi分布和Bose分布。从Wick转动的角度才是一个更好的角度，理解全同粒子的分布，那应当是更基本的东西。
这时候再来看代换t = - i \hbar /kT，或许你已经会觉得它是很自然的了，但是看懂其中的数学并不困难，可是讲清楚其中的物理意义其实还挺困难，可以参考：Thermal quantum field theory，Matsubara frequency，等等维基页面。这一代换得到的有限温度的量子统计的结论可以被实验验证。时间与温度的这种联系可能是因为非对易关系所导致的表现在时间箭头与熵的某种联系。 显示全部
下面我就不谈推导，只谈理解，我将先给出很初等且极不严谨的理解：
（一）不严谨版。从熵的微观定义说起，S=klnΩ：
- Boltzmann常数k可以将一个微观的定义和一个宏观的量联系起来（在这一意义上，它类似于Avogadro常数），例如在能均分定理中，温度是宏观的量，平均的动能是一个微观的定义。
- 对数则使得熵从微观状态数这样一个总是需要作乘法的量，变成了一个可加的量。
- 第一步，现在我们需要把能量（微观）和温度（宏观）联系起来，那么有E/kT；
- 第二步，我们发现这个量的量纲跟熵除以Boltzmann常数的量纲是一样的，不难发现这仍然是一个可加的量，微观状态的占据数应该是一个可乘的量，那么在熵的定义时我们取了对数，这里逆回去，变成指数，于是有exp(E/kT)；
- 第三步，检查一下，发现似乎搞错了，这样会导致E等于无穷的时候占据数无限大，这显然是不合理的，E等于无穷的时候应该占据数为0，粒子倾向于在低能量处占据，那么加上一个负号，得到正确的Boltzmann因子。
在非统计物理的领域，例如在信息学的领域，在统计推断的领域，我们同样会谈到熵，同样可以见到这样的指数形式。熵在统计物理里面意味着无序的程度，在统计推断的领域则意味着系统不确定的程度，如果知道的信息对刻画一个具体的系统只能起很小的作用，那么说明这个信息的质量并不太高，熵是很大的。如果你喜欢这一角度，不妨尝试参考一种理解，这一理解不但可以从统计物理的角度帮助理解这一问题，也可以从统计推断的角度来理解这一问题。统计物理中可以证明，不论在哪种系综下，熵总可以表示为：S=-p ln(p) 的形式。这一定义在统计推断中同样适用。我们根据已知的信息，希望得到一个模型，要让这个模型的约束是最少的，那么就要尝试使系统的熵极大化。在给定几个Lagrangian乘子的约束下，利用变分使熵极大，同样可以得到这一形式，只是这里的系数可能不再是Boltzmann系数而已，指数形式的长相依然存在。这一方法可以参考：Maximum entropy probability distribution，在各类统计学的著作中也有说明。
（三）深入理解的角度
在题主的问题中还出现了对Bose分布理解上的困惑，在初学的阶段，你可以把Bose分布看成是对Boltzmann分布的一个等比级数的求和。
随着学习的深入，再要来真正要来推导Bose分布，Fermi分布，还用能级求和的方法似乎总是显得不够优雅。在对易关系的基础上，考虑算子的含时演化，再将时间替换成t = - i \hbar /kT，整理整理，很自然就得到了Fermi分布和Bose分布。从Wick转动的角度才是一个更好的角度，理解全同粒子的分布，那应当是更基本的东西。
这时候再来看代换t = - i \hbar /kT，或许你已经会觉得它是很自然的了，但是看懂其中的数学并不困难，可是讲清楚其中的物理意义其实还挺困难，可以参考：Thermal quantum field theory，Matsubara frequency，等等维基页面。这一代换得到的有限温度的量子统计的结论可以被实验验证。时间与温度的这种联系可能是因为非对易关系所导致的表现在时间箭头与熵的某种联系。 显示全部
统计物理中的
主要在正则系综（canonical ensemble）出现，而这系综出现在粒子数恒定及可与外界交换能量的系统，而外界与系综已形成热平衡（thermal equilibrium）状态。
第一，由于已达至热平衡，外界和系统的能量／粒子数是相同的，所以系统的总能量可说已定；第二，统计力学中，所有微态（microstate）的机率都是相同的。基于这两点，可证明是此系综的分佈，具体证明已由 @lee aichi给出。
我们可以用一个电脑模拟实验去理解。假设有N粒子，而由热平衡所定下的总能量为E，假设能量是量子化（quantized）的，而假设
。那粒子的能量分佈是否
？如果这假设成立，
。
那每粒子的平均能量为
及其涨落（fluctuation）为
做点代数，可知
...(1)
和
...(2)
大家可到canonical_ensemble/sim_mr_canonical.py at master 路 stephenhky/canonical_ensemble 路 GitHub，参第一个函数raw_sim_particle_levels看具体做法。做完模拟后分析数据，可验证(1)（参图一）和(2)（参图二）。
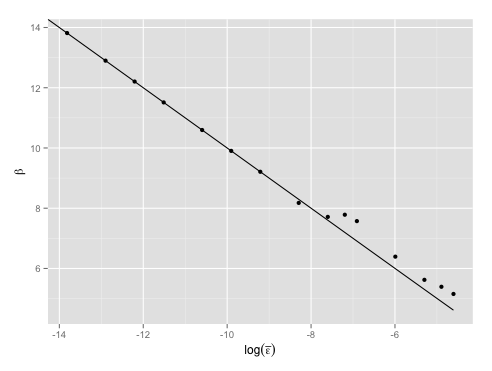图一
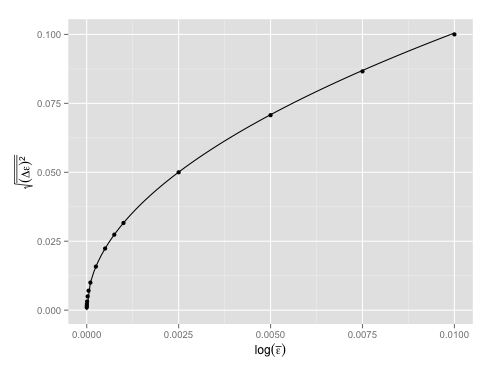图二
从(1)可知，
跟热平衡能量有关，从热力学可知，
。
在量子力学中，
是酉矩阵（unitary matrix），描述量子态的随时间演化。由于统计力学和量子力学这一点的相似性，用Wick’s rotation，我们可以往返量子力学和统计力学。这是量子场论和统计场论的联系。由于量子场论的时间通常由0至无穷大，但统计场论的则由0至
，我们出现了Matsubara frequency，其场论中的和可用简单的複变（complex variable）手法计算出，要注意玻色粒子（bosons）和费米粒子（fermions）是不同的。
但如果我们想知道一个统计系统的时间的演化，我们怎样把和放在一起？我们要借助Keldysh formalism。一个开放量子系统（open system）的时间演化，可用influence functional（参Feynman and Hibbs最后一课），当中有向前和向后两个路径的组合。如果是多粒子系统，这路径会沿着虚轴走。可参看以下书籍：
1. Condensed Matter Field Theory: Alexander Altland, Ben D. Simons: 9780521769754: Amazon.com: Books 第11课
2. Quantum Mechanics and Path Integrals: Emended Edition (Dover Books on Physics): Richard P. Feynman, Albert R. Hibbs, Daniel F. Styer: 9780486477220: Amazon.com: Books 第12课
3. Nonequilibrium Quantum Field Theory (Cambridge Monographs on Mathematical Physics): Esteban A. Calzetta, Bei-Lok B. Hu: 9780521641685: Amazon.com: Books
注：函数raw_sim_particle_levels的实现：
第一，由于已达至热平衡，外界和系统的能量／粒子数是相同的，所以系统的总能量可说已定；第二，统计力学中，所有微态（microstate）的机率都是相同的。基于这两点，可证明
我们可以用一个电脑模拟实验去理解。假设有N粒子，而由热平衡所定下的总能量为E，假设能量是量子化（quantized）的，而假设
那每粒子的平均能量为
做点代数，可知
和
大家可到canonical_ensemble/sim_mr_canonical.py at master 路 stephenhky/canonical_ensemble 路 GitHub，参第一个函数raw_sim_particle_levels看具体做法。做完模拟后分析数据，可验证(1)（参图一）和(2)（参图二）。
图一图二从(1)可知，
在量子力学中，
但如果我们想知道一个统计系统的时间的演化，我们怎样把
1. Condensed Matter Field Theory: Alexander Altland, Ben D. Simons: 9780521769754: Amazon.com: Books 第11课
2. Quantum Mechanics and Path Integrals: Emended Edition (Dover Books on Physics): Richard P. Feynman, Albert R. Hibbs, Daniel F. Styer: 9780486477220: Amazon.com: Books 第12课
3. Nonequilibrium Quantum Field Theory (Cambridge Monographs on Mathematical Physics): Esteban A. Calzetta, Bei-Lok B. Hu: 9780521641685: Amazon.com: Books
注：函数raw_sim_particle_levels的实现：
def raw_sim_particle_levels(N, totalE, R=float('inf')):
"""
Simulate the energy levels for all particles, given
there are N particles, totalE unit of energies and R
energy levels.
Args:
N (int): Total number of particles.
totalE (int): Total units of energies.
R (int or float, optional): Number of energy levels. Defaults to float('inf').
Returns:
ndarray: An array (ndarray) of N elements storing the energy levels of all the
N particles in the simulation.
"""
partlevels = np.zeros(N)
for i in range(totalE):
avail_part = np.where(partlevels<(R-1))[0]
#idx = np.random.choice(avail_part)
idx = avail_part[np.random.randint(0, high=len(avail_part))]
partlevels[idx] += 1
return partlevels
1楼答非所问吧。。我真不是和1楼做对，听说1楼来了以后知乎民科少了很多，但一楼的答案 也常有偏激，片面，主观和审题失误之处，我建议他多找几个水平相同的物理系学生互相进步（不是我，我水平太低==）
问题问的是为什么分母上常见kT，和波函数无关（量子力学和场论不会告诉你为什么有kT）。为什么会有kT，这和统计力学的推导有关系。你可以理解为kT是温度所表征的能量，参见能量均分定理。那么E/kT就是粒子能量和温度能量之比；粒子态的能量越比环境温度能量高，其出现的概率就越小，这就是boltzmann分布的意思。环境温度就好比一个大热炉，提供取之不尽的kT能量；粒子分布就好比这个大热炉中的涨落。
问题问的是为什么分母上常见kT，和波函数无关（量子力学和场论不会告诉你为什么有kT）。为什么会有kT，这和统计力学的推导有关系。你可以理解为kT是温度所表征的能量，参见能量均分定理。那么E/kT就是粒子能量和温度能量之比；粒子态的能量越比环境温度能量高，其出现的概率就越小，这就是boltzmann分布的意思。环境温度就好比一个大热炉，提供取之不尽的kT能量；粒子分布就好比这个大热炉中的涨落。
大神们都说的很透彻了。补充一点，关于k的。
热力学对两个系统的温度做明确的限定就只有温度的比值（T1/T2，e.g卡诺循环），所以（熵无量纲）能够随意的让温标乘以常数。比如说Kelvin scale和Rankine scale（温标的零点确定）。所以我们愿意的话也可以选一个温标，让k=1。
《thermodynamics and an introduction to thermostatistics》,Herbert B.Callen,Chapter 2.6 temperature units,
热力学对两个系统的温度做明确的限定就只有温度的比值（T1/T2，e.g卡诺循环），所以（熵无量纲）能够随意的让温标乘以常数。比如说Kelvin scale和Rankine scale（温标的零点确定）。所以我们愿意的话也可以选一个温标，让k=1。
《thermodynamics and an introduction to thermostatistics》,Herbert B.Callen,Chapter 2.6 temperature units,
txz 赞同
个人拙见，这个公式暂且不提，先看看其他符合波尔兹曼分布的公式，比如在势垒为ΔG的波尔兹曼分布下，n=n○exp(-ΔG/kT)，可以看作由于势垒存在而出现的一种必然的统计学结果。势垒ΔG可以看作外因，温度T可以看作内因，而k则是一个换算单位，体现出势垒、内部普遍能量状态与状态分布的相关联系。
这个式子还可以与标准正态分布联系起来，可以参考材料科学的扩散理论，具体的就不推导了。但是可以看到的是内外因与分布的统计学关系，这一点对于世间万物是普遍适用的。
这个式子还可以与标准正态分布联系起来，可以参考材料科学的扩散理论，具体的就不推导了。但是可以看到的是内外因与分布的统计学关系，这一点对于世间万物是普遍适用的。
这个问题我是从量子隧穿上理解这个式子的，T是温度，在热力学中反映粒子所具有的能量，E是势垒高度，可以理解为一堵墙。整个指数项反映的是具有一定能量的粒子跨过高度为E的势垒的概率。玻尔兹曼分布按这个方式就很好理解，固体物理中导带电子分布也可以从这个方向理解，当然还有电子跃迁概率。手机打的排版不好请见谅！
我觉得这只是因为你对这个函数熟悉，心理学里面有个效应，大概说当你注意到什么时你会更加注意到。比如椭圆函数也在各个领域里面常见，看到椭圆函数就应该想到环面（我没仔细检查过），就像看到pi就必定有圆存在一样，但前者毕竟不如三角函数这么普及，这让我联想到了问为什么规范群是那几个：因为简单，所以被你观测到了。
1/[exp(E/kT)-1]这个其实和exp(-E/kT)很不像，虽然都是单周期函数，但前者是伯努利数的母函数，因此自然也可以简单和Riemann zeta函数联系上（因为这两个没什么区别），而伯努利数的数论意义更大。在统计物理里面也恰恰是因为1/[exp(E/kT)-1]的奇点行为导致了BEC（希望我没记错- -），另外Fermi因子1/[exp(E/kT)+1]是欧拉数的母函数，题主应该记得统计物理的推导里面也会出现zeta函数作为常数因子。也可以考虑1/[exp(E/kT)+k]，对应的我忘记名字了= =Riemann zeta函数有各种意义的推广，这个记得半导体物理里面会出现？（瞎说的- -）
另外吐槽你们这些随随便便做Wick转动的= =
1/[exp(E/kT)-1]这个其实和exp(-E/kT)很不像，虽然都是单周期函数，但前者是伯努利数的母函数，因此自然也可以简单和Riemann zeta函数联系上（因为这两个没什么区别），而伯努利数的数论意义更大。在统计物理里面也恰恰是因为1/[exp(E/kT)-1]的奇点行为导致了BEC（希望我没记错- -），另外Fermi因子1/[exp(E/kT)+1]是欧拉数的母函数，题主应该记得统计物理的推导里面也会出现zeta函数作为常数因子。也可以考虑1/[exp(E/kT)+k]，对应的我忘记名字了= =Riemann zeta函数有各种意义的推广，这个记得半导体物理里面会出现？（瞎说的- -）
另外吐槽你们这些随随便便做Wick转动的= =
No comments:
Post a Comment