感觉平行宇宙理论是大家对 Everett III 的最初的理论的一个误解,这个名字也挺奇怪的,多世界理论似乎是 DeWitt 在 Everett 的理论上面发展起来的,不过我没有看过 DeWitt 的理论,所以不确定是不是真的是题目中所描述的那种多世界理论。
不过,至少 Everett 的理论并不是一个可以导致平行世界的理论,而且实际上平行世界理论会跟这套理论的第一基本假设冲突。后人在 Everett 的基础上给出了好几种理论,如果没有改动这个基本假设的话,可以说,都不能支持平行世界的。
## Copenhagen Interpretation
Copenhagen 学派对于量子力学的基本的解释有四条(或者五条六条,取决于用谁的教材……好吧),其中最重要的两条,一条是关于体系的状态是如何演化的,另一条是关于测量的时候会发生什么。
第一条说,体系是按照 Schrodinger 方程来演化的
第二条是说,当我们去测量一个体系的时候,体系会坍缩到我们要测量的量的本征态上,如果数学上看这个被测量量的本征态是离散的,那么我们测量无穷次,也只会得到一系列的离散的测量值。
Copenhagen 解释最初应该是用波函数来进行的,但是后来随着时间发展,大家开始使用一个抽象的 Hilbert 空间的矢量来代指状态,这个抽象的状态本身没法诠释物理,我们需要把这个投影到我们选定的有物理意义的基矢上才可以作为一个可以用来解释物理的量,例如波函数。
所以实际上,即便是 Copenhagen 解释,现在也已经发展的挺完善了,数学上也很漂亮。(真的很漂亮,我原来本科的时候读的是中文的量子力学教材,曾谨言的什么的,那时候觉得量子力学的数学很丑陋。后来读了 Dirac 和Shankar 的书,顿时震惊了。国内中文的量子力学教材需要更新啦~ Dirac 那套真的是应该从头就教起。当然,好的大学肯定是好教材啦,我没机会体会,只能羡慕了。)
但是,这套体系有个问题。大家注意到这里有个关于测量的理论。这就有个问题是,这套理论把测量者放在了一个特殊的位置上了。
所以当年 Everett III 就提出了这样的一个疑问,如果我们有个孤立系统,这个系统里面是一个观测者在观测一个体系,那么这个体系会如何演化?按照 Copenhagen 的诠释,这个体系的演化很诡异,因为测量会导致坍缩,这个体系根本不遵从 Schrodinger 方程了。
Everett III 就把观测者从这个特殊的地位上踢下来了。
## Many-Worlds Interpretation
Everett III 就说,好,那我们就直接假定任何的孤立系统都按照 Schrodinger 方程来演化。
也就是说,不管是个什么孤立体系,即便是整个宇宙,也要按照 Schrodinger 方程来演化。
这样的结果就是,我们所在的宇宙,包括我们自己,整个体系都是量子的,可以是很多物理状态的叠加。
那为什么我们看到的东西有些不是状态叠加呢?这里面就是退相干的功劳了,我们看到的很多是退相干的结果,这是 Everett III的理论的一个很优美的地方,也就是我们不再需要一个关于测量的假设了,而是直接使用退相干来计算有些内部的观测结果。
(这个不把观测者剥离出来,只看整体的想法,我在本科的时候,写过量子的课程论文,那只是一个想法,才疏学浅,很多东西不知道,也不会算,也没想到这样一个简单的假设就可以完成任务,更没有把数学框架建立起来,也就是说没法计算,那之后也没有深究这个问题。这大概就是普通人和牛人的差别吧。)
## 平行世界
平行世界大概就是从这个想法扩展来的。如果我们的整个宇宙都是一些态的叠加,那么我们每次退相干的观测结果,就是选取了世界的一条分支,同时世界存在其他的分支,就是其他的观测结果。
例如我们的 Schrodinger 的猫的实验。
假定我们和猫换一下位置,有一只猫打开了盒子进行测量,而整个世界就只有这个盒子和这只猫组成。那么整个系统遵从 Schrodinger 方程,整个世界还应该是我们生与死的叠加,但是猫进行了观测,有了退相干过程,例如猫看到我们还活着。那么如何理解一个外部观者看到的生死叠加的态呢?有人就觉得,外部观者看到的是世界走了其中一条分支,另一条分支是我们死掉了。
但是 Everett III 的理论跟平行世界理论是有冲突的,因为在 Everett III 的理论中,生和死这两个状态是可以出现干涉等等现象的,而平行世界的解释,把两个状态隔离开了了,就不会有生与死的干涉了。
## 解读
所以我有点倾向于认为,平行世界是对 Everett III的理论的一种错误解读。
## 扩展
1.
不过需要提到的是,在 11 年的时候,Bousso 和 Susskind 合写了一篇文章:
文章大致是说,量子力学里面的 Many-worlds Interpretation 和宇宙学里面的 Multiverse 可以统一起来。
Multiverse 是一个这样的想法。我们研究宇宙学,有个最大的毛病就是,我们只有一个体系可以观测。那么我么得出了这个宇宙的一些性质,有好几种方法去诠释这些结论,有些诠释是基于最可能出现的,另外一些诠释是不管这些的,认为我们的宇宙也可能是一个个例,剑走偏锋。虽然我们不能批判第二种观点,但是第一种是更加容易接受的。
后来有人就提出说,存在很多不同的宇宙,这些宇宙可能是有不同的物理常数,甚至不同的物理规律。当然这些宇宙之间没有关联什么的。
这个就是一个常见的 Multiverse 版本,或者叫做平行宇宙。
Bousso 和 Susskind 的文章就是把上面解释的 量子力学的 Many-worlds interpretation 和宇宙学里面这个看起来完全没有关联的多宇宙联系起来了。
具体的我就不知道了,这个是 String 的内容,啃起来肯定很痛苦。
2.
关于所谓的 Many-worlds interpretation 在物理学界的支持情况,有过一个统计,结果如下:
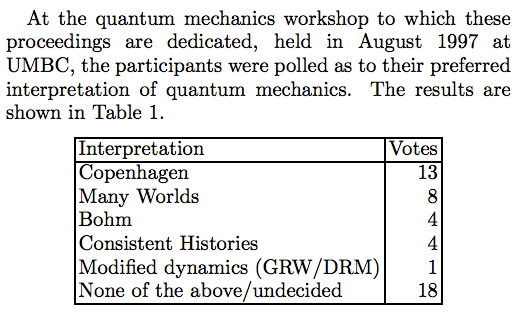
(截取自物理鬼才 Tegmark 的文章:http://arxiv.org/abs/quant-ph/9709032 这个文章也是个挺好玩的科普,可以读读看。)
可以看到多世界诠释还是有很多支持的。不过争论犹在,到底谁最后成为正统,还很难说。例如

(这是在 arxiv 的 title 里面搜索 many worlds interpretation 的结果里面的,这两家伙……)
## 总结
返回来回答题目。
按照题目后面的解释,这里的“平行宇宙“指的是量子力学的多世界诠释。如果是这样,似乎是没有理论支持人不死(被称作 Quantum Imortality )的,这个在 arxiv 也有篇文章,不过看起来水平不怎样,所以就不贴过了。
如果是指的宇宙学里面的平行宇宙,那传统的观点下看,不同的宇宙压根就没有关联,更不用谈不死了。
不过,上面扩展里面提到了一篇两个大牛的合写的文章,认为量子力学这个多世界和宇宙学的平行宇宙是一会儿事,才能所限,不能展开解释那篇文章。
-----
(因为我本身不做量子力学基本理论,所以所知很少,如果理解有误,还请指出来。)
(本文参考了 http://www.phy.ohiou.edu/~murphy/talks/misc/manyworlds.pdf 这篇文章,以及Everett III 在 RMP 的文章 https://docs.google.com/file/d/0ByjhpSk2nUFpM2R4ZzlDTjYyMGM/edit?usp=sharing )
不过,至少 Everett 的理论并不是一个可以导致平行世界的理论,而且实际上平行世界理论会跟这套理论的第一基本假设冲突。后人在 Everett 的基础上给出了好几种理论,如果没有改动这个基本假设的话,可以说,都不能支持平行世界的。
## Copenhagen Interpretation
Copenhagen 学派对于量子力学的基本的解释有四条(或者五条六条,取决于用谁的教材……好吧),其中最重要的两条,一条是关于体系的状态是如何演化的,另一条是关于测量的时候会发生什么。
第一条说,体系是按照 Schrodinger 方程来演化的
第二条是说,当我们去测量一个体系的时候,体系会坍缩到我们要测量的量的本征态上,如果数学上看这个被测量量的本征态是离散的,那么我们测量无穷次,也只会得到一系列的离散的测量值。
Copenhagen 解释最初应该是用波函数来进行的,但是后来随着时间发展,大家开始使用一个抽象的 Hilbert 空间的矢量来代指状态,这个抽象的状态本身没法诠释物理,我们需要把这个投影到我们选定的有物理意义的基矢上才可以作为一个可以用来解释物理的量,例如波函数。
所以实际上,即便是 Copenhagen 解释,现在也已经发展的挺完善了,数学上也很漂亮。(真的很漂亮,我原来本科的时候读的是中文的量子力学教材,曾谨言的什么的,那时候觉得量子力学的数学很丑陋。后来读了 Dirac 和Shankar 的书,顿时震惊了。国内中文的量子力学教材需要更新啦~ Dirac 那套真的是应该从头就教起。当然,好的大学肯定是好教材啦,我没机会体会,只能羡慕了。)
但是,这套体系有个问题。大家注意到这里有个关于测量的理论。这就有个问题是,这套理论把测量者放在了一个特殊的位置上了。
所以当年 Everett III 就提出了这样的一个疑问,如果我们有个孤立系统,这个系统里面是一个观测者在观测一个体系,那么这个体系会如何演化?按照 Copenhagen 的诠释,这个体系的演化很诡异,因为测量会导致坍缩,这个体系根本不遵从 Schrodinger 方程了。
Everett III 就把观测者从这个特殊的地位上踢下来了。
## Many-Worlds Interpretation
Everett III 就说,好,那我们就直接假定任何的孤立系统都按照 Schrodinger 方程来演化。
也就是说,不管是个什么孤立体系,即便是整个宇宙,也要按照 Schrodinger 方程来演化。
这样的结果就是,我们所在的宇宙,包括我们自己,整个体系都是量子的,可以是很多物理状态的叠加。
那为什么我们看到的东西有些不是状态叠加呢?这里面就是退相干的功劳了,我们看到的很多是退相干的结果,这是 Everett III的理论的一个很优美的地方,也就是我们不再需要一个关于测量的假设了,而是直接使用退相干来计算有些内部的观测结果。
(这个不把观测者剥离出来,只看整体的想法,我在本科的时候,写过量子的课程论文,那只是一个想法,才疏学浅,很多东西不知道,也不会算,也没想到这样一个简单的假设就可以完成任务,更没有把数学框架建立起来,也就是说没法计算,那之后也没有深究这个问题。这大概就是普通人和牛人的差别吧。)
## 平行世界
平行世界大概就是从这个想法扩展来的。如果我们的整个宇宙都是一些态的叠加,那么我们每次退相干的观测结果,就是选取了世界的一条分支,同时世界存在其他的分支,就是其他的观测结果。
例如我们的 Schrodinger 的猫的实验。
假定我们和猫换一下位置,有一只猫打开了盒子进行测量,而整个世界就只有这个盒子和这只猫组成。那么整个系统遵从 Schrodinger 方程,整个世界还应该是我们生与死的叠加,但是猫进行了观测,有了退相干过程,例如猫看到我们还活着。那么如何理解一个外部观者看到的生死叠加的态呢?有人就觉得,外部观者看到的是世界走了其中一条分支,另一条分支是我们死掉了。
但是 Everett III 的理论跟平行世界理论是有冲突的,因为在 Everett III 的理论中,生和死这两个状态是可以出现干涉等等现象的,而平行世界的解释,把两个状态隔离开了了,就不会有生与死的干涉了。
## 解读
所以我有点倾向于认为,平行世界是对 Everett III的理论的一种错误解读。
## 扩展
1.
不过需要提到的是,在 11 年的时候,Bousso 和 Susskind 合写了一篇文章:
The Multiverse Interpretation of Quantum Mechanics
当时注意到这个文章的时候,觉得题目就很诡异,内容更是看不懂……文章大致是说,量子力学里面的 Many-worlds Interpretation 和宇宙学里面的 Multiverse 可以统一起来。
Multiverse 是一个这样的想法。我们研究宇宙学,有个最大的毛病就是,我们只有一个体系可以观测。那么我么得出了这个宇宙的一些性质,有好几种方法去诠释这些结论,有些诠释是基于最可能出现的,另外一些诠释是不管这些的,认为我们的宇宙也可能是一个个例,剑走偏锋。虽然我们不能批判第二种观点,但是第一种是更加容易接受的。
后来有人就提出说,存在很多不同的宇宙,这些宇宙可能是有不同的物理常数,甚至不同的物理规律。当然这些宇宙之间没有关联什么的。
这个就是一个常见的 Multiverse 版本,或者叫做平行宇宙。
Bousso 和 Susskind 的文章就是把上面解释的 量子力学的 Many-worlds interpretation 和宇宙学里面这个看起来完全没有关联的多宇宙联系起来了。
具体的我就不知道了,这个是 String 的内容,啃起来肯定很痛苦。
2.
关于所谓的 Many-worlds interpretation 在物理学界的支持情况,有过一个统计,结果如下:

(截取自物理鬼才 Tegmark 的文章:http://arxiv.org/abs/quant-ph/9709032 这个文章也是个挺好玩的科普,可以读读看。)
可以看到多世界诠释还是有很多支持的。不过争论犹在,到底谁最后成为正统,还很难说。例如

(这是在 arxiv 的 title 里面搜索 many worlds interpretation 的结果里面的,这两家伙……)
## 总结
返回来回答题目。
按照题目后面的解释,这里的“平行宇宙“指的是量子力学的多世界诠释。如果是这样,似乎是没有理论支持人不死(被称作 Quantum Imortality )的,这个在 arxiv 也有篇文章,不过看起来水平不怎样,所以就不贴过了。
如果是指的宇宙学里面的平行宇宙,那传统的观点下看,不同的宇宙压根就没有关联,更不用谈不死了。
不过,上面扩展里面提到了一篇两个大牛的合写的文章,认为量子力学这个多世界和宇宙学的平行宇宙是一会儿事,才能所限,不能展开解释那篇文章。
-----
(因为我本身不做量子力学基本理论,所以所知很少,如果理解有误,还请指出来。)
(本文参考了 http://www.phy.ohiou.edu/~murphy/talks/misc/manyworlds.pdf 这篇文章,以及Everett III 在 RMP 的文章 https://docs.google.com/file/d/0ByjhpSk2nUFpM2R4ZzlDTjYyMGM/edit?usp=sharing )
Where does the wave function of the universe live? Please describe its home
Where does the wave function of the universe live? Please describe its home.
I think this is the Hilbert space of the universe. (Greater or lesser, depending on which church you belong to.) Or maybe it is the Fock space of the universe, or some still bigger, yet more complicated stringy thingy. I will leave it to you whether you want to describe the observable universe, the total universe, or even the multiverse. Please give a reasonably accurate and succinct mathematical description, including at least dimensionality. Thank you. | |||
The wave function lives in the quantum café, see the segment from 3:40 or so to the end of
http://www.youtube.com/watch?v=unJ2ajHH-94More seriously, a wave function is a more special name of the "state vector" which is the element of the Hilbert space Finite-dimensional Hilbert spaces are only used as simplified toy models for some aspects of some physical systems. But they're still very important in theory and practice because realistic situations are often composed of similar small Hilbert spaces by taking tensor products. The two-dimensional Hilbert spaces (e.g. spin-up vs spin-down) seem very simple but they're already very rich and are used as tools to teach quantum mechanics. Quantum computing usually takes place in Hilbert spaces for The Fock space is a special kind of Hilbert space. It is the Hilbert space of a free field theory or, equivalently, an infinite-dimensional harmonic oscillator. One usually defines the free - bilinear - Hamiltonian on the Fock space, too. If we don't say that there's a Hamiltonian, the identity of the Fock space is actually meaningless because all infinite-dimensional Hilbert spaces are isomorphic or "unitary equivalent" to each other. So the Fock space isn't really "something completely different" (or larger) than the Hilbert space; it's a special case of it. The same thing holds for the Hilbert spaces associated with any theory you can think of (describing the world around us or describing a fictitious or hypothetical world), whether it's the Standard Model, the Minimal Supersymmetric Standard Model, or – the most comprehensive theory – String Theory. All these theories, much like any other theories respecting the postulates of quantum mechanics, have their own Hilbert space and all these infinite-dimensional spaces in string theory or a simple infinite-dimensional harmonic oscillator or even a simple Hydrogen atom are actually isomorphic to each other. The theories only differ by different Hamiltonians – or other dynamical laws that describe the evolution in time. Also, one should mention that the actual state of the physical system isn't given by all the information included in an element of the Hilbert space. The phase and the absolute normalization – i.e. the full multiplicative factor that may be complex – is unphysical. So the space of inequivalent "pure states" is actually the quotient Aside from "wave functions" i.e. pure states that are elements of the Hilbert space, up to a normalization, one may also describe a physical system by a more general "density matrix" which lives in the space of Hermitian matrices | |||||||||||||||||||||
|
The word "space" in mathematics is not the same ontological object as physical space. It is sort of equivalent to asking, in classical physics, where is the space of all velocity vectors located? Its not that they are actually somewhere "out there", they are just mathematical abstractions from which useful information can be extracted and inferences can be made unto measurable quantities which are analogous to the abstraction. A vector space (Hilbert, Fock, and many other variations of vector spaces exist!) is a mathematical object which makes convenient many computations one can do with sets of numbers(vectors, matrices, tensors, etc...) endowed with human-invented algebraic properties (closure, commutativity, associativity, etc...). Quantum mechanics makes use of linear algebra almost solely for the fact that one can extract 'spectrum' of eigenvalues which are analogous to the measurable discrete quantities one finds when dealing with such objects.
|
grand design.. – Vineet Menon Apr 10 '12 at 15:27