[PDF]海森堡(Werner Heisenberg) 的測不準原理海森堡(Werner ...
psroc.phys.ntu.edu.tw/bimonth/download.php?d=1&cpid=176...
32 卷1 期. 44. 1927 年2 月,年輕的海森. 堡(Werner Heisenberg)發展. 出了量子理論中的一個主要關. 鍵—測不準原理,意涵極為深. 遠。 1901 年12 月,海森堡誕生.
海森堡不確定性原理的矩陣證明| 線代啟示錄
https://ccjou.wordpress.com/2013/04/.../海森堡不確定性原理的矩陣證...
科學家質疑海森堡的不確定性原理 - 新三才
www.newsancai.com › 科学探索 › 未解之謎
【TED】什么是“海森堡不确定性原理” - AcFun弹幕视频网- 中国 ...
www.acfun.tv › 科学技术
轉為繁體網頁
轉為繁體網頁
這是 http://psroc.phys.ntu.edu.tw/bimonth/download.php?d=1&cpid=176&did=11的 HTML 檔。
Google在網路漫遊時會自動將檔案轉換成 HTML 網頁。
Page 1
雙月刊
32 卷 1 期
44
1927 年 2 月,年輕的海森
堡(Werner Heisenberg)發展
出了量子理論中的一個主要關
鍵—測不準原理,意涵極為深
遠。
1901 年 12 月,海森堡誕生
於德國一個中上階級的學術家
庭。孩童時期,他喜歡數學和
科技小機件,老師們都認為他
極有天賦。1920 年時,他到慕
尼黑大學就讀,在大師索末菲
(Arnold Sommerfeld)的指導
下,兩年內就發表了四篇物理
論文。包立(Wolfgang Pauli,
1945獲得諾貝爾物理獎)當時也就讀於慕尼黑大學,
且僅大海森堡一歲,所以兩人成了討論專業的朋友。
雖然海森堡因必考的實驗問題表現不佳而差一點
無法通過口試,但他還是於 1923 年獲得了博士學
位,論文討論的是流體力學上的一個問題。在得到
博士學位後,他到哥廷根做玻恩(Max Born,1954
年諾貝爾物理獎得主)的助
理,之後又到哥本哈根波耳
(Niels Bohr,1922 年獲得諾
貝爾獎)所主持的研究所跟隨
他一起做了一年研究。
1920 年代初期盛行的量子
論,將原子塑造成是電子沿著
固定量子化的軌道繞著一個原
子核運行,電子可以藉由吸收
或釋放出正確波長的光子而移
至更高或更低的能階。這個模
式在氫原子很適用,但用在大
一點的原子或分子則碰到了問
題,所以物理學家認知到是需
要一個新的理論了。
海森堡反對當時的模型,因為他說既然無法實際
觀察到電子繞著原子核的軌道,就不能說這些軌道
是真的存在,我們只能觀察到被原子釋放或吸收的
光譜而已。自 1925 年起,海森堡即開始研究,試著
找出一種至少在理論上,可以僅基於可觀察到的性
海森堡(Werner Heisenberg)
的測不準原理
海森堡(Werner Heisenberg)
的測不準原理
(譯自APS News,2008 年 2 月)
1927 年 2 月
海森堡(Werner Heisenberg)
譯 蕭如珀、楊信男
Page 2
45
2010.2 / psroc.phys.ntu.edu.tw / PHYSICS BIMONTHLY
本月物理史
質之量子力學。
靠著幾位同事的幫忙與激勵,海森堡發展出了一
個量子力學的新方法。基本上,他採用例如位置和
速度等物理量,但找出了一個新方法來重新加以表
示和運算。玻恩發現海森堡所採用的方法中之奇特
數學為矩陣,這個新的表述方式可用以說明許多已
觀察到的原子特性。
在海森堡得到他以矩陣為基礎的量子力學後不
久,薛丁格(Erwin Schrödinger)也發展出了他的波
動理論表述方式。薛丁格波函數的絕對值平方很快
地被解釋為在某種狀態中找到粒子的或然率,而他
也很快地證明了他的波動表述方式和海森堡的矩陣
方法在數學上是相等的,因此他的方法更受歡迎,
一部份是因為相較於一般不熟悉的矩陣數學,物理
學家還是比較習慣使用描述波動的數學。海森堡因
他自己的矩陣方法不受歡迎而被惹惱,尤其因為當
時老一輩的科學家正相繼退休,而他和其他年輕的
科學家正開始在找他們的第一份教職,自己命運未
卜。
雖然其他的科學家也許覺得波動的方法比較容易
使用,但海森堡的矩陣力學卻很自然地讓他發展出
了測不準原理,也因此聲名大噪。在矩陣數學中,
並非都會是a × b=b × a,對於不可交換的變量組,
例如位置和動量,或是能量和時間,就會產生不確
定的關係。
海森堡還做了一個思考性的實驗,他設想以伽瑪
(γ)射線的顯微鏡測量電子的位置。用來照亮電
子的高能量光子會踢電子一下,但電子動量因之改
變的多寡並不確定,由於解析度愈高的顯微鏡需要
愈高能量的光,這樣光子就會對電子踢得更強一點。
海森堡因此推想,若要更精密地測出電子的位置,
動量就會越無法確定,反之亦然。這種不確定性是
量子力學的一個基本特點,並非受限於任一特別的
實驗設備。海森堡在 14 頁的信中將他的新原理概略
地寫出來,於1927年2月23日寄給包立。同年3月,
他將測不準原理的論文投寄發表。
波耳指出了海森堡思考性實驗中的一些錯誤,但
同意測不準原理本身是正確的,所以將論文刊登了
出來。
此新原理有很深的意涵。以前大家認為只要知道
任一時間中粒子的位置與動量,以及所有作用在其
上的力,就可以至少在理論上預測未來任一時間的
位置與動量。海森堡發現並非如此,因為我們絕無
法真的同時知道粒子確切的位置和動量。
測不準原理很快地成了廣為大家接受的哥本哈
根學派對量子力學詮釋的部分基礎,那年秋天海森
堡和玻恩在布魯塞爾所舉辦的索耳未會議(Solvay
conference)中共同宣布了量子革命的完成。
1927年秋天,海森堡接受萊比錫大學的教授職位,
讓他成了德國最年輕的正教授。1932 年他因量子力
學的研究獲得了諾貝爾獎。海森堡在德國繼續他的
科學研究。第二次世界大戰期間,雖然他不是納粹
黨員,但他是一位愛國的德國公民,所以成了德國
核分裂計畫的領導者,不過他建造原子彈的努力最
後宣告失敗。海森堡此一行為和動機從此一直是爭
論性的話題,他於 1976 年過世。
蕭如珀 自由業
楊信男 台灣大學物理系
E-mail:snyang@phys.ntu.edu.tw
進一步閱讀:David Cassidy, Uncertainty: the Life and Science of Werner Heisenbery (New York: W.H. Free-
man, 1992)
作 者
海森堡(Werner Heisenberg)的測不準原理
海森堡不確定性原理的矩陣證明
本文的閱讀等級:高級
在量子力學裏,不確定性原理[1](uncertainty principle) 表明:粒子的位置與動量不可同時被確定,位置的不確定性 與動量的不確定性
與動量的不確定性  遵守不等式
遵守不等式
 ,
其中
,
其中  ,
,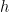 是普朗克常數[2](Planck constant)。海森堡[3] (Werner Heisenberg) 在1927年發表的一篇論文裏,寫下
是普朗克常數[2](Planck constant)。海森堡[3] (Werner Heisenberg) 在1927年發表的一篇論文裏,寫下
 。
雖然他提到這公式可以從對易關係 (稍後將說明) 推導出來,但他並沒有寫出相關的數學論證,也沒有給予
。
雖然他提到這公式可以從對易關係 (稍後將說明) 推導出來,但他並沒有寫出相關的數學論證,也沒有給予  和
和  確切的定義。同年,肯納德 (Earl Hesse Kennard) 首先證明不確定關係不等式,1929年羅伯森 (Howard Percy Robertson) 又從對易關係推導出相同的結論[4]。本文使用現代讀者熟悉的矩陣分析方法證明不確定性原理。由於我對量子力學幾乎一無所知,在提到相關知識的時候均盡量列舉引用出處以方便讀者參照查詢。文中若有錯誤,敬請不吝指正。
確切的定義。同年,肯納德 (Earl Hesse Kennard) 首先證明不確定關係不等式,1929年羅伯森 (Howard Percy Robertson) 又從對易關係推導出相同的結論[4]。本文使用現代讀者熟悉的矩陣分析方法證明不確定性原理。由於我對量子力學幾乎一無所知,在提到相關知識的時候均盡量列舉引用出處以方便讀者參照查詢。文中若有錯誤,敬請不吝指正。

物理學家費曼 (Richard P. Feynman) 說[5]:
既然我們無法從直接經驗去尋找聯想量子世界的運行方式,物理學家選擇何種假設或模型,在很大的程度上取決於個人的想像力與信念。1925年海森堡思考著量子力學的建立基礎,他憶起愛因斯坦曾說[6]:「你的理論決定了你所觀察到的。」這句話啟發他換一個角度看待問題,之後他建議[4]:只有在實驗裏能夠測量到的物理量,稱為可觀察量 (observable),才可以用理論描述其物理行為。當然,並不是所有的物理學家都抱持相同的看法。量子力學的另一位創建者薛丁格 (Erwin Schrödinger) 起初也不認同海森堡的想法 (但很快地,薛丁格於1926年證明波力學與矩陣力學是量子力學的兩種等價描述[6])。儘管未獲得眾多同行的支持,海森堡、玻恩 (Max Born) 與約當 (Pascual Jordan) 仍於1925年共同創立矩陣力學[7](matrix mechanics),大膽假設關於運動的古典概念不適用於量子層級。在原子裏的電子並不是運動於明確的軌道,而是模糊不清,無法觀察到的軌域。海森堡棄絕任何涉及粒子運動軌道的詳細計算,因為運動軌道是無法直接觀察到的。他選擇另一條道路:專注於研究電子躍遷時,所發射的光的離散頻率和強度。他計算出代表位置和動量的無限矩陣,這些矩陣能夠正確地預測電子躍遷所發射出光波的強度[4]。
海森堡從電子轉移的現象歸納出矩陣力學的前提[7]:所有的可觀察物理量都可以用矩陣表示。矩陣的特徵值集合是該物理量可能出現的觀察值。對一般人來說,這絕對是一個聞所未聞的神秘主義。在經驗世界裏,我們頂多用一個隨機變數來表示可觀察量,譬如,投擲骰子可能出現的點數,可是觀察量本身怎麼會跟矩陣扯上關係?況且在工程科學中,矩陣不都是拿來表示線性系統嗎?但量子力學不同於過去的典範,物理學家總是各憑本事編造出許多奇怪的想法企圖描繪原子層次的行為。不論信與不信,我們暫且接受這個瘋狂的假設。因為實驗測量的結果是實數,Hermitian 矩陣的特徵值又都是實數 ( 是 Hermitian 若
是 Hermitian 若  ,見“特殊矩陣 (9):Hermitian 矩陣”),所以我們可以用 Hermitian 矩陣來代表可觀察量。例如,Hermitian 矩陣
,見“特殊矩陣 (9):Hermitian 矩陣”),所以我們可以用 Hermitian 矩陣來代表可觀察量。例如,Hermitian 矩陣
![A=\left[\!\!\begin{array}{rcc} 3&0&i\\ 0&1&0\\ -i&0&3 \end{array}\!\!\right] A=\left[\!\!\begin{array}{rcc} 3&0&i\\ 0&1&0\\ -i&0&3 \end{array}\!\!\right]](https://s0.wp.com/latex.php?latex=A%3D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Brcc%7D++3%260%26i%5C%5C++0%261%260%5C%5C++-i%260%263++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D&bg=ffffff&fg=000000&s=0) 有特徵值
有特徵值  ,說明
,說明  所代表的物理量僅能觀察到這三個值。如果實驗結果是某一特徵值,那麼對應的特徵向量表示在實驗測量之後的一瞬間物理系統所處的特徵狀態。(所謂特徵狀態代表甚麼意思呢?稍後說明。) Hermitian 矩陣的特徵向量是複向量,上例為
所代表的物理量僅能觀察到這三個值。如果實驗結果是某一特徵值,那麼對應的特徵向量表示在實驗測量之後的一瞬間物理系統所處的特徵狀態。(所謂特徵狀態代表甚麼意思呢?稍後說明。) Hermitian 矩陣的特徵向量是複向量,上例為  。這些特徵向量位於向量空間
。這些特徵向量位於向量空間  ,但並不是永遠如此,只是剛巧物理量以
,但並不是永遠如此,只是剛巧物理量以  階矩陣表示而已。舉例來說,設想一個粒子在直線上自由運動,我們用矩陣
階矩陣表示而已。舉例來說,設想一個粒子在直線上自由運動,我們用矩陣 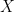 來代表它的位置。由於粒子可能在直線上的任何點,觀察值可以是
來代表它的位置。由於粒子可能在直線上的任何點,觀察值可以是 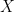 的無窮多個特徵值所成的集合其中任一元素
的無窮多個特徵值所成的集合其中任一元素  。這麼說來,
。這麼說來,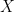 必定是一個無限矩陣 (即無限大階數的矩陣),此矩陣的行空間 (特徵向量存在的空間) 也是一個無限維的向量空間,它的正式名稱叫做 Hilbert 空間 (見 “從幾何向量空間到函數空間”)。在 Hilbert 空間中,向量具有無限維數,無限矩陣改稱為算子 (operator);我們仍然可以計算內積,因此向量長度與正交投影都有良好的定義。不過為方便解釋,以下我們只考慮有限維的幾何座標空間
必定是一個無限矩陣 (即無限大階數的矩陣),此矩陣的行空間 (特徵向量存在的空間) 也是一個無限維的向量空間,它的正式名稱叫做 Hilbert 空間 (見 “從幾何向量空間到函數空間”)。在 Hilbert 空間中,向量具有無限維數,無限矩陣改稱為算子 (operator);我們仍然可以計算內積,因此向量長度與正交投影都有良好的定義。不過為方便解釋,以下我們只考慮有限維的幾何座標空間 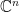 ,讀者不妨想像
,讀者不妨想像  是一個極大的數或令
是一個極大的數或令 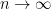 。
。
為了弄清楚海森堡的想法,我們必須知道 Hermitian 矩陣的一些基本性質。在一量子系統中,令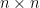 階 Hermitian 矩陣
階 Hermitian 矩陣  代表一個可觀察量,其特徵值為
代表一個可觀察量,其特徵值為  ,對應特徵向量
,對應特徵向量  ,
, 。這些特徵向量構成一組完整的標準正交基底 (orthonormal basis)
。這些特徵向量構成一組完整的標準正交基底 (orthonormal basis)  ,也就是說,
,也就是說, ,
, ,其中
,其中 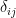 是 Kronecker 記號,
是 Kronecker 記號, 若
若 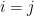 ,
, 若
若  (見“實對稱矩陣可正交對角化的證明”)。令
(見“實對稱矩陣可正交對角化的證明”)。令  維複向量
維複向量  代表量子系統處在的狀態,稱為量子態[8](quantum state)。若量子系統處在某個特徵狀態,
代表量子系統處在的狀態,稱為量子態[8](quantum state)。若量子系統處在某個特徵狀態, ,物理量
,物理量  的觀察值即是特徵值
的觀察值即是特徵值  。但當量子系統不在特徵狀態時,
。但當量子系統不在特徵狀態時, ,
, ,量子態
,量子態  又具有甚麼意義呢?將量子態
又具有甚麼意義呢?將量子態  表示成
表示成
 。
上式左乘
。
上式左乘  可得
可得  ,此即
,此即  在
在  的正交投影值,或者說,
的正交投影值,或者說,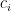 是
是  在
在  的成分或權重。量子態
的成分或權重。量子態  的物理意義可以從組合權重
的物理意義可以從組合權重  來解釋。量子力學稱複數
來解釋。量子力學稱複數 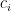 為機率幅[9](probability amplitude),原因是
為機率幅[9](probability amplitude),原因是  即為觀察值
即為觀察值  出現的機率。據此,量子態
出現的機率。據此,量子態  的組合係數絕對值平方
的組合係數絕對值平方  表示在該狀態下,量子系統所有可能出現的觀察值
表示在該狀態下,量子系統所有可能出現的觀察值  的機率分配,故有歸一性
的機率分配,故有歸一性  。因為
。因為  是一標準正交集,
是一標準正交集,
 可知量子態
可知量子態  也滿足歸一性
也滿足歸一性  。當系統處在量子態
。當系統處在量子態  ,如何計算可觀察量
,如何計算可觀察量  的期望值呢?出乎意料外,答案是二次型
的期望值呢?出乎意料外,答案是二次型  。使用特徵方程
。使用特徵方程  ,可得
,可得
 為簡化符號,可觀察量
為簡化符號,可觀察量  在量子態
在量子態  的期望值表示為
的期望值表示為
 。
類似機率學的標準差
。
類似機率學的標準差 ![\sigma=\sqrt{E[(x-\mu)^2]}=\sqrt{E[x^2-\mu^2]} \sigma=\sqrt{E[(x-\mu)^2]}=\sqrt{E[x^2-\mu^2]}](https://s0.wp.com/latex.php?latex=%5Csigma%3D%5Csqrt%7BE%5B%28x-%5Cmu%29%5E2%5D%7D%3D%5Csqrt%7BE%5Bx%5E2-%5Cmu%5E2%5D%7D&bg=ffffff&fg=000000&s=0) ,其中
,其中 ![\mu=E[x] \mu=E[x]](https://s0.wp.com/latex.php?latex=%5Cmu%3DE%5Bx%5D&bg=ffffff&fg=000000&s=0) 是隨機變數
是隨機變數  的期望值,我們定義可觀察量
的期望值,我們定義可觀察量  在量子態
在量子態  的不確定性 (uncertainty) 如下:
的不確定性 (uncertainty) 如下:
 。
關於矩陣力學基礎知識的討論至此告一段落,不確定性原理的證明即將展開。
。
關於矩陣力學基礎知識的討論至此告一段落,不確定性原理的證明即將展開。
1925年,玻恩閱讀了海森堡的論文後,發現位置與動量無限矩陣有一個很顯著的關係──它們不可交換 (或說不互相對易)[4,7]。不確定性原理是下列不互相對易關係的直接結果:
![[Q,P]=i\hbar I [Q,P]=i\hbar I](https://s0.wp.com/latex.php?latex=%5BQ%2CP%5D%3Di%5Chbar+I&bg=ffffff&fg=000000&s=0) ,
其中
,
其中 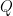 是位置矩陣,
是位置矩陣,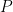 是動量矩陣,
是動量矩陣,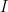 是單位矩陣,
是單位矩陣, 。上式中,
。上式中,![[Q,P] [Q,P]](https://s0.wp.com/latex.php?latex=%5BQ%2CP%5D&bg=ffffff&fg=000000&s=0) 稱為交換子 (commutator,或稱對易算符),定義為
稱為交換子 (commutator,或稱對易算符),定義為
![[Q,P]=QP-PQ [Q,P]=QP-PQ](https://s0.wp.com/latex.php?latex=%5BQ%2CP%5D%3DQP-PQ&bg=ffffff&fg=000000&s=0) 。
注意,上述不互相對易關係僅適用於無限矩陣 (即量子力學的算符)。若
。
注意,上述不互相對易關係僅適用於無限矩陣 (即量子力學的算符)。若 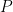 和
和 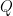 是
是 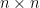 階有限矩陣,使用跡數循環不變性 (見“跡數的性質與應用”),
階有限矩陣,使用跡數循環不變性 (見“跡數的性質與應用”),
 ,
但
,
但  。在無限維空間,跡數未必定義完善,因為它不一定收斂。下面介紹的證法大致依循諾伊曼 (John von Neumann) 的推演方式[10]。第一個步驟設法創造一個引入交換子
。在無限維空間,跡數未必定義完善,因為它不一定收斂。下面介紹的證法大致依循諾伊曼 (John von Neumann) 的推演方式[10]。第一個步驟設法創造一個引入交換子 ![[Q,P] [Q,P]](https://s0.wp.com/latex.php?latex=%5BQ%2CP%5D&bg=ffffff&fg=000000&s=0) 的數學式。諾伊曼選擇了
的數學式。諾伊曼選擇了  。因為
。因為 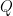 和
和 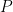 是 Hermitian 矩陣,
是 Hermitian 矩陣, ,
, ,可得
,可得
![\begin{aligned} (Q\mathbf{x})^{\ast}(P\mathbf{x})-(P\mathbf{x})^{\ast}(Q\mathbf{x})&=\mathbf{x}^{\ast}Q^{\ast}P\mathbf{x}-\mathbf{x}^{\ast}P^{\ast}Q\mathbf{x}\\ &=\mathbf{x}^\ast QP\mathbf{x}-\mathbf{x}^\ast PQ\mathbf{x}\\ &=\mathbf{x}^\ast(QP-PQ)\mathbf{x}\\ &=\mathbf{x}^\ast [Q,P]\mathbf{x}=\mathbf{x}^\ast i\hbar I\mathbf{x}\\ &=i\hbar\Vert\mathbf{x}\Vert^2=i\hbar, \end{aligned} \begin{aligned} (Q\mathbf{x})^{\ast}(P\mathbf{x})-(P\mathbf{x})^{\ast}(Q\mathbf{x})&=\mathbf{x}^{\ast}Q^{\ast}P\mathbf{x}-\mathbf{x}^{\ast}P^{\ast}Q\mathbf{x}\\ &=\mathbf{x}^\ast QP\mathbf{x}-\mathbf{x}^\ast PQ\mathbf{x}\\ &=\mathbf{x}^\ast(QP-PQ)\mathbf{x}\\ &=\mathbf{x}^\ast [Q,P]\mathbf{x}=\mathbf{x}^\ast i\hbar I\mathbf{x}\\ &=i\hbar\Vert\mathbf{x}\Vert^2=i\hbar, \end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D++%28Q%5Cmathbf%7Bx%7D%29%5E%7B%5Cast%7D%28P%5Cmathbf%7Bx%7D%29-%28P%5Cmathbf%7Bx%7D%29%5E%7B%5Cast%7D%28Q%5Cmathbf%7Bx%7D%29%26%3D%5Cmathbf%7Bx%7D%5E%7B%5Cast%7DQ%5E%7B%5Cast%7DP%5Cmathbf%7Bx%7D-%5Cmathbf%7Bx%7D%5E%7B%5Cast%7DP%5E%7B%5Cast%7DQ%5Cmathbf%7Bx%7D%5C%5C++%26%3D%5Cmathbf%7Bx%7D%5E%5Cast+QP%5Cmathbf%7Bx%7D-%5Cmathbf%7Bx%7D%5E%5Cast+PQ%5Cmathbf%7Bx%7D%5C%5C++%26%3D%5Cmathbf%7Bx%7D%5E%5Cast%28QP-PQ%29%5Cmathbf%7Bx%7D%5C%5C++%26%3D%5Cmathbf%7Bx%7D%5E%5Cast+%5BQ%2CP%5D%5Cmathbf%7Bx%7D%3D%5Cmathbf%7Bx%7D%5E%5Cast+i%5Chbar+I%5Cmathbf%7Bx%7D%5C%5C++%26%3Di%5Chbar%5CVert%5Cmathbf%7Bx%7D%5CVert%5E2%3Di%5Chbar%2C++%5Cend%7Baligned%7D&bg=ffffff&fg=000000&s=0) 其中最後一個等式係因量子態滿足歸一性
其中最後一個等式係因量子態滿足歸一性  。根據內積性質
。根據內積性質  (見“內積的定義”),我們可以得到另一個表達式:
(見“內積的定義”),我們可以得到另一個表達式:
 ,
其中
,
其中  代表複數
代表複數  的虛部。比較上面兩式,即有
的虛部。比較上面兩式,即有
 。
為了產生不確定性關係,下一個步驟必須引進不等式。複數的絕對值大於或等於它的虛部,即
。
為了產生不確定性關係,下一個步驟必須引進不等式。複數的絕對值大於或等於它的虛部,即  ,所以
,所以
 。
接著分離不等式裡面的
。
接著分離不等式裡面的 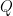 和
和 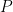 。使用 Schwarz 不等式 (見“Schwarz 不等式”)
。使用 Schwarz 不等式 (見“Schwarz 不等式”)
 可得
可得
 。
現在我們已經抵達整個推導過程的中途休息站,眼前的不等式是對易關係
。
現在我們已經抵達整個推導過程的中途休息站,眼前的不等式是對易關係 ![[Q,I]=i\hbar I [Q,I]=i\hbar I](https://s0.wp.com/latex.php?latex=%5BQ%2CI%5D%3Di%5Chbar+I&bg=ffffff&fg=000000&s=0) 的必然結果。海森堡不確定關係不等式與這個不等式有完全相同的形式,暗示我們剩下的工作不過就是將不確定性套入其中。
的必然結果。海森堡不確定關係不等式與這個不等式有完全相同的形式,暗示我們剩下的工作不過就是將不確定性套入其中。
定義一組新的位置矩陣和動量矩陣:
 ,
其中
,
其中  和
和  分別代表在量子態
分別代表在量子態  ,位置
,位置 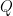 和動量
和動量 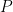 的期望值。明顯地,
的期望值。明顯地,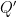 和
和  也是 Hermitian 矩陣。利用交換子運算法則 (見“交換子與可交換矩陣”):
也是 Hermitian 矩陣。利用交換子運算法則 (見“交換子與可交換矩陣”):
(1)![[A,I]=[I,A]=0 [A,I]=[I,A]=0](https://s0.wp.com/latex.php?latex=%5BA%2CI%5D%3D%5BI%2CA%5D%3D0&bg=ffffff&fg=000000&s=0)
(2)![\left[A+B,C+D\right]=[A,C]+[B,C]+[A,D]+[B,D] \left[A+B,C+D\right]=[A,C]+[B,C]+[A,D]+[B,D]](https://s0.wp.com/latex.php?latex=%5Cleft%5BA%2BB%2CC%2BD%5Cright%5D%3D%5BA%2CC%5D%2B%5BB%2CC%5D%2B%5BA%2CD%5D%2B%5BB%2CD%5D&bg=ffffff&fg=000000&s=0)
(3)![[kA,B]=[A,kB]=k[A,B] [kA,B]=[A,kB]=k[A,B]](https://s0.wp.com/latex.php?latex=%5BkA%2CB%5D%3D%5BA%2CkB%5D%3Dk%5BA%2CB%5D&bg=ffffff&fg=000000&s=0) ,
,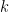 是一純量,
是一純量,
可導出
![\begin{aligned} \left[Q',P'\right]&=[Q-\left\langle Q\right\rangle I,P-\left\langle P\right\rangle I]\\ &=[Q,P]-\left\langle Q\right\rangle[I,P]-\left\langle P\right\rangle[Q,I]+\left\langle Q\right\rangle\left\langle P\right\rangle[I,I]\\ &=[Q,P]=i\hbar.\end{aligned} \begin{aligned} \left[Q',P'\right]&=[Q-\left\langle Q\right\rangle I,P-\left\langle P\right\rangle I]\\ &=[Q,P]-\left\langle Q\right\rangle[I,P]-\left\langle P\right\rangle[Q,I]+\left\langle Q\right\rangle\left\langle P\right\rangle[I,I]\\ &=[Q,P]=i\hbar.\end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D++%5Cleft%5BQ%27%2CP%27%5Cright%5D%26%3D%5BQ-%5Cleft%5Clangle+Q%5Cright%5Crangle+I%2CP-%5Cleft%5Clangle+P%5Cright%5Crangle+I%5D%5C%5C++%26%3D%5BQ%2CP%5D-%5Cleft%5Clangle+Q%5Cright%5Crangle%5BI%2CP%5D-%5Cleft%5Clangle+P%5Cright%5Crangle%5BQ%2CI%5D%2B%5Cleft%5Clangle+Q%5Cright%5Crangle%5Cleft%5Clangle+P%5Cright%5Crangle%5BI%2CI%5D%5C%5C++%26%3D%5BQ%2CP%5D%3Di%5Chbar.%5Cend%7Baligned%7D&bg=ffffff&fg=000000&s=0) 我們發現
我們發現 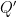 和
和  也遵守對易關係,以
也遵守對易關係,以 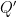 取代
取代 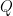 ,
, 取代
取代 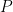 ,即得
,即得
 。
這個不等式其實就是不確定性原理。何以如此?利用
。
這個不等式其實就是不確定性原理。何以如此?利用 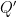 ,
, 和
和  的定義,
的定義,
 同樣地,
同樣地, 。所以,
。所以,
 。
。
從以上推導我們知道不確定性原理並非源自實驗儀器的測量誤差,而是粒子內稟的量子性質,即位置與動量不互相對易關係。最後我引用維基百科關於不確定性原理「名稱」的一段論述當作本文的結語[1]:
註解:
[1] 維基百科:不確定性原理,見「名稱」一節。
[2] 普朗克常數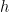 是量子力學的註冊商標,出現在普朗克關係式
是量子力學的註冊商標,出現在普朗克關係式  ,其中
,其中 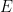 是粒子的能量,
是粒子的能量, 是電磁波的頻率。普朗克常數與光速
是電磁波的頻率。普朗克常數與光速  和萬有引力常數
和萬有引力常數 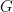 並稱為大自然的三個基本常數。詳見維基百科:普朗克常數。
並稱為大自然的三個基本常數。詳見維基百科:普朗克常數。
[3] 關於海森堡 (Werner Heisenberg) 的生平介紹請見維基百科:維爾納‧海森堡。
[4] 維基百科:不確定性原理,見「歷史」一節。
[5] 費曼 (Richard P. Feynman) 著 Essentials of Physics Explained by Its Most Brilliant Teacher,中譯本《費曼的六堂Easy物理課》,師明睿譯,天下文化出版,2001年,頁153-155。
[6] 愛因斯坦對海森堡說的英譯文是:“It is the theory which decides what can be observed.” 見談測不準原理的起始,原標題是 Remarks on the Origin of the Relations of Uncertainty。
[7] 矩陣力學 (matrix mechanics) 是量子力學的一種表述形式,由海森堡、玻恩 (Max Born) 和約當 (Pascual Jordan) 於1925年提出。矩陣力學假設 (1) 所有的可觀察物理量都可以用 Hermitian 矩陣表示,(2) 一個物理量的觀察值是該矩陣的特徵值,(3) 一個物理系統的位置矩陣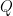 與動量矩陣
與動量矩陣 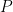 滿足對易關係:
滿足對易關係: 。對易關係無法從古典物理推導出來,它是一個全新的假定,只有實驗才能確認它的真實性。見維基百科:矩陣力學。
。對易關係無法從古典物理推導出來,它是一個全新的假定,只有實驗才能確認它的真實性。見維基百科:矩陣力學。
[8] 量子態 (quantum state) 描述量子系統的狀態。在量子系統裏,量子態由所有可觀察量的機率分布所定義。見維基百科:量子態。
[9] 機率幅 (probability amplitude) 是一個描述粒子的量子行為的複函數。當描述粒子的位置時,機率幅是一個波函數,表達為位置的函數。在量子力學中,機率幅常用 表示,
表示, 則代表機率幅的機率密度函數。見維基百科:機率幅。
則代表機率幅的機率密度函數。見維基百科:機率幅。
[10] 諾伊曼 (John von Neumann) 所著 Mathematical Foundations of Quantum Mechanics,1949年出版,頁233-235。
在量子力學裏,不確定性原理[1](uncertainty principle) 表明:粒子的位置與動量不可同時被確定,位置的不確定性

Werner Heisenberg (1901-1976) From http://www.robertphoenix.com/content/wp-content/uploads/2012/11/Werner_Heisenberg_14.jpeg
物理學家費曼 (Richard P. Feynman) 說[5]:
量子力學所描述的,概括一切物質行為的細節,尤其對那些發生在原子尺度的部分特別管用。非常微小東西的行為,跟我們的直接經驗完全不同,它們的行為既非波動性質,亦非粒子性質。也不完全像雲、撞球檯上的球、或彈簧上的砝碼。總而言之,完全不像我們日常看見過的任何東西。隨後又補充解釋:
因為所有人生經歷、思維直覺,無不是從大尺度事物來的。我們的經驗會隨時提醒我們,大尺度事物會如何因應,但是微小尺度的事物所採取的因應方式迥然不同。所以我們學習它的時候,必須強迫自己用抽象或想像的方式,而絕不能到我們直接經驗中去尋找聯想。
既然我們無法從直接經驗去尋找聯想量子世界的運行方式,物理學家選擇何種假設或模型,在很大的程度上取決於個人的想像力與信念。1925年海森堡思考著量子力學的建立基礎,他憶起愛因斯坦曾說[6]:「你的理論決定了你所觀察到的。」這句話啟發他換一個角度看待問題,之後他建議[4]:只有在實驗裏能夠測量到的物理量,稱為可觀察量 (observable),才可以用理論描述其物理行為。當然,並不是所有的物理學家都抱持相同的看法。量子力學的另一位創建者薛丁格 (Erwin Schrödinger) 起初也不認同海森堡的想法 (但很快地,薛丁格於1926年證明波力學與矩陣力學是量子力學的兩種等價描述[6])。儘管未獲得眾多同行的支持,海森堡、玻恩 (Max Born) 與約當 (Pascual Jordan) 仍於1925年共同創立矩陣力學[7](matrix mechanics),大膽假設關於運動的古典概念不適用於量子層級。在原子裏的電子並不是運動於明確的軌道,而是模糊不清,無法觀察到的軌域。海森堡棄絕任何涉及粒子運動軌道的詳細計算,因為運動軌道是無法直接觀察到的。他選擇另一條道路:專注於研究電子躍遷時,所發射的光的離散頻率和強度。他計算出代表位置和動量的無限矩陣,這些矩陣能夠正確地預測電子躍遷所發射出光波的強度[4]。
海森堡從電子轉移的現象歸納出矩陣力學的前提[7]:所有的可觀察物理量都可以用矩陣表示。矩陣的特徵值集合是該物理量可能出現的觀察值。對一般人來說,這絕對是一個聞所未聞的神秘主義。在經驗世界裏,我們頂多用一個隨機變數來表示可觀察量,譬如,投擲骰子可能出現的點數,可是觀察量本身怎麼會跟矩陣扯上關係?況且在工程科學中,矩陣不都是拿來表示線性系統嗎?但量子力學不同於過去的典範,物理學家總是各憑本事編造出許多奇怪的想法企圖描繪原子層次的行為。不論信與不信,我們暫且接受這個瘋狂的假設。因為實驗測量的結果是實數,Hermitian 矩陣的特徵值又都是實數 (
為了弄清楚海森堡的想法,我們必須知道 Hermitian 矩陣的一些基本性質。在一量子系統中,令
1925年,玻恩閱讀了海森堡的論文後,發現位置與動量無限矩陣有一個很顯著的關係──它們不可交換 (或說不互相對易)[4,7]。不確定性原理是下列不互相對易關係的直接結果:
定義一組新的位置矩陣和動量矩陣:
(1)
(2)
(3)
可導出
從以上推導我們知道不確定性原理並非源自實驗儀器的測量誤差,而是粒子內稟的量子性質,即位置與動量不互相對易關係。最後我引用維基百科關於不確定性原理「名稱」的一段論述當作本文的結語[1]:
有很久一段時間,不確定性原理被稱為「測不準原理」,但事實上,不確定性原理是類波系統內秉的性質,與測量準確不準確並沒有關係 (請查閱本條目稍後觀察者效應一節),因此,該譯名並未正確表達出這原理的內涵。另外,英語稱此原理為「Uncertainty Principle」,直譯為「不確定性原理」,並沒有「測不準原理」這種說法,其他語言與英語的情況類似,除中文外,並無「測不準原理」一詞。現今,在中國大陸的教科書中,該原理的正式譯名也已改為「不确定性原理」。
註解:
[1] 維基百科:不確定性原理,見「名稱」一節。
[2] 普朗克常數
[3] 關於海森堡 (Werner Heisenberg) 的生平介紹請見維基百科:維爾納‧海森堡。
[4] 維基百科:不確定性原理,見「歷史」一節。
[5] 費曼 (Richard P. Feynman) 著 Essentials of Physics Explained by Its Most Brilliant Teacher,中譯本《費曼的六堂Easy物理課》,師明睿譯,天下文化出版,2001年,頁153-155。
[6] 愛因斯坦對海森堡說的英譯文是:“It is the theory which decides what can be observed.” 見談測不準原理的起始,原標題是 Remarks on the Origin of the Relations of Uncertainty。
[7] 矩陣力學 (matrix mechanics) 是量子力學的一種表述形式,由海森堡、玻恩 (Max Born) 和約當 (Pascual Jordan) 於1925年提出。矩陣力學假設 (1) 所有的可觀察物理量都可以用 Hermitian 矩陣表示,(2) 一個物理量的觀察值是該矩陣的特徵值,(3) 一個物理系統的位置矩陣
[8] 量子態 (quantum state) 描述量子系統的狀態。在量子系統裏,量子態由所有可觀察量的機率分布所定義。見維基百科:量子態。
[9] 機率幅 (probability amplitude) 是一個描述粒子的量子行為的複函數。當描述粒子的位置時,機率幅是一個波函數,表達為位置的函數。在量子力學中,機率幅常用
[10] 諾伊曼 (John von Neumann) 所著 Mathematical Foundations of Quantum Mechanics,1949年出版,頁233-235。
No comments:
Post a Comment