phymath999: 把调和场看作一个给定区域内的静电场，区域内没有静电荷（否则就不是调和场了）。我们断言电势极值不能在区域内取到。以极大值为例，如果存在一点是电势极大值，那么在这一点附近电场都是离开该点方向的。在这一点附近取一个Gauss面S，根据Gauss定理可知S内必然存在正电荷，与区域内没有静电荷的假设相违背

Thursday, February 12, 2015

把调和场看作一个给定区域内的静电场，区域内没有静电荷（否则就不是调和场了）。我们断言电势极值不能在区域内取到。以极大值为例，如果存在一点是电势极大值，那么在这一点附近电场都是离开该点方向的。在这一点附近取一个Gauss面S，根据Gauss定理可知S内必然存在正电荷，与区域内没有静电荷的假设相违背

调和函数在什么条件下在全区域内为0？欢迎both物理and数学上的解释

从一个线性表面波速度势函数的结论中看到的。

添加评论

按投票排序按时间排序

6 个回答

知乎用户

收起

知乎用户、德安城、刘权庆等人赞同

如果是题主是在物理遇到的问题，那么想要得到的结论应该是这样的：如果调和函数在边界上取值为零，则在整个区域内处处为零。

数学上解释，这实际上是复变函数的一个结果：最大模原理，我个人理解这是解析函数平均值定理的一个推论，可以在任何一本复变函数或是复分析的教材中找到证明。当然这一结论的证明也可以不依赖于复变函数。利用微积分的知识也可以证明这一结论。基本思想也是先利用Gauss公式证明平均值定理，题主可以参考相关的教科书。

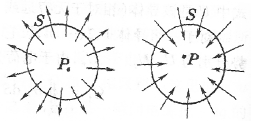
物理上解释，这里可以提供一种看法。把调和场看作一个给定区域内的静电场，区域内没有静电荷（否则就不是调和场了）。我们断言电势极值不能在区域内取到。以极大值为例，如果存在一点是电势极大值，那么在这一点附近电场都是离开该点方向的。在这一点附近取一个Gauss面 $S$ ，根据Gauss定理可知 $S$ 内必然存在正电荷，与区域内没有静电荷的假设相违背。

另外binjie li指出无源的稳态热传导方程也会退化为Laplace方程，因此调和函数也对应一个稳态且区域内部没有热源的温度分布。从物理上看，似乎比较显然显然在区域内部不可能达到极值。所在边界上取值都为零，那么在区域内部显然也应为零。

当然，有几位同学的答案“如果调和函数在很小的区域内恒为0，它必在整个区域上恒为0”结论也是对的，但这实际上不是调和函数特有的性质而是一般解析函数所具有的性质。而且在物理上这个结论似乎也并不重要，只是偶尔出现在唯一性定理的证明中。

编辑于 2014-08-07 4 条评论感谢分享收藏 • 没有帮助 •

余翔

收起

你可以看一下《数学物理方程》第二版（谷超豪）书上有与这个问题相关的内容（图片都是来自这本书的）
1.首先证明调和函数关于自变量的解析函数
2.如果调和函数在很小的区域内恒为0，那么它必在整个区域上恒为0，这个我还没有想到严格的证明，不过你这个结论是正确的。
可以回答你的问题部分
调和函数在全区域内为0的充分条件是：调和函数在很小的区域内恒为0。是否为充要条件还要证明‘
update
如果调和函数 $u$ 在边界上恒为0，那么它在区域内也只能恒为0，证明如下
考虑区域 $\Omega 内$ 的调和函数 $u$ ，它在 $\Omega$ 的边界 $\Gamma$ 上恒为0
$\nabla^{2}u=0$ （在 $\Omega$ 中）
$u|_{\Gamma}=0$
可以看出 $u=0$ 是方程的解，在根据调和函数Dirichlet问题解的唯一性可知， $u=0$ 是方程的唯一解，所以 $u$ 在区域内只能为0

参考
[1].数学物理方程