李淼的博客
http://motls.blogspot.com/2010/01/erik-verlinde-comments-about-entropic.html
http://limiao.blog.caixin.com
新熵力图像
从上学期开始,我一直想用引力即熵力理论找到暗能量的具体形式(当然私心是找到支持全息暗能量的证据),我们没有成功,似乎没有任何人成功了。
一开始,我就觉得Verlinde的想法中闭合的全息屏是最大的障碍,因为要研究宇宙学,不存在任何整体的Killing 矢量,特别是某种宇宙学视界上不存在整体Killing矢量,所以他的想法很难用到宇宙学上。
所以,我想到研究一个任意小的、开放的holographic screen。一个开放的全息屏当然不包含任何空间和物质,所以无法直接研究能量,但可以研究某段时间流过屏的能量。我们摸索了很长时间,后来我建议苗荣欣同学将Jacobson的原始做法移植到一个time-like全息屏上。
从7月份一直折腾到上个月,我们似乎看到了希望。开学后,谷伟也加入了我们。昨天,我将最后结果贴出来了:
A New Entropic Force Scenario and Holographic Thermodynamics
这个project一共做了四个月左右,终于结束了。
昨天在南宁的The first international workshop on the LHC era physics (LHEP2010) 上,我已经做了这个工作的演讲。
如果用一句话总结我们的建议与Verlinde的不同,就是,我们建议用Brown-York能量做全息屏上的能量,而不是Tolman-Komar质量,Verlinde假设后者满足能量均分定理(通过爱因斯坦方程,这个假设是正确的),而Brown-York能量一般不满足能量均分。
更一般的,我们从屏上的surface stress tensor出发。这个surface stress tensor含有面能量密度以及面压强信息,所以,我们还多了一个数据,就是压强。这个面stress tensor正比于面在时空中的extrinsic curvature。在Verlinde的图像中,面上只有温度,温度也是由几何给出的。我们的建议虽然不同,但在用到几何上面,与Verlinde并无本质不同。
我们建议的能量有如下的形式:
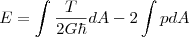
我们看到,非零的面压强破坏了能量均分。
推导爱因斯坦方程的大致过程是,从能量出发
![]()
这个能流发生在时空中,根据全息原理,应该等于屏上的能量变化,而屏上的能量变化分两部分,一部分是面密度的变化,另一部分是能量从屏流到屏的其他部分,具体公式就不写了,图示如下:
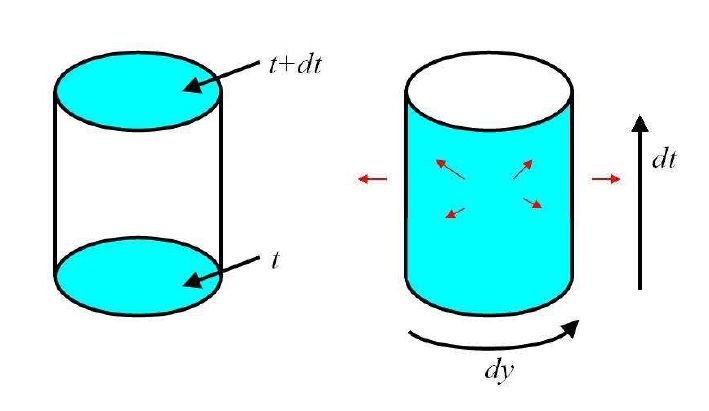
将两个能量变化相等,就能推出爱因斯坦方程。我们的推导比Verlinde的推导“完美”。第一,开放的屏可以任意小,所以积分方程可以变成微分方程。第二,Verlinde需要温度,而对于任意封闭的面,温度不是恒正定的。第三,既然我们需要用到面上的stress tensor而不是温度,我们可以用别的量取代extrinsic curvature,从而获得其他理论如高阶导数理论。过去我和庞毅证明了,Verlinde理论不能用到高导数理论。
我们的推导与Jacobson相似,他也用了能流,但他的全息屏是类光的,我们的是类时的。他只用到类光屏的面积变化(即熵变化),我们没有引进热力学。但后来我们可以引进热力学,采用Verlinde温度,但熵不由几何直接给出,需要解热力学第一定律。换言之,我们对爱因斯坦方程的推导还不能看成是热力学第一定律的应用。另外,类光屏上压强为零,也没有能量从屏流到屏的另一部分现象(所以热力学很简单,任意小的开放类光屏类似一个封闭系统)。
热力学需要单独研究,引进Verlinde温度,以及面压强,甚至化学势(事后看,这是自然的,面的变化自然会导致被激发的自由度的变化),我们研究了一个球对称气体,获得了全息熵。这个全息熵很像Bekenstein熵界,但对于不同的气体具体数值不同。全息熵远远大于气体的统计熵,说明全息屏上带有更多的信息。虽然我们的全息熵公式里有一个未定常数,这个结果是我们的图像的预言,而Verlinde图像还没有预言。
气体全息熵的导出是我相信这个新建议的主要原因。
全息熵中的未定常数是我们下一步的研究目标。我们现在同时在做三个相关的研究计划。
另外,很重要的是,Verlinde图像无法用到热力学上,对于一个气体,很难获得可以接受的熵公式。
我建议大家读我们的文章。
当然,不用说,还有很多要做的研究。
惯性是头倔驴
一开始,我就觉得Verlinde的想法中闭合的全息屏是最大的障碍,因为要研究宇宙学,不存在任何整体的Killing 矢量,特别是某种宇宙学视界上不存在整体Killing矢量,所以他的想法很难用到宇宙学上。
所以,我想到研究一个任意小的、开放的holographic screen。一个开放的全息屏当然不包含任何空间和物质,所以无法直接研究能量,但可以研究某段时间流过屏的能量。我们摸索了很长时间,后来我建议苗荣欣同学将Jacobson的原始做法移植到一个time-like全息屏上。
从7月份一直折腾到上个月,我们似乎看到了希望。开学后,谷伟也加入了我们。昨天,我将最后结果贴出来了:
A New Entropic Force Scenario and Holographic Thermodynamics
这个project一共做了四个月左右,终于结束了。
昨天在南宁的The first international workshop on the LHC era physics (LHEP2010) 上,我已经做了这个工作的演讲。
如果用一句话总结我们的建议与Verlinde的不同,就是,我们建议用Brown-York能量做全息屏上的能量,而不是Tolman-Komar质量,Verlinde假设后者满足能量均分定理(通过爱因斯坦方程,这个假设是正确的),而Brown-York能量一般不满足能量均分。
更一般的,我们从屏上的surface stress tensor出发。这个surface stress tensor含有面能量密度以及面压强信息,所以,我们还多了一个数据,就是压强。这个面stress tensor正比于面在时空中的extrinsic curvature。在Verlinde的图像中,面上只有温度,温度也是由几何给出的。我们的建议虽然不同,但在用到几何上面,与Verlinde并无本质不同。
我们建议的能量有如下的形式:
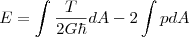
我们看到,非零的面压强破坏了能量均分。
推导爱因斯坦方程的大致过程是,从能量出发

这个能流发生在时空中,根据全息原理,应该等于屏上的能量变化,而屏上的能量变化分两部分,一部分是面密度的变化,另一部分是能量从屏流到屏的其他部分,具体公式就不写了,图示如下:

将两个能量变化相等,就能推出爱因斯坦方程。我们的推导比Verlinde的推导“完美”。第一,开放的屏可以任意小,所以积分方程可以变成微分方程。第二,Verlinde需要温度,而对于任意封闭的面,温度不是恒正定的。第三,既然我们需要用到面上的stress tensor而不是温度,我们可以用别的量取代extrinsic curvature,从而获得其他理论如高阶导数理论。过去我和庞毅证明了,Verlinde理论不能用到高导数理论。
我们的推导与Jacobson相似,他也用了能流,但他的全息屏是类光的,我们的是类时的。他只用到类光屏的面积变化(即熵变化),我们没有引进热力学。但后来我们可以引进热力学,采用Verlinde温度,但熵不由几何直接给出,需要解热力学第一定律。换言之,我们对爱因斯坦方程的推导还不能看成是热力学第一定律的应用。另外,类光屏上压强为零,也没有能量从屏流到屏的另一部分现象(所以热力学很简单,任意小的开放类光屏类似一个封闭系统)。
热力学需要单独研究,引进Verlinde温度,以及面压强,甚至化学势(事后看,这是自然的,面的变化自然会导致被激发的自由度的变化),我们研究了一个球对称气体,获得了全息熵。这个全息熵很像Bekenstein熵界,但对于不同的气体具体数值不同。全息熵远远大于气体的统计熵,说明全息屏上带有更多的信息。虽然我们的全息熵公式里有一个未定常数,这个结果是我们的图像的预言,而Verlinde图像还没有预言。
气体全息熵的导出是我相信这个新建议的主要原因。
全息熵中的未定常数是我们下一步的研究目标。我们现在同时在做三个相关的研究计划。
另外,很重要的是,Verlinde图像无法用到热力学上,对于一个气体,很难获得可以接受的熵公式。
我建议大家读我们的文章。
当然,不用说,还有很多要做的研究。
惯性是头倔驴
||
物体具有保持自己运动状态不变的性质,我们把这一性质叫做惯性。惯性的大小只跟物体的质量有关系,是物体的固有属性。
为了说明固有属性是个啥玩意儿,我们讲一个月亮驴子的故事吧。月亮在绕着地球转动,像一头驴子在绕着磨盘转动,所以我们叫他月亮驴子。显然,做圆周运动的月亮驴子,其运动方向在不断的变化,也就是说其运动状态在不断的变化。能改变物体运动状态的一定是力。地球对月亮驴子的引力像牵着驴子的缰绳一样改变着月亮驴子的运动状态。
虽然月亮驴子不得不服从于缰绳的意志,但是这不是月亮驴子的本性。即使是这个时候,月亮驴子的本性也是不变的,他有做匀速直线运动的欲望。可见,惯性就是倔驴的“倔脾气”,跟外力没有关系。一旦缰绳没有了,所有的力都撤销,或者抵消,月亮驴子必将显露出其本身固有的属性,做匀速直线运动或者静止,这就是牛顿第一定律。
根据等效原理,如果我们定义“自由落体惯性系”,那么我们就可以不把引力看成是力,而是几何。也就是说,所有关于引力的信息都可以用时空的弯曲来描述。时空可以对应在一张全息屏上,这大概就是全息原理吧
熵力,逗你玩
为了说明固有属性是个啥玩意儿,我们讲一个月亮驴子的故事吧。月亮在绕着地球转动,像一头驴子在绕着磨盘转动,所以我们叫他月亮驴子。显然,做圆周运动的月亮驴子,其运动方向在不断的变化,也就是说其运动状态在不断的变化。能改变物体运动状态的一定是力。地球对月亮驴子的引力像牵着驴子的缰绳一样改变着月亮驴子的运动状态。
虽然月亮驴子不得不服从于缰绳的意志,但是这不是月亮驴子的本性。即使是这个时候,月亮驴子的本性也是不变的,他有做匀速直线运动的欲望。可见,惯性就是倔驴的“倔脾气”,跟外力没有关系。一旦缰绳没有了,所有的力都撤销,或者抵消,月亮驴子必将显露出其本身固有的属性,做匀速直线运动或者静止,这就是牛顿第一定律。
根据等效原理,如果我们定义“自由落体惯性系”,那么我们就可以不把引力看成是力,而是几何。也就是说,所有关于引力的信息都可以用时空的弯曲来描述。时空可以对应在一张全息屏上,这大概就是全息原理吧
熵力,逗你玩
||
料想Erik Verlinder看不懂中文,所以将题目写的好玩一点吧。事实上,博主根本没有资格评论Erik Verlinder同学的文章。这篇文章在10年和11年红的发紫,尤其在中国。我这人反应慢在大学同学里是出了名的。这里有一段小故事就不必讲了。总而言之,当时没兴趣,现在有兴趣了,找出来研究一把。
Erik Verlinder同学的文章严谨但不古板,最后还以大家喜闻乐见的方式结尾,皆大欢喜。内行看门道,外行看热闹,所以很多人喜欢看热闹,这个Erik Verlinder同学是知道的。热闹是什么?最热闹的事情莫过于打架。大街上如果有人打架,立马会围过来一圈人。当然有拉架的,有煽风点火的,更多的是看热闹的。如果你问他,您干什么的?答案是:"打酱油的!"文章的结尾提到牛顿和胡克打架。据说和牛顿打架的人很多,我想大概是因为牛顿自恃武功天下第一,横行乡里,引起很多人不服,前来挑战。Erik Verlinder同学最后一句话有点“数风流人物,还看今朝”的意思,可谓是霸气外漏。
熵力的基本假设是全息原理和等效原理,其中等效原理在这篇博文里讲的很详细,而全息原理俺不懂,想当然的以为就跟全息照相类似吧(亲爱的读者,您觉得呢?)。根据等效原理,如果我们定义“自由落体惯性系”,那么我们就可以不把引力看成是力,而是几何。也就是说,所有关于引力的信息都可以用时空的弯曲来描述。时空可以对应在一张全息屏上,这大概就是全息原理吧。过几天有空研究研究这个事情,亲爱的读者您如果知道,望不吝赐教。全息屏上可以定义熵,熵的变化描述时空的变化,而时空的变化描述引力,所以熵可以描述引力。Erik Verlinder做的事情是将这其中的曲折展示给大家看,推导出牛顿的引力公式和爱因斯坦方程。这里科普下,该文研究的是引力,说引力可以用熵来描写,没有其他三种作用力什么事儿。亲爱的读者,您可别把他们牵扯进来,以防打架。比如说摩擦力是电磁力,跟熵力不搭嘎。如果您是中学生,那您必然很熟悉胡克定律。一提到胡克,您脑海中就浮现出一根弹簧,胡克说弹力和其伸长量成正比。这里有一点小小的误会,您所想的那个弹力也是电磁力,别牵扯进来。
个人觉得熵力靠谱(不是不评论吗?)。孤立系熵不减,而引力没有排斥力,二者本应该有渊源。还有一个非常重要物理量也是单向变化的,您知道她是谁吗?这里您能得到什么启示?

这是什么车?
http://blog.sciencenet.cn/blog-441981-770672.html
Erik Verlinder同学的文章严谨但不古板,最后还以大家喜闻乐见的方式结尾,皆大欢喜。内行看门道,外行看热闹,所以很多人喜欢看热闹,这个Erik Verlinder同学是知道的。热闹是什么?最热闹的事情莫过于打架。大街上如果有人打架,立马会围过来一圈人。当然有拉架的,有煽风点火的,更多的是看热闹的。如果你问他,您干什么的?答案是:"打酱油的!"文章的结尾提到牛顿和胡克打架。据说和牛顿打架的人很多,我想大概是因为牛顿自恃武功天下第一,横行乡里,引起很多人不服,前来挑战。Erik Verlinder同学最后一句话有点“数风流人物,还看今朝”的意思,可谓是霸气外漏。
熵力的基本假设是全息原理和等效原理,其中等效原理在这篇博文里讲的很详细,而全息原理俺不懂,想当然的以为就跟全息照相类似吧(亲爱的读者,您觉得呢?)。根据等效原理,如果我们定义“自由落体惯性系”,那么我们就可以不把引力看成是力,而是几何。也就是说,所有关于引力的信息都可以用时空的弯曲来描述。时空可以对应在一张全息屏上,这大概就是全息原理吧。过几天有空研究研究这个事情,亲爱的读者您如果知道,望不吝赐教。全息屏上可以定义熵,熵的变化描述时空的变化,而时空的变化描述引力,所以熵可以描述引力。Erik Verlinder做的事情是将这其中的曲折展示给大家看,推导出牛顿的引力公式和爱因斯坦方程。这里科普下,该文研究的是引力,说引力可以用熵来描写,没有其他三种作用力什么事儿。亲爱的读者,您可别把他们牵扯进来,以防打架。比如说摩擦力是电磁力,跟熵力不搭嘎。如果您是中学生,那您必然很熟悉胡克定律。一提到胡克,您脑海中就浮现出一根弹簧,胡克说弹力和其伸长量成正比。这里有一点小小的误会,您所想的那个弹力也是电磁力,别牵扯进来。
个人觉得熵力靠谱(不是不评论吗?)。孤立系熵不减,而引力没有排斥力,二者本应该有渊源。还有一个非常重要物理量也是单向变化的,您知道她是谁吗?这里您能得到什么启示?

这是什么车?
http://blog.sciencenet.cn/blog-441981-770672.html
新熵力图像
从上学期开始,我一直想用引力即熵力理论找到暗能量的具体形式(当然私心是找到支持全息暗能量的证据),我们没有成功,似乎没有任何人成功了。
一开始,我就觉得Verlinde的想法中闭合的全息屏是最大的障碍,因为要研究宇宙学,不存在任何整体的Killing 矢量,特别是某种宇宙学视界上不存在整体Killing矢量,所以他的想法很难用到宇宙学上。
所以,我想到研究一个任意小的、开放的holographic screen。一个开放的全息屏当然不包含任何空间和物质,所以无法直接研究能量,但可以研究某段时间流过屏的能量。我们摸索了很长时间,后来我建议苗荣欣同学将Jacobson的原始做法移植到一个time-like全息屏上。
从7月份一直折腾到上个月,我们似乎看到了希望。开学后,谷伟也加入了我们。昨天,我将最后结果贴出来了:
A New Entropic Force Scenario and Holographic Thermodynamics
这个project一共做了四个月左右,终于结束了。
昨天在南宁的The first international workshop on the LHC era physics (LHEP2010) 上,我已经做了这个工作的演讲。
如果用一句话总结我们的建议与Verlinde的不同,就是,我们建议用Brown-York能量做全息屏上的能量,而不是Tolman-Komar质量,Verlinde假设后者满足能量均分定理(通过爱因斯坦方程,这个假设是正确的),而Brown-York能量一般不满足能量均分。
更一般的,我们从屏上的surface stress tensor出发。这个surface stress tensor含有面能量密度以及面压强信息,所以,我们还多了一个数据,就是压强。这个面stress tensor正比于面在时空中的extrinsic curvature。在Verlinde的图像中,面上只有温度,温度也是由几何给出的。我们的建议虽然不同,但在用到几何上面,与Verlinde并无本质不同。
我们建议的能量有如下的形式:
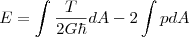
我们看到,非零的面压强破坏了能量均分。
推导爱因斯坦方程的大致过程是,从能量出发
![]()

这个能流发生在时空中,根据全息原理,应该等于屏上的能量变化,而屏上的能量变化分两部分,一部分是面密度的变化,另一部分是能量从屏流到屏的其他部分,具体公式就不写了,图示如下:

将两个能量变化相等,就能推出爱因斯坦方程。我们的推导比Verlinde的推导“完美”。第一,开放的屏可以任意小,所以积分方程可以变成微分方程。第二,Verlinde需要温度,而对于任意封闭的面,温度不是恒正定的。第三,既然我们需要用到面上的stress tensor而不是温度,我们可以用别的量取代extrinsic curvature,从而获得其他理论如高阶导数理论。过去我和庞毅证明了,Verlinde理论不能用到高导数理论。
我们的推导与Jacobson相似,他也用了能流,但他的全息屏是类光的,我们的是类时的。他只用到类光屏的面积变化(即熵变化),我们没有引进热力学。但后来我们可以引进热力学,采用Verlinde温度,但熵不由几何直接给出,需要解热力学第一定律。换言之,我们对爱因斯坦方程的推导还不能看成是热力学第一定律的应用。另外,类光屏上压强为零,也没有能量从屏流到屏的另一部分现象(所以热力学很简单,任意小的开放类光屏类似一个封闭系统)。
热力学需要单独研究,引进Verlinde温度,以及面压强,甚至化学势(事后看,这是自然的,面的变化自然会导致被激发的自由度的变化),我们研究了一个球对称气体,获得了全息熵。这个全息熵很像Bekenstein熵界,但对于不同的气体具体数值不同。全息熵远远大于气体的统计熵,说明全息屏上带有更多的信息。虽然我们的全息熵公式里有一个未定常数,这个结果是我们的图像的预言,而Verlinde图像还没有预言。
气体全息熵的导出是我相信这个新建议的主要原因。
全息熵中的未定常数是我们下一步的研究目标。我们现在同时在做三个相关的研究计划。
另外,很重要的是,Verlinde图像无法用到热力学上,对于一个气体,很难获得可以接受的熵公式。
我建议大家读我们的文章。
当然,不用说,还有很多要做的研究。
Temperature is defined as the conjugate variable to energy
The force is entirely a consequence of the amount of configuration space and not mediated by anything. There is no space yet.
Erik Verlinde: comments about the entropic force of gravity
一开始,我就觉得Verlinde的想法中闭合的全息屏是最大的障碍,因为要研究宇宙学,不存在任何整体的Killing 矢量,特别是某种宇宙学视界上不存在整体Killing矢量,所以他的想法很难用到宇宙学上。
所以,我想到研究一个任意小的、开放的holographic screen。一个开放的全息屏当然不包含任何空间和物质,所以无法直接研究能量,但可以研究某段时间流过屏的能量。我们摸索了很长时间,后来我建议苗荣欣同学将Jacobson的原始做法移植到一个time-like全息屏上。
从7月份一直折腾到上个月,我们似乎看到了希望。开学后,谷伟也加入了我们。昨天,我将最后结果贴出来了:
A New Entropic Force Scenario and Holographic Thermodynamics
这个project一共做了四个月左右,终于结束了。
昨天在南宁的The first international workshop on the LHC era physics (LHEP2010) 上,我已经做了这个工作的演讲。
如果用一句话总结我们的建议与Verlinde的不同,就是,我们建议用Brown-York能量做全息屏上的能量,而不是Tolman-Komar质量,Verlinde假设后者满足能量均分定理(通过爱因斯坦方程,这个假设是正确的),而Brown-York能量一般不满足能量均分。
更一般的,我们从屏上的surface stress tensor出发。这个surface stress tensor含有面能量密度以及面压强信息,所以,我们还多了一个数据,就是压强。这个面stress tensor正比于面在时空中的extrinsic curvature。在Verlinde的图像中,面上只有温度,温度也是由几何给出的。我们的建议虽然不同,但在用到几何上面,与Verlinde并无本质不同。
我们建议的能量有如下的形式:
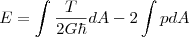
我们看到,非零的面压强破坏了能量均分。
推导爱因斯坦方程的大致过程是,从能量出发

这个能流发生在时空中,根据全息原理,应该等于屏上的能量变化,而屏上的能量变化分两部分,一部分是面密度的变化,另一部分是能量从屏流到屏的其他部分,具体公式就不写了,图示如下:

将两个能量变化相等,就能推出爱因斯坦方程。我们的推导比Verlinde的推导“完美”。第一,开放的屏可以任意小,所以积分方程可以变成微分方程。第二,Verlinde需要温度,而对于任意封闭的面,温度不是恒正定的。第三,既然我们需要用到面上的stress tensor而不是温度,我们可以用别的量取代extrinsic curvature,从而获得其他理论如高阶导数理论。过去我和庞毅证明了,Verlinde理论不能用到高导数理论。
我们的推导与Jacobson相似,他也用了能流,但他的全息屏是类光的,我们的是类时的。他只用到类光屏的面积变化(即熵变化),我们没有引进热力学。但后来我们可以引进热力学,采用Verlinde温度,但熵不由几何直接给出,需要解热力学第一定律。换言之,我们对爱因斯坦方程的推导还不能看成是热力学第一定律的应用。另外,类光屏上压强为零,也没有能量从屏流到屏的另一部分现象(所以热力学很简单,任意小的开放类光屏类似一个封闭系统)。
热力学需要单独研究,引进Verlinde温度,以及面压强,甚至化学势(事后看,这是自然的,面的变化自然会导致被激发的自由度的变化),我们研究了一个球对称气体,获得了全息熵。这个全息熵很像Bekenstein熵界,但对于不同的气体具体数值不同。全息熵远远大于气体的统计熵,说明全息屏上带有更多的信息。虽然我们的全息熵公式里有一个未定常数,这个结果是我们的图像的预言,而Verlinde图像还没有预言。
气体全息熵的导出是我相信这个新建议的主要原因。
全息熵中的未定常数是我们下一步的研究目标。我们现在同时在做三个相关的研究计划。
另外,很重要的是,Verlinde图像无法用到热力学上,对于一个气体,很难获得可以接受的熵公式。
我建议大家读我们的文章。
当然,不用说,还有很多要做的研究。
Temperature is defined as the conjugate variable to energy
The force is entirely a consequence of the amount of configuration space and not mediated by anything. There is no space yet.
Erik Verlinde: comments about the entropic force of gravity
Written by Dr Erik Verlinde (see Twitter)
 Logic of the paper
Logic of the paper
The paper (abs, PDF) is not technical, but some background is needed, more than just being able to read the text and the equations. The text explains the logic, but apparently some important points are misunderstood. Clearly, I should do a better job in making them more clear. But it is my impression that the misunderstanding is partly due to a lack of background or a difference in reference frame. Because the logic of the paper is being misrepresented in some reports, I add here some clarifications.
So here is an attempt to address some of the points that I think are not appreciated or generally understood.
Temperature is defined as the conjugate variable to energy. Geometrically it can be identified with the periodicity of euclidean time that is obtained after analytic continuation. Again there is nothing needed about space. Temperature exists if there is only time.
It is possible to introduce other macroscopic variables that are associated with a finite but still large subset of the microstates. Let us denote such a variable by x, at this point this is just some arbitrary choice. It can be any macroscopic variable that singles out a collection of the microscopic states. So specifying x in addition the to energy gives more detailed description of the microscopic states, but nothing more. So it is not even necessary to think about x as a space coordinate. Nevertheless one can define a number of microstates denoted by Omega(E,x) for given energy E and for a given value x for this macroscopic variable x.

Next one can introduce a formal variable called F and introduce in the partition function as the thermodynamical dual to x. Following just standard statistical physics (I avoid the word mechanics, since Newton's law is not necessary) one can obtain the 1st law of thermodynamics.
The meaning of the statement that space is emergent is that the space coordinates x can be viewed as examples of such macroscopic variables. They are not microscopically defined, but just introduced as a way of singling out part of the available micro states. It is my impression that not all readers have understood or appreciated this essential point. Hence, if the number of states depend on x there can be an entropic force, when there is a finite temperature. This is all, nothing more. Again, for this point I don't need to assume Newtonian mechanics. It does not exist yet in this framework.
The other central point paper is that if one chooses a macroscopic coordinate x that corresponds to a fixed position in a non-inertial frame, that Newton's law of inertia
The other formulas presented in the paper are just there to illustrate that indeed it is possible to get gravity from this kind of reasoning, and that it is consistent with the ideas of holography. But the main point concerns the law of inertia. The derivation of the Einstein equations (and of Newton's law in the earlier sections) follows very similar reasonings that exist in the literature, in particular Jacobson's. The connection with entropy and thermodynamics is made also there. But in those previous works it is not clear WHY gravity has anything to do with entropy. No explanation for this apparent connection between gravity and entropy has been given anywhere in the literature. I mean not the precise details, even the reason why there should be such a connection in the first place was not understood.
My paper is the first that gives a reason why. Inertia, and hence motion, is due to an entropic force when space is emergent. This is new, and the essential point. This means one HAS TO keep track of the amount of information. Differences in this amount of information is precisely what makes one frame an inertial frame, and another a non-inertial frame. Information causes motion.
This can be derived without assuming Newtonian mechanics.
So the logic of the part of the paper dealing with inertia is:
This way of turning the logic of an existing argument around is done more often in physics, and it is known to lead to much more clear formulations of a theory. The example that comes to mind is the way that Dirac used the result of Heisenberg that p and q do not commute, which was obtained in some roundabout way, and made it in to the starting point for quantum mechanics. This is how it is being taught today.
Anyhow, I hope this clarifies some points, and removes some of the misunderstandings.
The essential new points of the paper
I have noticed another point of the paper that is not appreciated in blog discussions. For many years, there have been previous works in the literature that discuss the similarity between gravity and thermodynamics. In particular in Jacobson's work there is a clear statement that if one assumes the first law of thermodynamics, the holographic principle, and identifies the temperature with the Unruh temperature, that one can derive the Einstein equations. This is a remarkable result. Yet it is already 12 years old, and still up to this day, gravity is seen as a fundamental force. Clearly, we have to take these analogies seriously, but somehow no one does.
I studied the previous papers very well, and know about them for years. Many people have. We have seen a recent increase in papers following Jacobson, and extending his work to higher derivative gravity, and so. But from all of these papers, I did not pick up the insights I presented in this paper. What was missing from those papers is the answer to questions like: why does gravity have anything to do with entropy? Why do particles follow geodesics? What has entropy to do with geometry?
The derivation of Jacobson does not take in to account the fact that the mass of an object and therefore its energy can change due to the displacement of matter far away from it. There is action at a distance hidden in gravity, even relativistically. The ADM and Komar definitions of mass make this non-local aspect of gravity very clear. This non-local aspect of gravity is precisely what the holographic principle is about.
Jacobson's argument is ultra local, and assumes the presence of stress energy crossing the horizon. But there is no statement about an entropic force that is influencing particles far away from the horizon. My point of view is an attempt to take a much more global view, and map out the information over a bigger part of space, even though initially I can only do that for static space times.
The statement that gravity is an entropic force is more then just saying that "it has something to do with thermodynamics". It says that motion and forces are the consequence of entropy differences. My idea is that in a theory in which space is emergent forces are based on differences in the information content, and that very general random microscopic processes cause inertia and motion. The starting point from which this all can be derived can be very, very general. In fact we don't need to know what the microscopic degrees of freedom really are. We only need a few basic properties.
For me this was an "eye opener", it made it from obscure to obvious. It is clear to me know that it has to be this way. There is no way to avoid it: if one does not keep track of the amount of information, one ignores the origin of motion and forces. It clarifies why gravity has something to do with entropy. It has to, it can not do otherwise.
When I got the idea that gravity and inertia emerge in this way, which is close to half a year ago, I was really excited. I felt I had an insight that makes clear what gravity is. But I decided not to publish too quickly, also to allow time to make it more precise. But also to see if the idea that gravity is entropic would still appear to me as new as exciting as my first feeling about it. And it does. Now, almost half a year later, I still feel that way.
For instance, the similarity between the entropic force for a polymer and gravity is a real clue to something important. The fact that it fits in well with an adapted version of the work of Jacobson gives additional support. The derivation of the Einstein equations is not really new, in my mind, since it technically is very similar to the previous works. And I agree that the other line of the paper that discusses inertia is heuristic, and leaves some important gaps. But nevertheless I decided to publish it anyway, because I think this approach to gravity is the right one, it is different, very different from everything that is done today.
Everyone who does not appreciate that this view is different from previous papers are missing an essential point. If space is emergent, a lot more has to be explained than just the Einstein equations. Geodesic motion, or if you wish, the laws of Newton have to be re-derived. They are not fundamental. This has not been discussed anywhere, not even noted that it is the case.
If the previous papers had made the emergence of gravity so clear, why are people still regarding string theory as the final theory of quantum gravity? Somehow, not everyone was convinced that these similarities mean something, or at least, people had no clear idea of what they mean.
Some people may think that when we develop string theory further that eventually we will learn about this. I am not sure that string theory is the way to go. In any case, not if we keep regarding the definition in terms of closed strings as being microscopically defined, may be equivalent to some other formulation. And not if we keep our eyes closed for emergent phenomena. Graviton's can not be fundamental particles in a theory of emergent space time and gravity.
So what is the role of string theory, if gravity is emergent? I discussed this at some level in the paper. It should also be emergent, and it is nothing but a framework like quantum field theory.
In fact, I think of string theory as the way to make QFT in to a UV complete but still effective framework. It is based on universality. Many microscopic systems can lead to the same string theory. The string theory landscape is just the space of all universality classes of this framework. I have more to say about it, but will keep that for a publication, or I will post that some other time.
Of course, I would have liked to make things even more clear or convincing. In this paper, I use heuristic and you might say handwaving arguments. The issue of motion: why is the acceleration a that I introduced equal to the second time derivative of the position? If one assumes the equivalence principle, it is clear. Also coordinate invariance would be enough. But I do not have a very precise way of seeing how that emerges. How to go from just information to a Lorentzian geometry in which general coordinate invariance is manifest. Some assumptions have to be made.
But again, this are questions that others have not been even started to think about. These are questions that have not been even addressed by previous works. But they are essential. When one really understands this well, there should be no doubt that gravity is emergent and forces are driven by entropy.
This is the essential idea, which is really new and important, and which in my view justifies this level of reasoning, certainly in a first paper. It is clear that this is not the final paper on this subject. This is also my own view. I clearly did not answer all of the questions. In fact, my approach probably raises more questions than it answers. But it should be obvious that these questions are important, very fundamental and their answers should lead us in a completely new direction. Our theories will have to based on new paradigms.
I find all this still very exciting and will continue to work in this direction.
And remember, quantum mechanics was also not developed in one paper. Do you think de Broglie knew exactly what he was talking about? Leaps based in intuition are sometimes necessary. They are an important part of progress in science, even if they do not immediately give complete finished theories of Nature.
Comments about irreversibility
Entropic forces and the 2nd law of thermodynamics
15/01/10 02:21
Let me address some other confusions in the blog discussion. The fact that a force is entropic does not mean it should lead to irreversible processes. This is a complete misunderstanding of what it means to have an entropic force. This is why I added section 2 on the entropic force. For a polymer the force obeys Hooke's law, which is perfectly conservative. No doubt about that.
Just last week we had a seminar in Amsterdam on DNA. Precisely the situation described in section two was performed in lab experiments, using optical tweezers. The speaker, Gijs Wuite from the Free University in Amsterdam, showed movies of DNA being stretched and again released. These biophysicists know very well that these forces are purely entropic, and conservative. The processes that involve these forces are for all practical purposes reversible. Indeed, the movies that were shown clearly exhibited this reversibility, to a very high degree. In fact, I asked the speaker specifically about this, and he confirmed it. They test this in the lab, so it is an experimental fact that entropic forces can be conservative.
I explained this in section 2. So please read it again, study it and think about it for a little longer. When the heat bath is infinite, the force is perfectly conservative. For the case of gravity the speed of light determines the size of the heat bath, since its energy content is given by E=Mc^2. So in the non relativistic limit the heat bath is infinite. Indeed, Newton's laws are perfectly conservative. When one includes relativistic effects, the heat bath is no longer infinite. Here one could expect some irreversibility. In fact, I suspect that the production of gravity waves is causing this. Indeed, a binary system will eventually coalesce. This is irreversible, indeed. This all fits very well, extremely well, actually with the fact that gravity is an entropic force. Of course, when I first got these ideas, I worried also about irreversiblity. I knew about the polymer example, but had to study it again to convince myself that entropic forces can indeed be conservative. But it is a well known fact for biophysicists.
Another useful point to know is that when a system is slightly out of equilibrium, it will indeed generate some entropy. But a theorem by Prigogine states that the dynamics of the system will adapt itself so that entropy production is minimized. Yes, really minimized. This may appear counterintuitive, but I like to look at it as that it seeks the path of least resistance. So this means that there ill in general not be a lot of entropy generated. At least, the system will do whatever it can to minimize it.
By the way, it is true that the total energy of a system of two masses m_1 and m_2 is given by the total mass M=m_1+m_2. But the natural expression for the entropy gradient due to change in relative position is that instead of being proportional to the smalles mass, that it is proportional to the reduced mass m_1m_2/(m_1+m_2). This is the only natural expression that is symmetric in m_1 and m_2. And indeed, by the same argument as in the paper one recovers the right force. I thought of putting that in the paper, but I thought it was kind of trivial. This point of confusion is not difficult to solve, it seems to me.
Another point that may not be appreciated is that the system is actually taken out of equilibrium. If everything would be in equilibrium, the universe would be a big black hole, or be described by pure de Sitter space. Only horizons, no visible matter. If a system is out of equilibrium, there is not a very precise definition of temperature. In fact, different parts of the system may have different temperatures. This means that there is no problem also with neutron stars. In fact, I got these ideas precisely by thinking about what causes neutron stars to collapse if one considers them from a holographic perspective. I concluded that the cause was purely entropic. By the way, physical neutron stars do not have exact zero temperature. But the temperature I use in the paper is one that is associated with the microscopic degrees of freedom, which because there is no equilibrium, is not necessarily equal to the macroscopic temperature.
The microscopic degrees of freedom on the holographic screens should not be seen as being associated with local degrees of freedom in actual space. They are very non local states. This is what holography tells us. In fact, they can also not be only related to the part of space contained in the screen, because this would mean we can count micro states independently for every part of space, and in this way we would violate the holographic principle. There is non locality in the microstates.
Another point: gravitons do not exist when gravity is emergent. Gravitons are like phonons. In fact, to make that analogy clear consider two pistons that close of a gas container at opposite ends. Not that the force on the pistons due to the pressure is also an example of an entropic force. We keep the pistons in place by an external force. When we gradually move one of the pistons inwards by increasing the force, the pressure will become larger. Therefore the other piston will also experience a larger force. We can also do this in an abrupt way. We then cause a sound wave to go from one piston to the other. The quantization of this sound wave leads to phonons. We know that phonons are quite useful concepts, which even themselves are often used to understand other emergent phenomena.
Similarly, gravitons can be useful, and in that sense exist as effective "quasi" particles. But they do not exist as fundamental particles.
Table of contents:
► Logic of the paper (right below)
► The essential new points of the paper (click)
► Comments about irreversibility (click)
 Logic of the paper
Logic of the paperThe paper (abs, PDF) is not technical, but some background is needed, more than just being able to read the text and the equations. The text explains the logic, but apparently some important points are misunderstood. Clearly, I should do a better job in making them more clear. But it is my impression that the misunderstanding is partly due to a lack of background or a difference in reference frame. Because the logic of the paper is being misrepresented in some reports, I add here some clarifications.
So here is an attempt to address some of the points that I think are not appreciated or generally understood.
Previous article on the same topic: Gravity as a holographic entropic force and Why gravity can't be an entropic forceThe starting point is a microscopic theory that knows about time, energy and number of states. That is all, nothing more. This is sufficient to introduce thermodynamics. From the number of states one can construct a canonical partition function, and the 1st law of thermodynamics can be derived. No other input is needed, certainly not Newtonian mechanics. Time translation symmetry gives by Noether's theorem a conserved quantity. This defines energy. Hence, the notion of energy is already there when there is just time, no space is needed.
Temperature is defined as the conjugate variable to energy. Geometrically it can be identified with the periodicity of euclidean time that is obtained after analytic continuation. Again there is nothing needed about space. Temperature exists if there is only time.
It is possible to introduce other macroscopic variables that are associated with a finite but still large subset of the microstates. Let us denote such a variable by x, at this point this is just some arbitrary choice. It can be any macroscopic variable that singles out a collection of the microscopic states. So specifying x in addition the to energy gives more detailed description of the microscopic states, but nothing more. So it is not even necessary to think about x as a space coordinate. Nevertheless one can define a number of microstates denoted by Omega(E,x) for given energy E and for a given value x for this macroscopic variable x.

Next one can introduce a formal variable called F and introduce in the partition function as the thermodynamical dual to x. Following just standard statistical physics (I avoid the word mechanics, since Newton's law is not necessary) one can obtain the 1st law of thermodynamics.
dE = T dS - F dx.This makes clear that F is a generalized "force", but it has nothing to do with Newton's law yet. It is defined in terms of entropy differences. The macroscopic force that is obtained in this way has no microscopic origin in terms of microscopic field. The force is entirely a consequence of the amount of configuration space and not mediated by anything. There is no space yet.
The meaning of the statement that space is emergent is that the space coordinates x can be viewed as examples of such macroscopic variables. They are not microscopically defined, but just introduced as a way of singling out part of the available micro states. It is my impression that not all readers have understood or appreciated this essential point. Hence, if the number of states depend on x there can be an entropic force, when there is a finite temperature. This is all, nothing more. Again, for this point I don't need to assume Newtonian mechanics. It does not exist yet in this framework.
The other central point paper is that if one chooses a macroscopic coordinate x that corresponds to a fixed position in a non-inertial frame, that Newton's law of inertia
F = mawill be the consequence of such an entropic force. This has to be. There is no other way it can arise, simply because x is not a microscopic variable. It is obvious. Nevertheless, it is a fundamental new insight that has not been noted before. This is not an empty or circular statement. It says something about the way that the function Omega(E,x) should behave as a function of x. All this can be derived and defined without the input of Newtonian mechanics.
The other formulas presented in the paper are just there to illustrate that indeed it is possible to get gravity from this kind of reasoning, and that it is consistent with the ideas of holography. But the main point concerns the law of inertia. The derivation of the Einstein equations (and of Newton's law in the earlier sections) follows very similar reasonings that exist in the literature, in particular Jacobson's. The connection with entropy and thermodynamics is made also there. But in those previous works it is not clear WHY gravity has anything to do with entropy. No explanation for this apparent connection between gravity and entropy has been given anywhere in the literature. I mean not the precise details, even the reason why there should be such a connection in the first place was not understood.
My paper is the first that gives a reason why. Inertia, and hence motion, is due to an entropic force when space is emergent. This is new, and the essential point. This means one HAS TO keep track of the amount of information. Differences in this amount of information is precisely what makes one frame an inertial frame, and another a non-inertial frame. Information causes motion.
This can be derived without assuming Newtonian mechanics.
So the logic of the part of the paper dealing with inertia is:
microscopic theory without space or laws of Newton → thermodynamics → entropic force → inertia.The part that deals with gravity assumes holography as additional input. But this is just like what has been done before. It is also not the main point of the paper. Gravity in a way does not exist in Einstein's theory either. But one would like to recover the gravity equations. The logic here is
thermodynamics + holographic principle → gravity.The obvious question is of course, where does the holographic principle come from? Of course, it was extracted from the physics of black holes. But the holographic principle can be formulated without reference to black holes or gravity. Hence, it can be taken as a starting point, from which one then subsequently derive gravity. Again, this part is in essence not new. Jacobson followed exactly the same logic.
This way of turning the logic of an existing argument around is done more often in physics, and it is known to lead to much more clear formulations of a theory. The example that comes to mind is the way that Dirac used the result of Heisenberg that p and q do not commute, which was obtained in some roundabout way, and made it in to the starting point for quantum mechanics. This is how it is being taught today.
Anyhow, I hope this clarifies some points, and removes some of the misunderstandings.
The essential new points of the paper
I have noticed another point of the paper that is not appreciated in blog discussions. For many years, there have been previous works in the literature that discuss the similarity between gravity and thermodynamics. In particular in Jacobson's work there is a clear statement that if one assumes the first law of thermodynamics, the holographic principle, and identifies the temperature with the Unruh temperature, that one can derive the Einstein equations. This is a remarkable result. Yet it is already 12 years old, and still up to this day, gravity is seen as a fundamental force. Clearly, we have to take these analogies seriously, but somehow no one does.
I studied the previous papers very well, and know about them for years. Many people have. We have seen a recent increase in papers following Jacobson, and extending his work to higher derivative gravity, and so. But from all of these papers, I did not pick up the insights I presented in this paper. What was missing from those papers is the answer to questions like: why does gravity have anything to do with entropy? Why do particles follow geodesics? What has entropy to do with geometry?
The derivation of Jacobson does not take in to account the fact that the mass of an object and therefore its energy can change due to the displacement of matter far away from it. There is action at a distance hidden in gravity, even relativistically. The ADM and Komar definitions of mass make this non-local aspect of gravity very clear. This non-local aspect of gravity is precisely what the holographic principle is about.
Jacobson's argument is ultra local, and assumes the presence of stress energy crossing the horizon. But there is no statement about an entropic force that is influencing particles far away from the horizon. My point of view is an attempt to take a much more global view, and map out the information over a bigger part of space, even though initially I can only do that for static space times.
The statement that gravity is an entropic force is more then just saying that "it has something to do with thermodynamics". It says that motion and forces are the consequence of entropy differences. My idea is that in a theory in which space is emergent forces are based on differences in the information content, and that very general random microscopic processes cause inertia and motion. The starting point from which this all can be derived can be very, very general. In fact we don't need to know what the microscopic degrees of freedom really are. We only need a few basic properties.
For me this was an "eye opener", it made it from obscure to obvious. It is clear to me know that it has to be this way. There is no way to avoid it: if one does not keep track of the amount of information, one ignores the origin of motion and forces. It clarifies why gravity has something to do with entropy. It has to, it can not do otherwise.
When I got the idea that gravity and inertia emerge in this way, which is close to half a year ago, I was really excited. I felt I had an insight that makes clear what gravity is. But I decided not to publish too quickly, also to allow time to make it more precise. But also to see if the idea that gravity is entropic would still appear to me as new as exciting as my first feeling about it. And it does. Now, almost half a year later, I still feel that way.
For instance, the similarity between the entropic force for a polymer and gravity is a real clue to something important. The fact that it fits in well with an adapted version of the work of Jacobson gives additional support. The derivation of the Einstein equations is not really new, in my mind, since it technically is very similar to the previous works. And I agree that the other line of the paper that discusses inertia is heuristic, and leaves some important gaps. But nevertheless I decided to publish it anyway, because I think this approach to gravity is the right one, it is different, very different from everything that is done today.
Everyone who does not appreciate that this view is different from previous papers are missing an essential point. If space is emergent, a lot more has to be explained than just the Einstein equations. Geodesic motion, or if you wish, the laws of Newton have to be re-derived. They are not fundamental. This has not been discussed anywhere, not even noted that it is the case.
If the previous papers had made the emergence of gravity so clear, why are people still regarding string theory as the final theory of quantum gravity? Somehow, not everyone was convinced that these similarities mean something, or at least, people had no clear idea of what they mean.
Some people may think that when we develop string theory further that eventually we will learn about this. I am not sure that string theory is the way to go. In any case, not if we keep regarding the definition in terms of closed strings as being microscopically defined, may be equivalent to some other formulation. And not if we keep our eyes closed for emergent phenomena. Graviton's can not be fundamental particles in a theory of emergent space time and gravity.
So what is the role of string theory, if gravity is emergent? I discussed this at some level in the paper. It should also be emergent, and it is nothing but a framework like quantum field theory.
In fact, I think of string theory as the way to make QFT in to a UV complete but still effective framework. It is based on universality. Many microscopic systems can lead to the same string theory. The string theory landscape is just the space of all universality classes of this framework. I have more to say about it, but will keep that for a publication, or I will post that some other time.
Of course, I would have liked to make things even more clear or convincing. In this paper, I use heuristic and you might say handwaving arguments. The issue of motion: why is the acceleration a that I introduced equal to the second time derivative of the position? If one assumes the equivalence principle, it is clear. Also coordinate invariance would be enough. But I do not have a very precise way of seeing how that emerges. How to go from just information to a Lorentzian geometry in which general coordinate invariance is manifest. Some assumptions have to be made.
But again, this are questions that others have not been even started to think about. These are questions that have not been even addressed by previous works. But they are essential. When one really understands this well, there should be no doubt that gravity is emergent and forces are driven by entropy.
This is the essential idea, which is really new and important, and which in my view justifies this level of reasoning, certainly in a first paper. It is clear that this is not the final paper on this subject. This is also my own view. I clearly did not answer all of the questions. In fact, my approach probably raises more questions than it answers. But it should be obvious that these questions are important, very fundamental and their answers should lead us in a completely new direction. Our theories will have to based on new paradigms.
I find all this still very exciting and will continue to work in this direction.
And remember, quantum mechanics was also not developed in one paper. Do you think de Broglie knew exactly what he was talking about? Leaps based in intuition are sometimes necessary. They are an important part of progress in science, even if they do not immediately give complete finished theories of Nature.
Comments about irreversibility
Entropic forces and the 2nd law of thermodynamics
15/01/10 02:21
Let me address some other confusions in the blog discussion. The fact that a force is entropic does not mean it should lead to irreversible processes. This is a complete misunderstanding of what it means to have an entropic force. This is why I added section 2 on the entropic force. For a polymer the force obeys Hooke's law, which is perfectly conservative. No doubt about that.
Just last week we had a seminar in Amsterdam on DNA. Precisely the situation described in section two was performed in lab experiments, using optical tweezers. The speaker, Gijs Wuite from the Free University in Amsterdam, showed movies of DNA being stretched and again released. These biophysicists know very well that these forces are purely entropic, and conservative. The processes that involve these forces are for all practical purposes reversible. Indeed, the movies that were shown clearly exhibited this reversibility, to a very high degree. In fact, I asked the speaker specifically about this, and he confirmed it. They test this in the lab, so it is an experimental fact that entropic forces can be conservative.
I explained this in section 2. So please read it again, study it and think about it for a little longer. When the heat bath is infinite, the force is perfectly conservative. For the case of gravity the speed of light determines the size of the heat bath, since its energy content is given by E=Mc^2. So in the non relativistic limit the heat bath is infinite. Indeed, Newton's laws are perfectly conservative. When one includes relativistic effects, the heat bath is no longer infinite. Here one could expect some irreversibility. In fact, I suspect that the production of gravity waves is causing this. Indeed, a binary system will eventually coalesce. This is irreversible, indeed. This all fits very well, extremely well, actually with the fact that gravity is an entropic force. Of course, when I first got these ideas, I worried also about irreversiblity. I knew about the polymer example, but had to study it again to convince myself that entropic forces can indeed be conservative. But it is a well known fact for biophysicists.
Another useful point to know is that when a system is slightly out of equilibrium, it will indeed generate some entropy. But a theorem by Prigogine states that the dynamics of the system will adapt itself so that entropy production is minimized. Yes, really minimized. This may appear counterintuitive, but I like to look at it as that it seeks the path of least resistance. So this means that there ill in general not be a lot of entropy generated. At least, the system will do whatever it can to minimize it.
By the way, it is true that the total energy of a system of two masses m_1 and m_2 is given by the total mass M=m_1+m_2. But the natural expression for the entropy gradient due to change in relative position is that instead of being proportional to the smalles mass, that it is proportional to the reduced mass m_1m_2/(m_1+m_2). This is the only natural expression that is symmetric in m_1 and m_2. And indeed, by the same argument as in the paper one recovers the right force. I thought of putting that in the paper, but I thought it was kind of trivial. This point of confusion is not difficult to solve, it seems to me.
Another point that may not be appreciated is that the system is actually taken out of equilibrium. If everything would be in equilibrium, the universe would be a big black hole, or be described by pure de Sitter space. Only horizons, no visible matter. If a system is out of equilibrium, there is not a very precise definition of temperature. In fact, different parts of the system may have different temperatures. This means that there is no problem also with neutron stars. In fact, I got these ideas precisely by thinking about what causes neutron stars to collapse if one considers them from a holographic perspective. I concluded that the cause was purely entropic. By the way, physical neutron stars do not have exact zero temperature. But the temperature I use in the paper is one that is associated with the microscopic degrees of freedom, which because there is no equilibrium, is not necessarily equal to the macroscopic temperature.
The microscopic degrees of freedom on the holographic screens should not be seen as being associated with local degrees of freedom in actual space. They are very non local states. This is what holography tells us. In fact, they can also not be only related to the part of space contained in the screen, because this would mean we can count micro states independently for every part of space, and in this way we would violate the holographic principle. There is non locality in the microstates.
Another point: gravitons do not exist when gravity is emergent. Gravitons are like phonons. In fact, to make that analogy clear consider two pistons that close of a gas container at opposite ends. Not that the force on the pistons due to the pressure is also an example of an entropic force. We keep the pistons in place by an external force. When we gradually move one of the pistons inwards by increasing the force, the pressure will become larger. Therefore the other piston will also experience a larger force. We can also do this in an abrupt way. We then cause a sound wave to go from one piston to the other. The quantization of this sound wave leads to phonons. We know that phonons are quite useful concepts, which even themselves are often used to understand other emergent phenomena.
Similarly, gravitons can be useful, and in that sense exist as effective "quasi" particles. But they do not exist as fundamental particles.
No comments:
Post a Comment