人脑之谜
苏珊·格林菲尔德/著 杨雄里等/译| 序言 | |||||
| 第01章 | 脑中之脑 | 第02章 | 脑的活动 | 第03章 | 神经冲动 |
| 第04章 | 脑的发育 | 第05章 | 记忆之谜 | ||
| 结论和前瞻 | |||||
| 译者后记 | |||||
最后那个电子入住的房间的高度（能量）的数值，便是费米能级。
金属的费米面是零度时电子真正占据的最高能级，不像半导体，费米能级在能隙中，并不是真正存在的能级。
《硅火燎原》-10-费米能级
精选
|||
10.费米能级
费米能级（Fermi Level）是半导体物理中的重要概念，不可不知。
前面几节中介绍的能带图，描述了晶体中的电子所可能具有的能量值。打个不十分恰当的比喻，能带图就好比是在一个蜿蜒连绵的山区中，沿着高高低低、层层重叠的山坡谷底，建造了许许多多的房子。每种晶体有各自独特的建房方案。所有这些房子都是单间房，因为电子绝不与别人同居。每间房子，电子可能住进去了，也可能还没住。电子到底住没住？住进某个房间的几率是多少？一定的条件下，电子是如何分布在这些房间中的？很遗憾，这些从能带图上看不出来。那么，哪一个参数才会告诉我们这些信息呢？这个参数就是费米能级。
所以，费米能级并不高深神秘，只是具有能量量纲的某个数值而已。不过，一个参数就能供给我们这么多的信息，这个数值也还是挺神的。
费米能级可以告诉我们电子的分布情况，所以应该和统计现象有关。
物理学中有3种不同的统计规律：波尔兹曼统计、波色爱因斯坦统计、和费米狄拉克统计。它们分别适用于三种不同性质的微观粒子：经典粒子、玻色子、和费米子。相对于经典粒子而言，玻色子和费米子服从量子力学的规律。从统计观点来看，它们和经典粒子的不同之处是在于它们的不可区分性，或者说，玻色子和费米子是全同粒子。
什么是全同粒子呢？所谓全同粒子就是质量、电荷、自旋等内在性质完全相同的粒子。以经典力学的观点，即使两个粒子的上述性质全同，它们也仍然可以从运动的不同轨道而被区分。但在量子力学中，由于测不准原理，粒子没有确定的轨道，因而当两个粒子间距大大小于它们的德布罗意波长时，就无法区分了。至于费米子和玻色子的不同秉性，我们曾经描述过一点点儿：费米子是独行侠，就像电子那样，必须每人单独住一间房，而玻色子呢，则可以群居。
这3种粒子本性的不同，又如何影响它们的统计分配规律呢？让我们从一个简单的例子：两个粒子（A、B）分住三间房子（F1、F2、F3）的情况，来体会这点。
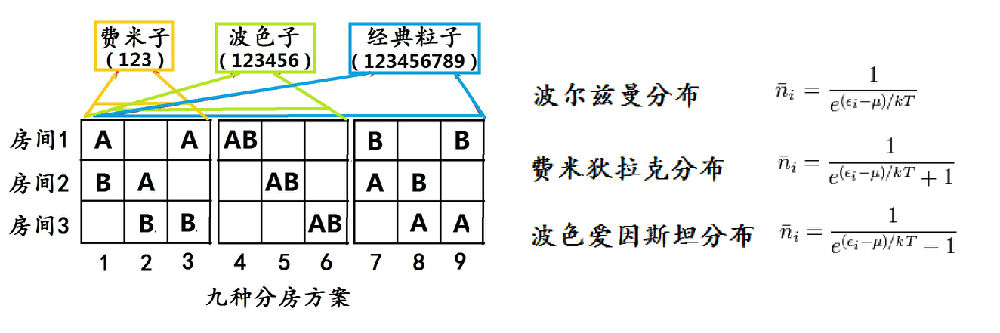
图10.1
我们最熟悉的是经典粒子，就是等同于两个‘人’住3间房子的情况，可能的方案有图10中所示的9种。因此，两个经典粒子入住的方法共有9种。如果这两个粒子是费米子，则入住的方式只有1、2、3这三种。这是因为费米子遵循泡利不相容原理而排除了方案4、5、6；又因为它们无法被区分而使得7、8、9完全等同于1、2、3。对两个玻色子来说，它们也不能被区分，但可以同住一间，所以便有1到6六种分配方法。
有的读者可能会问：“一间房是什么意思呢？是不是一个能级呢？”其实不是这样，这也是从能带图上看不出来的。更确切地说，一间房是指一个量子态。不同的量子态由不同的量子数来决定。同样的能量数值，还可以有多个量子态，因为还可以有诸如角动量、自旋等等的不同。
另外，这三种粒子，还有一个共同具有的有趣性质：大家都喜欢住在低处，即能量更小的地方。特别是在温度接近绝对零度左右时，这些小粒子们的运动几乎停止了，一个个疲惫不堪，苟延残喘，只要有可能，便都拼命想往低处靠，好像越低越保险似的。所以，经典粒子和玻色子在接近00T时，全部都挤在那个最底层的大房子里，就像无家可归者挤在难民营里一样，反正又没有什么‘泡利不相容原理’来限制它们。
这时，费米子倒显出一点骨气，它们仍然坚持自己要独居的风格，井井有条地一个一个排队入住到给它们打造的‘单间’量子态中。由于它们要遵循泡利不相容原理，所以就不可能所有的电子都住在底层，底层住满后便第1、2、……地排上去。粗略地说，最后那个电子入住的房间的高度（能量）的数值，便是费米能级。为什么这儿加上个‘粗略地说’呢，这是因为要精确地定义费米能级，是需要用点不怎么讨人喜欢的公式的。
总之，大家现在明白了，费米能级的概念的确很简单，不就是一个能量数值的标准吗。从刚才所说的意思，假设任何高度都连续地建有房间的话，那么，在这个标准之下，房间全被住满了；而在这个标准之上的房间则全部空着。
以上的理解完全正确。不过，刚才所说的是接近绝对零度时的情况。如果温度升高一些，情况则略有不同。温度升高了，电子的动能增加了，它们不像原来那么老实了，而是在房间里跳来跳去，也不太屑于那种要‘住得低一些’的老观念，而是四处窥探有无可乘之机！住在比较下面的电子伸头一看，周围房间上上下下全都住满了，太高的地方又跳不上去，所以，只好仍然规规矩矩地在原处待着，集聚更多的内力，等待温度再升高。而那些靠近费米能级、原来就住得比较高的电子就有所希望啦。它们有的已经蹦到比费米能级还高的地方去了。温度越高，电子上蹦成功的可能性就越大。
所以，当绝对温度T不为0的时候，费米能级并不是‘住了电子’，还是‘没住电子’的分界线。但是，对这种情况，物理学家费米和狄拉克，各自独立地导出了一个同样的公式。看，公式终于出现了，这就是我们现在称之为费米狄拉克统计分布的公式：
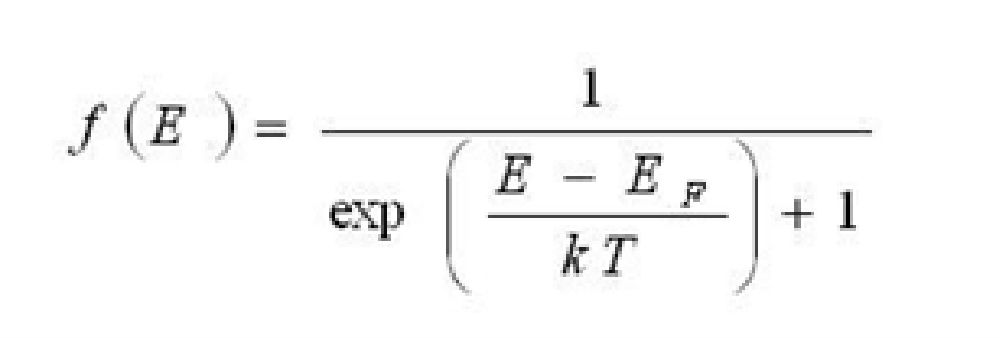(10.1)
公式（10.1）中的EF就是费米能级，f（E）是占据能量为E量子态的电子数目。所以说，费米能级虽然只是一个数，但是，知道了这个数，就知道了在某一个温度下，电子入住各个房间的分配情况。这些房间的高度（E）可以低于费米能级，也可以高于费米能级，只是电子住或不住的几率有所不同而已。这儿的‘几率’便与表达式（10.1）有关。
综上所述，温度升高时，只有费米能级附近的电子才容易跳来蹦去，参与热跃迁，或产生电荷的输运过程。而这也正是固体表现导电或不导电，决定各种物理性质的机制所在。所以，在能带图中，我们感兴趣的也只是费米能级附近的能带结构，因为它们决定了电子（或空穴）的输运性质。
图10.2：费米能级在不同材料能带图中的位置
在上一节中我们描述了第一布里渊区，它是波矢空间中的一块区域。在波矢空间中还定义了另一个与费米能级有关的区域，叫做费米面。
又有点迷惑吧？费米能级不是一个数吗，怎么又变成一个面了呢？一个数变成一个面其实不难，比如说，给你一个数作为半径，你立刻可以在三维空间中画出一个球面来。费米面也是用这样类似方法画出来的，只不过不是在真实的三维坐标空间中画，而是在三维的波矢空间（k空间）里画的。换句话说，费米面是在k空间中的一个等能量面，这个面上的点的k值（kx,ky,kz）不同，但对应的能量数值却是相同的，等于费米能级与最低能量态的差别，或称‘费米能’。
这里需要提醒读者注意：我们从费米狄拉克统计规律（10.1），定义了‘费米能级（FermiLevel）’，刚才又提到‘费米能（Fermi Energy）’。这在某些场合，比如处理费米气体的情况，是相关但不完全相同的两个概念。不过在半导体文献中却经常被混淆地用作同义词。因此，我们也不严格区分它们，只不过一般只说‘费米能级’。
现在，考察一下第7节中讨论过的自由电子，也就是忽略晶格离子作用时，能带为抛物线的那种情况。这时，能量正比于k矢量绝对值的平方，因此，等能量面都是球面，自由电子的费米面没有例外，当然也是球面。既然自由电子的费米面是球面，也就有了费米球、费米海、费米半径之类的相应定义。
http://blog.sciencenet.cn/blog-677221-704478.html 转载请注明来自科学网博客，并请注明作者姓名。
上一篇：《硅火燎原》-9-布洛赫波和布里渊区
下一篇：《硅火燎原》-11-半导体的能带
15 罗德海 李铭 卢翔孟 梁先庭 张启峰 吴吉良 王国强 姚向峰 林涛 王涛 石磊 王伟 lengyonggang nnxxsh vivikzw
该博文允许注册用户评论 请点击登录 评论 (11 个评论)
- [11]张阳东
- 哈哈，一楼刚好提了我想问的，当T趋于0时的化学势等于费米能吧。
- 博主回复(2015-1-15 20:31)：费米能是T=0时基态的化学势
- [10]mirrorliwei
- 这段的处理也不是很好。与前边的篇章的有机链接还嫌不够。布局和结构，需要摊在大纸上去画出关联后在重构一下与此相关的个篇。
- [9]朱寅
- 张老师
非常感谢你的系列科普。这对我这样的非常物理学专业而喜爱物理学的人来说是个很大的帮助。
我现在正在读两篇文献：
[1] Alberto Peruzzo, et al, A Quantum Delayed-Choice Experiment，Science 338, 634 (2012)
[2] D. Salart, et al, Testing spooky action at a distance, Nature 454, 861-864 (2008)
对这个表述：Hence, both aspects, particle and wave, which appear to be incompatible, are never observed simultaneously.[1] 好象没有看到过，不知道怎样理解。
我以前读过：
[3] L. J. Wang, et al, Gain-assisted superluminal light propagation, Nature 406, 277-279 (2000)
我一直没有搞懂：“还没有出发就已经到达”是一种什么情况。
这三篇论文都与惠勒有关，同时，也都有（或主要是）关于Nonlocal的问题。如果你能就这一问题写一个科普，可能对很多人（首先是对我）都有帮助。
同时，我觉得文献[1]与
[4]S. Deleglise, I. Dotsenko, C. Sayrin, J. Bernu, M. Brune,J. M. Raimond, S. Haroche，Reconstruction of non-classicalcavity field states with snapshots of their decoherence. Nature, 2008. 455:510
有某种关系。但我还说不好这是什么关系。
----------------------------------------------------------------------------------
这是一个不期之请。如果你没有时间或其他原因，完全可以不予理会。 - 博主回复(2013-7-8 08:29)：谢谢你提供的文献，有时间时我会去看看。
- [8]nnxxsh
- 8、9、10写得真好，又看了两遍，急切地等待下文
- 博主回复(2013-7-3 19:29)：谢谢关注。
- [7]欧阳峰
- 把这个概念写得那么易懂又准确真不容易，赞一个！
公式１０.１的解释是“电子数”，书上是这么说的。但我觉得对外行者不容易懂，因为这个数总是小于一的。我不知道为什么人们不说“电子占据的几率”？还是其中涉及的进出平衡的归一化问题？
另外，最后讲到波矢空间是似乎没有给出定义，也许在以前章节中介绍过了吧。但把波矢空间与前面说的“小房子”联系起来也许是个好主意。 - 博主回复(2013-7-3 19:32)：谢谢来访。同意你的意见，应该说：电子占据的几率。
- [6]nnxxsh
- 写得好精彩，一口气看完，期待下文。。。
- [5]蔡津津
- 博主把这些深奥的固体物理讲的这么浅显，太棒了，我这个门外汉看了后也知道一点。博主可以写本固体物理方面的科普书
- 博主回复(2013-7-2 20:07)：谢谢。科普的目的应该是让更多的门外汉看懂。但物理科普做到这点很难，特别是对完全没有理科背景的人……尽力而为吧。
- [4]杜敏彪
- 等电子浓度线
- 博主回复(2013-7-2 20:02)：？？
- [3]王国强
- 所以，金属被称为
具有费米面的固体。
^_^。。。。。。。。。。。。。 - 博主回复(2013-7-2 20:01)：对，金属的费米面是零度时电子真正占据的最高能级，不像半导体，费米能级在能隙中，并不是真正存在的能级。
- [2]王秀锋
- 写得好！期待博主更多的固体物理文章。
费米能级和化学势不一样，费米能级如此文所述是指电子占据的最高能级。
化学势应该是指功函数，即电子完全离开固体原子的静电势（从固体内部到无穷远处）所需要的能量，它应是真空能级和费米能级之差。费米能级越大，化学势越少？
对于一个表面体系，费米能级是一样的，但不同区域的化学势实验测量会不同，是不是因为真空能级不一样所致？ - 博主回复(2013-7-2 19:55)：谢谢
- [1]徐勇刚
- 费米能级和化学势又有啥区别呢？
- 博主回复(2013-7-2 19:55)：我觉得化学势更接近‘费米能’的概念，与真空能量（最低能量态）有关。不过，这几个名词在不同的领域使用时有些混乱，恐怕只有联系上下文才能搞清楚到底说的是什么。我这儿说的是半导体物理中，谈及能带时人们常说的‘费米能级’。并且，在半导体领域，‘费米能级’和‘费米能’是通用的。
1/1 | 总计:
|
No comments:
Post a Comment