http://bzhang.lamost.org/website/archives/power_law_spectrum/
细节因素要独立。看上去有点抽象，其实说的是那些加数-组成事物的要素不能私下暗相沟通，好比如果你认识的女性都私底下串通起来说你很好或很坏，那你约会的人再多也不会取得那个由理想平均数决定的结果。因为所有的女人其实都取得了和你开始约会对象一样的想法。你得到的只是放大的标准差，你第一次约会里的随机性被放大成为一生的结果
高斯与天鹅
本文受到Nassim Nicola Taleb 《黑天鹅》 启示。
我有一个外号叫“理论家”，这可能也是人们对书呆子的戏称，因为我的确非常呆，偏好个从一大堆事物中总结个原理什么。甚至每次和女友打电话后都要来个总结。我精通统计，喜欢求求身边各种事物的平均值，抓住他们的“本质”，而对各种“琐碎”的细节视而不见，认为只要把握事物的总体趋势，就能让我头脑中的“原理”变成生活中的现实，但是现实却教训我是个木讷的傻瓜，甚至会把煮熟的鸭子弄飞。
我老爸没有读过很多书，但他却是个公认的“老狐狸”，在现实生活中往往出奇制胜。他常和我说的一句话是：“胜败在于细节” 。
这让我这个理论家彷徨了，因为细节在我的眼里是是可以漠视的，如同收音机里的噪声。我的信仰来自大名鼎鼎的高斯分布（见下文），那个分布告诉我们，主宰成败的不是个别的细节，而是总体属性。就像我可能因为一次约会没带钱包的经历丢掉女朋友，但是我一生要接触很多女人和进行很多约会，如果我大体还不错，总有一个会成。
但是老爸的话在现实中却屡屡中招。
于是我在思考，我从来都引以为傲的那个由美丽的高斯钟形曲线加上和谐的牛顿定律组成的世界，出了什么问题？
于是我开始钻研生物学，并在“动物世界”里找到了答案，因为一种动物--黑天鹅。
在黑天鹅出现之前，天鹅湖里的天鹅都是雪白，你可以想象那种天蓝色的湖面上飞起千万只白鹅的感觉，远远看去如同乞力马扎罗的雪，于是我以为白是天鹅的标志，我以趋于100%的概率预测天鹅皆白。直到有一天湖面飞过一只纯黑的天鹅，宛如来自世外，它却打碎了我的白天鹅之梦。从此我明白，生物的世界里特例才是本质，而不是平均。 特例总会以比你预想大的概率出现，而把之前的理论打得粉碎。
经典物理的世界是平均数的世界，细节和特例都可以滤掉。但一旦进入生物主导的领域，他们就变成了王道。
![]()
图1：黑天鹅-反叛和破坏性的象征 电影black swan中的那一只演出了它的霸气
在进入肮脏混乱的生物世界前，我们先来悼念一下高斯定律主宰的“白天鹅之舞”。
1.高斯分布与大数定理 平均的力量
我们经常用平均数表达事物的总体状况，如中国男人的身高1米7，对于做统计的人，平均数几乎成为信仰，我们往往已经忘记了这种信仰背后的基本假设-高斯分布，只有在我们统计的事物呈高斯分布，平均数才真正能够代表事物的属性。
预备知识：加和等于平均。 平均数的运算依赖于把很多的数据相加后除以数据的个数。 样本在平均数附近的偏差大小由标准差表示。经典理论告诉我们，样本的容量越大，平均数就越能代表所研究群体。
![]()
图2：高斯吊钟曲线，中间的竖线指代平均数，底下的小横杠标注标准差。
![]()
图3： 严肃的高斯与美丽的正态分布曲线出现在10元马克上。
![]()
图4：高斯钟形曲线是标榜独立理性(也是高斯分布成立的条件) 的万门大学的标志 @万门大学(601533749) @童哲(41893570)
高斯告诉我们加法的威力。 对于一个随机事件，比如赌场里掷筛子，随然每一次取得的结果从一到六完全无法预测，但是如果你投上一万次，把你每次投的点数加起来你却得到一个可以被越来越精确预测的数。这个结果可以被一条称作高斯曲线的东西描述，它具有两个特征量，平均数和标准差. 平均数描述总体趋势而标准差告诉你不确定性的大小。 高斯告诉我们，随着加数的增多，标准差在平均数面前越来越微不足道，直到可以忽略不计，或者说通过无穷加和，一个随机事件成为确定事件，我们越来越精确的得到平均数。 这条法则叫做大数定理（law of large number)。
![]()
图5：大数定律，我们看到随着样本总数N的增加，钟形曲线越来越瘦（对平均数的偏离减小），如过你想象一下N无限大，我们就得到一根竖线--代表我们以任意精度得到平均数，不确定性被消除。
大数定律的威力，在于他使得一个确定性的世界可以在庞大的不确定性之上产生。就好比明天太阳升起春天花儿会开这种事，我们知道不发生的概率几乎为0。其实都是高斯分布和大数定理的保证，因为太阳升花儿开是组成太阳和花儿无数的原子和分子共同作用的结果，一旦沾上“无数”“共同作用” 大数定理就以任意高的精确性保证事物一定会发生。就像即使你有一大堆散漫不靠谱的士兵，你依然可以靠数量赢得战役的胜利。正态分布和大数定理是所有确定性的根源，因为我们的可见世界就是无数不确定的微观因素不断加和的结果。
对于细节重要性的启示：他告诉我们当决定事件的因素足够多，试验的次数足够大，每一件事，微小的细节不再重要，因为它们在巨量的加和中被平均掉了。
不过不要高兴太早。
高斯定律背后的陷阱：
A.细节因素要独立。看上去有点抽象，其实说的是那些加数-组成事物的要素不能私下暗相沟通，好比如果你认识的女性都私底下串通起来说你很好或很坏，那你约会的人再多也不会取得那个由理想平均数决定的结果。因为所有的女人其实都取得了和你开始约会对象一样的想法。你得到的只是放大的标准差，你第一次约会里的随机性被放大成为一生的结果。 初始条件的影响被放大，所谓亚马逊森林的蝴蝶扇扇翅膀，引起大西洋上的一场风暴。
B.时间平移不变形。这个又有点玄了。 简单的例子，如果你投掷的时候筛子被人换掉，变成一个加了机关的筛子，每一面都是一点，而且后面又经常被时不时的换掉，那你永远得不到稳定的平均数，如过你还在那里按高斯定理做加法，指望你会最终赢得平均数给定的钱数，就是被骗的傻瓜。
大数定理是我们认识随机世界的基础，他告诉我们确定性如何从偶然性的基础上浮现。但是他就如同牛顿第一定律和理想气体模型，光滑水平面和无相互作用的基本粒子在真实生物的世界如同幻影般不存在，虽然我们的确在某些时候得到一些趋近的情况。
高斯曲线和大数定律保驾着庄严的理论物理世界，在这里，好好学习就能天天向上，灰姑娘一定会遇到王子。但是，黑天鹅还是摧毁了童话。
黑天鹅效应与幂律分布：
黑天鹅的本质是个体对总体，细节对全局产生决定性影响。 当水面出现一只黑天鹅，整个天鹅群体的属性变化，一个纯白的世界霎时变得中灰。这里当然更多看到特例的影响。
用高斯正态的观点看，黑天鹅出现的概率本来可以忽略，因为我们之前已经统计了巨大的白天鹅样本，但是黑天鹅还是出现了，它的出现似乎没有想的偶然，是我们的运气特别不好吗？ 错。但错的不是你而是正态分布。在生物的世界里，主导的是幂律分布-power law，其实它也正如英文翻译，是一条有关权利和财富的法则（见帕累托分布）。幂律分布的数学表达式简洁无比，不同的幂律分布只体现在幂指数的不同上。它与高斯分布的本质不同在于，高斯正态分布下那些概率小到可忽略的事件，幂律告你他们没有那么稀有。在幂律的观点下，黑天鹅的出现是可以理解的。 罕见的黑天鹅不仅来到，而且决定着全局。
![]()
图4：局部决定整体的象征-Mandelbrot set 所谓分形结构-局部的特征扩算到系统全体-幂律的基础，此处由于篇幅不续，只是提醒同学去看。
![]()
图5：幂律分布与高斯分布的对比，幂律分布最显著的特征是它的长尾，表示那些在高斯分布下的微小概率事件并非那样罕见。
![]()
图6：幂律分布在经济学中的显现-帕累托分布。严重偏离平均值的事件在幂律下不再偶然，并且掌控全局。例如帕累托指出的社会财富的2/8定律，20%的富人掌握80%的财富，这个少数赢家通吃（winner take all）的规律几乎统治着市场经济下的各个领域。还有生态系统里面的大鱼吃小鱼，鱼的尺寸也是幂律分布。它们均体现了在这些体系内元素间存在的全局关联，你我互吃构成的因果链。
为什么黑天鹅影响如此之大? - 在这里现代物理里的相变理论给出了震撼有力的答案。 我在用一个具体的例子点名-雪崩。 雪崩是山顶大面积的雪体坍塌，本来要推到一座雪山是几乎不可能的事情，雪崩符合经典的黑天鹅事件的定义，按常理几乎不会发生，一旦发生即致命。为什么在现实中我们却经常听到雪崩的事故呢？ 因为雪崩的诱因其实与它的影响相反，非常微小, 可能是一粒小石子达到雪山上，或者一个人在喊话，这些诱因没那么罕见。这些微小因素在绝大多数情况下都对雪坡毫无影响，但是在一种情况下却不是-那就是雪体的临界状态，只有在临界状态下雪崩才会发生。
临界状态是一种脆弱的平衡状态，维持雪体凝聚在一起的力量和使雪体瓦解的力量几乎相等，但是只要天平稍微倾斜变万劫不复。你在庞大的雪坡上投一粒微小的石子，石子的作用力不是被局部的雪体吸收而是扩散到整个雪体，如同压死骆驼的最后一颗稻草，使平衡整体倒戈。
临界状态使得黑天鹅成为决定性的力量。
![]()
图7: 雪崩-宏大雪坡瞬间瓦解。
雪崩理论的核心是临界状态下细节的作用的被无限放大（正反馈）。一个本来只限于局部的小因素在临界态下扩散到全身。雪崩的理论遍布各个领域，例如地震，股市崩盘，金融危机，甚至社会革命的爆发。
他甚至蔓延在我们的生活中，如两个队伍拔河，两边开始势均力敌，但是其中某个人因为口袋里的手机响，疑为女友打来电话而懈怠的一瞬间导致了整个输赢力量的微小偏移，但因为本来势均力敌，所以个体微小的作用被放大，而这一效应又导致慌张情绪在全队的蔓延，结果由于一个手机铃响而毁掉了一场比赛。所谓丢失一个钉子，坏了一只蹄铁, 坏了一只蹄铁，折了一匹战马，折了一匹战马，伤了一位骑士, 伤了一位骑士，输了一场战斗, 输了一场战斗，亡了一个帝国。 如果一批战马恰好坏在关键战局而且双方力量难分胜负，就会毁掉一个帝国。这点也是为什么越是势均力敌的高手比赛，越要拼运气。
生命洪流的本质是一种特殊的相变。因此跟生物有关的事情，包括生物的历史和我们人类的历史和我们每个人的一生，都发生在临界状态，那个充满着大大小小的雪崩的状态，那个不可预见的细节决定全局的状态。既然你明天还活着，黑天鹅就会起飞。 归根溯源，生命的产生，进化，到我们的出生，都是一系列黑天鹅起飞的结果，我们本身就是黑天鹅，又何必惧怕明天它再次划过你的窗前。
黑天鹅把不确定性深刻的带入我们的日常生活，作为理论家的我，感到那个充满着完美的直线，抛物线，和牛顿定律的世界犹如一座空城，如盗梦空间里那座无人的死城。它庞大的钢筋水泥，依然支撑着现代工业，甚至引领我们发现黑天鹅的秘密，却无法让我们了解我们自身。
![]()
图0：黑天鹅触发了我世界观的雪崩，如同inception里梦幻之城坍塌的情景。
注：生物进化是最原汁原味的黑天鹅效应，生物的变异本来已经是特例，而能够幸存的变异更是特例之特例，正是这样的特例而非主流（平均数）主导了生物的演化。我们统治世界的哺乳类的祖先，曾在亿万年里躲在当时的主流爬行类（恐龙）的阴影下吃着它们掉下的残渣生活，直到有一天，黑天鹅降临--一场天灾结束了爬行类的霸主地位.....
启示：
对待机遇： 活下去是硬道理。我们的文化鼓励英雄，其实历史是幸存者写下的。好好活，心胸开阔，眼界放开，积极准备，你就有更多的机会等到你的黑天鹅。
风险预测： 黑天鹅的特点就是黑，它在出现之前躲在暗处，即使它就在你背后注视着你，你还是无法知道。 想到这里我反而不担心。因为那些已知的所谓风险都不险，真正的风险你也没法知道。
风险控制：止损。当负面的黑天鹅降临的时候，唯一能做的是把它的影响限制在局部而不致于引发雪崩。
对待细节： 决定成败的细节是无法事先预测的。因此我认为把视线锁定在狭小范围是不明智的，因为你大脑能够关注的细节数有限，而黑天鹅出现的方位无法预测。你能做的其实只是深呼吸，盯住当下。
不要迷恋于相信格言： 格言代表的是大数定理下的平均，而格言适用的范围往往不适用高斯分布（大数定理不成立）。而且又一次，格言是幸存者写下的，死去的人不说话。
对待学术： 依然不要轻视高斯，因为即使是幂律分布，也只有懂得了高斯才明白它的价值。
我有一个外号叫“理论家”，这可能也是人们对书呆子的戏称，因为我的确非常呆，偏好个从一大堆事物中总结个原理什么。甚至每次和女友打电话后都要来个总结。我精通统计，喜欢求求身边各种事物的平均值，抓住他们的“本质”，而对各种“琐碎”的细节视而不见，认为只要把握事物的总体趋势，就能让我头脑中的“原理”变成生活中的现实，但是现实却教训我是个木讷的傻瓜，甚至会把煮熟的鸭子弄飞。
我老爸没有读过很多书，但他却是个公认的“老狐狸”，在现实生活中往往出奇制胜。他常和我说的一句话是：“胜败在于细节” 。
这让我这个理论家彷徨了，因为细节在我的眼里是是可以漠视的，如同收音机里的噪声。我的信仰来自大名鼎鼎的高斯分布（见下文），那个分布告诉我们，主宰成败的不是个别的细节，而是总体属性。就像我可能因为一次约会没带钱包的经历丢掉女朋友，但是我一生要接触很多女人和进行很多约会，如果我大体还不错，总有一个会成。
但是老爸的话在现实中却屡屡中招。
于是我在思考，我从来都引以为傲的那个由美丽的高斯钟形曲线加上和谐的牛顿定律组成的世界，出了什么问题？
于是我开始钻研生物学，并在“动物世界”里找到了答案，因为一种动物--黑天鹅。
在黑天鹅出现之前，天鹅湖里的天鹅都是雪白，你可以想象那种天蓝色的湖面上飞起千万只白鹅的感觉，远远看去如同乞力马扎罗的雪，于是我以为白是天鹅的标志，我以趋于100%的概率预测天鹅皆白。直到有一天湖面飞过一只纯黑的天鹅，宛如来自世外，它却打碎了我的白天鹅之梦。从此我明白，生物的世界里特例才是本质，而不是平均。 特例总会以比你预想大的概率出现，而把之前的理论打得粉碎。
经典物理的世界是平均数的世界，细节和特例都可以滤掉。但一旦进入生物主导的领域，他们就变成了王道。
图1：黑天鹅-反叛和破坏性的象征 电影black swan中的那一只演出了它的霸气
在进入肮脏混乱的生物世界前，我们先来悼念一下高斯定律主宰的“白天鹅之舞”。
1.高斯分布与大数定理 平均的力量
我们经常用平均数表达事物的总体状况，如中国男人的身高1米7，对于做统计的人，平均数几乎成为信仰，我们往往已经忘记了这种信仰背后的基本假设-高斯分布，只有在我们统计的事物呈高斯分布，平均数才真正能够代表事物的属性。
预备知识：加和等于平均。 平均数的运算依赖于把很多的数据相加后除以数据的个数。 样本在平均数附近的偏差大小由标准差表示。经典理论告诉我们，样本的容量越大，平均数就越能代表所研究群体。
图2：高斯吊钟曲线，中间的竖线指代平均数，底下的小横杠标注标准差。
图3： 严肃的高斯与美丽的正态分布曲线出现在10元马克上。
图4：高斯钟形曲线是标榜独立理性(也是高斯分布成立的条件) 的万门大学的标志 @万门大学(601533749) @童哲(41893570)
高斯告诉我们加法的威力。 对于一个随机事件，比如赌场里掷筛子，随然每一次取得的结果从一到六完全无法预测，但是如果你投上一万次，把你每次投的点数加起来你却得到一个可以被越来越精确预测的数。这个结果可以被一条称作高斯曲线的东西描述，它具有两个特征量，平均数和标准差. 平均数描述总体趋势而标准差告诉你不确定性的大小。 高斯告诉我们，随着加数的增多，标准差在平均数面前越来越微不足道，直到可以忽略不计，或者说通过无穷加和，一个随机事件成为确定事件，我们越来越精确的得到平均数。 这条法则叫做大数定理（law of large number)。
图5：大数定律，我们看到随着样本总数N的增加，钟形曲线越来越瘦（对平均数的偏离减小），如过你想象一下N无限大，我们就得到一根竖线--代表我们以任意精度得到平均数，不确定性被消除。
大数定律的威力，在于他使得一个确定性的世界可以在庞大的不确定性之上产生。就好比明天太阳升起春天花儿会开这种事，我们知道不发生的概率几乎为0。其实都是高斯分布和大数定理的保证，因为太阳升花儿开是组成太阳和花儿无数的原子和分子共同作用的结果，一旦沾上“无数”“共同作用” 大数定理就以任意高的精确性保证事物一定会发生。就像即使你有一大堆散漫不靠谱的士兵，你依然可以靠数量赢得战役的胜利。正态分布和大数定理是所有确定性的根源，因为我们的可见世界就是无数不确定的微观因素不断加和的结果。
对于细节重要性的启示：他告诉我们当决定事件的因素足够多，试验的次数足够大，每一件事，微小的细节不再重要，因为它们在巨量的加和中被平均掉了。
不过不要高兴太早。
高斯定律背后的陷阱：
A.细节因素要独立。看上去有点抽象，其实说的是那些加数-组成事物的要素不能私下暗相沟通，好比如果你认识的女性都私底下串通起来说你很好或很坏，那你约会的人再多也不会取得那个由理想平均数决定的结果。因为所有的女人其实都取得了和你开始约会对象一样的想法。你得到的只是放大的标准差，你第一次约会里的随机性被放大成为一生的结果。 初始条件的影响被放大，所谓亚马逊森林的蝴蝶扇扇翅膀，引起大西洋上的一场风暴。
B.时间平移不变形。这个又有点玄了。 简单的例子，如果你投掷的时候筛子被人换掉，变成一个加了机关的筛子，每一面都是一点，而且后面又经常被时不时的换掉，那你永远得不到稳定的平均数，如过你还在那里按高斯定理做加法，指望你会最终赢得平均数给定的钱数，就是被骗的傻瓜。
大数定理是我们认识随机世界的基础，他告诉我们确定性如何从偶然性的基础上浮现。但是他就如同牛顿第一定律和理想气体模型，光滑水平面和无相互作用的基本粒子在真实生物的世界如同幻影般不存在，虽然我们的确在某些时候得到一些趋近的情况。
高斯曲线和大数定律保驾着庄严的理论物理世界，在这里，好好学习就能天天向上，灰姑娘一定会遇到王子。但是，黑天鹅还是摧毁了童话。
黑天鹅效应与幂律分布：
黑天鹅的本质是个体对总体，细节对全局产生决定性影响。 当水面出现一只黑天鹅，整个天鹅群体的属性变化，一个纯白的世界霎时变得中灰。这里当然更多看到特例的影响。
用高斯正态的观点看，黑天鹅出现的概率本来可以忽略，因为我们之前已经统计了巨大的白天鹅样本，但是黑天鹅还是出现了，它的出现似乎没有想的偶然，是我们的运气特别不好吗？ 错。但错的不是你而是正态分布。在生物的世界里，主导的是幂律分布-power law，其实它也正如英文翻译，是一条有关权利和财富的法则（见帕累托分布）。幂律分布的数学表达式简洁无比，不同的幂律分布只体现在幂指数的不同上。它与高斯分布的本质不同在于，高斯正态分布下那些概率小到可忽略的事件，幂律告你他们没有那么稀有。在幂律的观点下，黑天鹅的出现是可以理解的。 罕见的黑天鹅不仅来到，而且决定着全局。
图4：局部决定整体的象征-Mandelbrot set 所谓分形结构-局部的特征扩算到系统全体-幂律的基础，此处由于篇幅不续，只是提醒同学去看。
图5：幂律分布与高斯分布的对比，幂律分布最显著的特征是它的长尾，表示那些在高斯分布下的微小概率事件并非那样罕见。
图6：幂律分布在经济学中的显现-帕累托分布。严重偏离平均值的事件在幂律下不再偶然，并且掌控全局。例如帕累托指出的社会财富的2/8定律，20%的富人掌握80%的财富，这个少数赢家通吃（winner take all）的规律几乎统治着市场经济下的各个领域。还有生态系统里面的大鱼吃小鱼，鱼的尺寸也是幂律分布。它们均体现了在这些体系内元素间存在的全局关联，你我互吃构成的因果链。
为什么黑天鹅影响如此之大? - 在这里现代物理里的相变理论给出了震撼有力的答案。 我在用一个具体的例子点名-雪崩。 雪崩是山顶大面积的雪体坍塌，本来要推到一座雪山是几乎不可能的事情，雪崩符合经典的黑天鹅事件的定义，按常理几乎不会发生，一旦发生即致命。为什么在现实中我们却经常听到雪崩的事故呢？ 因为雪崩的诱因其实与它的影响相反，非常微小, 可能是一粒小石子达到雪山上，或者一个人在喊话，这些诱因没那么罕见。这些微小因素在绝大多数情况下都对雪坡毫无影响，但是在一种情况下却不是-那就是雪体的临界状态，只有在临界状态下雪崩才会发生。
临界状态是一种脆弱的平衡状态，维持雪体凝聚在一起的力量和使雪体瓦解的力量几乎相等，但是只要天平稍微倾斜变万劫不复。你在庞大的雪坡上投一粒微小的石子，石子的作用力不是被局部的雪体吸收而是扩散到整个雪体，如同压死骆驼的最后一颗稻草，使平衡整体倒戈。
临界状态使得黑天鹅成为决定性的力量。
图7: 雪崩-宏大雪坡瞬间瓦解。
雪崩理论的核心是临界状态下细节的作用的被无限放大（正反馈）。一个本来只限于局部的小因素在临界态下扩散到全身。雪崩的理论遍布各个领域，例如地震，股市崩盘，金融危机，甚至社会革命的爆发。
他甚至蔓延在我们的生活中，如两个队伍拔河，两边开始势均力敌，但是其中某个人因为口袋里的手机响，疑为女友打来电话而懈怠的一瞬间导致了整个输赢力量的微小偏移，但因为本来势均力敌，所以个体微小的作用被放大，而这一效应又导致慌张情绪在全队的蔓延，结果由于一个手机铃响而毁掉了一场比赛。所谓丢失一个钉子，坏了一只蹄铁, 坏了一只蹄铁，折了一匹战马，折了一匹战马，伤了一位骑士, 伤了一位骑士，输了一场战斗, 输了一场战斗，亡了一个帝国。 如果一批战马恰好坏在关键战局而且双方力量难分胜负，就会毁掉一个帝国。这点也是为什么越是势均力敌的高手比赛，越要拼运气。
生命洪流的本质是一种特殊的相变。因此跟生物有关的事情，包括生物的历史和我们人类的历史和我们每个人的一生，都发生在临界状态，那个充满着大大小小的雪崩的状态，那个不可预见的细节决定全局的状态。既然你明天还活着，黑天鹅就会起飞。 归根溯源，生命的产生，进化，到我们的出生，都是一系列黑天鹅起飞的结果，我们本身就是黑天鹅，又何必惧怕明天它再次划过你的窗前。
黑天鹅把不确定性深刻的带入我们的日常生活，作为理论家的我，感到那个充满着完美的直线，抛物线，和牛顿定律的世界犹如一座空城，如盗梦空间里那座无人的死城。它庞大的钢筋水泥，依然支撑着现代工业，甚至引领我们发现黑天鹅的秘密，却无法让我们了解我们自身。
图0：黑天鹅触发了我世界观的雪崩，如同inception里梦幻之城坍塌的情景。
注：生物进化是最原汁原味的黑天鹅效应，生物的变异本来已经是特例，而能够幸存的变异更是特例之特例，正是这样的特例而非主流（平均数）主导了生物的演化。我们统治世界的哺乳类的祖先，曾在亿万年里躲在当时的主流爬行类（恐龙）的阴影下吃着它们掉下的残渣生活，直到有一天，黑天鹅降临--一场天灾结束了爬行类的霸主地位.....
启示：
对待机遇： 活下去是硬道理。我们的文化鼓励英雄，其实历史是幸存者写下的。好好活，心胸开阔，眼界放开，积极准备，你就有更多的机会等到你的黑天鹅。
风险预测： 黑天鹅的特点就是黑，它在出现之前躲在暗处，即使它就在你背后注视着你，你还是无法知道。 想到这里我反而不担心。因为那些已知的所谓风险都不险，真正的风险你也没法知道。
风险控制：止损。当负面的黑天鹅降临的时候，唯一能做的是把它的影响限制在局部而不致于引发雪崩。
对待细节： 决定成败的细节是无法事先预测的。因此我认为把视线锁定在狭小范围是不明智的，因为你大脑能够关注的细节数有限，而黑天鹅出现的方位无法预测。你能做的其实只是深呼吸，盯住当下。
不要迷恋于相信格言： 格言代表的是大数定理下的平均，而格言适用的范围往往不适用高斯分布（大数定理不成立）。而且又一次，格言是幸存者写下的，死去的人不说话。
对待学术： 依然不要轻视高斯，因为即使是幂律分布，也只有懂得了高斯才明白它的价值。
说说幂律谱的问题
在天文学中，幂律谱可以说是再常见不过了。非热辐射、宇宙线粒子能量分布，甚至还有陨星的质量分布，通通可以用幂律谱来描述。一般在统计工作中，也往往采用幂律形式来描述两个量之间的关系。由于本人正在计算非热辐射，最近基本上是每天都要与幂律谱打交道。
幂律谱的表示形式很简单，只是以下式子：
 \propto x^{-\alpha})
其中的
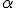唤作谱指数。其几何意义就是在对数坐标图上，谱的斜率为
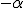。谱拟合也很简单，原则上说只要给定两点的
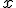与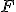
就可以做到。当然在实际操作中，由于测量误差等因素的存在，往往用的是多点拟合的方式。
当然从表达式来看，幂律就是个非常普遍的存在，线性关系可以看作是其中的一个特例。而人们熟知的平方反比定律也可以算作是幂律关系，描述黑体辐射能流密度与温度联系的斯忒藩—玻尔兹曼定律亦是如此。
天体物理学中，在电磁波谱的两端，幂律谱都在大唱主角，比如用于描述伽玛暴的Band双幂律谱，还有超新星遗迹在射电波段的辐射形式。对于后者，谱指数往往还是遗迹分类的重要因素：依靠中心致密天体供能的实心型往往谱指数偏小，作为激波产物的壳层型则偏大。
要说这幂律谱形的起源，首先要说说带电粒子能量（因此也就是洛伦兹因子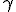
，因能量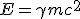
）的幂律分布。这样的粒子是加速的产物，常见的加速机制包括激波的一阶加速、磁场中的二阶费米加速等等，这里的阶数是针对能量的改变与粒子同加速区相对速度之间的关系而言的，一阶加速的效率要更高一些。
设每次加速后粒子的能量就增加到原先的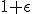
倍，同时有
的概率继续停留在加速区被进一步加速。那么它就有^n)
的概率来接受n次加速，而加速后粒子能量是原先的^n)
倍。由此得到的粒子集体能量分布就是幂律形式的，而且在
与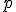
不太大的情况下，还可以导出幂律指数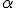近似满足
。
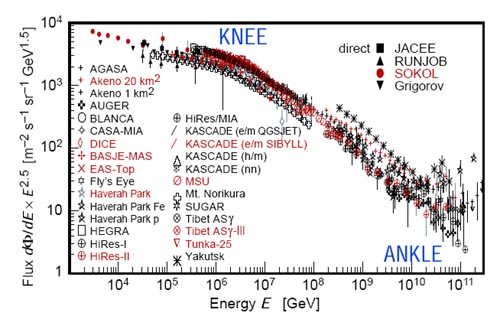
不同的指数意味着不同的加速机制。典型的例子就是初级宇宙线的能谱：
对于非热辐射机制，在天体物理学环境下一般是同步加速辐射与逆康普顿散射。将幂律分布的电子代入辐射的表达式，自然就可以给出幂律形式的谱形，而且对于同步加速辐射来说，若不考虑同步自吸收与冷却效应，电子的幂律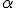指数与谱指数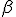
之间就应该有
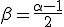的联系。当然如果冷却或者自吸收存在，问题要复杂许多。就算不考虑这些，很多精细的数值模型给出的激波加速电子谱分布往往也偏离单纯的幂律，因此实际的辐射谱会更加复杂。
至于其他呈幂律形态的统计关系，各自有各自的原因，如旋涡星系的Tully-Fisher关系可以用运动来解释，而椭圆星系的Faber-Jackson关系则可以归结为位力定理。描述伽玛暴的数种统计关系往往认为是同步辐射所致，对于流星体的质量分布，甚至还有说法认为是由于间接测量导致的假象。
幂律谱的表示形式很简单，只是以下式子：
当然从表达式来看，幂律就是个非常普遍的存在，线性关系可以看作是其中的一个特例。而人们熟知的平方反比定律也可以算作是幂律关系，描述黑体辐射能流密度与温度联系的斯忒藩—玻尔兹曼定律亦是如此。
天体物理学中，在电磁波谱的两端，幂律谱都在大唱主角，比如用于描述伽玛暴的Band双幂律谱，还有超新星遗迹在射电波段的辐射形式。对于后者，谱指数往往还是遗迹分类的重要因素：依靠中心致密天体供能的实心型往往谱指数偏小，作为激波产物的壳层型则偏大。
要说这幂律谱形的起源，首先要说说带电粒子能量（因此也就是洛伦兹因子
设每次加速后粒子的能量就增加到原先的
不同的指数意味着不同的加速机制。典型的例子就是初级宇宙线的能谱：
Hoerandel 2003
图中分别位于106与1010 GeV的两个拐点叫做“Knee”与“Ankle”，后者标志着河外起源的高能带电粒子，一般认为它们往往由活动星系核或是致密星双星系统加速。而关于前者的成因有多种说法，包括高能粒子从银河系中的逃逸，或者是达到超新星加速上限后，新的加速机制起了主导作用。对于非热辐射机制，在天体物理学环境下一般是同步加速辐射与逆康普顿散射。将幂律分布的电子代入辐射的表达式，自然就可以给出幂律形式的谱形，而且对于同步加速辐射来说，若不考虑同步自吸收与冷却效应，电子的幂律指数
至于其他呈幂律形态的统计关系，各自有各自的原因，如旋涡星系的Tully-Fisher关系可以用运动来解释，而椭圆星系的Faber-Jackson关系则可以归结为位力定理。描述伽玛暴的数种统计关系往往认为是同步辐射所致，对于流星体的质量分布，甚至还有说法认为是由于间接测量导致的假象。
No comments:
Post a Comment