马赫数,也称“马氏数”、“M-数”,因奥地利物理学家马赫而得名。飞行器在空气中的运动速度与该高度远前方未受扰动的空气中的音速的比值,称飞行马赫数。
雷诺数[编辑]
维基百科,自由的百科全书
流体力学中,雷诺数(Reynolds number)是流体惯性力 与黏性力
与黏性力 比值的量度,它是一个无量纲量。
比值的量度,它是一个无量纲量。
雷諾數較小時,黏滯力對流場的影響大於慣性力,流場中流速的擾動會因黏滯力而衰減,流體流動穩定,為層流;反之,若雷諾數較大時,慣性力對流場的影響大於黏滯力,流體流動較不穩定,流速的微小變化容易發展、增強,形成紊亂、不規則的紊流流場。
假如雷諾數的體積流速固定,則雷諾數與密度(ρ)、速度的开方( )成正比;與管徑(D)和黏度(u)成反比
)成正比;與管徑(D)和黏度(u)成反比
假如雷諾數的質量流速(即是可以穩定流動)固定,則雷諾數與管徑(D)、黏度(u)成反比;與√速度( )成正比;與密度(ρ)無關
)成正比;與密度(ρ)無關
 , 这里x是从平板的前边缘开始的距离,流速是边界层以外的自由流场速度。
, 这里x是从平板的前边缘开始的距离,流速是边界层以外的自由流场速度。
一般管道流雷诺数<2100为层流(又可稱作黏滯流動、線流)状态,大于4000为湍流(又可稱作紊流、擾流)状态,2100~4000为过渡流状态。
層流:流體沿著管軸以平行方向流動,因為流體很平穩,所以可看作層層相疊,各層間不互相干擾。流體在管內速度分佈為拋物體的形狀,面向切面的則是拋物線分佈。因為是個別有其方向和速率流動,所以流動摩擦損失較小。
湍流:此則是管內流體流動狀態為各分子互相激烈碰撞,非直線流動而是漩渦狀,流動摩擦損失較大。
在管道中完全成形(fully developed)流體的壓降可以用穆迪圖來說明,穆迪圖繪製出在不同相對粗糙度下,達西摩擦因子f和雷诺数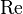 及相對粗糙度
及相對粗糙度 的關係,圖中隨著雷诺数的增加,管流由層流變為过渡流及湍流,管流的特性和流體為层流、过渡流或湍流有明顯關係。
的關係,圖中隨著雷诺数的增加,管流由層流變為过渡流及湍流,管流的特性和流體為层流、过渡流或湍流有明顯關係。
雷诺数的一般值
湍流临界值~ 2.3×103-5.0×104(对于管内流)到106(边界层)

最后,为了阅读方便把撇去掉:
 与黏性力
与黏性力 比值的量度,它是一个无量纲量。
比值的量度,它是一个无量纲量。雷諾數較小時,黏滯力對流場的影響大於慣性力,流場中流速的擾動會因黏滯力而衰減,流體流動穩定,為層流;反之,若雷諾數較大時,慣性力對流場的影響大於黏滯力,流體流動較不穩定,流速的微小變化容易發展、增強,形成紊亂、不規則的紊流流場。
目录
[隐藏]定义[编辑]
对于不同的流场,雷诺数可以有很多表达方式。这些表达方式一般都包括流体性质(密度、黏度)再加上流体速度和一个特征长度或者特征尺寸。这个尺寸一般是根据习惯定义的。比如说半径和直径对于球型和圆形并没有本质不同,但是习惯上只用其中一个。对于管内流动和在流场中的球体,通常使用直径作为特征尺寸。对于表面流动,通常使用长度。管内流场[编辑]
对于在管内的流动,雷诺数定义为:假如雷諾數的體積流速固定,則雷諾數與密度(ρ)、速度的开方(
 )成正比;與管徑(D)和黏度(u)成反比
)成正比;與管徑(D)和黏度(u)成反比假如雷諾數的質量流速(即是可以穩定流動)固定,則雷諾數與管徑(D)、黏度(u)成反比;與√速度(
 )成正比;與密度(ρ)無關
)成正比;與密度(ρ)無關平板流[编辑]
对于在两个宽板(板宽远大于两板之间距离)之间的流动,特征长度为两倍的两板之间距离。流体中的物体[编辑]
对于流体中的物体的雷诺数,经常用Rep表示。用雷诺数可以研究物体周围的流动情况,是否有漩涡分离,还可以研究沉降速度。流体中的球[编辑]
对于在流体中的球,特征长度就是这个球的直径,特征速度是这个球相对于远处流体的速度,密度和黏度都是流体的性质。在这种情况下,层流只存在于Re=0.1或者以下。 在小雷诺数情况下,力和运动速度的关系遵从斯托克斯定律。搅拌槽[编辑]
对于一个圆柱形的搅拌槽,中间有一个旋转的桨或者涡轮,特征长度是这个旋转物体的直径。速度是ND,N是转速(周/秒)。雷诺数表达为:过渡流雷诺数[编辑]
对于流过平板的边界层,实验可以确认,当流过一定长度后,层流变得不稳定形成湍流。对于不同的尺度和不同的流体,这种不稳定性都会发生。一般来说,当 , 这里x是从平板的前边缘开始的距离,流速是边界层以外的自由流场速度。
, 这里x是从平板的前边缘开始的距离,流速是边界层以外的自由流场速度。一般管道流雷诺数<2100为层流(又可稱作黏滯流動、線流)状态,大于4000为湍流(又可稱作紊流、擾流)状态,2100~4000为过渡流状态。
層流:流體沿著管軸以平行方向流動,因為流體很平穩,所以可看作層層相疊,各層間不互相干擾。流體在管內速度分佈為拋物體的形狀,面向切面的則是拋物線分佈。因為是個別有其方向和速率流動,所以流動摩擦損失較小。
湍流:此則是管內流體流動狀態為各分子互相激烈碰撞,非直線流動而是漩渦狀,流動摩擦損失較大。
管道中的摩擦阻力[编辑]
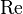 及相對粗糙度
及相對粗糙度 的關係,圖中隨著雷诺数的增加,管流由層流變為过渡流及湍流,管流的特性和流體為层流、过渡流或湍流有明顯關係。
的關係,圖中隨著雷诺数的增加,管流由層流變為过渡流及湍流,管流的特性和流體為层流、过渡流或湍流有明顯關係。流动相似性[编辑]
两个流动如果相似的话,他们必须有相同的几何形状和相同的雷诺数和欧拉数。当在模型和真实的流动之间比较两个流体中相应的一点,如下关系式成立:雷诺数的一般值
湍流临界值~ 2.3×103-5.0×104(对于管内流)到106(边界层)
雷诺数的推导[编辑]
雷诺数可以从无量纲的非可压納維-斯托克斯方程推导得来:
最后,为了阅读方便把撇去掉:
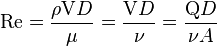
 是平均流速(
是平均流速( 管直径(一般為特徵長度)(m)
管直径(一般為特徵長度)(m) 流体
流体
 ρ)(m²/s)
ρ)(m²/s)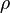 流体
流体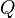 体积
体积 横截面积(m²)
横截面积(m²)







No comments:
Post a Comment