Sunday, February 15, 2015

微分方程的解，滿足疊加原理（或稱線性條件） 传统的纯各向异性扩散模型（一阶导数，用梯度表示）在平滑区域过度扩散，产生“阶梯效应”.

微分方程的解，滿足疊加原理（或稱線性條件）
[PDF]全文查看 - 中北大学出版中心
xuebao.nuc.edu.cn/wz/pdf/xbzr/2011/.../zr2011-4-512.pdf
轉為繁體網頁
由 杨迎春 著作 - ‎2011 - ‎被引用 2 次 - ‎相關文章
摘要： 针对传统的纯各向异性扩散模型（一阶导数，用梯度表示）在平滑区域过度扩散，产生“阶梯效应”. 和四阶PDE（PartialDifferentialEquations）模型（二阶导数， ...

 
微分方程

Differential Equation		 

  十七世紀後，自然科學與技術蓬勃的發展，一個核心的因素是微積分的發明，而微積分之所以能廣泛地應用在各科學課題，則是因為這些問題經常被化歸為解某微分方程的問題。因此，微分方程成為整個十八與十九世紀數學發展的主調，其中包括各種重要微分方程解的研究，求解方法的發展，一般理論的萌芽，在經由反饋而催生新的數學領域。
例子
底下是一些微分方程的例子
(1) $\frac{dy(x)}{dx}=x$
(2) Malthus人口方程：

\begin{displaymath}\frac{dP(t)}{dt}=\lambda P(t),\lambda\in R \end{displaymath}


(3) 虎克定律：

\begin{displaymath}\frac{d^2y}{dx^2}=-\kappa y \end{displaymath}


(4) 牛頓萬有引力方程

\begin{displaymath} \overrightarrow{X}''=-C\cdot\frac{\overrightarrow{X}}{\vert\vert\overrightarrow{X}\vert\vert^3} \end{displaymath}


其中 $\overrightarrow{X}(t) = (x(t),y(t),z(t))$, $\vert\vert\overrightarrow{X}(t)\vert\vert^2=x^2(t)+y^2(t)+z^2(t)$, $\overrightarrow{X}$ 代表相對的位置向量，例如行星之於太陽。
(5) d'Alembert 波動方程：

\begin{displaymath}\frac{\partial y(x,t)}{\partial x^2}=c^2\frac{\partial y(x,t)}{\partial t^2}\end{displaymath}


(6) 勢方程或 Laplace 方程：

\begin{displaymath}\Delta V\equiv\frac{\partial^2V}{\partial x^2}+\frac{\partial^2V}{\partial y^2}+\frac{\partial^2V}{\partial z^2}=0\end{displaymath}


其中 V(x,y,z) 為空間位置函數。
(7) Fourier 熱傳導方程：

\begin{displaymath}\frac{\partial T}{\partial t}=\frac{1}{\kappa^2}\Delta T\end{displaymath}


$\Delta=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}$,T(x,y,t) 溫度函數。
(8) Largrange 最小曲面方程：

(1+q2)r-2pqs+(1+p2)t=0


其中 z=z(x,y) 為曲面之函數式， $p\equiv\frac{\partial z}{\partial x}$, $q\equiv\frac{\partial z}{\partial y}$, $r\equiv\frac{\partial^2 z}{\partial x^2}$, $s\equiv\frac{\partial^2 z}{\partial x\partial y}$, $t\equiv\frac{\partial^2 z}{\partial y^2}$。
(9)Maxwell 方程式：

\begin{displaymath} \left\{ \begin{array}{lll} \mbox{curl} H&=&\frac{1}{c}\fra... ...\epsilon E)&=&\rho\\ \mbox{div}(\mu H)&=&0 \end{array}\right. \end{displaymath}


由這些例子，我們知道微分方程就是指一些函數的方程式或方程組，而且式中還包括了這些函數的導函數或偏導函數。 		 
對外搜尋關鍵字：
．Malthus人口方程
．萬有引力方程
．波動方程
．Laplace方程
．熱傳導方程
．最小曲面方程
．Maxwell方程式
．常微分方程
．偏微分方程
．線性條件
．Huygens
．Leibniz
．James Bernoulli
．等時曲線
．簡諧運動
．d'Alembert
．Euler
．Danial Bernoulli
．函數
．Fourier級數
．Kepler
．行星運動定律
．Laplace
．Lagrange
．Poincare
．愛因斯坦
．測地線
．變分學
．最小作用原理
．微積分基本定理
．線性代數
．特殊函數
．Bessel函數
．Legendre函數
．歐拉法

 
微分方程的一些基本分類
如果在方程式中，我們關心的函數都是某單一變數的函數（例如(1)、(2)、(3)、(4)），則稱為常微分方程（ODE, ordinary differential equation，在物理系統中最常見的變數是時間 t）；不然稱為偏微分方程（PDE, partial differential equation）；如果方程式不只一個，則通稱為微分方程組（例如(4)、(9)）；一個滿足微分方程的函數稱為一個解，通常微分方程的解並不唯一，經常要給定恰當的起始條件才能確定：如果微分方程的解，滿足疊加原理（或稱線性條件）
若 F(x),G(x) 為解，則 $\alpha F(x)+\beta G(x)$ 也是解， $\alpha,\beta \in \mathbf{R}$
則稱為線性方程，（如(1)、(2)、(3)、(5)、(6)、(7)），不然則稱為非線性方程（(4)、(8)），線性常微分方程組，數學家已經非常了解它們的性質，線性偏微分方程也有許多研究，但是非線性則相對地要困難許多。 		  

 
歷史
最早談及微分方程的數學家是 Huygens 與 Leibniz，最先以微積分技巧處理微分方程可能是 James Bernoulli 的等時曲線問題（牛頓的方法是幾何的），但是在早期分析史上最重要的兩個問題來源是
(1) 弦震動問題：
它在與 ODE 的簡諧運動方程或波型方程（形如(3)）有關，在 PDE 則是波動方程。弦震動問題並引發 d'Alembert、Euler、Danial Bernoulli 關於作為起始條件的弦函數可以具有什麼性質的論戰。這次爭論最起碼有兩個意義： (一)它讓數學家意識到非解析函數的重要，並省思函數一詞的意義（見函數）。 (二)藉由 D. Bernoulli 猜測弦函數可以表成無窮三角級數和，開啟後來所謂 Fourier 級數大門（見Fourier）。
(2) n 體問題：
由牛頓重力定律，探討 n 個星球彼此的作用歷程，就是天體力學中的 n 體問題。當 n=2 時，牛頓已充分解出，並推導出 Kepler 的行星運動定律（參看行星運動三大定律)，$n \geq 3$ 的問題沒有一般解，因此刺激了一系列天體問題的研究，Euler、Laplace、Lagrange 都有重要的貢獻，到了十九世紀末，經由 Poincaré 的新觀點，開始微分方程的定性研究，並開啟所謂動力系統的領域（渾沌即為其中一支）。另外由於考慮星球總引力，也導出了所謂的 Laplace 方程（即(6)），相同的想法也出現在電磁學中。
有意義而且影響深遠的微分方程來源，主要是物理與幾何，除了前面所列舉的方程外，舉例來說還有，Euler 以及 Navier-Stokes 的流體力學方程，愛因斯坦廣義相對論的愛因斯坦方程，量子力學中的 Schördinger 方程，Dirac 方程，幾何上的測地線方程，最小曲面（子流形）方程等等。 相當多的微分方程都可以用一種系統性的看法來推導出來，這就是稱為函數空間「微積分學」的變分學（加上最小作用原理）。另外在解決 PDE 問題時可以利用對稱性，分離變數，將問題化歸為 ODE 的問題。 		  

 
方法
解決 ODE 的最基本方法是微積分基本定理，例(1)是顯然的，例(2)可以經由分離變數，變成

\begin{displaymath} (\ln P)'=\lambda t\quad\Rightarrow\quad P=c\cdot e^{\lambda t} \end{displaymath}


n 階線性微分方程組的求解，藉由線性代數與特徵方程式原則上可以說是清楚了。但是要求「確解」，即使是例(1)這種類型的方程也力有未逮，例如 $\frac{dy}{dx}=\sin^2x$。 解決這個問題的方法，首先可能是重新定義所謂的特殊函數 (special function)，例如Bessel 函數，Legendre 函數，以及採用無窮級數法。而 PDE 的問題通常就更困難了。 因此後來在所謂的求解意義上發生了兩類轉折
(1) 所謂存在性（或加上唯一性）的解決方式，論證在某些特定的條件下，解一定會存在，但是通常並不知道解真正的模樣，在 ODE 最基本的是下述定理：
存在唯一性定理. 如果 f(t,y) 在 (t0,y0) 上連續，則一階微分方程

\begin{displaymath} \left\{ \begin{array}{l} y'(t) \;=\; f(t, y(t)) \\ y(t_0)\;=\; y_0 \end{array}\right. \end{displaymath}


有解且僅有一解。
在 PDE 則有 Cauchy-Kovalevskaya 存在性定理。由於存在性定理的需求，也促進泛函分析的發展（當然另一個來源是量子力學）。
(2) 另外則是採用數值計算的方式，在已知解存在的情形下，以最有效率的方式，來求近似解，最簡單的例子是 ODE 中的歐拉法。由於廿世紀中期之後電子計算機的發達，運用數值方法來求微分方程的解，已經是一們相當專門的學科。
  

 （撰稿：翁秉仁∕台大數學系）

相關網頁：
數學與科學：行星運動三大定律（曹亮吉）
數學與科學：生態學之 Lokta-Volterra 模型（翁秉仁）
數學與科學：傳染病之擴散模型（翁秉仁）
數學與科學：人口成長模型（翁秉仁）


回頁首

 留言（若有指正、疑問……可利用這裡留言）  
EpisteMath

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有
編輯：李渭天最後修改日期：9/18/2001
Posted by at

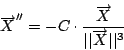
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)