用一些简单的arguement来估计复杂系统的行为。最常见的就是比较一些具有特征尺度的量。举些例子来说吧。
1 宏观低速下的问题，在做计算前，你就知道要用牛顿力学处理，这个决定就依赖于物理图像或物理直觉。(低速比较的是系统的速度与光速，宏观比较的是系统的大小和其德布罗意波长)。
2 Mermin Wangner theorem 具有连续对称性(compact Lie)，短程相互作用的低维系统在有限温度没有自发对称性破缺。用物理图像，就是long range fluctuation 几乎不消耗能量(连续对称性使得局部可做无穷小变动，短程相互作用使得此变动几乎不消耗能量。)于是系统没有long range order...
低维系统fluctuation重要。画个 n 维lattice，产生一个n-1维的domain wall. 然后发现创造domain wall所需要能量随n 增大而增大，而entropic gain几乎不变。于是高维fluctuation不重要。所以平均场理论高维好。就有了所谓的upper critical dimension.
3 自发对称性破缺产生gapless mode 这个非常图像: 想像一个势能面有一个低谷(基态)，然后该最低点凸起，形成一圈能量相同的极小值区域。于是新的mode就是在这一圈极小点上的运动，可以想象这就是U(1) phase fluctuation...超流系统最核心的量就是这个phase了。
4 restricted Hartree-Fock计算氢气分子解离时能量远远高估。其实就是个简单的图像，多体波函数是含有相同比重的离子与共价键的线性组合 ，当分子解离后，显然电子一边一个，两个去一边构成离子构型显然能量高。所以换成unrestricted Hartree-Fock就除去了共价成分，自然能描述好解离(不过会带来一个问题哦)。
5 time-dependent density functional theory 计算charge transfer excitation 会低估能量。图像: xc potential local, 不可能有1/r 的渐进行为，低估了产生跃迁偶极所需的能量。
6 凝聚态里常引入特征温度，方便引入物理图像。如Fermi temperature。对于金属而言远大于室温，也就是说温度效应影响不大。还有一些温度(能量尺度)也常用来做估计，如kondo temperature,只有温度低于特征温度才能看到，否则由温度产生的声子散射将主要贡献电阻。
7 Lieb-Robinson bound, exponential decay of correlation for gapped system等等也都是图像很清晰的，短程相互作用于是使得信息传播在有限时间不可能到很远。于是local operation不能有限时间传播很远。自然而然给出了correlation decay.而Lieb-Robinson velocity给出了decay 的scale...
8 weak localization 这个图像更清楚。disorder 系统中，电子被杂质散射，于是会走一个loop回到原点。常画的图是，电子顺时针走一圈，逆时针走一圈，回到同一个位置会interfere constructively,于是等效于电子在这点变得localize了，区别于anderson localization 这个前加了weak。 那么，这个loop要多大能？从图像其实非常清晰，必须小于phase decoherence length啊，否则没有coherence哪来的interference? 再问，如何除去？ 加磁场啊，有磁通穿过loop,那么就有机会把interfere constructively 变为 destructively。再问，如果有spin orbit coupling如何？antilocalization!(why?) 即使要从微观模型画Feynman图，从这个图像你都知道那类图最重要(cooperon)。
9 Andreev reflection也有个好图像。金属的电子要进入超导体，当偏压小于超导gap时进不去啊。于是在表面反射成空穴。等效于两个电子进入超导形成cooper pair...接着可以理解Andreev bound state， 超导|金属|超导 Junction。金属的电子在碰到界面便反射成空穴，碰到另一个界面又反射成电子，如此反复，形成驻波，便是Andreev bound state. 这个驻波需要电子和空穴的动量(在相位上)，与junction长度，两边相位差匹配(驻波条件)，画个图就能轻松决定这个态的能量了。
10 如何实现topological superconductor in 1d? 我老板做了很多工作，但都是从物理图像出发的: 需要p-wave, spinless fermion, 如何构造模型实现？ 用BCS s-wave superconductor,加spin-orbit coupling不就产生p-wave了么？加强磁场，把系统变成spin polarized, 不就是effectively spinless了么？有了图像，写模型做计算太容易了。
总之，物理图像对理论物理非常非常重要！我老板感觉太好，常常在我做计算前把答案都能猜得差不多
意识是一种物质形态
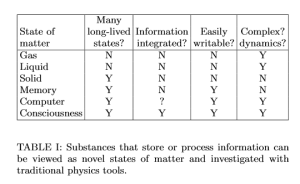
今天在arXiv上读到了一篇非常有趣的论文，由MIT的物理学家Max Tegmark撰写，名为《 Consciousnessas a State of Matter》(作为物质状态的意识）。他认为，自我意识可以认为是某种物质形态，如文中的表一所示，意识必须同时包含有长期存在的状态，集成化的信息，容易写入性，以及复杂的动力学。气体，液体，固体，乃至计算机都只能满足一部分判据。
为了解释意识可以被看成是物质的一种形态，他提出了六条原理，见表二
利用这些原理，他主要研究了”量子因子分解问题“，或者说作为一个有意识的的观察者，比如说我们，为什么可以感受特定的希尔伯特空间分解所对应的经典空 间，而不是傅里叶空间。或者更一般的，为什么我们把周围的世界理解为动态的层级，其中包含许多强烈集成且相对独立的物体。他认为，这个原理与所谓的从头开 始物理问题（physics-from-scratch）有关：我们如何才能从不过两个厄米矩阵中提取出三维空间和我们周围的半经典世界。能否仅从哈密顿 量H中提取出这些信息，而H完全可以仅从它的本征能谱来描述。
为了解释意识可以被看成是物质的一种形态，他提出了六条原理，见表二
接下来，Max Tegmark详细的讨论了什么叫做Integration(整体性)。在他看来，我们的世界是分层次的客体。比如说，你正在喝一杯冰水，你会感受到在玻 璃杯中有冰块。玻璃和冰块是分立的客体，因为它们都各自是一个整体且相对独立，它们内部的联系远远比与外部的联系紧密。我们可以定义物体的稳定性为集成温 度（把整体分离为部分所需的能量密度）和独立性温度（在层级内把母辈物体分离开所需的能量密度）之比。比如说，冰块的独立温度大概是3毫开，集成温度大概 是300开，稳定性是
。在下一级的结构中，氧原子和氢原子的稳定性都是10。氧原子核的稳定性是。稳定性越高，这个物体越容易被我们感知和定义。他发现，利用纠错码，经典物理允许信息基本上完全地被集成。任意一个包含至少半个比特的信息的子系统就可从剩下的比特中重建出来。存储在Hopeld neural networks (Hopeld神经网络）中的信息是天然的可纠错的。但是
个 神经元只能支持大概37个比特的集成了的信息。这就带来了一个集成化的悖论：为什么在我们意识体验所包含的信息内容似乎远大于37个比特。更糟的是，他发 现把这个结果推广到量子信息领域，反而加重了集成性悖论：量子信息系统只能支持不多于四分之一集成化的比特。实际上，对于任意大的量子系统，无论我们如何 编码，它所包含的可集成的信息都不会超过四分之一个比特。这强烈的暗示我们，集成性原理至少需要一个附加的原理作为补充。他接下来探讨了独立性原理，讨论了如何通过希尔伯特空间分解实现其对应的哈密顿量分立为互相独立的部分。他发现了量子芝诺效应悖论：如果我们把宇宙分为最 为相互独立的几个客体，那么所有的运动都会陷入中止。既然有意识的的观察者显然没有感受到任何的停滞，那么集成性和独立性原理必须还需要至少一个原理来作 为补充。
进一步的，他研究了动力学原理，因为有意识的系统不仅能存储信息，还要能处理它。他认为能量相干性（energy coherence）
可以作为动力学的合适度量，它与时间无关，且在某些纯态情况下约化为能量的不确定性
。把动力学最大化只会导致无聊的周期解，无法支撑复杂的信息处理。但是减小到合适的值时，将出现混沌和复杂的动力学，能遍历希尔伯特空间的所有维度。他 发现高度的自主性（独立性和动力学原理的结合）即使在一个高度开放的系统中也是可以实现的。由上可知，Max Tegmark并未解决量子分解问题，但是这些结果可以帮助人们聚焦问题，并能强调具体的公开子问题和从观察得来的各种暗示和线索 。他还提出了一些公开的问题：
- 因子分解和鸡与蛋的问题：量子态和分解哪个先哪个后？
- 因子分解和集成化悖论
- 因子分解和时间的浮现
No comments:
Post a Comment