誰來對我高談闊論「薛丁格方程式」 @ 想和妳看棒球:: 痞客邦 ...
bimeci.pixnet.net/blog/.../176769903-誰來對我高談闊論「薛丁格方程...
誰來對我高談闊論「薛丁格方程式」
西元1926年,奧地利物理學家薛丁格(Erwin Schrödinger)發表薛丁格方程式(Schrödinger Equation),奠定了「量子力學」發展的基礎。

【Erwin Schrödinger】
這個最基本的量子力學方程式描述了一個量子系統如何隨時間演變的關係:

其中Ψ為物質波函數,m為粒子質量,V為位能,h為普朗克常數且
 ,而
,而 則為三維空間中的拉普拉斯算符。關於薛丁格方程式的涵義,簡單來說,在量子的微觀尺度下,粒子有時會顯示出波動性質,有時又會顯示出粒子性質,這樣的特徵稱為「波動-粒子二象性(wave-particle duality)」,而薛丁格方程式則描述了微觀粒子的波動行為,也揭示了「物質波」的存在。
則為三維空間中的拉普拉斯算符。關於薛丁格方程式的涵義,簡單來說,在量子的微觀尺度下,粒子有時會顯示出波動性質,有時又會顯示出粒子性質,這樣的特徵稱為「波動-粒子二象性(wave-particle duality)」,而薛丁格方程式則描述了微觀粒子的波動行為,也揭示了「物質波」的存在。Question:既然「波動-粒子二象性」揭示了物質波的存在,但薛丁格波動方程式中為什麼會有虛數i呢?很難想像,為什麼確實存在的物質會牽扯到虛無飄渺的複數,它的物理意義到底是什麼?
我們若要描述一個波動行為,必須說明波動系統隨時間變化時的能量狀態,是一種隨著時間演變而傳遞能量的表現。所以,探討波動能量與時間變化的關係,即為波動方程式:

其中
 為時間t的算符,表示波函數對時間的某種變化形式。
為時間t的算符,表示波函數對時間的某種變化形式。 為哈密頓算符,它應對到波動系統的總能量E。對於像水波、聲波或光波等一般我們所熟悉的波動,它們的波動方程式基本表達形式皆為波函數對時間的二次微分方程式:
為哈密頓算符,它應對到波動系統的總能量E。對於像水波、聲波或光波等一般我們所熟悉的波動,它們的波動方程式基本表達形式皆為波函數對時間的二次微分方程式:
然而,薛丁格方程式卻是:

不僅物質波函數對時間的變化形式為一次微分,而且更出現虛數i!當初薛丁格寫出方程式時也是霧煞煞,甚至嘗試要消除虛數i,結果最後發現這是行不通的。物質波本身就是含有虛數的「複函數」,並滿足複時變方程。物質波的複數性質到底代表什麼?或許,您可以先從物質波函數的特性與薛丁格方程式的形式出發,來探討存在虛數i的物理意義。
觀察薛丁格方程式的數學解,我們可以發現最好要有一個函數,在一次微分後與自己成正比。另外,這個函數必須能隨時間變化而具有週期震盪的性質,才能符合波動行為的數學形式,而「虛數」的指數函數正好是這樣的函數:

一次微分後與自己成正比:

又有週期震盪性質的三角函數形式:

此即為存在虛數i的原因之一,但這只是數學上的結果論,因為方程式中有虛數i,所以物質波函數的解當然也要以複數形式表現。若物質波函數是完全實數的話,那麼薛丁格方程式是否就不會出現虛數了?這是一個很好的懷疑,然而,若繼續追究物質波的能量本質,您將會發現一個不同於一般認知的世界,也就是量子世界的特徵「波動-粒子二象性」,以及它與虛數i的奇妙關係。
约化普朗克常量(又称合理化普朗克常量)是角动量的最小衡量单位
普朗克常数记为 h ,是一个物理常数,用以描述量子大小。在量子力学中占有重要的角色,马克斯·普朗克在1900年研究物体热辐射的规律时发现,只有假定电磁波的发射和吸收不是连续的,而是一份一份地进行的,计算的结果才能和试验结果是相符。这样的一份能量叫做能量子,每一份能量子等于hv,v为辐射电磁波的频率,h为一常量,叫为普朗克常数。普朗克常数的值约为:6.626196×10^-34 J·s
其中为能量单位为焦(J)。
普朗克常数的物理单位为能量乘上时间,也可视为动量乘上位移量:
(牛顿(N)·米(m)·秒(s))为角动量单位
由于计算角动量时要常用到h/2π这个数,为避免反复写 2π 这个数,因此引用另一个常用的量为约化普朗克常数(reduced Planck constant),有时称为狄拉克常数(Dirac constant),纪念保罗·狄拉克:
h(这个h上有一条斜杠)=h/2π
约化普朗克常量(又称合理化普朗克常量)是角动量的最小衡量单位。
其中 π 为圆周率常数 pi。 念为 "h-bar" 。
普朗克常数用以描述量子化,微观下的粒子,例如电子及光子,在一确定的物理性质下具有一连续范围内的可能数值。例如,一束具有固定频率 ν 的光,其能量 E 可为:
有时使用角频率 ω=2πν :
许多物理量可以量子化。譬如角动量量子化。 J 为一个具有旋转不变量的系统全部的角动量, Jz 为沿某特定方向上所测得的角动量。其值:
因此, 可称为 "角动量量子"。
普朗克常数也使用于海森堡不确定原理。在位移测量上的不确定量(标准差) Δx ,和同方向在动量测量上的不确定量 Δp,有如下关系:
西元1924年,也就是薛丁格方程式誕生前兩年,法國物理學家德布羅意(Louis de Broglie)提出了「物質波」的假設。當時普朗克的黑體輻射實驗與愛因斯坦對光電效應的研究,已揭示出光子能量、動量與頻率、波長之間的關係:


但德布羅意認為不僅只有光子,所有粒子的頻率與波長都可以從能量與動量求得,每一種微觀粒子都具有波動性與粒子性的「波動-粒子二象性」。德布羅意的劃時代論文開啟了量子力學的新紀元。

【Louis de Broglie】
現在,我們可嘗試允許物質波函數的波動方程式為虛數的指數函數形式:

代入薛丁格方程式:

注意!奇妙結果出現了:

我們可以發現,薛丁格方程式正好符合波動隨著時間演變而傳遞能量的表現形式。至此,物質波函數對時間的變化形式為一次微分,已非胡亂猜測,而是符合波動物理學的基本性質,若拿掉虛數,薛丁格方程式反而不可能導出符合
 的能量特徵值。「波動-粒子二象性」的特徵本質賦予了「虛數i」必要存在的意義,物理學的可測量終於拓展到了複數。
的能量特徵值。「波動-粒子二象性」的特徵本質賦予了「虛數i」必要存在的意義,物理學的可測量終於拓展到了複數。繼續探討薛丁格方程式與能量的關係。動能與位能的合為總能量,而動量與動能則有以下關係式:

總能量:

考慮「波動-粒子二象性」,
 代入總能量得:
代入總能量得:
薛丁格方程式成為:

最後代入拉普拉斯算符
 ,此即為對應特徵總能量的薛丁格方程式:
,此即為對應特徵總能量的薛丁格方程式:
其中:

薛丁格方程式不直接寫出頻率與波長,適用於任何單頻率波以及它們的線性「疊加」,因此也就適用於任何物質波。薛丁格方程式最重要的特徵在於虛數i,所以物質波函數的解也必須一定是複數形式。複數形式的波函數,它的本質是什麼呢?西元1926年,薛丁格方程式誕生同年,德國猶太裔物理學家玻恩(Max Born)立即發表論文指出,薛丁格的波函數是一種機率振幅(probability amplitude),其絕對值平方對應測量到粒子的機率分佈。物質波就是機率波,薛丁格方程式的物理涵義才逐漸明朗。
【Max Born】
薛丁格方程式所描述的波動力學,簡單來說就是揭示了粒子在時空中的行為竟然和機率有關!這種隨機性,使一向要求準確的物理學充滿不確定感,總覺得讓人難以接受,也難怪愛因斯坦要持反對看法:「我不能相信上帝是在擲骰子!」

【Solvay Conference 1927】
西元1927年,幾乎所有量子力學方面的權威人士,都一起出席了在比利時首都布魯塞爾舉行的第五屆索爾維會議(Solvay Conference),可視為向全世界正式宣示創立量子力學。會議中,科學家們對機率波一直爭論不休,而薛丁格尤其不高興。對薛丁格來說,他的波是真實的波,怎麼可以解釋為機率呢?不論日後正反兩派對「機率波」的辯論大戰如何進行,「量子力學」再次顛覆了傳統物理學的思想,並逐步證明機率本質理論的正確性,成為近代物理學發展的兩大支柱之一。
一個『擾動』可以數學上描述為
這就將我們帶進了所謂的『一維波動方程式』。
http://www.freesandal.org/?paged=4&m=201409
按月彙整:2014 年 09 月
【Sonic π】聲波之傳播原理︰原理篇《三》
我們已經知道,在物理上『波』是『空間』或者『物質』中『擾動』的『傳播現象』。它在傳播時『波前』將『能量』由此處帶往彼處,通常『波』即使需要透過『介質』傳播,構成那個介質的『物質粒子』在『波前通過時』並不會產生『永久性位移』之變化,也不會一併跟著『波前前進』發生了『物質傳送』的現象。假使說將『波前』想像成空間『擾動式樣』,分布在『介質』的『空間』裡,那麼『波前』在『時間』中行徑之『變化』,也就是『波傳播』的『時空圖像』了。自然界各種不同類型的『波』,不論它是『機械的』還是『非機械的』都可以由廣義的『波動方程式』來描述,然而『具體現象』之『□□波』的『數學形式』,卻是各有各的不同。
一個『振動』的『音叉』因為與『周遭空氣』的碰撞傳遞『能量』給空氣中的某些『分子』,然後這些分子又去碰撞『周遭另一些分子』將『振動』漸次依時傳遞下去。然而在『傳遞振動』時,先時碰撞之『所得』將為此時碰撞之『所失』,因此『空氣分子』並不會因為『傳播聲音』就跟著聲音『一塊跑了』!!
一個『振動』的『音叉』因為與『周遭空氣』的碰撞傳遞『能量』給空氣中的某些『分子』,然後這些分子又去碰撞『周遭另一些分子』將『振動』漸次依時傳遞下去。然而在『傳遞振動』時,先時碰撞之『所得』將為此時碰撞之『所失』,因此『空氣分子』並不會因為『傳播聲音』就跟著聲音『一塊跑了』!!
如果說一個『擾動』可以數學上描述為
這就將我們帶進了所謂的『一維波動方程式』。由此來推測這個『偏微分方程式』的『通用解』將可以表示為:
在 x 軸上一個向左傳播的波和一個向右傳播的波的疊加。
在數學的描述上,一維波動方程式定義為︰
前面所講的『波前保形』傳播想法,舉例來說它可以是一個『平面波』在『均勻介質』中的傳播,或者說是某種『自然』或『人為』的『線型水面波』 。大自然中的『現象』有時會『指引』數學上『求解』的『方向』,因為終究人們能夠發現的那個現象方程式,也是來自於『大自然』的啊!!難到一個不受外物影響的『波前』它在  時刻的『相同相位』──
時刻的『相同相位』──  ── 之點,到了
── 之點,到了  時刻就會變成不一樣的嗎??
時刻就會變成不一樣的嗎??
,這樣那個方程式就變成了
,此處的
『求解』再變換回
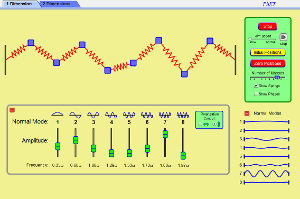
為了闡明『波』的傳播與簡諧振子『振動』的密切關係,就讓我們考慮一個由『彈簧與質點』所構成的『彈簧鏈模型』物理系統︰
有

圖中
假使這個彈簧鏈物理系統不受其它外力作用,如果我們分析作用在位於
此處
它可以用整個物理系統的常量
如果設想一條長度
比之於一維波動方程式,於是得到波速
果真是此處
【Sonic π】聲波之傳播原理︰原理篇《二》
惠更斯原理
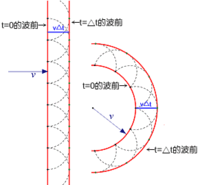
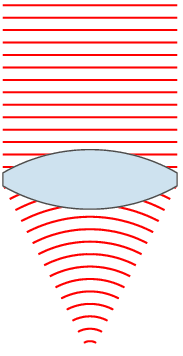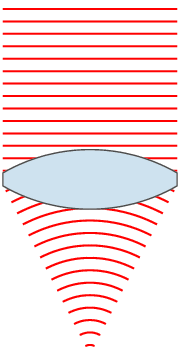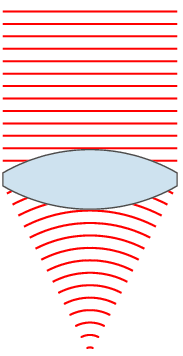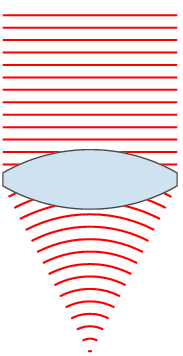
在『波前』wavefront 上的每一個點都可以將它看成是產生『球面次波』Spherical secondary waves 的『點波源』,而在這『之後』任何時刻的『波前』則可看作是這一些『相同相位子波』的『包絡』Envlope 『線』或者『面』。
那麼什麼是『包絡』的呢?從幾何學上講,一個『曲線族』的『包絡線』與該曲線族中的每一條曲線都『相切』tangent to 於某一點。一七三四年法國數學家亞歷克西斯‧克勞德‧克萊羅 Alexis Claude de Clairault 提出 方程式。如果將該方程式對變數
方程式。如果將該方程式對變數  再次作『微分』得到
再次作『微分』得到  ,因此
,因此  或者
或者  。假使
。假使  ,那麼
,那麼  是一個『常數』,將之代入原方程式得到『曲線族』
是一個『常數』,將之代入原方程式得到『曲線族』  的一般解。如果
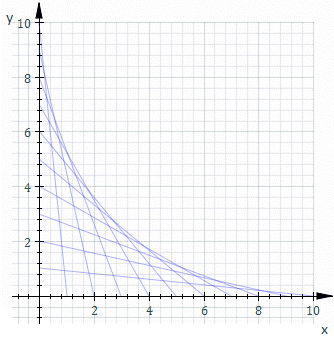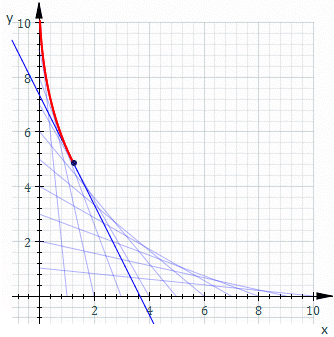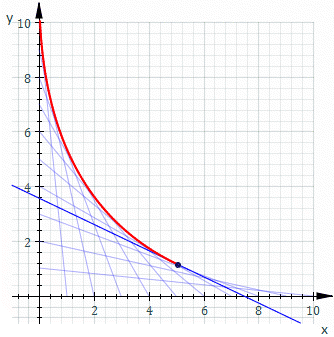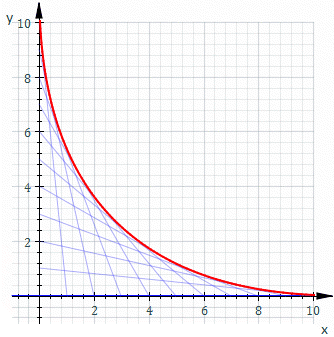
的一般解。如果  ,它的解是上述曲線族的『包絡線』。舉例而言,下圖是
,它的解是上述曲線族的『包絡線』。舉例而言,下圖是  的圖示
的圖示

其次『波前』的形狀可以被經過的『光學系統』所改變;而『相位相同』是講在 時間的波前『次波』都經過了『相同』的『時距』
時間的波前『次波』都經過了『相同』的『時距』 ,形成了
,形成了  新的波前。
新的波前。
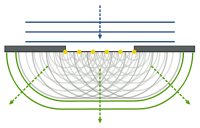
藉著這原理,惠更斯給出了波的『直線傳播』與『球面傳播』的『定性』解釋,並且推導出了『反射定律』與『折射定律』。但是他卻不能解釋,為什麼當光波遇到『銳邊』、『小孔』或『狹縫』時,會偏離了直線傳播,也就是說會發生『繞射』現象。除此之外『惠更斯原理』假設了『次波』只會朝著『行進方向』傳播;然而他並沒有解釋為什麼它們不可以朝反方向傳播的呢?
法國物理學家奧古斯丁‧菲涅耳 Augustin Fresnel ,是『波動光學理論』的主要創建者之一,在惠更斯原理的基礎上假設這些『次波會彼此發生干涉』 ,這就是現今所稱的『惠更斯‧菲涅耳原理』,是『惠更斯原理』與『干涉原理』的開花結果。一八一八年菲涅耳將他的論文提交給法蘭西學術院的評委會。評委會的會員西莫恩‧德尼‧帕松 Siméon Denis Poisson 認為假使菲涅耳的理論成立,那麼將光波照射於一小塊圓形擋板時,所形成的陰影之中央必定會有一個亮斑,因此他推斷這理論不正確。同時與會的弗朗索瓦‧讓‧多米尼克‧阿拉戈 François Jean Dominique Arago 親自動手做了這個實驗,結果與預測相符,證實了菲涅耳原理的正確無誤。這實驗是支持光波動說的強有力的證據,與楊氏的雙縫實驗共同反駁了牛頓主導的光粒子說。
在『波前』wavefront 上的每一個點都可以將它看成是產生『球面次波』Spherical secondary waves 的『點波源』,而在這『之後』任何時刻的『波前』則可看作是這一些『相同相位子波』的『包絡』Envlope 『線』或者『面』。
那麼什麼是『包絡』的呢?從幾何學上講,一個『曲線族』的『包絡線』與該曲線族中的每一條曲線都『相切』tangent to 於某一點。一七三四年法國數學家亞歷克西斯‧克勞德‧克萊羅 Alexis Claude de Clairault 提出

其次『波前』的形狀可以被經過的『光學系統』所改變;而『相位相同』是講在
藉著這原理,惠更斯給出了波的『直線傳播』與『球面傳播』的『定性』解釋,並且推導出了『反射定律』與『折射定律』。但是他卻不能解釋,為什麼當光波遇到『銳邊』、『小孔』或『狹縫』時,會偏離了直線傳播,也就是說會發生『繞射』現象。除此之外『惠更斯原理』假設了『次波』只會朝著『行進方向』傳播;然而他並沒有解釋為什麼它們不可以朝反方向傳播的呢?
法國物理學家奧古斯丁‧菲涅耳 Augustin Fresnel ,是『波動光學理論』的主要創建者之一,在惠更斯原理的基礎上假設這些『次波會彼此發生干涉』 ,這就是現今所稱的『惠更斯‧菲涅耳原理』,是『惠更斯原理』與『干涉原理』的開花結果。一八一八年菲涅耳將他的論文提交給法蘭西學術院的評委會。評委會的會員西莫恩‧德尼‧帕松 Siméon Denis Poisson 認為假使菲涅耳的理論成立,那麼將光波照射於一小塊圓形擋板時,所形成的陰影之中央必定會有一個亮斑,因此他推斷這理論不正確。同時與會的弗朗索瓦‧讓‧多米尼克‧阿拉戈 François Jean Dominique Arago 親自動手做了這個實驗,結果與預測相符,證實了菲涅耳原理的正確無誤。這實驗是支持光波動說的強有力的證據,與楊氏的雙縫實驗共同反駁了牛頓主導的光粒子說。
於此我們將簡單介紹一下菲涅耳的『實驗精神』,說一說『菲涅耳原理』的『數學表達』

如上圖所示,假使『點波源』
根據惠根斯原理以及波的疊加原理,將所有與點
常數因子意謂著『次波』與『主波』的相位差為
式中,
因此,在點
此處,
當然從『克希荷夫繞射公式』,可以推導出惠更斯‧菲涅耳原理。而且並不需要菲涅耳提出的『假設』與『修正』,它們會在推導的過程中,自然而然的顯露出來。因此惠更斯‧菲涅耳的表達式可以看成是克希荷夫繞射公式的一種近似。同時克希荷夫給出了『傾斜因子 』
於是可以知道,當
讓我們玩一玩『電子繞射』的現象吧︰
假使你的電腦上沒有『Java Web Start』,然而安裝了『java』,請至 PhET 的這個網頁直接下載『davisson-germer_en.jar』的檔案。然後用『java -jar 檔名.jar』執行。
【Sonic π】聲波之傳播原理︰原理篇《一》
光的『本性』到底是什麼?一個光的『折射問題』就曾經在科學史上引發過大『論戰』!追根溯源西元二世紀時古希臘的托勒密 Claudius Ptolemy 在所著之《光學》Optics 第五卷裡,提出了他的折射實驗與定律。也許在那個時代,並不清楚『正弦』Sin 的概念,所以他結論並不正確。其後於九八四年伊朗學者伊本‧沙爾 Ibn Sahl 在《論點火鏡子與透鏡》On Burning Mirrors and Lenses 裡最早正確地描述了『折射定律』,並且將之應用於找出能夠讓『光聚焦』而又不會產生『幾何像差』之『透鏡』的形狀。然而只可惜他的研究結果並未為其它的學者所注意到。因此往後的許多年,人們又再次的從托勒密的『錯誤理論』開始『研究折射』。到了十一世紀初阿拉伯的學者海什木 Al Hazen 『重新再做』托勒密的實驗,雖然在著作的《光學書》Book of Optics 中總結出了一些法則,卻也沒能夠得出折射的『正弦定律』。如此又過了五百年,一六零二年英國天文學家托馬斯‧哈里奧特 Thomas Harriot 重新發現了『折射定律』,不過他並沒有發表這個結果,只是在與德國天文學家約翰內斯‧克卜勒 Johannes Kepler 通信中曾提及過這件事。其後於一六二一年荷蘭天文學家威理博‧司乃耳 Willebrord Snellius 推導出了一個數學上的『等同形式』,然而在其有生之年,人們並不知道他的成就。作者雖然不知這些偉大的『天文學家們』為何當時『人不知』他們的『研究結論』?然而設想從事『竹藤工藝』者,假使不知道『如何彎曲』那個『竹片』與『藤條』的話,大概想做『什麼家具』都可能是困難的吧!那麼如果不知道如何『屈折光線』,一個天文學家又怎麽能夠製造『好的透鏡』,用以『觀測天象』的呢??
一六三七年法國的大哲學家勒內‧笛卡兒 René Descartes 在其專著《屈光學》Dioptrics 裡,推導出了這個『折射定律』,並且用自己的理論解析了一系列的『光學問題』。在這推導裡,他做了兩個『假設』︰一、『光』的『傳播速度』與周遭的『介質密度』成『正比』;二、『光的速度』沿著『交界面』方向的『速度分量守恆』。一六六二年法國律師和業餘數學家皮埃爾‧德‧費馬 Pierre de Fermat 發表了『最短時間原理』:光線傳播的路徑是需時最少的路徑。藉此推導出了『折射定律』,但是該原理假設了與笛卡兒相反之『光的傳播速度與介質密度成反比』,為此費馬強烈的反駁笛卡兒的導引,認為笛卡爾的假設是錯誤的。根據歷史學者以撒‧福雪斯 Issac Vossius 一六六二年在著作《De natura lucis et proprietate》裏的敘述,笛卡兒事先閱讀了司乃耳的論文,然後調製出自己的導引。有些歷史學者覺得這指控太過誇張,令人難以置信;也有很多歷史學者都存疑過曾經發生了這回事,然而費馬與惠更斯卻分別多次重複地譴責笛卡兒之行為缺失。在此不論歷史上的『是非對錯』,這場光的『粒子說』與『波動說』之大戰正方興未艾!一六六四年英國博物學家羅伯特‧虎克 Robert Hooke 開始提倡光的『波動說』。但是一六六九年被授予劍橋大學三一學院盧卡斯數學教授席位的牛頓卻是笛卡兒的『光粒子說』之發揚者。一六七零年到一六七二年期間,牛頓負責在校講授光學。他研究了光的折射,發表『三稜鏡』可以將白光發散成彩色光譜,而且藉著透鏡和另一個三稜鏡可以將彩色光譜合組為白光。雖然虎克本人曾經公開批評牛頓的光微粒說。但是因為牛頓在多門物理領域的成就,使得他被公認是這場『光本性爭論』的贏家。
一六七八年荷蘭物理、天文和數學家克里斯蒂安‧惠更斯 Christiaan Huygens 依據虎克的提議,在其著作《光論》(Traité de la Lumiere)裡應用他創造的『子波原理』 ── 今天的惠更斯原理──,從光的波動性質,成功的推導出並且解釋了司乃耳定律。之後於一七零三年惠更斯在其著作《Dioptrica》中又談到了這定律,並且正式的將這定律的發現歸功於司乃耳。一八零二年英國的科學家與醫生托馬斯‧楊 Thomas Young ── 被譽為『世界上最後一個什麼都知道的人』 ── 做實驗發現,當光波從較低密度介質傳播到較高密度介質時,光波的波長會變短,他因此歸結出光波的傳播速度會降低。楊氏之所以大名鼎鼎在於他所提出的『雙縫實驗』 double-slit experiment 就是這一場『古典光本性大戰』勝負之最終『判定性實驗』。之後這個『光本性問題』又發生了量子力學史上的『愛因斯坦‧波耳』大戰,以及波耳所提出的『波、粒互補性原理』。那麼光到底是什麼呢??請看
這段動畫影片道盡了現今科學所了解的『量子本性』,妙哉!沒有『觀察者』時它是『波』,想確定『它』而『作觀察』時,它又是『粒子』,果真是 Oh! My God !!
也就是說『費馬原理』可以讓你『改造』樹莓派『攝像模組』的『眼睛』,讓它能夠『看的更遠』或者『顯現微物』,如此各類『攝影』將會更『得手應心』的了!!
光的『反射定律』推導

假設光線從 點出發經過
點出發經過  點,被反射到
點,被反射到  點。那麼這個『光徑函數』
點。那麼這個『光徑函數』
 是
是
 。
。
根據費馬原理,光線會選擇光徑函數為極值的路徑。因此 ,所以得到
,所以得到
 。
。
然而

 。
。
故得 ,
,
這就是光的『反射定律』。
光的『折射定律』推導

假設光線從左方『折射率』為 的介質一的
的介質一的  點,經過
點,經過  點到達『折射率』為
點到達『折射率』為  的介質二之
的介質二之  點。由『光速』的『費馬假設』我們可以得到這兩個介質中的光速為
點。由『光速』的『費馬假設』我們可以得到這兩個介質中的光速為


,式中 是『真空光速』。那麼這條光線沿著
是『真空光速』。那麼這條光線沿著  走,所需要的時間『光時函數』
走,所需要的時間『光時函數』
 是
是
 。
。
根據費馬原理,光線會選擇所需時間為最短的路徑,於是 ,所以得到
,所以得到
 。
。
然而


故得 。
。
這就是司乃耳『折射定律』。
一六三七年法國的大哲學家勒內‧笛卡兒 René Descartes 在其專著《屈光學》Dioptrics 裡,推導出了這個『折射定律』,並且用自己的理論解析了一系列的『光學問題』。在這推導裡,他做了兩個『假設』︰一、『光』的『傳播速度』與周遭的『介質密度』成『正比』;二、『光的速度』沿著『交界面』方向的『速度分量守恆』。一六六二年法國律師和業餘數學家皮埃爾‧德‧費馬 Pierre de Fermat 發表了『最短時間原理』:光線傳播的路徑是需時最少的路徑。藉此推導出了『折射定律』,但是該原理假設了與笛卡兒相反之『光的傳播速度與介質密度成反比』,為此費馬強烈的反駁笛卡兒的導引,認為笛卡爾的假設是錯誤的。根據歷史學者以撒‧福雪斯 Issac Vossius 一六六二年在著作《De natura lucis et proprietate》裏的敘述,笛卡兒事先閱讀了司乃耳的論文,然後調製出自己的導引。有些歷史學者覺得這指控太過誇張,令人難以置信;也有很多歷史學者都存疑過曾經發生了這回事,然而費馬與惠更斯卻分別多次重複地譴責笛卡兒之行為缺失。在此不論歷史上的『是非對錯』,這場光的『粒子說』與『波動說』之大戰正方興未艾!一六六四年英國博物學家羅伯特‧虎克 Robert Hooke 開始提倡光的『波動說』。但是一六六九年被授予劍橋大學三一學院盧卡斯數學教授席位的牛頓卻是笛卡兒的『光粒子說』之發揚者。一六七零年到一六七二年期間,牛頓負責在校講授光學。他研究了光的折射,發表『三稜鏡』可以將白光發散成彩色光譜,而且藉著透鏡和另一個三稜鏡可以將彩色光譜合組為白光。雖然虎克本人曾經公開批評牛頓的光微粒說。但是因為牛頓在多門物理領域的成就,使得他被公認是這場『光本性爭論』的贏家。
一六七八年荷蘭物理、天文和數學家克里斯蒂安‧惠更斯 Christiaan Huygens 依據虎克的提議,在其著作《光論》(Traité de la Lumiere)裡應用他創造的『子波原理』 ── 今天的惠更斯原理──,從光的波動性質,成功的推導出並且解釋了司乃耳定律。之後於一七零三年惠更斯在其著作《Dioptrica》中又談到了這定律,並且正式的將這定律的發現歸功於司乃耳。一八零二年英國的科學家與醫生托馬斯‧楊 Thomas Young ── 被譽為『世界上最後一個什麼都知道的人』 ── 做實驗發現,當光波從較低密度介質傳播到較高密度介質時,光波的波長會變短,他因此歸結出光波的傳播速度會降低。楊氏之所以大名鼎鼎在於他所提出的『雙縫實驗』 double-slit experiment 就是這一場『古典光本性大戰』勝負之最終『判定性實驗』。之後這個『光本性問題』又發生了量子力學史上的『愛因斯坦‧波耳』大戰,以及波耳所提出的『波、粒互補性原理』。那麼光到底是什麼呢??請看
這段動畫影片道盡了現今科學所了解的『量子本性』,妙哉!沒有『觀察者』時它是『波』,想確定『它』而『作觀察』時,它又是『粒子』,果真是 Oh! My God !!
在說費馬原理之前,讓我們先談談一個函數  如何求『極值』── 極大值、極小值或拐點 ── 的問題。假使我們把函數看成是『山巒起伏』,那麼從經驗上講『山頂』就是它比『週邊都高』的地方;而『山谷』就是它比『週邊都低』的位置,一般都會比較『平坦』。因此觀察一個函數之各個點的『斜率』就可以知道它的『起伏變化』,那一些『斜率為零』的『點』,就可能是該函數那個『點附近區域』裡的『最大值』或者『最小值』,當然也可能是『凹凸改變處』,這時叫做『拐點』或者『反曲點』,它並不是那個區域裡的『極大極小值』。在數學裡一個函數『求斜率』的方法就是將該函數『微分』
如何求『極值』── 極大值、極小值或拐點 ── 的問題。假使我們把函數看成是『山巒起伏』,那麼從經驗上講『山頂』就是它比『週邊都高』的地方;而『山谷』就是它比『週邊都低』的位置,一般都會比較『平坦』。因此觀察一個函數之各個點的『斜率』就可以知道它的『起伏變化』,那一些『斜率為零』的『點』,就可能是該函數那個『點附近區域』裡的『最大值』或者『最小值』,當然也可能是『凹凸改變處』,這時叫做『拐點』或者『反曲點』,它並不是那個區域裡的『極大極小值』。在數學裡一個函數『求斜率』的方法就是將該函數『微分』  。
。
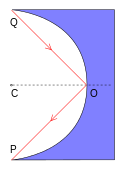
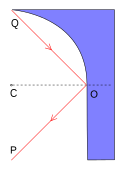
就像有人說的︰『費馬原理』也許不應該稱作『最短時間原理』,而是應該叫做『平穩時間原理』。因為事實上光線並非都是選擇這一條『時間最短』的路徑。比方說右圖的『半圓形鏡面』,光走得路徑  是反射路徑中的『最大值』。而在 『
是反射路徑中的『最大值』。而在 『 圓平面切合鏡面』圖中,光走得路徑
圓平面切合鏡面』圖中,光走得路徑  卻是那一個所有『可能路徑』函數中的『拐點』。而這個『平穩』是說著所有可能路徑
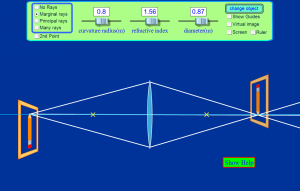
卻是那一個所有『可能路徑』函數中的『拐點』。而這個『平穩』是說著所有可能路徑  的『光徑函數』是『可微分的』這一件事。那麼這個『費馬原理』有什麼重要性嗎?它是『幾何光學』的基本原理,可以用來『推導』各類由『鏡面』與『透鏡』組合而成的『光學系統』的『成像原理』。『理解』種種『光學設備』── 望遠鏡、顯微鏡、放大鏡、近視眼鏡… ── 的『設計原理』。
的『光徑函數』是『可微分的』這一件事。那麼這個『費馬原理』有什麼重要性嗎?它是『幾何光學』的基本原理,可以用來『推導』各類由『鏡面』與『透鏡』組合而成的『光學系統』的『成像原理』。『理解』種種『光學設備』── 望遠鏡、顯微鏡、放大鏡、近視眼鏡… ── 的『設計原理』。
光的『反射定律』推導

假設光線從
根據費馬原理,光線會選擇光徑函數為極值的路徑。因此
然而
故得
這就是光的『反射定律』。
光的『折射定律』推導

假設光線從左方『折射率』為
,式中
根據費馬原理,光線會選擇所需時間為最短的路徑,於是
然而
故得
這就是司乃耳『折射定律』。
【Sonic π】聲波之傳播原理︰振動篇
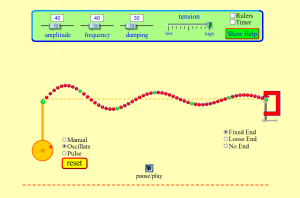
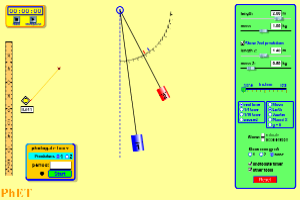
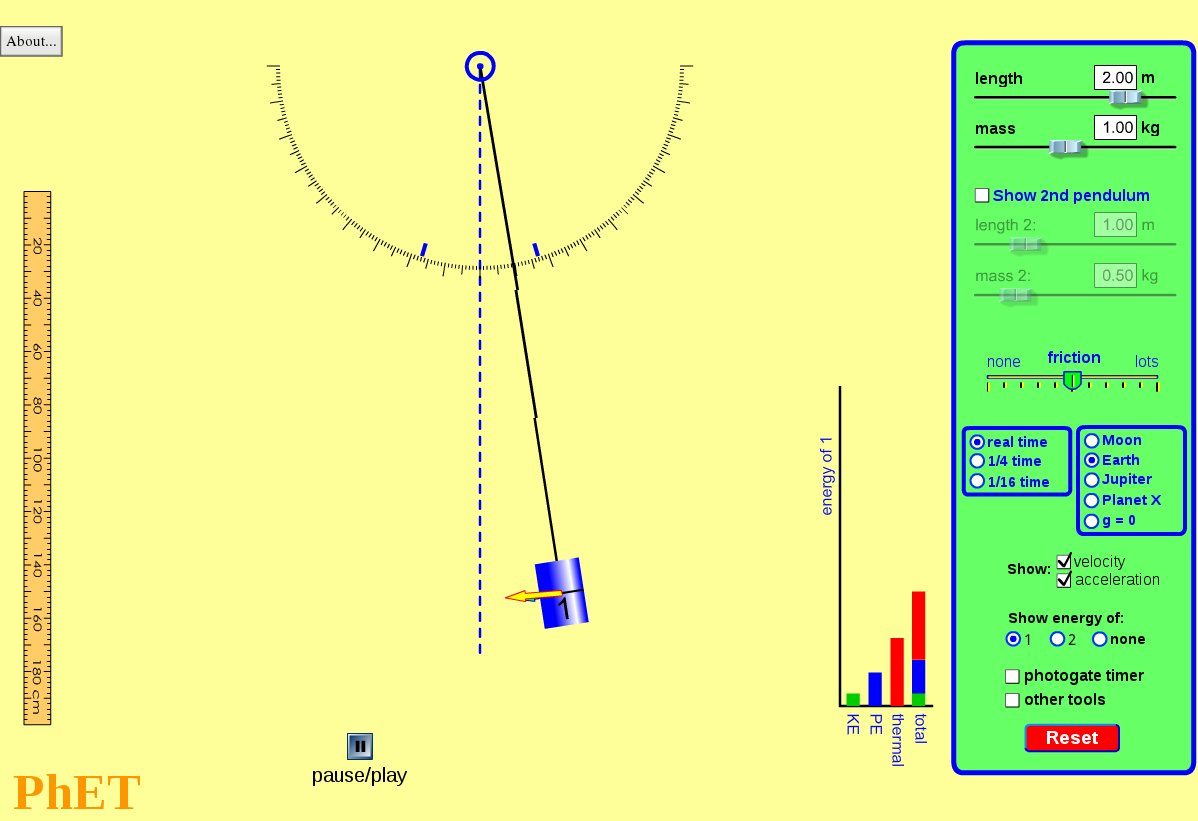
來自於美國科羅拉多大學的 PhET Physics Education Technology 計劃,免費提供以樂趣、互動與研究為基礎的物理現象模擬軟體。這一個計畫是由二零零二年美國諾貝爾物理學獎得主之一的卡爾‧埃德溫‧威曼 Carl Edwin Wieman 所發起,根據 WiKi 上所載
began with Wieman’s vision to improve the way science is taught and learned. Their stated mission is “To advance science and math literacy and education worldwide through free interactive simulations.”
,按照現今官網的說明
About PhET
PhET provides fun, interactive, research-based simulations of physical phenomena for free. We believe that our research-based approach- incorporating findings from prior research and our own testing- enables students to make connections between real-life phenomena and the underlying science, deepening their understanding and appreciation of the physical world.
…
目前它的線上內容早已經括及多類科學領域,並且很多內容也有了中文的翻譯網頁。作者認為如何用計算機輔助『教育』與『學習』正是今日當有之重要的『學習工具』,實現人們可以用『科學』來解釋『日常生活』中所經驗到的種種『自然現象』的教育宗旨。當你閱讀本文看到有『點擊啟動』的圖片時,請在『點擊啟動』的方形區域外,使用『滑鼠左鍵』點擊圖片的任何位置,進入嵌入式『PhET』線上模擬器的軟體世界。
依據牛頓第二運動定律,一個簡諧振子的方程式為
 ,它的解是
,它的解是
 ,此處
,此處  是『相位角』,
是『相位角』,
 ,式中
,式中  是『角頻率』,
是『角頻率』, 是『周期』。
是『周期』。
也就是說簡諧振子是一種『頻率』為 ,『振幅』為
,『振幅』為  的週期運動。假設
的週期運動。假設  的初始時,
的初始時, ,得到
,得到


動能 = ,位能=
,位能= ,系統總能量
,系統總能量

由此可以知道簡諧振子的系統總能量是一個常數,這稱之為『能量守恆量』定律,它和『振幅』的平方成正比。它的『頻率』 只依賴於系統『固有』的
只依賴於系統『固有』的  與
與  ,也是一個不變的常量。
,也是一個不變的常量。
依據牛頓第二運動定律,一個受驅振子的方程式為
 ,一般將之改寫為
,一般將之改寫為
 ,此處
,此處  稱為『無阻尼』角頻率,而
稱為『無阻尼』角頻率,而  叫做『阻尼比率』。如果『外力』
叫做『阻尼比率』。如果『外力』 ,那個方程式就成了『阻尼振子』的方程式
,那個方程式就成了『阻尼振子』的方程式
 ,當
,當  它的解是
它的解是
 ,此處
,此處  是相位角。
是相位角。
假使 它的解是
它的解是
 。
。
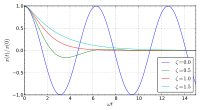
如果我們從 的值來看『阻尼振子』的系統行為,當
的值來看『阻尼振子』的系統行為,當  時,這一個系統已經『振動』不起來了,通常叫做『過阻尼』,負數的『指數項』使得系統的能量隨時間逐漸減少,
時,這一個系統已經『振動』不起來了,通常叫做『過阻尼』,負數的『指數項』使得系統的能量隨時間逐漸減少, 的數值愈大能量減少將慢愈遲回到平衡。當
的數值愈大能量減少將慢愈遲回到平衡。當  時,這一個系統也『振動』不起來了,通常稱之為『臨界阻尼』,此時系統會用最快的方式設法回到平衡,這個可是『關門』系統的『最佳解』!!。當
時,這一個系統也『振動』不起來了,通常稱之為『臨界阻尼』,此時系統會用最快的方式設法回到平衡,這個可是『關門』系統的『最佳解』!!。當  時,這樣的諧振子系統稱作『低阻尼』,這時系統用著『低於無阻尼』的『頻率』振動,系統的『振幅』隨著時間以
時,這樣的諧振子系統稱作『低阻尼』,這時系統用著『低於無阻尼』的『頻率』振動,系統的『振幅』隨著時間以  為比率逐漸減小以至於『不振動』為止。事實上從自然界中來的一般現象都會比『理論值』更快的到達『停止點』,就像說不只有『動摩擦力』與『靜摩擦力』之區分,摩擦力的『速度相關性』也不是這麼『簡單的正比』之假設,更別說理論上還有著『摩擦生熱』的問題必須要考慮。我們也許可以說為著追求『基本現象的理解』,通常都會『假設』了一些數學上『解答問題』的『理想條件』。
為比率逐漸減小以至於『不振動』為止。事實上從自然界中來的一般現象都會比『理論值』更快的到達『停止點』,就像說不只有『動摩擦力』與『靜摩擦力』之區分,摩擦力的『速度相關性』也不是這麼『簡單的正比』之假設,更別說理論上還有著『摩擦生熱』的問題必須要考慮。我們也許可以說為著追求『基本現象的理解』,通常都會『假設』了一些數學上『解答問題』的『理想條件』。
現在談談受外力影響下的受驅振子︰
它的解是
 ,此處相位角
,此處相位角  由
由  所決定。
所決定。
這個系統因為零點時刻突然受到固定大小的外力 所驅動,震盪以
所驅動,震盪以  為比率逐漸增大,一般用
為比率逐漸增大,一般用  為時間尺度來衡量這個變化,每一
為時間尺度來衡量這個變化,每一  單位時間,系統將以
單位時間,系統將以  為比率改變振幅,在物理上稱之為『弛豫時間』Relaxation Time,工程上常用多的
為比率改變振幅,在物理上稱之為『弛豫時間』Relaxation Time,工程上常用多的  單位時間,來談震盪達到預期大小的『安定時間』settling time。果真是『風吹枝擺』,待其風歇『搖曳而止』!!
單位時間,來談震盪達到預期大小的『安定時間』settling time。果真是『風吹枝擺』,待其風歇『搖曳而止』!!
 是驅動力的振幅大小。在線性微分方程式如
是驅動力的振幅大小。在線性微分方程式如  的『求解』裡,如過『
的『求解』裡,如過『 』是
』是  的一個解,『
的一個解,『 』是
』是  一個『特解』,那麼『
一個『特解』,那麼『 』就是該方程是的『通解』。我們已經知道
』就是該方程是的『通解』。我們已經知道  的『低阻尼振子』之解在若干個弛豫時間後數值將變得太小了,所以它對於系統長時間之後的『行為』沒有太多的貢獻。因此我們說這個系統的『穩態解』steady-state solution 是
的『低阻尼振子』之解在若干個弛豫時間後數值將變得太小了,所以它對於系統長時間之後的『行為』沒有太多的貢獻。因此我們說這個系統的『穩態解』steady-state solution 是
 ,此處
,此處

是『響應阻抗』函數。而 是驅動力引發的相位角,可由
是驅動力引發的相位角,可由

所決定,一般它表達著相位『遲滯』 lag 現象。
物理上所說的『慣性』是指一個系統遭受外力時,它會發生『抵抗變化』的作為。這就是『響應阻抗』和『相位遲滯』的物理原由與命名由來。假使考察穩態解,我們是否可以講︰『原因 』── ── 產生成正比之『結果』──
── 產生成正比之『結果』──  ── 的呢??
── 的呢??
─── 部落格訊息︰玩樹莓派, 自得其樂!!───
began with Wieman’s vision to improve the way science is taught and learned. Their stated mission is “To advance science and math literacy and education worldwide through free interactive simulations.”
,按照現今官網的說明
About PhET
PhET provides fun, interactive, research-based simulations of physical phenomena for free. We believe that our research-based approach- incorporating findings from prior research and our own testing- enables students to make connections between real-life phenomena and the underlying science, deepening their understanding and appreciation of the physical world.
…
目前它的線上內容早已經括及多類科學領域,並且很多內容也有了中文的翻譯網頁。作者認為如何用計算機輔助『教育』與『學習』正是今日當有之重要的『學習工具』,實現人們可以用『科學』來解釋『日常生活』中所經驗到的種種『自然現象』的教育宗旨。當你閱讀本文看到有『點擊啟動』的圖片時,請在『點擊啟動』的方形區域外,使用『滑鼠左鍵』點擊圖片的任何位置,進入嵌入式『PhET』線上模擬器的軟體世界。
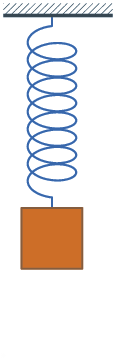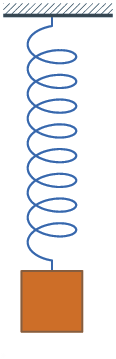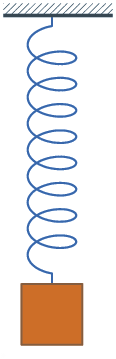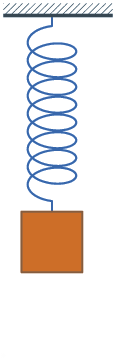
一 個諧振子 harmonic oscillator 是一個物理系統,當它從平衡位置發生位移時,會受到一個正比於位移量  的恢復力
的恢復力  ── 虎克定律──︰
── 虎克定律──︰ ,其中
,其中  是一個正值常數。假使這個系統不受其它的外力影響,通常稱作『簡諧振子』Simple harmonic oscillator;如果此系統同時遭受到與速度成正比的『摩擦力』
是一個正值常數。假使這個系統不受其它的外力影響,通常稱作『簡諧振子』Simple harmonic oscillator;如果此系統同時遭受到與速度成正比的『摩擦力』  ,一般叫做『阻尼振子』Damped harmonic oscillator;要是這個系統還有著跟時間相關的外力
,一般叫做『阻尼振子』Damped harmonic oscillator;要是這個系統還有著跟時間相關的外力  的作用,那麼就稱之為『受驅振子』Driven harmonic oscillators。
的作用,那麼就稱之為『受驅振子』Driven harmonic oscillators。
也就是說簡諧振子是一種『頻率』為
動能 =
由此可以知道簡諧振子的系統總能量是一個常數,這稱之為『能量守恆量』定律,它和『振幅』的平方成正比。它的『頻率』
依據牛頓第二運動定律,一個受驅振子的方程式為
假使
如果我們從
現在談談受外力影響下的受驅振子︰
它的解是
這個系統因為零點時刻突然受到固定大小的外力
是『響應阻抗』函數。而
所決定,一般它表達著相位『遲滯』 lag 現象。
物理上所說的『慣性』是指一個系統遭受外力時,它會發生『抵抗變化』的作為。這就是『響應阻抗』和『相位遲滯』的物理原由與命名由來。假使考察穩態解,我們是否可以講︰『原因 』──
─── 部落格訊息︰玩樹莓派, 自得其樂!!───
【Sonic π】描摹聲音

清‧劉鶚‧《老殘遊記》
《詩經》毛詩序
情發於聲,聲成文謂之音,治世之音安以樂,其政和;亂世之音怨以怒,其政乖;亡國之音哀以思,其民困。故正得失,動天地,感鬼神,莫近於詩。先王以是經夫婦,成孝敬,厚人倫,美教化,移風俗。
風聲雨聲讀書聲雖然都是『聲』,但不知有幾人能詮釋『地籟』之『樂』;或許『誦讀聲』偶然入耳,聽之卻有『弦外之音』。終於『寰宇的振動』一分為三,成為了『自然之聲』、『言語之音』以及『動人之樂』!王小玉說書,字字清晰詞詞明白,音似行雲且聲若流水,一時雷鳴九霄之外,忽而泉湧九地之下,彼音擬樂此聲知音,相追相逐鎔鑄成了『天籟』的聲樂旋律!!


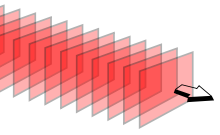
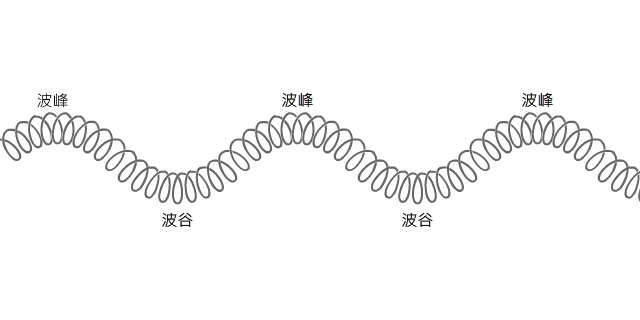
橫波 Transverse wave



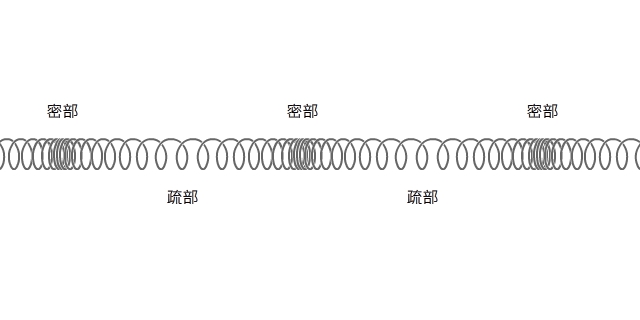
縱波 Longitudinal wave
 www.sandal.tw
www.sandal.tw


波的散射定律 Scattering



波的反射定律 Reflection


波的漫反射 Diffuse reflection

波的折射定律 Refraction





波的繞射 Diffraction 與干涉 Interference


音樂

聲音頻譜

聲音合成器





超聲波影像

依據《後漢書‧天文志》載:『中平二年十月癸亥,客星出南門中,大如半筵,五色喜怒,稍小,至後年六月消』。那一顆『超新星』 ── 天關客星、金牛座  星 ── 於一八五年十二月七日爆炸,在夜空中照耀了八個月,最後變成了今天的『蟹狀星雲』!這星光經過六千五百餘年的時間,穿越太空到達了地球,不知它是否捎來了任何訊息?光是一種『電磁波』,它走的路徑和交互變換的『電磁場』垂直,這在物理上稱作『橫波』 。雖然一根彈撥的『弦』也是『橫波』,在『真空』裡也能『振動』,但這個『弦上波』卻苦於無有『媒介物』medium 可以傳『琴聲』!!
星 ── 於一八五年十二月七日爆炸,在夜空中照耀了八個月,最後變成了今天的『蟹狀星雲』!這星光經過六千五百餘年的時間,穿越太空到達了地球,不知它是否捎來了任何訊息?光是一種『電磁波』,它走的路徑和交互變換的『電磁場』垂直,這在物理上稱作『橫波』 。雖然一根彈撥的『弦』也是『橫波』,在『真空』裡也能『振動』,但這個『弦上波』卻苦於無有『媒介物』medium 可以傳『琴聲』!!
『振動』與『波』的概念其實是難分難解。『振動』可以不是『波』,就是說『它只振動』卻不『擾動周遭』或者『無物可擾』,所以它不產生『波的傳播』。然而『波』主要關注於『擾動傳播』,它可能需要周遭『介質』,因此是一種『 機械波』── 比方,水面波、弦上波 ──,或者可以不需要周遭『介質』,所以不是一種『 機械波』── 就像,引力波、電磁波 ──。但是它的發生總會有一個『擾動源』,在此它與『振動』概念彼此又交織交會。從一個波的『擾動源』或周遭『介質』之『振動方向』與該介質中波的『傳播方向』可以區分兩種關係,一是兩方向『相互垂直』稱做『橫波』Transverse wave,另一是兩方向『相互平行』叫做『縱波』Longitudinal wave。
『聲波』是聲音的『傳播』方式,是一種『機械波』,由物體或聲源『振動』產生,聲波傳播的『媒介空間』一般稱之為『聲場』。它在『氣體』和『液體』介質中傳播時是一種『縱波』,但是在『固體』介質中傳播 時可能會有『橫波』的產生。人類的『耳朵』通常之『聽覺』範圍的『聲波頻率』是在 到
到  之間。事實上自然界中各種生物的聽覺範圍有所不同,比方說『狗』可以聽到高達
之間。事實上自然界中各種生物的聽覺範圍有所不同,比方說『狗』可以聽到高達  的『超聲波』,卻無法聽見
的『超聲波』,卻無法聽見  以下的『重低音』。奇怪乎『波斯的貓』可以聽到 70,000赫茲的超聲波!!
以下的『重低音』。奇怪乎『波斯的貓』可以聽到 70,000赫茲的超聲波!!
既然『聲』也是『波』,所以它就有像『光』一樣的各種『波』的『性質』,然而在日常生活中,『聲光現象』帶給人們的『感覺』卻為什麼又是如此的不同的呢?這主要是因為兩者的『波長』尺度不同所產生的。光速雖快 299,792,458米/秒,然而『可見光』 的部分卻很窄,大約落在波長 0.39 到 0.7 微【 】米之間。這很接近『塵埃』顆粒尺寸範圍,它的直徑通常小於五百微米,小於十微米的懸浮粒子 PM10 ,被認定為有害於人體,小於 2.5 微米的細顆粒物 PM2.5 ,更可以穿透肺泡直達血液。英國物理學家瑞利 Rayleigh 發現當光通過的介質含有『直徑比它的波長小很多』之微小顆粒時會發生『散射』︰
】米之間。這很接近『塵埃』顆粒尺寸範圍,它的直徑通常小於五百微米,小於十微米的懸浮粒子 PM10 ,被認定為有害於人體,小於 2.5 微米的細顆粒物 PM2.5 ,更可以穿透肺泡直達血液。英國物理學家瑞利 Rayleigh 發現當光通過的介質含有『直徑比它的波長小很多』之微小顆粒時會發生『散射』︰
瑞利散射光的強度和入射光波長 的 4次方成反比:
的 4次方成反比:

,其中 是入射光的光強分布函數。
是入射光的光強分布函數。
由於空氣分子的散射,這就是天空常為『藍色』和的太陽常為『黃紅』色調的原因。一九零八年德國物理學家古斯塔夫‧米 Gustav Mie 提出當顆粒尺度相似或大於散射光的波長時,大部分的入射光線會沿著前進的方向進行散射,米式散射的程度跟波長是無關的,而且光散射後的性質也不會改變。因此散射光線會呈現出『白色』或者『灰色』。這就是正午經過太陽照射的雲彩經常會呈現的顏色。
但是一般而言聲音的傳播速度是︰固體 液體
液體  氣體。在乾燥無風的空氣中聲速為
氣體。在乾燥無風的空氣中聲速為  ,在常溫
,在常溫  ℃ 下,空氣中的聲速為 343 米∕秒。因此『可聞聲』之波長範圍在 1.7 公分至 l7 米之間。果真是一者『和光同塵』 ;另一者『暢行無阻』的啊!
℃ 下,空氣中的聲速為 343 米∕秒。因此『可聞聲』之波長範圍在 1.7 公分至 l7 米之間。果真是一者『和光同塵』 ;另一者『暢行無阻』的啊!
當波在來源的介質行進,遭遇到不同之『傳播性質』的另一個介質時,此時它的傳播方向會突然的『改變』,這個回到其來源之介質的現象稱之為『反射』。當波被反射時會遵守反射定律,即『反射角』等於『入射角』 。假使那個『反射界面』不是平滑的,即使原先的波如同『平行光線』,由於各條光線的反射的方向會不同,所以『反射光』就因混亂而『無固定方向』。不要以為這個現象不好,與『位置無關』之均衡的『照明』 和等同的『音量』,正是藉此所產生的。然而『光源』一滅就『四處漆黑』,『呼聲』已過卻能『空谷回響』,這又道說著『聲光』的『不同處』。所謂的『混響』reverberation 正是『聲源』停止後『音聲繼續』迴盪的現象。因此古人所說的『餘音繞樑』果有之哉?!
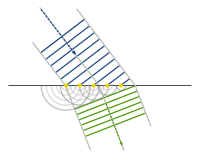
然而有意思的是,波在來源的介質行進,當遭遇到不同之『傳播性質』的另一個介質時,它也可以發生與反射現象『同時』,卻選擇『不回到』其來源的介質之『傳播現象』,這個現象被叫做『折射』。當光在發生折射之時『入射角』與『折射角』符合荷蘭物理學家威理博‧司乃耳 Willebrord Snellius 所提出的折射定律︰
光從第一個介質進入另一不同折射率之第二個介質時,其入射角的正弦 與其『折射率』
與其『折射率』  之乘積會相等:
之乘積會相等:

,這也是『聲光現象』之重要的『差異點』。『光』會被多數『物品』所『阻擋』或可能被『吸收』。以至於很難『穿牆折過』,所謂的『透明性』 ── 比方說玻璃、水晶、瑪瑙,… ──,就是說著『光可透』的這件事。但是相反的俗語說︰需提防『隔牆有耳』 ── 卻講著『聲波』卻是對牆是『視若無睹』,它自能『藉介質振動』而過 ──,所以人們一般才會需要『隔音牆』!更不要說『聲波』的『這個現象』又還能隨著空氣『溫差』之不同,發生『相異』的傳播方向變化,因此聲波『日夜行徑』一般就會有很大的不同的了!!
也許『波動傳播』自然就是『百折不撓』的,就算它的處境已經『無路可走』,只要還能夠找得到『有縫可鑽』,那麼它是否有可能選擇不通過的嗎?這還更別講那個所謂的『隧道效應』之『量子機率波』的了??人們為了分析波的繞射現象,構造了許多『數學模型』來『詮釋』這個現象。現今來說假使它們滿足 ,我們就稱其為『菲涅耳』Fresnel 繞射,它是繞射的『近場近似』;如果它們滿足
,我們就稱其為『菲涅耳』Fresnel 繞射,它是繞射的『近場近似』;如果它們滿足  ,我們就稱其為『夫琅禾費』Fraunhofer 繞射,它是繞射的『遠場近似』。這裡的
,我們就稱其為『夫琅禾費』Fraunhofer 繞射,它是繞射的『遠場近似』。這裡的  就是那個『縫』或『孔』的尺寸;
就是那個『縫』或『孔』的尺寸;  是孔徑與觀察屏的距離。
是孔徑與觀察屏的距離。
假使換個角度從頻率上看,最早被人們所認識的聲波當然是人耳能夠聽到的『可聞音』,這可關係到了『語言』、『音樂』、『樂器』、『空間音質』與『噪音』等等,它們分别對應著『語言聲學』、『音樂聲學』、『樂器聲學』、『聲場聲學』以及『噪音控制』種種。然後又及於『聽覺』的『生理、心理聲學』,並隨著一八八零年法國物理學家皮埃爾‧居禮 Pierre Curie 和雅克‧居禮 Jacques Curie 兄弟發現『電氣石』具有『壓電效應』,開啟了聲波頻率超過 的『超聲波』之大門。當聲波頻率再超過
的『超聲波』之大門。當聲波頻率再超過  稱為『特超聲』,它的『波長』已經可以與『分子』大小相比擬,它的研究就叫做『分子聲學』。反過來講當聲波頻率低於
稱為『特超聲』,它的『波長』已經可以與『分子』大小相比擬,它的研究就叫做『分子聲學』。反過來講當聲波頻率低於  有『次聲學』,用以研究『火山爆發』或者『流星爆炸』所產生的『聲重力波』。也可以說『物理聲學』正與眾多學科領越交叉融會,匯聚成洋洋大觀的『科技前延』,果真是既古又新的啊 !!
有『次聲學』,用以研究『火山爆發』或者『流星爆炸』所產生的『聲重力波』。也可以說『物理聲學』正與眾多學科領越交叉融會,匯聚成洋洋大觀的『科技前延』,果真是既古又新的啊 !!
然而電子『聲音合成器』的發展歷史雖不可能早於一八二七年德國物理學家蓋歐格‧西蒙‧歐姆 Georg Simon Ohm 在《直流電路的數學研究》一文中『歐姆定律』的發表,如今卻已經很難追遡!現今所說的『合成器』Synthesizer,是利用多種『電子技術』 ── 比方說,加法合成、減法合成、FM、相位調變…──,或者使用『物理模型』發聲的『電子樂器』── 也常稱作鍵盤樂器 ──。
『Sonic π』的發聲軟體的核心就是一種『軟體合成器』,使用樹莓派『模擬』了二十三種『聲音合成』的方式,採用『樂器數位介面』MIDI Musical Instrument Digital Interface 的描述碼來表達『音符』。同時這個軟體合成器對於一個『聲音』的發聲控制,採取了一般常用的『ADSR』Attack-Decay-Sustain-Release 波封機制。
『振動』與『波』的概念其實是難分難解。『振動』可以不是『波』,就是說『它只振動』卻不『擾動周遭』或者『無物可擾』,所以它不產生『波的傳播』。然而『波』主要關注於『擾動傳播』,它可能需要周遭『介質』,因此是一種『 機械波』── 比方,水面波、弦上波 ──,或者可以不需要周遭『介質』,所以不是一種『 機械波』── 就像,引力波、電磁波 ──。但是它的發生總會有一個『擾動源』,在此它與『振動』概念彼此又交織交會。從一個波的『擾動源』或周遭『介質』之『振動方向』與該介質中波的『傳播方向』可以區分兩種關係,一是兩方向『相互垂直』稱做『橫波』Transverse wave,另一是兩方向『相互平行』叫做『縱波』Longitudinal wave。
『聲波』是聲音的『傳播』方式,是一種『機械波』,由物體或聲源『振動』產生,聲波傳播的『媒介空間』一般稱之為『聲場』。它在『氣體』和『液體』介質中傳播時是一種『縱波』,但是在『固體』介質中傳播 時可能會有『橫波』的產生。人類的『耳朵』通常之『聽覺』範圍的『聲波頻率』是在
既然『聲』也是『波』,所以它就有像『光』一樣的各種『波』的『性質』,然而在日常生活中,『聲光現象』帶給人們的『感覺』卻為什麼又是如此的不同的呢?這主要是因為兩者的『波長』尺度不同所產生的。光速雖快 299,792,458米/秒,然而『可見光』 的部分卻很窄,大約落在波長 0.39 到 0.7 微【
瑞利散射光的強度和入射光波長
,其中
由於空氣分子的散射,這就是天空常為『藍色』和的太陽常為『黃紅』色調的原因。一九零八年德國物理學家古斯塔夫‧米 Gustav Mie 提出當顆粒尺度相似或大於散射光的波長時,大部分的入射光線會沿著前進的方向進行散射,米式散射的程度跟波長是無關的,而且光散射後的性質也不會改變。因此散射光線會呈現出『白色』或者『灰色』。這就是正午經過太陽照射的雲彩經常會呈現的顏色。
但是一般而言聲音的傳播速度是︰固體
當波在來源的介質行進,遭遇到不同之『傳播性質』的另一個介質時,此時它的傳播方向會突然的『改變』,這個回到其來源之介質的現象稱之為『反射』。當波被反射時會遵守反射定律,即『反射角』等於『入射角』 。假使那個『反射界面』不是平滑的,即使原先的波如同『平行光線』,由於各條光線的反射的方向會不同,所以『反射光』就因混亂而『無固定方向』。不要以為這個現象不好,與『位置無關』之均衡的『照明』 和等同的『音量』,正是藉此所產生的。然而『光源』一滅就『四處漆黑』,『呼聲』已過卻能『空谷回響』,這又道說著『聲光』的『不同處』。所謂的『混響』reverberation 正是『聲源』停止後『音聲繼續』迴盪的現象。因此古人所說的『餘音繞樑』果有之哉?!
然而有意思的是,波在來源的介質行進,當遭遇到不同之『傳播性質』的另一個介質時,它也可以發生與反射現象『同時』,卻選擇『不回到』其來源的介質之『傳播現象』,這個現象被叫做『折射』。當光在發生折射之時『入射角』與『折射角』符合荷蘭物理學家威理博‧司乃耳 Willebrord Snellius 所提出的折射定律︰
光從第一個介質進入另一不同折射率之第二個介質時,其入射角的正弦
,這也是『聲光現象』之重要的『差異點』。『光』會被多數『物品』所『阻擋』或可能被『吸收』。以至於很難『穿牆折過』,所謂的『透明性』 ── 比方說玻璃、水晶、瑪瑙,… ──,就是說著『光可透』的這件事。但是相反的俗語說︰需提防『隔牆有耳』 ── 卻講著『聲波』卻是對牆是『視若無睹』,它自能『藉介質振動』而過 ──,所以人們一般才會需要『隔音牆』!更不要說『聲波』的『這個現象』又還能隨著空氣『溫差』之不同,發生『相異』的傳播方向變化,因此聲波『日夜行徑』一般就會有很大的不同的了!!
也許『波動傳播』自然就是『百折不撓』的,就算它的處境已經『無路可走』,只要還能夠找得到『有縫可鑽』,那麼它是否有可能選擇不通過的嗎?這還更別講那個所謂的『隧道效應』之『量子機率波』的了??人們為了分析波的繞射現象,構造了許多『數學模型』來『詮釋』這個現象。現今來說假使它們滿足
假使換個角度從頻率上看,最早被人們所認識的聲波當然是人耳能夠聽到的『可聞音』,這可關係到了『語言』、『音樂』、『樂器』、『空間音質』與『噪音』等等,它們分别對應著『語言聲學』、『音樂聲學』、『樂器聲學』、『聲場聲學』以及『噪音控制』種種。然後又及於『聽覺』的『生理、心理聲學』,並隨著一八八零年法國物理學家皮埃爾‧居禮 Pierre Curie 和雅克‧居禮 Jacques Curie 兄弟發現『電氣石』具有『壓電效應』,開啟了聲波頻率超過
然而電子『聲音合成器』的發展歷史雖不可能早於一八二七年德國物理學家蓋歐格‧西蒙‧歐姆 Georg Simon Ohm 在《直流電路的數學研究》一文中『歐姆定律』的發表,如今卻已經很難追遡!現今所說的『合成器』Synthesizer,是利用多種『電子技術』 ── 比方說,加法合成、減法合成、FM、相位調變…──,或者使用『物理模型』發聲的『電子樂器』── 也常稱作鍵盤樂器 ──。
『Sonic π』的發聲軟體的核心就是一種『軟體合成器』,使用樹莓派『模擬』了二十三種『聲音合成』的方式,採用『樂器數位介面』MIDI Musical Instrument Digital Interface 的描述碼來表達『音符』。同時這個軟體合成器對於一個『聲音』的發聲控制,採取了一般常用的『ADSR』Attack-Decay-Sustain-Release 波封機制。
f(x)=sin2x f'(x)=(sin2x)'=(2sinxcosx)=2cosxcosx+2sinx(-sinx)=2(cos²x-sin²x)=2cos2x
追问
f'(x)=(sin2x)'=(2sinxcosx) 这一步怎么得来的? =2cosxcosx+2sinx(-sinx)然后还有这一步 =2(cos²x-sin²x)=2cos2x 然后还有这一步 麻烦给解释下,数学基础不太好
回答
(sinx)'=cosx (cosx)'=-sinx (nx)'=n [u(x)v(x)]'=(u'(x)v(x)+u(x)v'(x) sin2x=sin(x+x)=sinxcosx+sinxcosx=2sinxcosx f(x)=sin2x=2sinxcosx f'(x)=(2sinxcosx)'=(2sinx)'cosx+(2sinx)(cosx)'=2cosxcosx-2sinxsinx=2cos²x-2sin²x =2(cos²x-sin²x) cos2x=cos(x+x)=cosxcosx-sinxsinx=cos²x-sin²x
【小卒个人文集】从“拉普拉斯算符的本质”去理解波函数的动能,顺便埋汰“节点理论”
从“拉普拉斯算符的本质”去理解波函数的动能,顺便埋汰“节点理论”
密度泛函·小卒
2010.04.26
从本科我们第一次接触《物质结构》这门必修课,我们就学到了薛定谔方程HΨ=EΨ。式中,哈密顿算符H定义为动能项T和势能项V的线性组合。在动能项T中引入了拉普拉斯算符 。从这时候开始,拉普拉斯算符
。从这时候开始,拉普拉斯算符 就与我们结下了不解之缘。(做理论的人都是咬牙切齿说出这句话的,那个恨啊)
就与我们结下了不解之缘。(做理论的人都是咬牙切齿说出这句话的,那个恨啊)
由公式 我们可以计算波的动能。根据公式
我们可以计算波的动能。根据公式 ,E虽然是对全空间进行积分,但是由于拉普拉斯算符是二阶微商,它给出的是波函数在特定位置的梯度的变化率(就是变化速度的变化速度)。因此,波的动能就是动能在全空间的平均值,也就是波函数梯度的平均变化率。
,E虽然是对全空间进行积分,但是由于拉普拉斯算符是二阶微商,它给出的是波函数在特定位置的梯度的变化率(就是变化速度的变化速度)。因此,波的动能就是动能在全空间的平均值,也就是波函数梯度的平均变化率。
我们先看一个宏观现象:一维正弦波。我们用图1表示一维正弦波f1(x)=sinx,f2(x)=sin2x,和f3(x)=2sinx。

我们计算它们的二阶微分,分别是f1"=-sinx,f2"=-4sin2x,和f3"=-2sinx。于是我们可以看到,正弦波f1的动能低于f2的原因在于“f1频率低”,正弦波f1的动能低于f3的原因在于“f1振幅低”。在量子化学领域,振幅已经不再是一个确定的量。或者说,在量子化学看来,f1和f3是同一个波。现在关键问题集中到了f1与f2的比较上。由于f2的波形改变的速度(波形坡度的变化)比f1要快,所以f2获得了更高的平均动能。

自然界有一个普适原理,即能量最低原理。这里再举一个很简单的例子,一维无限深势阱的粒子运动,波以恒定的频率在整个空间内传播,在势阱内各个区域,该粒子的波形处处相同。再延伸一下,如果这个一维无限深势阱的长度是无限的,那么随着波的传播,波的动能将趋近于零。但是在有原子核存在的情况下,电子和原子核之间有束缚力。这种“原子核对电子的束缚力”和“电子动能向空间的衰减”之间存在一个平衡。说到这里,我们终于开始接近稍微实际一点儿的物理图景了。比如我们来看两个一维GTO波形,分别是GTO1=exp(-x^2)和GTO2=(1/2)exp(-0.25x^2),如图2。

对这两个GTO波形做二阶微分,得到GTO1"=-2*Exp(-x^2)+4*x^2*Exp(-x^2),GTO2"=-1/4*Exp(-1/4*x^2)+1/8*x^2*Exp(-1/4*x^2),如图3。

此时,我们可以说,GTO1的动能高于GTO2。电子会优先占据能量低的轨道,这就是能量最低原理的普适性。
写到这里,我不禁想起了害死人的“节点理论”。我们在有机化学中学到的节点理论,说的是“节点越多,轨道能量越高”。后来我学了理论化学之后,怎么想都不是这个事儿,纠结啊。其实粗粗一想,也是啊,在单位空间内,波函的相位改变次数越多(也就是所谓的“节点越多”),那么能量越高,很符合上面的讨论啊。写到这里,我突然发现,节点理论说的只是动能。标准的哈密顿量H是由五项组成的,分别是核动能、电子动能、核-核斥力、电子-电子斥力、电子-核引力。我在刚才分析动能的时候,已经不自觉的使用了波恩-奥本海默的定核近似了(忽略核动能)。而这个节点理论可比我过分多了,人家只考虑了电子动能,将核-核斥力、电子-电子斥力、电子-核引力一律忽略。这忽略也太狠了,毕竟E = <Ψ|H|Ψ>/<Ψ|Ψ> = <Ψ|T+V|Ψ>/<Ψ|Ψ> = <Ψ|T|Ψ>/<Ψ|Ψ> + <Ψ|V|Ψ>/<Ψ|Ψ> ,而节点理论完全忽略了势能项<Ψ|V|Ψ>/<Ψ|Ψ>!好吧,在同一个分子之中,核-核斥力可以看做固定的,忽略了也没啥,关键是电子-电子斥力、电子-核引力这两项被忽略是实在说不过去的。因此,在普通量子化学计算中,大家会发现,节点理论经常失效,节点少的某些轨道能量反而是高的。
所以,大家本科时候虽然都学了节点理论,现在既然做了理论化学,咱们就忘掉节点理论吧。……呃,要不,我还是老老实实承认吧:我其实就是来故意埋汰节点理论的,这才是我的真正目的,啊哈哈哈!
全部公式都是用盗版的MathType6.7写的,导出为gif文件。
全部图像都是用免费版的SpeQ3.4画的,用截屏的方式存jpg。
哈哈,都很原始的哦
一天后补充:cenwanglai区长提意见说“把GTO1和GTO2用拉布拉斯算符处理一下,再画图,再来比较讨论,全文是不是更统一呢”,大善,立即修改!感谢cenwanglai区长
密度泛函·小卒
2010.04.26
从本科我们第一次接触《物质结构》这门必修课,我们就学到了薛定谔方程HΨ=EΨ。式中,哈密顿算符H定义为动能项T和势能项V的线性组合。在动能项T中引入了拉普拉斯算符
 。从这时候开始,拉普拉斯算符
。从这时候开始,拉普拉斯算符 就与我们结下了不解之缘。(做理论的人都是咬牙切齿说出这句话的,那个恨啊)
就与我们结下了不解之缘。(做理论的人都是咬牙切齿说出这句话的,那个恨啊)由公式
 我们可以计算波的动能。根据公式
我们可以计算波的动能。根据公式 ,E虽然是对全空间进行积分,但是由于拉普拉斯算符是二阶微商,它给出的是波函数在特定位置的梯度的变化率(就是变化速度的变化速度)。因此,波的动能就是动能在全空间的平均值,也就是波函数梯度的平均变化率。
,E虽然是对全空间进行积分,但是由于拉普拉斯算符是二阶微商,它给出的是波函数在特定位置的梯度的变化率(就是变化速度的变化速度)。因此,波的动能就是动能在全空间的平均值,也就是波函数梯度的平均变化率。我们先看一个宏观现象:一维正弦波。我们用图1表示一维正弦波f1(x)=sinx,f2(x)=sin2x,和f3(x)=2sinx。

我们计算它们的二阶微分,分别是f1"=-sinx,f2"=-4sin2x,和f3"=-2sinx。于是我们可以看到,正弦波f1的动能低于f2的原因在于“f1频率低”,正弦波f1的动能低于f3的原因在于“f1振幅低”。在量子化学领域,振幅已经不再是一个确定的量。或者说,在量子化学看来,f1和f3是同一个波。现在关键问题集中到了f1与f2的比较上。由于f2的波形改变的速度(波形坡度的变化)比f1要快,所以f2获得了更高的平均动能。

自然界有一个普适原理,即能量最低原理。这里再举一个很简单的例子,一维无限深势阱的粒子运动,波以恒定的频率在整个空间内传播,在势阱内各个区域,该粒子的波形处处相同。再延伸一下,如果这个一维无限深势阱的长度是无限的,那么随着波的传播,波的动能将趋近于零。但是在有原子核存在的情况下,电子和原子核之间有束缚力。这种“原子核对电子的束缚力”和“电子动能向空间的衰减”之间存在一个平衡。说到这里,我们终于开始接近稍微实际一点儿的物理图景了。比如我们来看两个一维GTO波形,分别是GTO1=exp(-x^2)和GTO2=(1/2)exp(-0.25x^2),如图2。

对这两个GTO波形做二阶微分,得到GTO1"=-2*Exp(-x^2)+4*x^2*Exp(-x^2),GTO2"=-1/4*Exp(-1/4*x^2)+1/8*x^2*Exp(-1/4*x^2),如图3。

此时,我们可以说,GTO1的动能高于GTO2。电子会优先占据能量低的轨道,这就是能量最低原理的普适性。
写到这里,我不禁想起了害死人的“节点理论”。我们在有机化学中学到的节点理论,说的是“节点越多,轨道能量越高”。后来我学了理论化学之后,怎么想都不是这个事儿,纠结啊。其实粗粗一想,也是啊,在单位空间内,波函的相位改变次数越多(也就是所谓的“节点越多”),那么能量越高,很符合上面的讨论啊。写到这里,我突然发现,节点理论说的只是动能。标准的哈密顿量H是由五项组成的,分别是核动能、电子动能、核-核斥力、电子-电子斥力、电子-核引力。我在刚才分析动能的时候,已经不自觉的使用了波恩-奥本海默的定核近似了(忽略核动能)。而这个节点理论可比我过分多了,人家只考虑了电子动能,将核-核斥力、电子-电子斥力、电子-核引力一律忽略。这忽略也太狠了,毕竟E = <Ψ|H|Ψ>/<Ψ|Ψ> = <Ψ|T+V|Ψ>/<Ψ|Ψ> = <Ψ|T|Ψ>/<Ψ|Ψ> + <Ψ|V|Ψ>/<Ψ|Ψ> ,而节点理论完全忽略了势能项<Ψ|V|Ψ>/<Ψ|Ψ>!好吧,在同一个分子之中,核-核斥力可以看做固定的,忽略了也没啥,关键是电子-电子斥力、电子-核引力这两项被忽略是实在说不过去的。因此,在普通量子化学计算中,大家会发现,节点理论经常失效,节点少的某些轨道能量反而是高的。
所以,大家本科时候虽然都学了节点理论,现在既然做了理论化学,咱们就忘掉节点理论吧。……呃,要不,我还是老老实实承认吧:我其实就是来故意埋汰节点理论的,这才是我的真正目的,啊哈哈哈!
全部公式都是用盗版的MathType6.7写的,导出为gif文件。
全部图像都是用免费版的SpeQ3.4画的,用截屏的方式存jpg。
哈哈,都很原始的哦
一天后补充:cenwanglai区长提意见说“把GTO1和GTO2用拉布拉斯算符处理一下,再画图,再来比较讨论,全文是不是更统一呢”,大善,立即修改!感谢cenwanglai区长
学习
顶一个
顶一个
公式要用LaTex咯。那才是小卒风采。
有点意思哈。
不错。支持一下
把GTO1和GTO2用拉布拉斯算符处理一下,再画图,再来比较讨论,全文是不是更统一呢?
你哪句话把节点理论给驳倒了?
Originally posted by yjcmwgk at 2011-04-26 21:24:29:
从“拉普拉斯算符的本质”去理解波函数的动能,顺便埋汰“节点理论”
密度泛函·小卒
2010.04.26
从本科我们第一 ...
1. 想必楼主看原文有误,我记得“节点”问题只是说,在同一个原子的一系列原子轨道中,节点越多的轨道能量越高。在同一个原子的同一套波函数中,就没有Exp和Exp的不同,指数部分都是Exp,区别只是在别的部分,比如2s轨道是乘上一个(2-x)之类。从“拉普拉斯算符的本质”去理解波函数的动能,顺便埋汰“节点理论”
密度泛函·小卒
2010.04.26
从本科我们第一 ...
2. 而且“节点说”只是一个经验规律,只是从波函数的形式看出来的。
而且原子轨道是Slater函数而不是Gauss函数,楼主要不要画画Slater函数看看啊?
3. 根据维里定理,原子系统中的电子的动能精确等于1/2总能量。没必要把势能算出来。徐光宪爷爷的书,楼主没好好看吧?:D
好吧,从一楼开始我就没明白过...一定是我的打开方式不对...
建议文章在开头先把“节点理论”的定义阐述清楚,讨论适用条件。否则节点理论是什么没有明确的话,所谓的“埋汰”就无从谈起。
与其用正弦波、GTO这样和分子轨道、原子轨道没有直接关系的函数来讨论,我建议加入一些实际分子轨道波函数的讨论,比如共轭长链烯烃、苯的前线轨道等等,这才是节点定理最经常拿来说事的情况。把量化程序输出的轨道动能、势能和分子轨道图形相互对照讨论是有益的。(动能密度可以通过Multiwfn等程序计算和绘制,也可以一起讨论)
节点定理是经验规则,在它所适合的条件下是不错的能量判断方法。与其说将节点定理“埋汰”掉,我认为本文主题应改为讨论节点定理的使用误区。找几个有决定性的反例,比如苯的能量最低的pi轨道(仅分子平面一个节点)就比一些带有多个节面的sigma特征的轨道能量要高。
另外文中在讨论动能时忽视了一个问题,尽管不影响定性结论。也就是轨道的哈密顿动能=-1/2∫ψ(r)* ▽^2 ψ(r)dr,文中只用轨道波函数的二阶导数讨论问题,即▽^2 ψ(r)这部分,然而积分元中还有一个ψ(r)*却被忽视了,它在积分中起到了“权重”作用。还有一点,就是积分当中的负号,讨论GTO1、2的动能时候,忽略掉负号从图中看只会得到相反的结论。
即便修正了正负号问题,从图3上看GTO1、2的关系仍不是那么清楚,GTO1正值区域大负值区域也大,GTO2正值区域小负值区域也小,相互抵消后谁大谁小就不易直观判断了。这正是这种所谓的“哈密顿”动能密度的定义的缺陷,局部动能有的地方为负值违背了一般物理直觉。我建议绘制拉格朗日动能密度图形,由于处处为正,容易看出积分出来谁大谁小。
与其用正弦波、GTO这样和分子轨道、原子轨道没有直接关系的函数来讨论,我建议加入一些实际分子轨道波函数的讨论,比如共轭长链烯烃、苯的前线轨道等等,这才是节点定理最经常拿来说事的情况。把量化程序输出的轨道动能、势能和分子轨道图形相互对照讨论是有益的。(动能密度可以通过Multiwfn等程序计算和绘制,也可以一起讨论)
节点定理是经验规则,在它所适合的条件下是不错的能量判断方法。与其说将节点定理“埋汰”掉,我认为本文主题应改为讨论节点定理的使用误区。找几个有决定性的反例,比如苯的能量最低的pi轨道(仅分子平面一个节点)就比一些带有多个节面的sigma特征的轨道能量要高。
另外文中在讨论动能时忽视了一个问题,尽管不影响定性结论。也就是轨道的哈密顿动能=-1/2∫ψ(r)* ▽^2 ψ(r)dr,文中只用轨道波函数的二阶导数讨论问题,即▽^2 ψ(r)这部分,然而积分元中还有一个ψ(r)*却被忽视了,它在积分中起到了“权重”作用。还有一点,就是积分当中的负号,讨论GTO1、2的动能时候,忽略掉负号从图中看只会得到相反的结论。
即便修正了正负号问题,从图3上看GTO1、2的关系仍不是那么清楚,GTO1正值区域大负值区域也大,GTO2正值区域小负值区域也小,相互抵消后谁大谁小就不易直观判断了。这正是这种所谓的“哈密顿”动能密度的定义的缺陷,局部动能有的地方为负值违背了一般物理直觉。我建议绘制拉格朗日动能密度图形,由于处处为正,容易看出积分出来谁大谁小。
请问, 标题下面的日期是不是写错了...
nnd
反正我是一点看不懂:rol:
反正我是一点看不懂:rol:
牛X,完全看不懂的路过。。。:cry:
不确定您说的是哪种节点理论。如果是指一个算符的第N个本征函数,在它的边界内部有N-1个零点/线/面/...,这是Sturm-Liouville型常微分方程的一个严格结果,对于更一般的情况(高维,多变量...)并没有这么强的结论。参见Hilbert&Courant, methods of mathematical physics第六章第六节
在量子力学中,一维无穷深势阱的能级自基态动能增加;而按virial定理,氢原子1s,2s,3s...态的动能减少,势能增加,总能量上升。所以节点可以对应动能的增加和减少,都可以提升总能量。
在量子力学中,一维无穷深势阱的能级自基态动能增加;而按virial定理,氢原子1s,2s,3s...态的动能减少,势能增加,总能量上升。所以节点可以对应动能的增加和减少,都可以提升总能量。
羡慕大家! 真厉害 与其望洋兴叹 不如看点基础知识 补补课
 or 2
or 2 in this case where r = 1.
in this case where r = 1.
In other words the unit circle, which spans an angle of 360°, has a circumference of 2 .
.
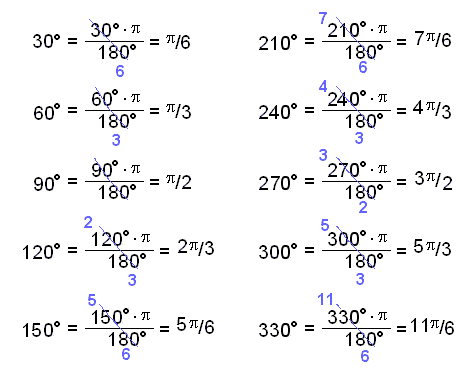
To do this we have to multiply by 180/ , using the value for
, using the value for  on the calculator ≈ 3.14
on the calculator ≈ 3.14
1∙180°/ ≈ 57.3°
≈ 57.3°
 /4 radians to degrees.
/4 radians to degrees.
Again we can multiply by 180/ or use the fact that p radians is the same as 180°. So we can simply replace
or use the fact that p radians is the same as 180°. So we can simply replace  by 180°.
by 180°.
5 /4 = 5∙180/4 = 225°.
/4 = 5∙180/4 = 225°.

It’s very easy to draw graphs of trig functions if a graphical calculator is used.
The following describes how to do this with a CASIO calculator. The first thing to do is to decide in what units the angle is to be measured. The calculator offers three possibilities. Degrees, radians and grads.
Grads are similar to degrees but with 400 grads in a circle rather than 360°.
The units are changed by choosing the graph on the menu and then pressing

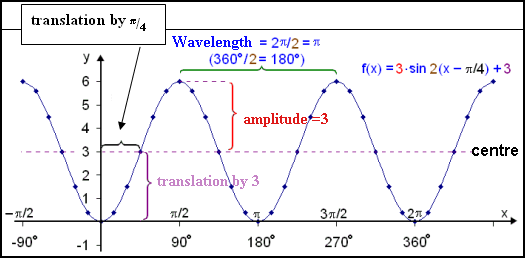
 /4) + 3 and compare to the basic function f(x) = sin x.
/4) + 3 and compare to the basic function f(x) = sin x.
a = p/4, which means that the wave has been translated by /4 (45°) to the right .
/4 (45°) to the right .
e = 3 so the wave has been translated 3 units vertically up.
b = 2 so the period is 2 /2 =
/2 =  .
.
c = 3 so the amplitude of the wave is 3.
Now we’ll use this information to draw the graph.
 /2 (90°), 3
/2 (90°), 3 /2 and so on at intervals of
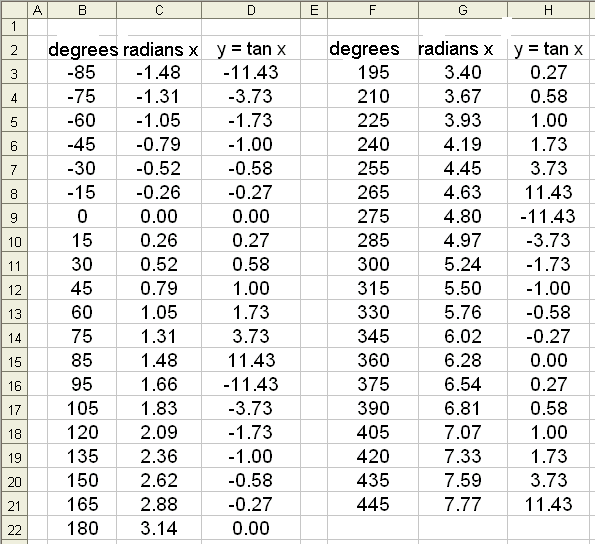
/2 and so on at intervals of  units (180°). The following is a table of values from Excel. We have left out the values of x where tan x does not exist, that is where the asymptotes are.
units (180°). The following is a table of values from Excel. We have left out the values of x where tan x does not exist, that is where the asymptotes are.
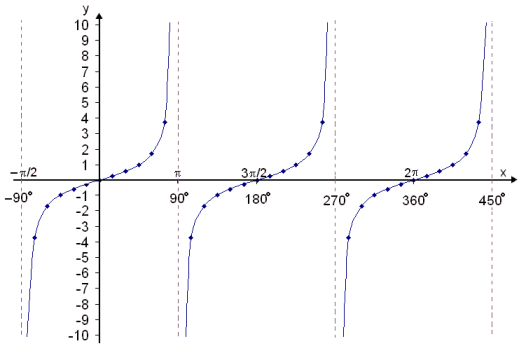
The tangent function is always increasing ( goes up as we move to the right ).
It is steep near to the asymptote in x = − /2 (−90°).
/2 (−90°).
The function takes the value −1 when x = − /4 (−45°) and 0 when
/4 (−45°) and 0 when
x = 0. It then takes the value 1 in x = /4 (45°) and rises rapidly as x gets near to the value x =
/4 (45°) and rises rapidly as x gets near to the value x =  /2 (90°) where there is another asymptote. This curve repeats itself at intervals of
/2 (90°) where there is another asymptote. This curve repeats itself at intervals of  or 180° which is the period of the function.
or 180° which is the period of the function.
Try Quiz 3 on Trig functions.
Remember to use the checklist to keep track of your work.
© 2008 Rasmus ehf and Jóhann Ísak
| Trig functions |
Lesson 3 Graphs of trig functions
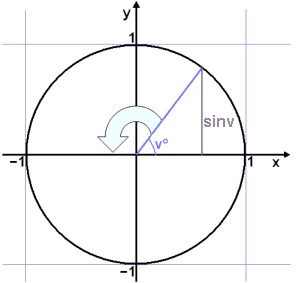
We will now look at the graphs of trig functions starting with the function f(v°) = sin v°. The angle v° is measured from the x– axis and we look at what happens as the angle v gets bigger.

We make a table of values:
We have already calculated sin 30° and sin 60° by using the fact that in triangles with angles 30°, 60° and 90°, the side opposite the 30° angle is half the length of the hypotenuse. This means we can easily find values of sin v° at 30° intervals. We can also use the sin x function in the calculator or the spread sheet.
v°
|
f(v°) = sin v°
| |
| 0° | 0 | 0 |
| 30° |
1/2
| 0.5 |
| 60° | 0.866 | |
| 90° | 1 | 1 |
| 120° | 0.866 | |
| 150° | 1/2 | 0.5 |
| 180° | 0 | 0 |
| 210° |
-1/2
| -0.5 |
| 240° |
-
| -0.866 |
| 270° | -1 | -1 |
| 300° | - | -0.866 |
| 330° | -1/2 | -0.5 |
| 360° | 0 | 0 |
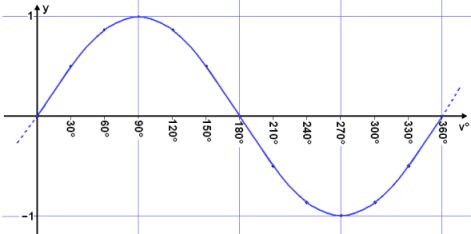
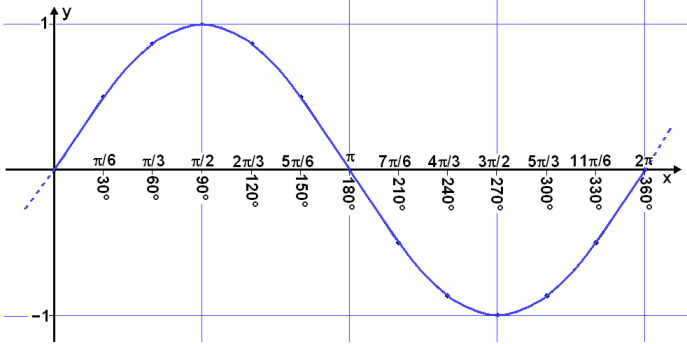
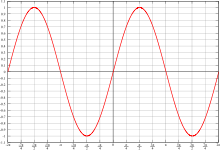
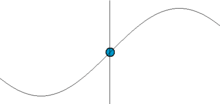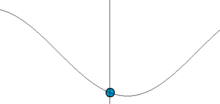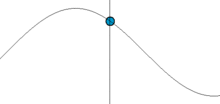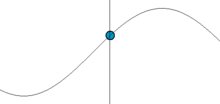
Now we draw a graph from these values, marking the angles v° on the x – axis and sin v° on the y – axis .

The result is the Sine wave, a well known phenomena in physics and the natural sciences. The problem is that Sine waves in nature are functions of time and length, not degrees, as we have used here.
To solve this problem a new way of measuring angles is used. This unit for measuring an angle is called a Radian and is found by measuring the length of the arc of the unit circle between the radius that forms one side of the angle and the x – axis.
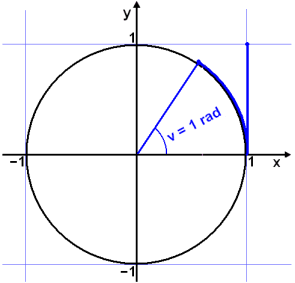
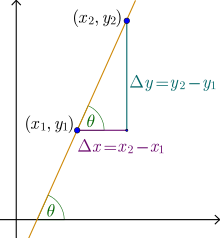
One radian is the size of an angle that sweeps out an arc of length one unit on the unit circle ( see diagram ).

Imagine putting a wire of the same length as the radius, at the point on the x – axis where x = 1. Now bend the wire round the circumference of the circle. The angle at the centre of the circle that spans this arc is one radian. The unit is sometimes called rad. Can you see from the diagram that 1 rad is slightly less than 60°?.
But how do we find the exact connection between degrees and radians? How can we change between degrees and radians?
We do this by noting that the circumference of a circle is 2∙r∙In other words the unit circle, which spans an angle of 360°, has a circumference of 2
This leads to the following result:
| 2 |
| To change from radians to degrees we multiply by 180/ |
| To change from degrees to radians we multiply by |
Example 1
We’ll now look at the Sine wave in our usual x – y coordinate system.
To do this we need to change the angles from degrees to radians by multiplying by  /180 and cancelling as much as possible.
/180 and cancelling as much as possible.
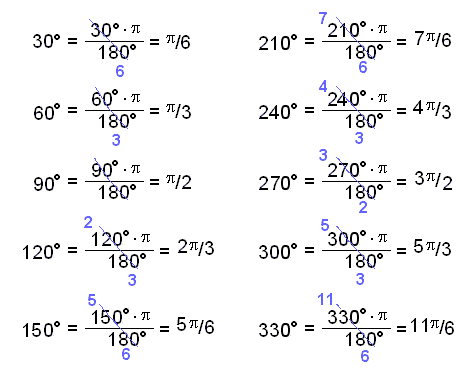
Now we put the angles in radians as values on the x – axis. We’ll leave the degrees in as well for comparison.

Example 2
Calculate the number of degrees in one radian.To do this we have to multiply by 180/
1∙180°/
Example 3
Change 5Again we can multiply by 180/
5

It’s very easy to draw graphs of trig functions if a graphical calculator is used.
The following describes how to do this with a CASIO calculator. The first thing to do is to decide in what units the angle is to be measured. The calculator offers three possibilities. Degrees, radians and grads.
Grads are similar to degrees but with 400 grads in a circle rather than 360°.
The units are changed by choosing the graph on the menu and then pressing
„Shift and Set Up“.
The window that opens offers various possibilities, but for the moment we are only concerned with angle measurement. Use the arrows on the calculator and go to
„Angle“.
The following three choices can be made:
„Deg, Rad, Gra“
By pressing F1, F2 or F3.
We choose either “Deg”(degrees) or ”Rad” (radians) and press “exe”.
Next we choose the scale on the x axis by pressing
Shift og View Window (F3) and choosing “trig” (F2)
Now we are ready to draw the graph.

For example the graph of y = sin x

Now we can draw the graph by pressing F6 .
Example 4
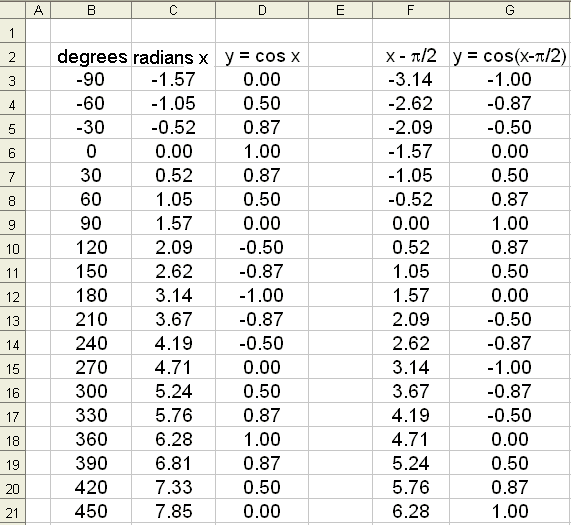
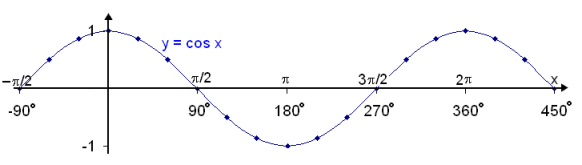
We will now see how Excel can be used to draw some trig graphs. First we will draw the graph of f(x) = cos x, for x on the interval −90° to 450° and find values of cos x at 30° intervals. We start by entering −90 in the column for angles (B3) then −60 and so on. ( It’s best to do this by copying down)
Excel uses radians so we use column C for the radian values of the angles. This is done by multiplying by  /180. The formula in C3 will be =B3*Pi()/180. The formula is then copied down the C column.
/180. The formula in C3 will be =B3*Pi()/180. The formula is then copied down the C column.
We put the formula for the cosine function in column D. The formula in D3 will be =cos(C3) . Again it can be copied down the column.
The graph is drawn by blocking columns B and D, choosing the graphing tool and then XY (scatter). The appearance of the graph can be changed by right clicking with the mouse. The Excel spread sheet will look as follows:

The graph y = cos x looks like this:

We see that the cosine graph is exactly the same as the sine graph if it is moved by by  /2 (90°) to the right.
/2 (90°) to the right.
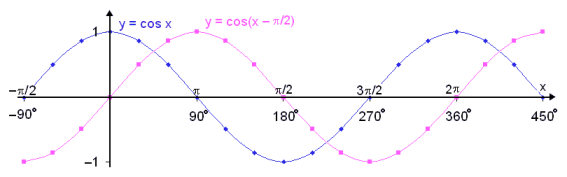
See what happens if we subtract  /2 from the values in column C and find the cosine of the new values. (see columns F– G), then draw the graph of y = cos(x −
/2 from the values in column C and find the cosine of the new values. (see columns F– G), then draw the graph of y = cos(x −  /2).
/2).

In this way we have translated the cosine graph by /2 (90°) to the right and the result is the graph of the sine function.
/2 (90°) to the right and the result is the graph of the sine function.
This shows that the following rule holds:
This shows that the following rule holds:
sin x = cos(x −  /2)
/2)
The following general rule is true:
The graphs of the trig functions can be translated to the right by subtracting a constant value from the variable x.
The graphs of y = sin(x − a) and y = cos(x − a) are the same as the graphs of y = sin x and
y = cos x translated by a units. The translation is to the right if a > 0 and to the left if a < 0. |
If a is negative we get two negatives and are therefore adding to the x value. This is equivalent to a translation to the left. We can also say that the graph y = cos(x + b) is the same as the graph of y = cos x translated b units to the left.
Example 5
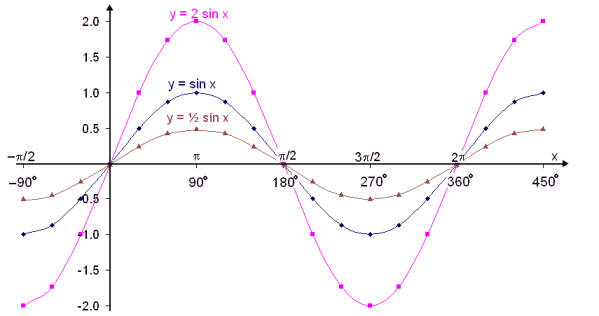
We will now use Excel to see the effect that multiplying the sine function by a constant number has on the graph.
We’ll look at the graphs of y = sin x, y = 2∙sin x and
y = ½∙sin x
y = ½∙sin x
The graphs are as follows:

As might have been expected the amplitude of the wave doubles when we multiply 2. The amplitude is the maximum height of the wave above the line of symmetry (in this case the x – axis). If we multiply by a number less than one the amplitude is less than that of the original sine wave.
If we multiply by a negative number the wave is reflected in the x – axis (turns upside down).
Example 6
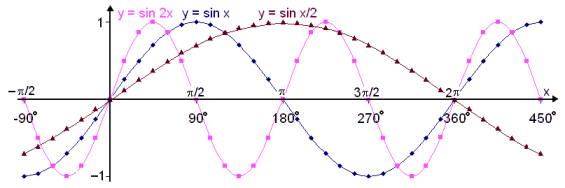
Now let’s see what effect multiplying x by a constant number has on the graphs. We’ll compare the graphs of y = sin x, y = sin 2x and y = sin x/2.

We see that multiplying x by a constant affects how often the wave repeats itself. In other words it affects the period or wave length of the graph.
The basic Sine function has a period or wave length of 2 , or 360°. This means that it repeats itself at 2
, or 360°. This means that it repeats itself at 2 intervals. This is the length on the x axis from the start of one wave to the start of the next.
intervals. This is the length on the x axis from the start of one wave to the start of the next.
The period of the function f(x) = sin 2x is half of the period of the original function, that is  . Or we can say the number of waves over a given interval on the x axis has doubled.
. Or we can say the number of waves over a given interval on the x axis has doubled.
The period of the function f(x) = sin x/2 is double the period of the original function, that is 4 . This time the number of waves over a given interval has decreased by half.
. This time the number of waves over a given interval has decreased by half.
In general we can show that if x is multiplied by the constant b then the period of the wave will be 2 /b.
/b.
Here is a summary of the results found in the above examples.
| Given the function f(x) = c∙sin b∙(x − a) + e
a is the translation of the wave to the right if a is positive, to the left if a is negative.
The period or wave length is 2
c is the amplitude of the wave.
e is the vertical translation of the wave. Up if e > 0, down if e < 0.
|
Example 7
Look at the function f(x) = 3∙sin 2(x −a = p/4, which means that the wave has been translated by
e = 3 so the wave has been translated 3 units vertically up.
b = 2 so the period is 2
c = 3 so the amplitude of the wave is 3.
Now we’ll use this information to draw the graph.

Example 8
Draw the graph of f(x) = tan x.
We know that tan x = sin x/cos x so it doesn’t exist when cos x = 0. This means that vertical asymptotes occur whenever cos x = 0, that is when x = 

The tangent function is always increasing ( goes up as we move to the right ).
It is steep near to the asymptote in x = −
The function takes the value −1 when x = −
x = 0. It then takes the value 1 in x =
Try Quiz 3 on Trig functions.
Remember to use the checklist to keep track of your work.










No comments:
Post a Comment