广义相对论课件第八章_百度文库
wenku.baidu.com/view/188e5e7f5acfa1c7aa00ccc5.html
轉為繁體網頁
0 空间是弯曲的，黎曼几何负曲率空间的总体积是无限的； 正曲率空间的总体积是
wenku.baidu.com/view/188e5e7f5acfa1c7aa00ccc5.html
轉為繁體網頁
轉為繁體網頁
广义相对论课件第八章_百度文库
wenku.baidu.com/view/188e5e7f5acfa1c7aa00ccc5.html
轉為繁體網頁
轉為繁體網頁
神秘现象全记录: - Google 圖書結果
books.google.com.hk/books?id=wkViAgAAQBAJ - 轉為繁體網頁
2013
这个“无穷大”奇点,温度无限高、密度无限大、时空曲率也无限大(三维空间曲率为零) ... 广义相对论的研究表明,宇宙中的物质存在一个临界密度ρc,大约是每立方米三个 ...科学网—物理学中的几率与曲率- 吴新忠的博文
blog.sciencenet.cn/blog-1668877-821814.html
轉為繁體網頁
轉為繁體網頁
http://www.cchere.com/article/3674028
24.1 时空没有自然的分解，但时空可被分解
广义相对论中的时空是没有自然的分解为时间与空间的办法的（其实在狭义相对论中也是这样）。但没有自然的分解不代表不能分解。事实上每个观察者都可以选择自己的时空分解。然而我们讲过 单个观察者使用的时空分解只是局部的。
能不能有整体的时空分解呢？我们考虑以下的可能性：能否存在一个整体的坐标时间 以使得时空是一个三维的流形沿着1维的坐标时间线移动而扫出来的，即 对每一个坐标时刻，时空在这一时刻的截面都是 相同的3维流形（注意我没说是相同的度量流形）
。整体的意思是 我们把三维的流形上的每一个点都看作一个观察者的话， 这些观察者都使用相同的坐标时间。注意我说坐标时间线 就已经意味着 对每个上述的观察者而言 沿着整体坐标时间运动的世界线都是类时的。如果有一个 这样的整体的坐标时间 我们就有无穷多的其他的 整体的坐标时间。这是因为我们可以把观察者们的世界线 作连续的形变（只要形变幅度不大 就仍然是类时的）。从这个意义上讲 没有一个自然的优于其他的 整体坐标时间的选择。
相对论与黎曼几何-3-曲面的微分几何
精选
||
3. 曲面的微分几何
用微积分的方法对曲线及曲面进行研究，除了欧拉、克莱洛等人的贡献之外，蒙日（GaspardMonge，1746-1818）的工作举足轻重。蒙日是画法几何学的创始人，他也对曲线和曲面在三维空间中的相关性质作了详细研究，并于1805年出版了第一本系统的微分几何教材：《分析法在几何中的应用》。这部教材被数学界用达40年之久，蒙日自己培养了一批优秀的数学人才，其中包括刘维尔、傅立叶、柯西等人，形成所谓“蒙日微分几何学派”。他们的特点是将微分几何与微分方程的研究紧密结合起来，因而，在研究曲线和曲面微分几何的同时，也大大促进了微分方程，特别是偏微分方程理论的进展。
上一节中叙述了空间曲线的曲率和挠率。曲率和挠率在空间的变化规律完全决定了这条空间曲线。三维空间的曲面又有哪些我们感兴趣的基本性质呢？我们生活的世界就是一个三维空间，人们对三维以下空间中的现象应该是很熟悉的，即使没有受过很多数学专门训练的人，也不难理解三维空间中曲线和曲面的概念。如何得到一条曲线？很简单，用笔尖在纸上一画就有了，那是平面曲线。得到空间曲线也不难，用笔尖在空间中“一画”，就能得到一条任意的空间曲线。比如说，想象一个小蚂蚁在泥土中钻来钻去，它走的路线就是一条空间曲线。换言之，空间曲线能够用一个点在空间移动而得到。那么，我们再想象一下，如果不是一个点，而是将一条曲线在空间移动的话，就应该得到一个嵌在三维空间的曲面了。
如果不考虑任意曲线的移动，而只是将我们的想象限制在比较简单的情况：我们用一把“尺”（直线的一段），将它在空间中移动，这样也能得到空间中的一个曲面。数学家们将这种由于“尺子”的移动，或者说，由于“一条直线”的平滑移动，而产生的曲面，叫做“直纹面”。法国数学家蒙日对直纹面进行了许多研究。
如图2-3-1a所示，想象一根尺子的两端A和B分别沿着曲线C1和C2移动，形成一个直纹面。
图2-3-1：各种直纹面
一把尺子在空间移动的方式可以多种多样，这样就形成了各种不同的直纹面，见图2-3-1。
最简单的情形就是这把尺子在空中平行地移动，即尺子两端按照同样的规律移动，比如说，当尺子移动的轨迹也是一条直线的话，那就将形成一个平面。稍微复杂一点，如果尺子移动的轨迹是一条任意曲线，就将形成一个如图2-3-1b所示的柱面。又如图（c）显示的情形：尺子下端移动，但上端固定不动，这时则会形成一个锥面。在图（d）中，尺子的A端沿着曲线C1，并且尺子的方向总是保持与C1相切，如此而成的曲面叫做切线面。此外，还有很多别的形状的直纹面，如图2-3-1中所画出的双曲面、螺旋面、马鞍面等等。
柱面、锥面、和切线面这三种直纹面具有一个共同的特性：它们可以被展开成平面。将一个圆柱形的纸筒沿轴向剪开，或者将一个锥形剪开到顶点，都可以将剪开后得到的图形平摊在桌面上而没有任何皱褶，这样的曲面叫做“可展曲面”。切线面也是一种可展曲面，但是，双曲面、螺旋面、马鞍面等都不是可展曲面。
数学上可以证明，可展曲面只有刚才提到的三种直纹面。也就是说，可展曲面都是直纹面，但直纹面却不一定可展，比如图2-3-1的双曲面、螺旋面、马鞍面等就是不可展曲面的例子。
球面不是直纹面，球面也是不可展的。一顶做成近似半个球面的帽子，无论如何你怎么剪裁它，都无法将它摊成一个平面，这是我们日常生活中熟知的常识。
一个曲面到底是可展还是不可展？这点对物理学家来说很重要，比一个曲面是否直纹面要重要得多。那么，我们需要知道的是：是什么几何量决定了曲面的可展性？
前面在讨论空间曲线时提到过，曲率和挠率这两个几何量，决定了曲线在三维空间中某一点的形态。曲线与曲面的情况有所不同，所有的曲线都是可展的。一根绳子，无论弯曲成什么形状，都可以把它展开伸长成一条直线。然而，我们可以将曲线研究中定义的曲率概念使用到曲面的微分几何研究中。
通过曲面上的一个给定点G，可以画出无限多条曲面上的曲线，因而可以作无限多条切线。可以证明，这些切线都在同一个平面上，这个平面被称为曲面在这点的切平面，通过该点与切平面垂直的直线叫做曲面在这点的法线。
现在，我们通过法线可以作出无限多个平面，这每一个平面都与曲面相交于一条平面曲线C，并且，可以定义平面曲线C在G点的曲率，如图2-3-2a所示，曲线C1、C2……在G点的曲率分别为Q1、Q2……。
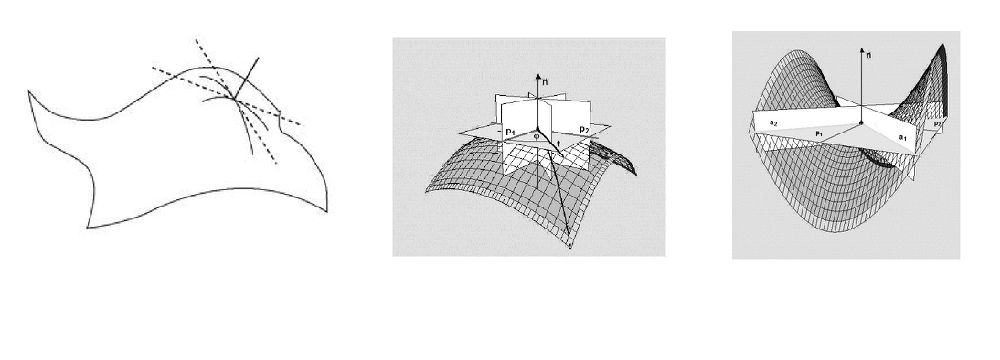
图2-3-2：曲面的两个主曲率
在所有的这些曲率（Q1、Q2……）中，找出最大值和最小值，把它们叫做曲面在点G的主曲率。对应于两个主曲率的切线方向（或两个法平面方向）总是互相垂直的。这是大数学家欧拉在1760年得到的一个结论，称之为曲面的两个主方向。从图2-3-2b和图2-3-2c可以看到，两个主曲率可正可负。当曲线转向与平面给定法向量相同方向时，曲率取正值，否则取负值。
让我们再重复并加深一点对可展性的理解。首先，对曲线而言，任意一条空间曲线，都是可展的，都可以伸展为一条直线。不同的空间曲线只是由它们“嵌入3维空间中时”的弯曲和扭曲程度而区分，如果只从曲线上看，所有的曲线都是一样的，都与直线具有同样的几何性质。换言之，如果有一种极小的蚂蚁生活在一条空间曲线上，它在曲线上不能知道周围空间的任何信息，那么，它感觉不出它的曲线世界与其它的曲线（或直线）有任何的不同。
曲面则有可展（成平面）与不可展之分。一个球面是不可展的，因为你不可能将它铺成一个平面，而柱面可展，它具有与平面完全相同的内在几何性质。如果有一种生活在柱面上的生物的话，它会觉得与生活在平面上是一模一样的，但球面生物就能感觉到几何上的差异。比如说，柱面生物在它的柱面世界中画一个三角形，将三角形的三个角加起来，会等于180度，这个结论与平面生物得到的一致。而球面生物在它的世界中画一个三角形，它将会发现三角形的三个角加起来，要大于180度。
这种与曲面嵌入3维空间的弯曲方式无关，只研究所谓曲面本身上的几何，叫做内蕴几何。
高斯是研究内蕴几何之第一人。他在1827年发表了《关于曲面的一般研究》，研究曲面情形之下能够发展的几何性质。他最初的目的是为了应用，因为当时的德国Hannover 政府要他主持一个测量工作，为了给这个测量工作一个理论甚础，于是高斯写下了这篇当时在微分几何上最重要的论文，抓住了微分几何中最重要的概念，建立了曲面的内在几何，奠定了近代形式曲面论的基础，使微分几何自此成了一门独立的学科。
什么样的几何量才能够代表曲面的内蕴几何性质呢？
几何直观地介绍广义相对论中的时空以及大爆炸模型 （14） [ changshou ] 于:2012-02-14 19:21:30 复:3659016
几何直观地介绍广义相对论中的时空以及大爆炸模型 （14） [ changshou ] 于:2012-02-14 19:21:30 复:3659016
几何直观地介绍广义相对论中的时空以及大爆炸模型 （14）因果结构
提示：这篇不理解的话，可以跳过。
14.1 狭义相对论中的因果结构
狭义相对论中如果一个观察者超光速会怎样? 超光速意味着世界线落在光锥外， 即 世界线可以把 两个类空间隔的点联系起来。于是这两个点处发生的事情可以有物理联系。 比如 第二个点处发生的事（结果） 可以是由第一个点处发生的事（原因）引起的。可是用洛仑兹变换不难证明 存在惯性参照系 使得在这惯性参照系看来 第二个点处发生的事（结果）发生在前， 第一个点处发生的事（原因）发生在后。于是在这惯性参照系看来 因果关系被破坏了。如果不想因果关系被破坏， 我们就得禁止超光速运动。也就是说观察者的世界线应该是 类时世界线（亚光速运动）。
14.2 广义相对论中的观察者的世界线应该是 类时世界线
这是14.1 和13.3 的结合。
14.3 时间定向的洛仑兹流形
闵可夫斯基时空是有时间定向的。 我们可以分过去未来。这意味着我们需要 给每一条世界线定方向
。取某个点A上的光锥。它由两个锥形分支尖对尖的组成（两个锥形分支的尖点都是点A）。 为啥是两个？ 因为光锥 是由 坐标平方 三正一负的加起来等于0 这个条件定义的。如果一个点在光锥上，把它的坐标全添上负号得到一个新的点。 新的点的坐标平方没变，三正一负的加起来仍等于0， 所以仍在光锥上。这个对称性说明光锥有两个形状相同的分支对称的放置在一起。一个分支里的时间坐标是负号，另一个是正号。所以一个对应光在过去（点A的过去）的轨迹，另一个对应光在未来（点A的未来）的轨迹。 这两个分支一个称为过去光锥 一个称为未来光锥。这两部分的内部各自对应 过去与未来的 与点A类时间隔的点。 所以 对一条类时世界线（观察者的世界线） 我们知道 它在某点的未来方向 是指向该点的未来光锥内部的。 由于光锥被洛仑兹变换保持， 不同惯性参考系对时间方向不会有不同看法。
我们要求洛仑兹流形也有类似的用光锥定义的时间定向。细节不重要。大致说来，有的洛仑兹流形可以，有的不可以。所以我们应该要求，时空是 可以时间定向的洛仑兹流形。 以后我要举的例子 都是这样的。但要注意的是 洛仑兹流形上用光锥场（见13.3）来定义时间方向只能是局部的。
14.4 广义相对论中的因果结构
乍看起来14.2 保证了广义相对论中 因果关系也不被破坏。但还有其他可以破坏因果关系的机制。比如 由于洛仑兹流形整体上 可以不是闵可夫斯基时空， 我们不能排除 某个观察者的世界线（类时世界线）首尾相接的可能。 这意味着 沿着这观察者的世界线走 在任何一点 都有良好的时间定向， 但整体上 他却回到了他时空之旅的起点（注意这意味着他回到了过去的某个时刻）
。这里的破坏机制 是我们有局部的时间定向，但没有整体的 （因为有首尾相接的类时世界线）。这与闵可夫斯基时空中超光速破坏因果关系的机制 完全不同。更糟糕的是有些这类例子 满足爱因斯坦方程 属于“可能的时空”（见（16）篇）
。
物理学家倾向于 以违反因果关系为由 排除这类时空。 为了解决 广义相对论中的可能的因果矛盾，一个一劳永逸的办法是规定 我们考虑的时空 作为一个流形 应该是由 一个3维的切片 沿着一条1维的不闭合的线运动而扫出来的。 这条1维的线 应该代表 某个观察者的世界线， 所以应该是类时曲线。3维的切片 对这个观察者而言， 就是时空的空间部分。
我们以后谈时空分解和演化时 还会再回来谈因果结构。
待续
提示：这篇不理解的话，可以跳过。
14.1 狭义相对论中的因果结构
狭义相对论中如果一个观察者超光速会怎样? 超光速意味着世界线落在光锥外， 即 世界线可以把 两个类空间隔的点联系起来。于是这两个点处发生的事情可以有物理联系。 比如 第二个点处发生的事（结果） 可以是由第一个点处发生的事（原因）引起的。可是用洛仑兹变换不难证明 存在惯性参照系 使得在这惯性参照系看来 第二个点处发生的事（结果）发生在前， 第一个点处发生的事（原因）发生在后。于是在这惯性参照系看来 因果关系被破坏了。如果不想因果关系被破坏， 我们就得禁止超光速运动。也就是说观察者的世界线应该是 类时世界线（亚光速运动）。
14.2 广义相对论中的观察者的世界线应该是 类时世界线
这是14.1 和13.3 的结合。
14.3 时间定向的洛仑兹流形
闵可夫斯基时空是有时间定向的。 我们可以分过去未来。这意味着我们需要 给每一条世界线定方向
。取某个点A上的光锥。它由两个锥形分支尖对尖的组成（两个锥形分支的尖点都是点A）。 为啥是两个？ 因为光锥 是由 坐标平方 三正一负的加起来等于0 这个条件定义的。如果一个点在光锥上，把它的坐标全添上负号得到一个新的点。 新的点的坐标平方没变，三正一负的加起来仍等于0， 所以仍在光锥上。这个对称性说明光锥有两个形状相同的分支对称的放置在一起。一个分支里的时间坐标是负号，另一个是正号。所以一个对应光在过去（点A的过去）的轨迹，另一个对应光在未来（点A的未来）的轨迹。 这两个分支一个称为过去光锥 一个称为未来光锥。这两部分的内部各自对应 过去与未来的 与点A类时间隔的点。 所以 对一条类时世界线（观察者的世界线） 我们知道 它在某点的未来方向 是指向该点的未来光锥内部的。 由于光锥被洛仑兹变换保持， 不同惯性参考系对时间方向不会有不同看法。我们要求洛仑兹流形也有类似的用光锥定义的时间定向。细节不重要。大致说来，有的洛仑兹流形可以，有的不可以。所以我们应该要求，时空是 可以时间定向的洛仑兹流形。 以后我要举的例子 都是这样的。但要注意的是 洛仑兹流形上用光锥场（见13.3）来定义时间方向只能是局部的。
14.4 广义相对论中的因果结构
乍看起来14.2 保证了广义相对论中 因果关系也不被破坏。但还有其他可以破坏因果关系的机制。比如 由于洛仑兹流形整体上 可以不是闵可夫斯基时空， 我们不能排除 某个观察者的世界线（类时世界线）首尾相接的可能。 这意味着 沿着这观察者的世界线走 在任何一点 都有良好的时间定向， 但整体上 他却回到了他时空之旅的起点（注意这意味着他回到了过去的某个时刻）
。这里的破坏机制 是我们有局部的时间定向，但没有整体的 （因为有首尾相接的类时世界线）。这与闵可夫斯基时空中超光速破坏因果关系的机制 完全不同。更糟糕的是有些这类例子 满足爱因斯坦方程 属于“可能的时空”（见（16）篇）。物理学家倾向于 以违反因果关系为由 排除这类时空。 为了解决 广义相对论中的可能的因果矛盾，一个一劳永逸的办法是规定 我们考虑的时空 作为一个流形 应该是由 一个3维的切片 沿着一条1维的不闭合的线运动而扫出来的。 这条1维的线 应该代表 某个观察者的世界线， 所以应该是类时曲线。3维的切片 对这个观察者而言， 就是时空的空间部分。
我们以后谈时空分解和演化时 还会再回来谈因果结构。
待续
No comments:
Post a Comment