在讨论地球潮汐成因时,地球绕太阳运行轨道与月球绕地球运行轨道可视为圆轨道。已知太阳质量约为月球质量的2.7e7倍,地球绕太阳运行的轨道半径约为月球绕地球运行的轨道半径的400倍。关于太阳和月球对地球上相同质量海水的引力,以下说法正确的是:
如图,地球半径远小于日地距离。计算地表某处太阳引力场,可以以(r/R)展开,领头是平方反比引力场。但是地球在绕太阳转动,在地球上看来,领头项可以被惯性力精确抵消,剩余部分领头项就是正比于R^(-3)的项了。
2. 牛顿引力
当年,18岁的克莱洛因为对空间曲线曲率和挠率的研究而被选入了法国科学院,在那儿,他与皮埃尔·莫佩尔蒂成为了好朋友。莫佩尔蒂比克莱洛大15岁,但在当时也算是一名相当年轻的科学院院士。莫佩尔蒂后来因为研究最小作用量原理而知名,我们曾经在第一篇中提到过他在这方面的贡献。那个时代,欧洲的数学界和物理界,小天才颇多,年轻学子意气风发、英雄辈出。比克莱洛大五岁的欧拉以及比克莱洛小五岁的达朗贝尔,都是在12、3岁的小小年纪就进了大学。之后,这三个人在研究牛顿引力定律的过程中还演绎了一些值得回味的故事。
引力是一种颇为神秘的作用力,它存在于任何具有质量的两个物体之间。人类应该很早就认识到地球对他们自身以及他们周围一切物体的吸引作用,但是,能够发现“任何”两个物体之间,都具有万有引力,就不是那么容易了。其原因是因为两个普通物体之间的引力是非常地微弱,使得我们根本不能感知它们的存在。比较起来,电磁力就要大多了,比如我们司空见惯的摩擦生电的现象:一个绝缘玻璃棒被稍微摩擦几下,就能够吸引一些轻小的物品;还有磁铁对铁质物质的吸引和排斥作用,都是很容易观察到的现象。然而,除了巨大质量的星体产生的引力能够被观测到之外,一般物体的引力是很难被探测到的。此外,人类对引力的本质仍然知之甚少,电磁场有电磁波来传递信息,常见的光也是一种电磁波,人类可以产生、接受、控制光波和电磁波,它们已经算是某种抓得住、看得见、用得上的东西。可是引力呢,至今仍未直接探测到引力波,我们对引力的了解还差得太远。
牛顿发现的万有引力定律是理解引力的第一个里程碑。里程碑可不是那么容易就被建在某人的名字前面的,其中伴随着许多优先权之争,特别是在科学草创、规范不健全的时代。牛顿能够和常人一样地感觉苹果打到头上,却也和常人一样地无法探测一般物体之间的引力。但他凭着他超强的思维能力以及基于前人成果的基础上,提出了万有引力定律。定律说的是任意两个物体之间都存在相互吸引力,力的大小与它们的质量乘积成正比,与它们距离的平方成反比。而其间的比例系数被称之为引力常数G。这个常数应该是个很小的数值,但到底等于多大,当时的牛顿自己也搞不清楚,一直到牛顿死后70年左右,才被英国物理学家亨利·卡文迪什(1731-1810)用一个很巧妙的扭秤方法测量出来。现在公认的万有引力常数大约为G=6.67x10-11 N·m2/kg2。从这个数值可以估计出两个50公斤成人之间距离1米时的万有引力大小只有十万分之一克!这就是为什么我们感觉不到互相之间具有万有引力的原因。
当时牛顿还研究了地球的形状,并从理论上推测地球不是一个很圆的球形,而是一个赤道处略为隆起,两极略为扁平的椭球体。由于地球的自转,地球上的所有物质都以地轴为中心做圆周运动,因而都产生惯性离心力。如图2-2-1a所示,离心力可分解为两个分力,一是垂直于地球表面的力,一是水平分力,垂直分力不会使物质沿地表移动,而水平分力不一样。地球上所有质点,无论是位于北半球还是南半球,所受的水平分力都指向赤道那一边。因此地球上的物质便会有一种向赤道挤压的趋势,使地球变成一个扁球体之后而平衡。对于这个结论,当时的学界有两派意见。莫佩尔蒂支持牛顿扁球体的结论;卡西尼等则根据其它一些理论,认为地球是个长椭球。为了解决对此问题的争论,莫佩尔蒂带领克莱洛等人以法国科学院测量队的名义进行了1年多的远征,对地球进行弧度测量,远征的测量结果证实地球确实为一扁形椭球体,赤道半径要比极半径长出20多公里。
图2-2-1:地球自转对地球形状的影响
克莱洛从1745年开始研究太阳、地球、月亮的三体问题。将牛顿定律用于解决二体问题不难,但三体问题就变得异常地复杂,之后经过庞加莱的研究还知道这个问题实际上与复杂的混沌现象有关。克莱洛当时特别计算了月球的轨道,远地点和近地点等。有趣的是,他的计算导致的第一个结论是认为牛顿重力理论的平方反比定律是错误的,而且还得到了不少同行的支持,其中包括大数学家欧拉。
欧拉当时将近40,右眼失明,却已经成为数学界的大师级人物。同时,比克莱洛小几岁、同为法国人的达朗贝尔也向法国科学院提交了一份文件,宣布与克莱洛的结果一致。于是,克莱洛信心倍增,振振有词地建议在万有引力的平方反比定律后面,再加上与半径4次方成反比的一项作为修正。
然而,到了1748年的春天,克莱洛意识到,月球远地点的观察数据与理论计算之间的差异是来自于自己计算时所作的某些不太恰当的近似【1】。于是,克莱洛在1749年宣布,他现在的理论计算结果是与平方反比定律相符合的。然而,克莱洛没有对此给出详细的解释,反而采取缄口不言的策略,默默笑观欧拉和达朗贝尔两个人为此问题而纠结却又不知如何重复克莱洛的计算。
欧拉最后想出一招,利用他在圣彼得堡学院的位置和威望,设立了一个征奖项目,要求在1752年之前精确计算出月球的远地点。克莱洛果然上钩,他提交的答案使欧拉完全理解了克莱洛的方法。
尽管欧拉为自己没有解决这个问题略感沮丧,但他高度赞赏了克莱洛的工作。
两个年轻之辈就不一样了。原本还算友好的克莱洛和达朗贝尔从此结下梁子,后来关系逐渐恶化,继而互相攻击,情势愈演愈烈。两个人本来都是数学家,但达朗贝尔更为重视理论方面,克莱洛便以此攻击达朗贝尔等理论家忽视实验,采用不靠谱的假设和分析方法来避免实验和繁琐的计算。反之,达朗贝尔则嘲笑克莱洛对三体问题的结果都是基于别人的观察资料而非像他那样,是基于自己的理论而得到的。
我们如今很难用是非的标准来判定两人的争论。历史地看,重理论的达朗贝尔后来的名声更大一些,但在当年,克莱洛却是份外的风光。因为他继续使用自己计算三体问题的技巧,精确地预测了哈雷彗星的轨道。他在1758年11月14号宣布结果,预测哈雷彗星将于1759年4月15日返回地球,后来,哈雷彗星于1759年3月13日返回了地球,与预测日期只相差一个月,这是由于当时还未被发现的天王星和海王星对哈雷彗星的摄动影响没有被考虑进去的原因,使克莱洛的预言产生了小小的误差。这个预言再次证实了牛顿引力理论的正确,克莱洛也因此而获得了公众的极大好评。
克莱洛后来在社会中声名大振,却反而阻碍了他的科学研究工作,他日夜奔波于社交场合,四处赴宴熬夜,身边常有女人陪伴。他因此而失去了休息和健康,在52岁时英年早逝。
如上所述,克莱洛、欧拉等当初都怀疑过万有引力遵循的平方反比律,其实现在看起来,这平方反比律是大有来头的。静电力和引力相仿,也遵循平方反比律,还有其它一些现象,诸如光线、辐射、声音的传播等,也由平方反比规律决定。为什么刚好是平方反比、是2而非其它呢?大自然似乎总是以一种高明而又简略的方式来设置自然规律,在这儿它又是如何呈现它的高明之处的?时间的积累以及科学家们的努力,部分回答了这个问题。人们逐渐认识到,这个平方反比率不是随便任意选定的,它和我们生活在其中的空间维数为3有关。
图2-2-2:点信号源的传播服从平方反比律
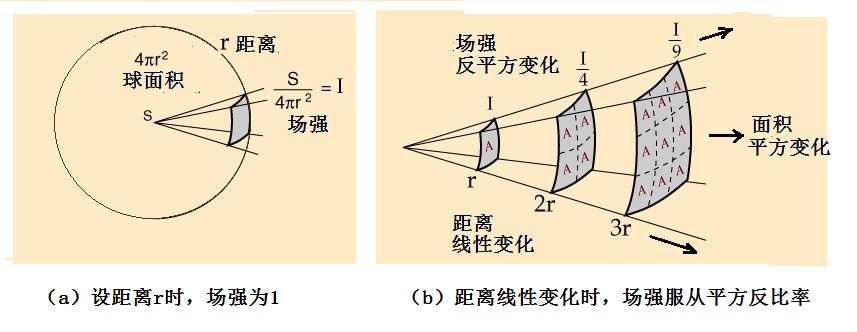
在各向同性的3维空间中的任何一种点信号源,其传播都将服从平方反比定律。这是由空间的几何性质决定的。设想在我们生活的3维欧几里德空间中,有某种球对称的(或者是点)辐射源。如图2-2-2所示,其辐射可以用从点S发出的射线表示。一个点源在一定的时间间隔内所发射出的能量S是一定的。这份能量S向各个方向传播,不同时间到达不同大小的球面。当距离r呈线性增加时,球面面积4pr2却是以平方规律增长。因此,同样一份能量,所需要分配到的面积越来越大。比如说,假设距离为r时,场强I=S/(4pr2),将这个数值用1来表示的话,当距离变成2r的时候,同样的能量需要覆盖原来4倍的面积,因而使强度变成了1/4,下降到原来的四分之一。这个结论也就是场强的平方反比定律。
从现代的矢量分析及场论的观点,可以对平方反比律解释得更深入一些。简略地说,服从平方反比律的场有一些“优美”的特点:是“无旋”的、是保守力场、是有心力场、无源处的场的散度为0、场强可以表示为某个标量的梯度、做功与路径无关等等。从场论的观点,在n维欧氏空间中,场强的变化与r(n-1)成反比,当n=3,便化简到了平方反比定律。
追溯万有引力的平方反比定律的发现历史,便扯出了牛顿与胡克间的著名公案。其实胡克对万有引力的发现及物理学的其它方面都做出了不朽的贡献,但现在的一般人除了有可能还记得中学物理中曾经学过一个“胡克定律”之外,恐怕就说不清楚这胡克是谁了。这都无可奈何,成者为王败者寇,学术界也基本如此。对此公案大家可能都有所闻,本人不再赘述,可阅读参考文献【2】。

No comments:
Post a Comment