法蘭克的數學世界
在此我想回答一些網友(非數學專業的)關於微分算子與微分方程的一些概念。微分方程的問題開始主要是來自於自然哲學(物理學),不管是常微分方程,或是偏微分方程。
假設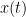 表直點的位置與時間的關係,令
表直點的位置與時間的關係,令 表速度與位置的關係,那麼一次以下的常微分方程
表速度與位置的關係,那麼一次以下的常微分方程
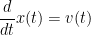 ,
,  。
。
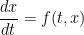 ,
, 。
(
。
( 可以是向量值,可以是純量)。而
可以是向量值,可以是純量)。而 是一個實值或向量值的函數(real-valued or vector valued functions)。我們必須思考,這樣的問題是否真的可以解?如果解本身是不存在的,那麼何來去解他呢?但,事實上,在微分方程的歷史中,剛開始數學家都是一股腦兒的用很多特殊的技巧去解方程,而非先證明解的存在性。然而,能夠用一些初等技巧解決的方程是少之又少。於是,數學家陷入了瓶頸。
是一個實值或向量值的函數(real-valued or vector valued functions)。我們必須思考,這樣的問題是否真的可以解?如果解本身是不存在的,那麼何來去解他呢?但,事實上,在微分方程的歷史中,剛開始數學家都是一股腦兒的用很多特殊的技巧去解方程,而非先證明解的存在性。然而,能夠用一些初等技巧解決的方程是少之又少。於是,數學家陷入了瓶頸。
在方程的歷史中,有一樣驚人的的創作,是出自於富利葉(Fourier)之手的,利用三角級數解決熱傳導的問題。當然,在那之前,數學家也思考用解析(冪級數)的方式去解微分方程的問題。Fourier的做法以現今數學觀點來看是相當不嚴謹的。然而,我們也不得不佩服他的獨創性。另外一個著名的工作就是出自於Volterra。Volterra利用方程的方法去研究生物生態學,(是他的一位好友讓他去研究義大利附近的海域魚群的生態)。接下來,微分方程漸漸地以一種專門的研究出現在數學的領域中。在那之前,數學家並不會專門的去研究方程,而是在致力於解決某一類的問題,如來自物理學的,來自於化學的,或是來自於幾何學等等的。
後來,Fredeholm研究積分方程提供了線性代數的方法解決積分方程的問題。這讓微分方程有了另外一種觀點(似乎並不是新的觀點)。當然在那同時期,恰巧是量子物理學正大肆橫掃古典物理的革命時期。積分方程,微分方程,到了Hilbert的手中,漸漸的融合成現今的泛函分析的起源。而解決微分方程,就用了線性代數的觀點,就是算子的概念。回到我們之前的問題。
首先我們必須考慮的是:我們想研究的函數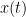 是屬於麼樣的函數?連續?可微?時間的區間?解是否存在?如果我們把微分的過程視為由一個空間至另外一個空間的映射,那麼這樣的空間是屬於哪樣的空間呢?所有的可微分函數?連續的可微分函數?我們當然可以很簡單的說
是屬於麼樣的函數?連續?可微?時間的區間?解是否存在?如果我們把微分的過程視為由一個空間至另外一個空間的映射,那麼這樣的空間是屬於哪樣的空間呢?所有的可微分函數?連續的可微分函數?我們當然可以很簡單的說 是微分算子
是微分算子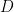 的preimage,但是,那必須在一個前提之下,
的preimage,但是,那必須在一個前提之下,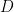 所定義的空間被決定。當然
所定義的空間被決定。當然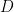 所定義的空間仰賴於我們所希望研究的空間。(註:利用泛函分析的方法並不是唯一研究方程的方法,而是他提供了一套有系統的研究方法)。因為,並不是任何的空間對我們來說都是有意義的。這也是為何會利用到Hilbert空間,或是Banach空間的理由。因為在量子物理中,粒子所存在的空間就是Hilbert空間
所定義的空間仰賴於我們所希望研究的空間。(註:利用泛函分析的方法並不是唯一研究方程的方法,而是他提供了一套有系統的研究方法)。因為,並不是任何的空間對我們來說都是有意義的。這也是為何會利用到Hilbert空間,或是Banach空間的理由。因為在量子物理中,粒子所存在的空間就是Hilbert空間 ,或是
,或是![L^2[a,b] L^2[a,b]](http://s0.wp.com/latex.php?latex=L%5E2%5Ba%2Cb%5D&bg=FFFFFF&fg=000000&s=0) 。而微分算子所定義的空間就是所謂的Sobolev空間。
。而微分算子所定義的空間就是所謂的Sobolev空間。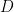 的意義就給的更清楚了。然而在解方程的過程中,如給定
的意義就給的更清楚了。然而在解方程的過程中,如給定 是連續函數
是連續函數
 ,
,  。
那麼微分算子(泛函分析)並不是一個簡單的方式去解決這樣的問題,而且是更加的複雜。(對某些問題來說),而一般工程數學上所謂的
。
那麼微分算子(泛函分析)並不是一個簡單的方式去解決這樣的問題,而且是更加的複雜。(對某些問題來說),而一般工程數學上所謂的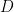 指的並不是微分算子,所謂的符號數學(Symbolic math)。利用某些觀念,或是符號可以幫助我們去解決問題,就如同前面有網友說的heaviside function或是Dirac function。其實在數學裡面,他的背景就是Distribution theory。而這正是Schwartz拿fields medal的得意之作。他們並不是不嚴謹,而是他們的背景並不是很容易,如果避掉了這些理論,用符號運算去解決方程,的確是一個方便的工具。
指的並不是微分算子,所謂的符號數學(Symbolic math)。利用某些觀念,或是符號可以幫助我們去解決問題,就如同前面有網友說的heaviside function或是Dirac function。其實在數學裡面,他的背景就是Distribution theory。而這正是Schwartz拿fields medal的得意之作。他們並不是不嚴謹,而是他們的背景並不是很容易,如果避掉了這些理論,用符號運算去解決方程,的確是一個方便的工具。
Kx 2 && + ω0 x = 0 x dx & x= dt 线性常系数齐次常微分方程圆频率(角频率) 惯性和弹性2011-1-29 K ω = m 2 0 1 f0 = 2π 理论声学(1) 第一章K 1 = m 2π 1 mCm 3 定 ...
2010年12月8日 - Kx 2 && + ω0 x = 0 x dx & x= dt 常微分方程圆频率(角频率) 惯性和弹性2010-12-8 K ω = m 2 0 1 f0 = 2π 理论声学(1) 第一章K 1 = m 2π 1 mCm 3 ...
在运动方程中位移的一阶导数项与衰减对应。 2011-1-29 理论声学(1) 第一章29 相平面(空间) 相平面? 系统状态由位移和速度确定& ? 用( x, x ) 平面的点表示?
第01章简单振子的振动 · 第02章质点系的振动 ... 有限空间的传播? 管道的传声问题 ..... 2 a 对时间和空间平均后2013-7-11 理论声学(2) 第八章? ? 1 4 ?0c 2 47 波印 ...
微分方程與微分算子
時間: Tue Jul 17 16:36:44 2007
本篇作於pttMath版
目的:希望提供一些學生微分方程方面的看法。
本文:本篇作於pttMath版
目的:希望提供一些學生微分方程方面的看法。
在此我想回答一些網友(非數學專業的)關於微分算子與微分方程的一些概念。微分方程的問題開始主要是來自於自然哲學(物理學),不管是常微分方程,或是偏微分方程。
假設
描述了物體的運動現象。隨著各類科學的發展,微分方程的內容也變得更多樣性了。從簡單的一次線性微分方程,發展到了高階非線性微分方程,通常我們可以用以下的微分方程來描述所有的常微分方程:
在方程的歷史中,有一樣驚人的的創作,是出自於富利葉(Fourier)之手的,利用三角級數解決熱傳導的問題。當然,在那之前,數學家也思考用解析(冪級數)的方式去解微分方程的問題。Fourier的做法以現今數學觀點來看是相當不嚴謹的。然而,我們也不得不佩服他的獨創性。另外一個著名的工作就是出自於Volterra。Volterra利用方程的方法去研究生物生態學,(是他的一位好友讓他去研究義大利附近的海域魚群的生態)。接下來,微分方程漸漸地以一種專門的研究出現在數學的領域中。在那之前,數學家並不會專門的去研究方程,而是在致力於解決某一類的問題,如來自物理學的,來自於化學的,或是來自於幾何學等等的。
後來,Fredeholm研究積分方程提供了線性代數的方法解決積分方程的問題。這讓微分方程有了另外一種觀點(似乎並不是新的觀點)。當然在那同時期,恰巧是量子物理學正大肆橫掃古典物理的革命時期。積分方程,微分方程,到了Hilbert的手中,漸漸的融合成現今的泛函分析的起源。而解決微分方程,就用了線性代數的觀點,就是算子的概念。回到我們之前的問題。
首先我們必須考慮的是:我們想研究的函數
第01章简单振子的振动_百度文库
wenku.baidu.com/view/c4dee8d87f1922791688e8c2.html - 轉為繁體網頁
理论声学 - 百度文库
wenku.baidu.com/view/1a6f9dd73186bceb19e8bbae - 轉為繁體網頁
第01章简单振子的振动_百度文库
wenku.baidu.com/view/c4dee8d87f1922791688e8c2.html - 轉為繁體網頁
第08章波导_百度文库
wenku.baidu.com/view/4636b5573c1ec5da50e2703b.html
轉為繁體網頁
轉為繁體網頁
No comments:
Post a Comment