phymath999: 非对易量子场论不是一个局域场论，紫外物理影响红外行为; 單擺的週期只與擺長有關，而與擺錘的質料無關

Saturday, January 24, 2015

非对易量子场论不是一个局域场论，紫外物理影响红外行为; 單擺的週期只與擺長有關，而與擺錘的質料無關

http://power.itp.ac.cn/~mli/stringbook56.txt

由於實驗的結果是：單擺的週期只與擺長有關，而與擺錘的質料無關；所以牛頓以

\frac{m_G}{m_I}=1 + O(10^{-3})\,

的精確度於1680年接受了

m_I=m_G\,

的結論。
在牛頓之後，厄阜於1890年25年間，以鉑為基準用八種不同的材料去進行攏扭實驗，去測量引力質量與慣性質量的比例與1的偏離，從實驗的精確度，厄阜的結論是：

\frac{m_G}{m_I}=1 + O(10^{-8})\,

到了1962年，迪克改進了厄阜攏扭實驗之精確度至

10^{-11}

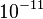；到了1971年，布拉金斯基及潘洛夫等人又將實驗之精確度推至

10^{-12}

。此外還有別的科學家用實驗測定了原子和原子核的結合能所對應的引力質量與慣性質量之比，亦沒有發現對1之偏離（雖精確度不及厄阜攏扭實驗）。因此，在目前的精確度甚高之下，可證實：

m_I=m_G\,

從兩種質量的觀念上來說，他們是本質不同的物理量；但如果兩者的值之比例對一切物體相同，在實用上可把他們當同一個量來對待（即是物體的質量），這就是引力質量與慣性質量成正比例；在適當的單位制下，即令比例常數成為1，引力質量與慣性質量相等。

第十五章结语与展望第一节李淼可以说，弦论的第二次革命是自94年场论和弦论中的强弱对偶的发现始，至98年的马德西纳猜测结束。98年之后，虽然弦论中每年或多或少还有一些新的进展，概念上的变化和进展基本上没有了。超弦的第二次革命不但带来弦论本身研究的极大变化，也影响了许多临近的领域，如数学、粒子物理唯象学以及宇宙学。在这最后一章中，我们不再提到对数学的影响，但会提及对粒子物理和宇宙学的一些影响。我们不准备另立专章介绍98年以后的一些重要进展，在本章中，我们扼要介绍一下这些发展，同时也强调第二次革命带来的一些深刻问题。与马德西纳猜测提出的同时，道格拉斯等人指出在矩阵理论中可以实现非交换几何。他们的具体例子是，将M理论紧化在一个两维环面上，同时三阶反对称张量场在这个两维环面以及纵向方向（就是矩阵理论中所有物体都带有动量的那个方向）有一个不为零的常数分量，那么矩阵理论就是一个三维的非交换超对称规范理论。这里非交换的意思不是指规范群－规范群总是非交换的，而是指定义规范理论的空间本身是非交换的。这篇文章的作者之一，A. 孔(A. Connes)，是一个有名的数学家，也是数学中非交换几何的创始人。他有一个完整的非交换几何的定义，早在1985 年威顿就将他的非交换几何概念应用到弦场论中去。而在孔等人的文章中，非交换几何以最为简单的形式出现。简单地说，三维规范理论中的那个两维空间是一个非交换环面，是海森堡两维相空间在环面上的推广。我们知道，量子力学中，坐标与其共轭动量不对易，坐标与动量的对易子是一个常数。现在，两维环面上的两个坐标的对易子也是一个常数。很容易在一个非交换环面上定义场论。在寻常环面上的经典场是环面上两个坐标的函数，现在，环面坐标不再是普通数，而是算子了，所以经典场应该是两个算子的函数。尽管是经典场，其表现形式是算子，取值范围是海森堡代数。当然，这个场还没有被量子化。我们知道，两维相空间的另外一种量子化方式是维尔的几何量子化，任何一个算子被还原成相空间上的普通函数，但两个算子的乘积不是两个普通函数的乘积，而是一种叫做星乘积的非交换乘积。普通函数的乘积是一种局域乘积，所得的函数在一点的值是原来两个函数在这一点值的乘积，而星乘积是非局域乘积，所得函数在一点的值与原来两个函数在整个空间的行为有关。利用星乘积，非交换环面上的场论就成为普通的量子场论，不同于局域量子场论的地方是作用量中的所有场的乘积是星乘积。虽然非交换场论一开始是定义在环面上的，且与矩阵理论有关，后来人们发现D膜在一个有着两阶反对称场的背景下的有效理论也是非交换规范理论。这一点可以由道格拉斯等人的工作中看出来，因为当我们将纵向方向紧化后，原来的三阶反对称场就变成弦论中的两阶反对称场。非交换量子场论也可以通过对D膜上的开弦直接量子化获得，贺培铭和朱创新在这方面作了原创工作。这个工作在99年塞伯格和威顿的长文中得到极大的广大，他们的工作也触发了弦论中新一轮的时髦。非对易几何是一个非常老的概念，许多人也一直觉得在一个量子引力理论中，经典几何应该被类似非对易几何这样的概念取代，但也一直没有具体模型。弦论中D膜在一定背景场下的理论是第一次在一个自洽的理论中实现非对易几何，由于弦论本身的自洽性，D膜上的理论是一个有定义的量子理论。如果非对易量子场论和闭弦以及开弦激发态脱耦，非对易量子场论本身就是一个完备的量子理论，特别地，这个场论是可重正的。虽然过去几年人们做了许多工作，但非对易几何却一直没有直接地在引力理论中实现。一个比较接近这样的实现是AdS/CFT对应中球面的非对易性，这些球面叫做模糊球面，模糊性的来源是引力子在反对称场的通量的影响下成为一个有限尺度的物体，其大小和位置被量子化了，与一个模糊球面的描述吻合。一个非对易场论在量子化后有一个非常有趣的性质，叫做紫外/红外混合。过去的所有的关于一个局域量子场论的经验告诉我们，量子场论在红外的性质与紫外的具体行为无关，紫外的所有影响可以被总结在几个参数中，这些参数决定红外的有效作用量。非对易量子场论不是一个局域场论，所以紫外物理影响红外行为并不令人惊讶。塞伯格等人的具体发现是，量子涨落中的高能模直接影响与这些涨落联系的低能物理过程。我们现在对这种现象有一个非常直观的理解：场在非对易场论中其实是一个偶极矩的激发，偶极矩又在一个磁场中运动（磁场这个背景场直接导致非对易性），如果偶极矩的动量越大，磁场的作用使得偶极矩的尺度越大，从而影响大尺度也就是红外物理。紫外/红外混合很像我们前面讨论过的紫外/红外对应，所以人们希望类似非对易场论的理论可以解释宇宙学常数为什么这么小。宇宙学常数决定我们的宇宙的尺度，所以是一个红外参数，如果紫外/红外混合在量子引力中是一个重要效应，那么很有可能极高能的量子引力效应导致一个非常小的宇宙学常数。可惜，这个想法还是很难用一个具体模型实现。但我们预期，弦论的下一个重要突破很可能与这个问题相关。过去几年中出现的另一个热门话题是不稳定膜和快子，这个方向几乎是森一个人独力开发的。也是在98年，当弦论界的大部分人赶热闹研究马德西纳猜测时，森开始研究弦论中的非BPS态。他从稳定的非BPS态开始，然后研究到不稳定的非BPS态，再到不稳定的BPS态如何衰变，以及衰变成稳定的BPS态。这个方向经过很多人的努力，已经派生出许多令人意想不到的应用。最有意思的是不稳定的非BPS态，这些态通常是弦论中的经典解，不带任何守恒荷，从而是不稳定的。在森研究这些物体之前，我们已经知道了一些不稳定的膜系统，一个最简单的例子是一个稳定的D膜和一个平行的反 D膜组成的系统。在D膜和反D膜之间存在吸引力，所以即使当两个对象相隔比较远时，这个系统也是不稳定的。当两个对象之间的距离很近时，班克斯和沙氏金早就指出，端点分别搭在两个膜上的开弦中出现一个不稳定模，其质量的平方是负的，就是一个快子。和传统的相对论一样，快子的出现并不意味着因果律的破坏，只是说明系统不稳定，快子本身是不稳定性的表现：当系统出现扰动时，扰动增大的部分就是快子的激发。在D膜反D膜系统中，当两个物体靠得很近时，快子被激发，快子激发的表现形式是两个物体互相湮灭。 D膜和反D膜系统可以看成是弦论树图层次上的严格解，因为可以用两维共形场论来描述这个系统。森后来指出，当我们在超弦理论中研究D膜反D膜上的开弦时，格舍奥投射与两个平行的D膜不一样，所以快子就保留了下来。虽然单独的D膜或者单独的反D膜都带有守恒荷，但整个系统的荷是零，所以守恒律不保证这个系统不湮灭。森的研究中出现一些新的不稳定系统，就是单个不稳定D膜。例如，在IIA 弦论中，我们知道存在稳定的空间维度是偶数的D膜，这是因为理论中存在相应的反对称规范场，这些反对称场的阶是奇数，等于对应的D膜的时空维度。可是，当我们在开弦微扰论中用边界条件来定义D膜时，边界条件本身的共形不变性与D膜的时空维数无关，从而，在IIA理论中我们可以定义空间维度是奇数的D膜。这些D膜由于不破坏开弦的共形不变的边界条件，所以是弦论中树图解。D膜的时空维度与超对称有关，空间维度是奇数的D膜在IIA理论中完全破坏超对称，所以不再是BPS态。同样，IIB弦论中存在空间维度是偶数的不稳定D膜。快子的质量平方是用弦的张力来量度的，所以快子的有效作用量应该包含弦激发态的效应。奇怪的是，快子的作用量可以有效地用一个推广的波恩－英费尔德形式来描写，这样弦激发态的效应似乎可以忽略。森假定当不稳定膜处于其最简单的状态时，快子的“真空”期待值是零，他证明，当快子期待值处于势能最低值时，不稳定膜完全消失。这样，快子可以用来有效地描述不稳定膜的衰变。因为快子本身带有势能，有人建议可以将快子看成早期宇宙暴涨过程中的暴涨子(inflaton)，驱动宇宙的暴涨过程。这是一个很有意思的建议，因为这个建议坚定在宇宙早期，可能存在膜和反膜的湮灭过程。可惜，快子作为暴涨子有一些理论上的困难，还没有完全被克服。快子的研究引出很多有趣的进展，如开弦可能是一种描述整个弦论的基本单元，闭弦以及D膜等等都可以用开弦理论来描述，这个猜测带来新一轮的弦场论的研究。玻色弦中的D膜是不稳定的，当存在许多D膜时，开弦的低能理论可以用快子的矩阵模型来研究，因为此时快子是一个矩阵。这个图象可以用来重新解释老矩阵模型，老矩阵模型是一个两维弦理论，其中矩阵的物理意义在80年代末并不清楚，只是弦世界面上三角剖分的一个对偶描述，现在的解释就很清楚了，矩阵模型其实是一种开弦理论，其矩阵变量是不稳定D0 膜上的快子。虽然这是开弦理论，在大N极限下，这个理论自动含有闭弦。

首页

热门◆

应用◆

游戏◆

欢迎新用户

消息

设置

会员

赞 (10) 分享

场论读了没一年，起码也有十个月了，感觉真的好久好久，当时刚刚去看场论的时候不算是从零开始也差不多了，因为场论需要的缘故去看张量、相对论、电动力学、黎曼几何、引力的东西，有些是提前学习，有些应该不在本科的范围内，也不知道怎么就这么过来了。回想起来应该是当时大二开始读的时候，头两章一方面觉得自己读得懂，另一方面的确有被吸引住，于是，于是。。。就入坑了。。。整本书反反复复翻了许多遍却从没有完整地啃下来，经常重头来过，所以一直也不敢说第一次的学习结束了，充其量就是第一次看的时间久了点。。直到上个月突破引力坍缩的瓶颈，觉得之后可以再找个几天时间把场论从头翻一遍想一遍就好了，终于有点希望曙光看到了。然后国庆回来直到今天结束，就特别激动，特想写一下，因为大概未来两年内没有时间机会再细读场论了。限于篇幅和自身的水平，在场论依旧还有很多不懂不通的地方，当然其实即便是觉得懂了也未必懂，只当留个纪念。一年来对相对论纸上谈兵的回顾总结，还有朗道场论里面特别不一样的，让我跪伏的地方。在当中，泡利的《相对论》对我的启发和帮助很大，特别我感觉两本书都十分注意围绕和突出物理定律的协变性，只是对引力部分的内容显得落后了。场论的确是一部天才之作，朗道对物理理论深刻的洞察，系统的表述，对语言的把握会让每一个人都羡慕吧。
相对性原理：所有自然定律在所有惯性参考系中都是相同的。不同的事件在四维时空（闵可夫斯基表述四维时空流形为世界）中间隔不变。结合相互作用传播速度无限大的假设称为伽利略相对性，参考系之间的坐标变换遵循伽利略变换，时间概念是绝对的，这样的参考系就被称为伽利略参考系。伽利略的相对性原理在过去成功之处为经典力学表现协变性，但麦克斯韦方程组在伽利略变换中表现为非协变性（在洛伦兹变换中两者却表现相反）。现在我们都知道相互作用传播不是瞬时的，应该存在最大相互作用传播速度，所以经典力学只是在低速情况足够精确。场论特别指出注意：最大传播速度的存在暗示着自然界中物体的运动速度不可能大于这个速度。这也好理解，后一时刻物体发生变动所传播的信号不会比前一时刻先到达，总是不违背因果性的；所以物体不能超光速运动；但伽利略相对性却是与此相违背的。
相对性原理结合相互作用传播速度的有限性称为爱因斯坦相对性，为满足间隔不变与麦克斯韦方程组的协变性，四维时空不是真欧几里得空间，而是基于更普遍的仿射空间的伪欧几里得空间——闵可夫斯基空间 [1]

，参考系之间的坐标变换遵循洛伦兹变换，数学上表示为四维时空轴之间的旋转变换（闵可夫斯基指出）。并且相对论中时间的概念不是绝对的：场论指出在绝对时间的基础上，由经典力学的速度合成法则获得在不同惯性参考系中的传播速度不同，就不存在相互作用的最大传播速度，与爱因斯坦相对性违背（迈克尔逊－莫雷实验也证明光速在不同惯性系和不同传播方向是相同的）。场论也特别指出相对论的速度合成的不对称与洛伦兹变换的非对易性。现在我们知道了相对性原理同相互作用的传播速度有限结合起来就是狭义相对论，即所有物理定律在洛伦兹变换下都具有协变性。
场论关于相对论力学部分篇幅不长却充满理论物理的简洁与和谐。第一性原理出发和先行的物理直觉，颠覆读者原有世界观的同时又将矛盾统一起来，特别在下面电磁场部分，特别体现理论物理的美——统一和对称。因为相对论力学同样满足最小作用量原理，并且作用量积分对于洛伦兹变换保持不变，故作用量必是一个标量函数和一阶微分；对于一个自由粒子，标量函数必是间隔，在过渡到经典力学确定准确形式，由此获得了相对论力学的拉格朗日函数。
第一次读场论的电磁场部分的时候就觉得这又是朗道卓尔不群的藐视其他物理书，原因有二吧。第一，场论的电磁场理论建立在四维空间和狭义相对论基础上。在场论的序言摘录就阐述了完整的、逻辑上严谨的验证电磁场理论本身就包含了狭义相对论。在四维视角的电磁场理论必涉及势和场的洛伦兹变换，有助于解释和理解场分解为电场和磁场只有相对意义 [2]

。场论的脉络就完全与一般的电动力学书相反，但不得不承认很成功。第二，基本计算都建立在张量分析基础上，在真欧式空间（包括复欧式空间）中矢量不需区分逆变矢量与协变矢量，但在闵可夫斯基空间中度规为-1的指标的上升或下降需要改变符号，因此做这样的区分就十分重要并且有必要，特别是在广义相对论中将引力几何化更是如此。从变换群的角度上说，我们必须区别函数行列式为+1的正常正交变换群和还包含有函数行列式为-1的更广泛的混合正交变换群 [3]

。洛伦兹群的不变式理论具有四维矢量和张量计算的形式。
在这儿就是让我觉得最惊艳的地方了：最小作用量原理推导麦克斯韦方程组。在推导运动方程的时候认为场是已知的，只变分粒子的轨道；那在给定电磁场中运动电荷的作用量由自由粒子作用量、粒子与场的相互作用量组成；前者在相对论力学已经知道全部内容，后者则必包括表征粒子的量和表征场的量。场的性质由四维势表征，在这里用势表征不但有数学上的方便，也更具有物理真实性 [4]

。在三维形式下分解四维势为标势和使矢势，获得了作用量形式，就知道了在给定电磁场中运动粒子的拉格朗日量和运动方程。实际上也就是第一对麦克斯韦方程组。在四维形式下使用最小作用量原理就获得了四维形式的电荷运动方程和电磁场张量，而电磁场张量是一反对称张量，电磁场的能量动量张量是一对称张量，形式对称，物理意义明显。在推导场方程，即第二对麦克斯韦方程组的时候，认为电荷运动已知的，只变分势；因为电磁场满足叠加原理，故场方程必是线性微分方程组，则作用量必是场的二次式构成的标量，形式就是电磁场张量的四维标量。对于电磁场来说知道麦克斯韦方程组就获得了相关的所有知识。而在辐射的内容中让我感到尤为不同的是在辐射中经常使用谱分解。
狭义相对论是基于相对性原理的，只对于惯性系物理规律成立，即只适用于惯性系。但爱因斯坦在1916年的长篇论文《广义相对论基础》中提出：“要用在所有坐标系中都成立的方程来表述自然的普遍定律，就是说，它对于任何变换都是协变的（广义协变）。”（在这里场论提出注意：具体的物理现象，包括物体运动的性质，在所有的参考系中是不同的）那么基于等效原理 [5]

以及从引力质量和惯性质量等同出发，将引力场几何化。由引力场变换到非惯性参考系等效的场，时空度规则决定曲线坐标系的所有几何特性，这个时空度规实际上就是黎曼度规。实际上通过黎曼几何，我们看到有引力存在（有物质存在）的空间存在一个非零的曲率张量，故而时空是弯曲的而不是平直的 [6]

；在引力场中的物体遵循测地线运动，测地线上矢量的协变导数为零，即测地线是引力场中的极值曲线。场论指出不可能用任何坐标变换使决定其度规的量在整个时空都化为伽利略坐标的值，这样的时空称为弯曲时空（将黎曼度规的十个独立各量通过坐标变换到伽利略坐标的值一般是做不到的）而这在平直空间中是可以做到的。通过变分引力场的作用量与物质的作用量就获得了爱因斯坦方程（引力场方程），方程的左边是代表空间曲率的曲率项，方程右边是物质的能量动量张量。方程的系数由近似情况下牛顿的引力理论确定，但爱因斯坦的引力理论得到不一样的结果，比如讨论引力势我们知道在史瓦西场运动的粒子，只要能量足够大就会坠落在引力源。在中心对称情形下求解爱因斯坦引力场方程这一非线性方程，我们在史瓦西球上获得引力坍缩和黑洞的相关内容。场论里关于引力的内容感觉下来就是也具有朗道风格，但好像没怎么特别感觉到那种对全书系统的把握，可能是后面增补的缘故，也是因为引力的确十分抽象，不懂不通之处也大多在此。而据我所知，做引力的人也真的很少很少，不过今年据说发现了原初引力波的证据，如果证实又是广义相对论理论的一大成功之处啊。
甲午年九月十一
云霄于家中展书重翻场论回顾怀念留
[1]

.仿射空间中非对角元为0，对角元为的度规空间称为欧式空间；度规所有对角元具有相同符号称为真欧式空间，同时具有不同符号称为伪欧式空间；度规中三个对角元有相同符号，另一个具有不同符号称为闵可夫斯基空间。
[2]

.电场或磁场在某一惯性系不存在，却同时在另一惯性系存在；或是在某一惯性系运动的磁铁引起感应现象，在另一惯性系导体运动产生感生电流。
[3]

.在泡利的相对论中首次看到这个概念，更详尽的内容参考了Jackson的经典电动力学，下册第11章11.7洛伦兹变换的矩阵表示；无穷小生成元（1980年12月印刷），其中称为正常洛伦兹变换、非正常洛伦兹变换；前者相当于连续施以恒等变换，后者在空间反演和时间反演中取不同符号。但在场论中并不重要。
[4]