自旋为1/2的粒子是什么形状的，三维真的有转两圈才能和自己重合的形状？
这个问题是不是说明了粒子内部是更高维度的空间？
按票数排序按时间排序
14 个回答
关键词：基本群，投影表示，周期边界条件。
要完整回答这个问题，涉及到的数学概念比较多。
首先，我们描述旋转，是用”旋转群“的概念，即群SO(3)。同时感兴趣的是这个群的李代数so(3)，即量子力学里的角动量代数。
群和代数提供了两个角度切入这个问题：
1. 从群的角度。
首先，如果我们把旋转操作不看作一个群作用，而是一系列无穷小操作的组合，即转一圈相当于N次旋转(180/N)°，以示与”不转“的区别。这样，一个旋转就变成了群流形上的一条线(contour)，任何回到原位（群单位元）的旋转体现为群流形上的一个圈(loop)。然后我们去看被转的对象：我们做以下识别(distinguish)，即两个不同的旋转操作，对于任意对象而言，必然等同的条件是，它们所代表的contour之间同伦（这一结论适用于任意群）。对于转圈，则是它们所代表的loop同伦。”不转“即一个收缩至一点的loop，那么和”不转“等同的”转圈“，就必须能够（在群流形上）收缩至一点。如果假设群的实现是可微的，那么这样的识别是逻辑上可能的最细致的识别。
量子态可以做这种识别，因为它可以有内部自由度（比如相位）。经典态无法做这么细致的识别，因为它的自由度是固定的。
问题来了：SO(3)群的拓扑性质（形状）很特殊，是一个对径认同的球体，它上面有两类不等价的loop，其中一类等价于点（”不转“），而另一类和它并不等价，而”转一圈“这个操作就属于这个非平凡的类里面。简单来说，”转一圈“这个操作无法连续得变化为”不转“的操作（你可以试一试）。
数学上，这称为”SO(3)群的基本群是
”。
这有什么意义呢？当我们在量子理论中实现一个群操作时，允许这样的事情发生：
即群的表示
并不完全同构于群
本身。这称为投影表示。这有点像一个
-orbifold。在SO(3)的情况下，这就是个-orbifold，其定轴旋转的子流形就是一个莫比乌斯带（的边界） @杨晓堃 。
2. 从代数的角度。
这个角度就比较常见了，一般的量子力学书都是这么讲的。首先，so(3)=su(2)，即两个群的李代数相同。然后，我们把这个代数称为角动量代数，并且写出它的所有表示。然后我们发现有自旋1/2的表示。这样的表示对于轨道角动量不适用的原因是波函数在实空间的单值性，导致了周期边界条件；而自旋角动量适用恰恰是因为它的旋转并不对应实空间的点，所以不需要有单值性，因此可以有反周期(anti-periodic)边界条件。
当然，这造成了很多人（比如题主）的困惑。简单把它归结于“自旋是内秉性质”不是一个很有说服力的方法，因为它其实还是来自于空间旋转。
两者的联系：
拥有相同的李代数的群SO(3)和SU(2)，后者有着简单拓扑
，而前者恰好是后者的某种automorphism的商集，过程中改变了拓扑，而这种automorphism则成了前者的基本群。因此，前者算上投影表示就和后者完全相同了。
经 @flying zz 提醒，更好的说法是：拓扑上，SU(2)是SO(3)的universal cover，所以它们有相同的李代数但不同的拓扑，而且前者的所有表示和后者的所有投影表示完全相同。对于一般的群，应该也有如此性质。比如高维旋转群，Spin(n)就定义为SO(n)的universal cover。这就是为什么我们可以省略介绍投影表示，而直接使用群SU(2)=Spin(3)作为量子理论的旋转群，并给出多一倍的表示。 显示全部
要完整回答这个问题，涉及到的数学概念比较多。
首先，我们描述旋转，是用”旋转群“的概念，即群SO(3)。同时感兴趣的是这个群的李代数so(3)，即量子力学里的角动量代数。
群和代数提供了两个角度切入这个问题：
1. 从群的角度。
首先，如果我们把旋转操作不看作一个群作用，而是一系列无穷小操作的组合，即转一圈相当于N次旋转(180/N)°，以示与”不转“的区别。这样，一个旋转就变成了群流形上的一条线(contour)，任何回到原位（群单位元）的旋转体现为群流形上的一个圈(loop)。然后我们去看被转的对象：我们做以下识别(distinguish)，即两个不同的旋转操作，对于任意对象而言，必然等同的条件是，它们所代表的contour之间同伦（这一结论适用于任意群）。对于转圈，则是它们所代表的loop同伦。”不转“即一个收缩至一点的loop，那么和”不转“等同的”转圈“，就必须能够（在群流形上）收缩至一点。如果假设群的实现是可微的，那么这样的识别是逻辑上可能的最细致的识别。
量子态可以做这种识别，因为它可以有内部自由度（比如相位）。经典态无法做这么细致的识别，因为它的自由度是固定的。
问题来了：SO(3)群的拓扑性质（形状）很特殊，是一个对径认同的球体，它上面有两类不等价的loop，其中一类等价于点（”不转“），而另一类和它并不等价，而”转一圈“这个操作就属于这个非平凡的类里面。简单来说，”转一圈“这个操作无法连续得变化为”不转“的操作（你可以试一试）。
数学上，这称为”SO(3)群的基本群是
这有什么意义呢？当我们在量子理论中实现一个群操作时，允许这样的事情发生：
即群的表示
2. 从代数的角度。
这个角度就比较常见了，一般的量子力学书都是这么讲的。首先，so(3)=su(2)，即两个群的李代数相同。然后，我们把这个代数称为角动量代数，并且写出它的所有表示。然后我们发现有自旋1/2的表示。这样的表示对于轨道角动量不适用的原因是波函数在实空间的单值性，导致了周期边界条件；而自旋角动量适用恰恰是因为它的旋转并不对应实空间的点，所以不需要有单值性，因此可以有反周期(anti-periodic)边界条件。
当然，这造成了很多人（比如题主）的困惑。简单把它归结于“自旋是内秉性质”不是一个很有说服力的方法，因为它其实还是来自于空间旋转。
两者的联系：
拥有相同的李代数的群SO(3)和SU(2)，后者有着简单拓扑
经 @flying zz 提醒，更好的说法是：拓扑上，SU(2)是SO(3)的universal cover，所以它们有相同的李代数但不同的拓扑，而且前者的所有表示和后者的所有投影表示完全相同。对于一般的群，应该也有如此性质。比如高维旋转群，Spin(n)就定义为SO(n)的universal cover。这就是为什么我们可以省略介绍投影表示，而直接使用群SU(2)=Spin(3)作为量子理论的旋转群，并给出多一倍的表示。 显示全部
首先，自旋是内禀自由度，与外部三维实空间的角动量不同，前者对应角动量量子数为半整数，而后者则为整数。简而言之，所谓转两圈重合是指1/2自旋粒子本征态的变量θ、φ至少需要改变4π才能使波函数复原，而θ、φ就是自旋本征矢在球坐标系下的方向角，所以可以形象地描述为需要转两圈才能与自身重合。至于内部空间的维度，自旋1/2的粒子有两个本征态，任何一个态可以是二者的复系数线性叠加，二维复空间加上归一化条件，因此是三维实空间。
科幻可以随便看，科普就不要看《时间简史》了。顺便说一个例子，或许不太准确，莫比乌斯带好像也可以看成是转两圈才能回到原点。
科幻可以随便看，科普就不要看《时间简史》了。顺便说一个例子，或许不太准确，莫比乌斯带好像也可以看成是转两圈才能回到原点。
有好多从群论出发的代数理解方式。我个人比较喜欢几何一点的方式，所以，“黎曼面”是一个非常不错的概念，去理解群论中的同构同态等概念时非常有帮助。
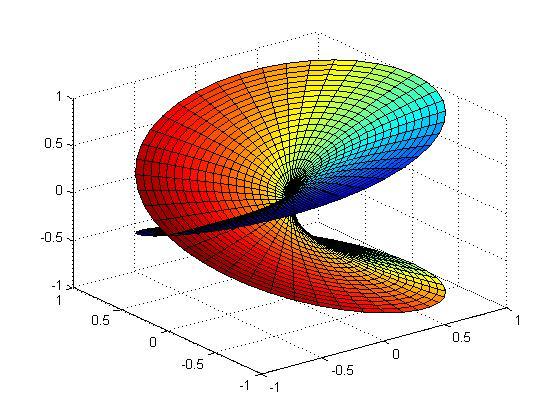上图是一个
的黎曼面，引自wiki。这个例子非常适合于自旋1/2，对于其他的自旋，可以找到其他的黎曼面来说明。
这个奇怪的曲面，自己和自己交叉了，原因是我们需要在三维表现它。。简而言之，这个奇怪的曲面才是自旋1/2的粒子在转动时所经历的空间，这个粒子转动一圈，从黎曼面的上页转到了下页，对于粒子来说这是两个不同的地方，其性质表现得不一样是很正常的，只有转两圈才能回去。
自旋实际上是粒子的内禀自由度，我们很难从宏观角度直接体会。但是实验就是这么告诉我们的，粒子有自旋。
上图是一个这个奇怪的曲面，自己和自己交叉了，原因是我们需要在三维表现它。。简而言之，这个奇怪的曲面才是自旋1/2的粒子在转动时所经历的空间，这个粒子转动一圈，从黎曼面的上页转到了下页，对于粒子来说这是两个不同的地方，其性质表现得不一样是很正常的，只有转两圈才能回去。
自旋实际上是粒子的内禀自由度，我们很难从宏观角度直接体会。但是实验就是这么告诉我们的，粒子有自旋。
要从纤维丛的角度去理解。
1. 场的时空坐标在闵科夫斯基时空中，场的取值在纤维里面。
2. 在闵科夫斯基时空中，对称性由洛伦兹群Lo描述。
3. 在物理学理论中，要保持这个对称性，即洛伦兹群的作用。所以，洛伦兹群在纤维里面，会有一个表示，这个表示就是SL(2,C)。
4. 在闵科夫斯基时空中，对于转动来说（就是我们常见的转动）由SO(3)给出。这个对称性在纤维里面，要由SU(2)来描述。两者之间有个关系，你会发现，SO(3)下，转动了\theta角度，转换到纤维里面，就变成了在SU(2)下转动了\theta/2。两者差一个1/2.
（这就是你想问的转两圈才重合的问题。实际上，是闵科夫斯基时空中转了一圈，纤维里面转了两圈。数学上，管这个叫做two-fold covering space）。
1. 场的时空坐标在闵科夫斯基时空中，场的取值在纤维里面。
2. 在闵科夫斯基时空中，对称性由洛伦兹群Lo描述。
3. 在物理学理论中，要保持这个对称性，即洛伦兹群的作用。所以，洛伦兹群在纤维里面，会有一个表示，这个表示就是SL(2,C)。
4. 在闵科夫斯基时空中，对于转动来说（就是我们常见的转动）由SO(3)给出。这个对称性在纤维里面，要由SU(2)来描述。两者之间有个关系，你会发现，SO(3)下，转动了\theta角度，转换到纤维里面，就变成了在SU(2)下转动了\theta/2。两者差一个1/2.
（这就是你想问的转两圈才重合的问题。实际上，是闵科夫斯基时空中转了一圈，纤维里面转了两圈。数学上，管这个叫做two-fold covering space）。
是不是跟高维有关系，我不清楚…但是有一点我是清楚的，题主所说的“转两圈与本身重合”表明你在用宏观的视角去理解自旋，而自旋是纯粹的量子力学概念，因此这样的理解方式是不对的。量子力学里面的自旋是没有宏观物理量与之对应的。
我记得Dirac在阐述他的方程时说过一段话，意思是他在列方程时甚至没有借鉴自旋的概念，而自旋则是求解Dirac方程自然而然得到的结果。（原话找不到了…）
还有一个，宏观的旋转会有特定的旋转轴，而自旋则与坐标系的选择没有关系，一个电子在一个分子体系中，无论你如何建立坐标系求解这个电子的方程，其自旋永远都是1/2，坐标系有可能改变的仅仅是其在极轴的分量…
量子力学半吊子，可能有不妥的地方，求轻拍…
我记得Dirac在阐述他的方程时说过一段话，意思是他在列方程时甚至没有借鉴自旋的概念，而自旋则是求解Dirac方程自然而然得到的结果。（原话找不到了…）
还有一个，宏观的旋转会有特定的旋转轴，而自旋则与坐标系的选择没有关系，一个电子在一个分子体系中，无论你如何建立坐标系求解这个电子的方程，其自旋永远都是1/2，坐标系有可能改变的仅仅是其在极轴的分量…
量子力学半吊子，可能有不妥的地方，求轻拍…
自旋为1/2的粒子是什么形状的，三维真的有转两圈才能和自己重合的形状？不一定，还有可能粒子被连在一根绸带上。如图所示（或动态 Spinor orientation entanglement animated ）：
这个问题是不是说明了粒子内部是更高维度的空间？
转360度不能回到原来的位型：
转720度就可以：
动态图片： Belt trick
教学视频：http://vimeo.com/62228139 、http://vimeo.com/62143283
这根绸带看不见摸不着，唯一的作用就是你旋转粒子的时候隔硬你。
附：
Feynman 演示自旋1/2粒子的绸带论证：https://www.youtube.com/watch?v=cKzzG5DS6V8&feature=youtu.be
狄拉克理论，自旋是相对论效应导致的。
不要问我为什么自旋，这是人为的模型。
其实我们很无奈，语言描述来自生活，生活是经典的，上帝为什么偏偏让我们用经典的语言来描述微观世界？
经典模型能够解释上帝吗？
我不知道。
不要问我为什么自旋，这是人为的模型。
其实我们很无奈，语言描述来自生活，生活是经典的，上帝为什么偏偏让我们用经典的语言来描述微观世界？
经典模型能够解释上帝吗？
我不知道。
Schottenloher intro to conformal field theory写中心扩张那章比较初等易读，有几个具体的例子比如su2这个。
-------
我觉得谈论形状没什么意义。
在量子力学里面讨论系统的对称性其实更方便的是从无穷小的角度（数学上也就是Lie group的线性化----Lie algebra）去做计算，比如这里的旋转群SO(3)，但因为是从无穷小的层面出发（local），得到的整体性质最natural的应该是没有拓扑障碍（这时就像第一个回答所说的，可以把投影表示lift为线性表示，在做lifting的时候实际上我们考虑的是SU(2)被U(1)做中心扩张后的线性表示，但对su(2)的例子，其中心扩张是trivial的）的群，也就是SO(3)的通用覆盖SU(2)。
为什么要从无穷下的角度出发，一个可能的解释是对于更一般的情况例如CFT，其conformal symmetry的“对称群”，2D conformal group实际上并不是一个well defined的group（有一个结论是无法从W代数和V代数构建一个Lie group），所以我们直接考虑其无穷小变换Witt algebra的u(1)中心扩张也就是Virasoro algebra的表示。
-------
我觉得谈论形状没什么意义。
在量子力学里面讨论系统的对称性其实更方便的是从无穷小的角度（数学上也就是Lie group的线性化----Lie algebra）去做计算，比如这里的旋转群SO(3)，但因为是从无穷小的层面出发（local），得到的整体性质最natural的应该是没有拓扑障碍（这时就像第一个回答所说的，可以把投影表示lift为线性表示，在做lifting的时候实际上我们考虑的是SU(2)被U(1)做中心扩张后的线性表示，但对su(2)的例子，其中心扩张是trivial的）的群，也就是SO(3)的通用覆盖SU(2)。
为什么要从无穷下的角度出发，一个可能的解释是对于更一般的情况例如CFT，其conformal symmetry的“对称群”，2D conformal group实际上并不是一个well defined的group（有一个结论是无法从W代数和V代数构建一个Lie group），所以我们直接考虑其无穷小变换Witt algebra的u(1)中心扩张也就是Virasoro algebra的表示。
知乎用户
收起
如果稍微延伸一下，比如考察一下石墨烯中的pseudo spin ,也许可以有更直观的理解。其波函数有两个分量，每个分量的相位对应于倒空间中的波矢k(相对于Dirac 点)。其形式上和真正的spin很象，即相位是要增加4pi 才回到原状态。这对应什么事实呢？即题主所说的这个态要在k空间绕两圈才能封闭(即回到原态)。这个有pseudo spin的态,反映了所在的k空间的拓扑性质，即此二维的k空间不是简单的曲面，而是有奇点的，即Dirac点。所以此态绕Dirac 点一圈不能回到原态，换言之做封闭曲线积分不为零。这也即是复变函数里的留数定理所说的，闭合曲面里存在奇点。如果没有奇点，积分为零，波函数获得相位2pi,回到原态。事实上，环绕一圈后此态获得相位Pi，所谓berry phase, 反映的就是k空间在Dirac 点附近的拓扑性质。正是此有奇点的空间性质造成的berry phase，造成比如特殊的量子霍尔平台等等啥的。而回到原问题，这个「粒子」什么样子的？只能说你把它投影到实空间看吧，实际上波函数在实空间中分布在两套格点上(石墨烯晶格为复格子，有两套不等价格点).所以可以想象这个所谓「粒子」并不是一个实空间中的一个很局域像波包一样的东西。
很多回答的都太高深，用了各种场论和群论的理论。理论首先是用来描述客观现实规律的，然后这一规律有了发展和预测。至于高维空间是理论的发展和描述，有些是解释和想象，帮助理解的。所以还是回到自旋概念的产生和客观现实上来。物理是依托于实验的。所以从实验上理解最简单。
自旋的提出是因为电子在磁场中观测到新的能级分裂。量子力学的能级是离散的，薛定谔方程的解也就是现实从在的能量数值要符合整数条件，就有量子数的概念。而磁场下这个能级分裂的自旋量子数和实验符合的正好1/2。.从宏观上想，如果电子自己旋转就会和磁场有相互作用，所以这个能级分裂的量子数就命名为自旋了。至于是实际是如何，没有什么直接的观测来证实。尺度太小。
自旋的提出是因为电子在磁场中观测到新的能级分裂。量子力学的能级是离散的，薛定谔方程的解也就是现实从在的能量数值要符合整数条件，就有量子数的概念。而磁场下这个能级分裂的自旋量子数和实验符合的正好1/2。.从宏观上想，如果电子自己旋转就会和磁场有相互作用，所以这个能级分裂的量子数就命名为自旋了。至于是实际是如何，没有什么直接的观测来证实。尺度太小。
No comments:
Post a Comment